地浸“水平井注-直井抽”井场流场数值模拟与井网优化

2021-03-01李召坤周根茂常江芳赵利信刘佳佳

铀矿冶 2021年1期

李召坤，周根茂，李坡，常江芳，杨睿，赵利信，刘佳佳

(1.中核矿业科技集团有限公司，北京 101149；2.石家庄铁道大学，河北石家庄 050043)

目前地浸矿山开发主要利用直井作为抽注液井。随着铀矿地质勘查“攻深找盲”工作的推进，在中国部分地区相继发现了一批低渗透、大埋深砂岩铀矿资源[1-2]。常规直井开采此类资源面临着井网稠密、单井控矿面积小、成本高等制约因素。与常规直井相比，水平井技术具有过流面积大、浸出死角小等优势，可大幅提高注液量，降低注液井施工成本[3-8]。

目前对“水平井注-直井抽”地浸井场渗流特点研究较少。为此，利用ANASYS数值模拟软件建立数值模型，以最大化浸出范围为依据，优选“水平井注-直井抽”的井网参数。

1 数值模拟控制方程

进行的数值模拟研究基于ANASYS多孔介质模型[9]。ANASYS多孔介质模型可以适用于较均质的地层渗流模拟工作。多孔介质模型就是定义一个多孔介质区域，设定该区域的孔隙度和流体的黏性阻力系数和惯性阻力系数。理论上讲，是在动量方程的右侧增加了一个动量源项[10]。除常规流体力学控制方程外，本次模拟还用到以下控制方程。

1.1 基于表观速度的多孔介质动量方程

对于单相介质和多相介质，多孔介质模型可以使用表观速度或物理速度形式的公式。多孔介质模型通过在动量方程中增加源项，来模拟计算区域中多孔性材料对流体的流动阻力。据ANASYS使用手册，该源项由两部分组成，即Darcy黏性阻力项和惯性损失项：

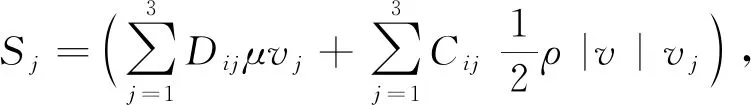
(1)

式中：Dij和Cij分别为黏性阻力和惯性损失系数矩阵；μ为黏性系数；ρ为流体密度；vj为流体在j方向的速度分量。这个负的动量源项(Sj)导致多孔介质单元中的压力降。

1.2 达西黏性阻力项

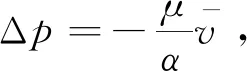
(2)

式中：1/αij为系数矩阵Dij的项；Δni为多孔介质在3个坐标方向上的厚度。

1.3 惯性损失项

当速度比较高，或模拟多孔板和管排时，有时可忽略渗透阻力项，只保留惯性阻力项，则多孔介质方程(1)简化为

(3)

或写成3个坐标方向上的压力降：

(4)

式中：C2ij为系数矩阵C中的项；Δni为多孔介质在3个坐标方向上的厚度。

2 模型建立

“水平井注-直井抽”是参照五点型布井方式，用水平注液井代替了竖直注液井。因井场几何结构规律性较好，取一个代表单元进行模拟。

2.1 二维模型建立

二维水平面模型长为100 m，宽为100 m，水平井与竖井直径均为0.1 m，网格质量均达到0.7以上，如图1所示。边界条件分别设置为inlet、outlet、wall、porous-jump及symmetry。

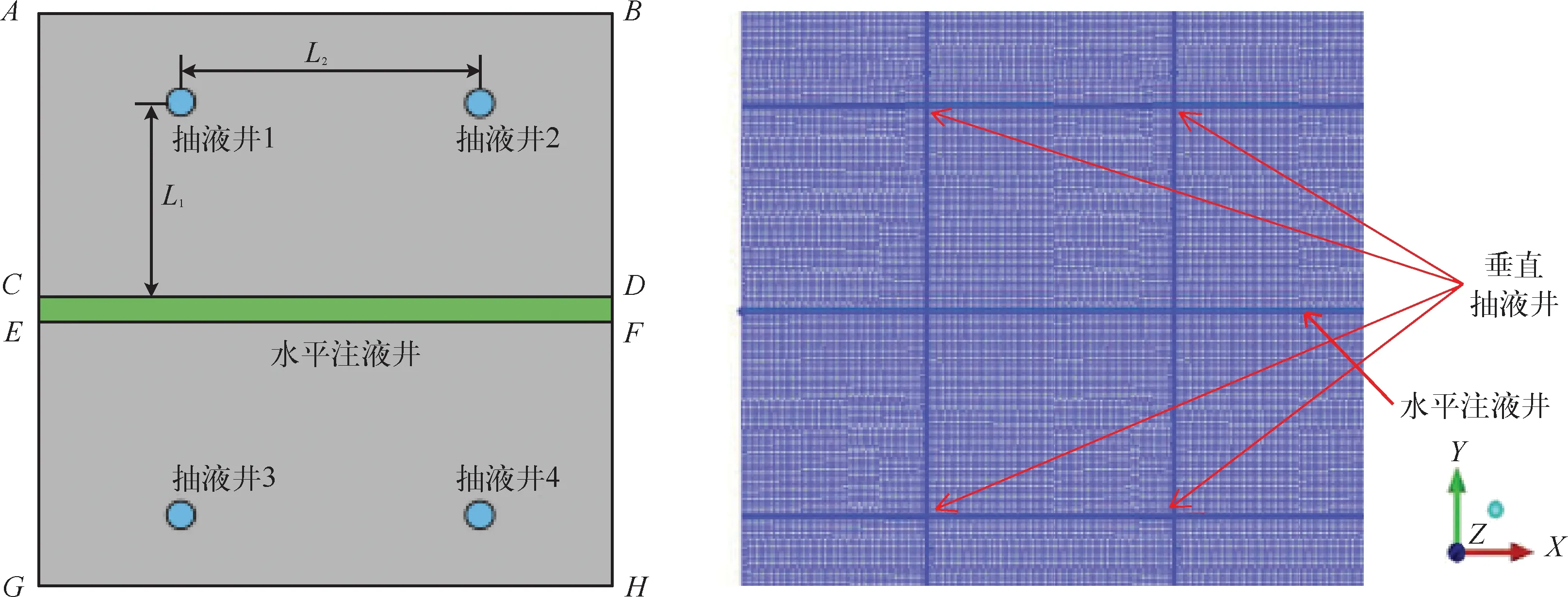
图1 二维水平剖面数值模型示意图

图1中由CDFE围成的区域为水平井水平段，ABDC和EFHG围成的区域为矿层(多孔介质区)，1、2、3、4为竖直抽液井。建模时设置研究区边界AB=AG=100 m。其中，抽液井和水平注液井之间的垂直距离为L1，两口抽液井之间的间距为L2。为了优化注抽井的布置，本研究设置了4个方案，见表1。

表1 二维水平剖面数值模拟方案

为了确定水平井在含矿含水层中距离上下矿层边界的位置，建立了竖直剖面的二维模型，如图2所示。为了能够同时包含2个竖井，横向剖面模型尺寸设宽为70 m，含矿含水层厚度为20 m，水平井及竖井直径均为0.1 m，网格质量保证均在0.7以上。为了提高数值模拟精度，对近井地带网格进行局部加密处理[11]。数值模拟方案见表2。

2.2 三维模型建立

三维模型尺寸为长200 m、宽200 m、高20 m，水平井及竖井的直径均为0.1 m。由于模型尺寸过大，将其切分为四部分，取四分之一进行计算。模型分为压力入口、压力出口、不透水边界、对称边界及跳跃边界等5个边界条件，模型网格数量为3.2×105个，网格质量均在0.5以上，如图3所示。模型完成后，通过数值模拟对不同方案进行分析，来确定最佳方案。

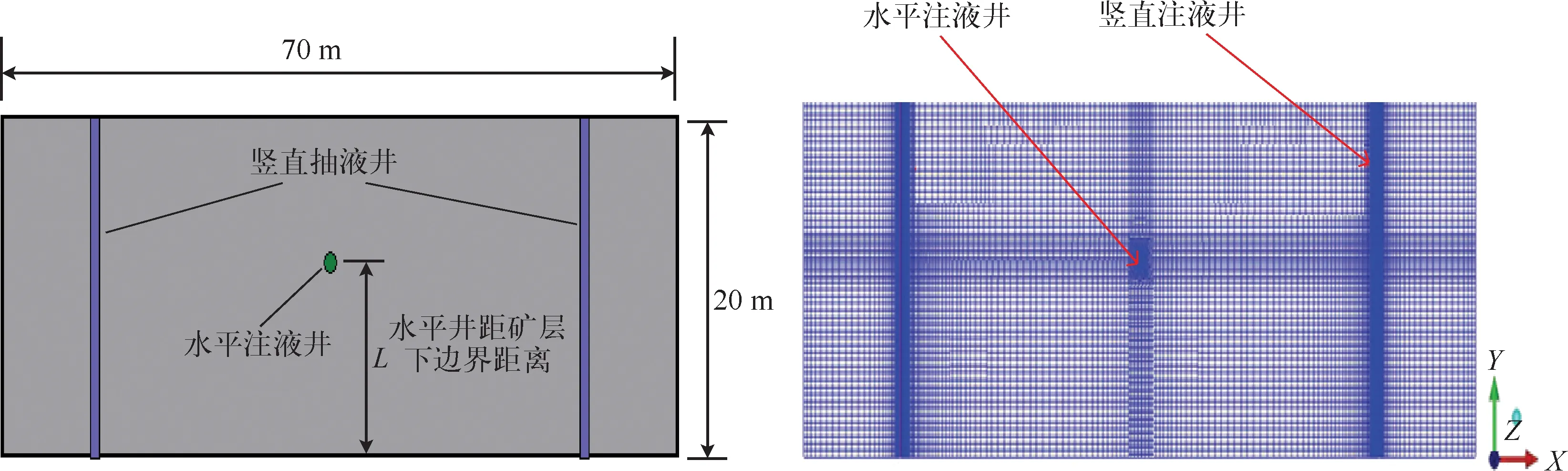
图2 二维竖直剖面数值模型示意图

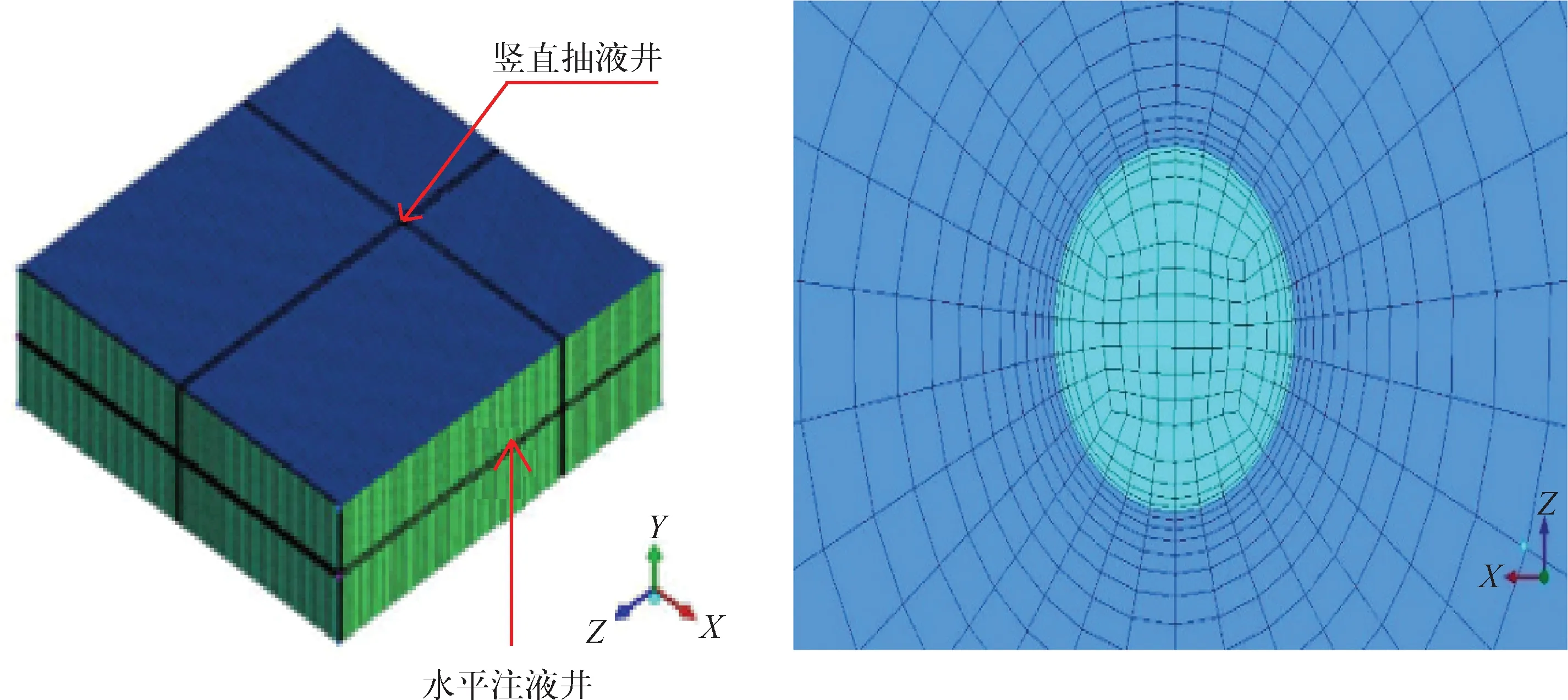
图3 三维模型和局部O-Grid网格图

表2 二维竖直剖面数值模拟方案

由于模型较大，需对局部位置进行加密。考虑到井孔附近渗流规律的特殊性，对井孔附近建立O-Grid网格来消除网格畸变，避免计算时产生较大的误差。竖直抽井与水平井的间距为L1，竖直抽井间的间距为L2。数值模拟方案见表3。

计算参数孔隙率取30%，水头差取80 m，矿层的渗透系数取0.4 m/d。溶浸液为含CO2、O2的混合溶液。水平注液井设置为压力入口，抽液井设置为压力出口，出口压力为大气压。

表3 三维数值模拟方案

3 二维数值模拟结果分析

3.1 水平剖面流场特点分析

地浸溶浸剂主要是含O2和CO2的混合水溶液，从CE和DF入口进入水平井中，再通过水平井壁上的割缝渗入周围矿层。在一定压力下，CO2溶于水中产生碳酸，假定碳酸在注液井内液体中的质量分数为30%(将碳酸视为示踪剂，显示溶浸液的渗透范围)。现采取控制变量法，取相同时间t=(1.2e+6) s时，对比不同方案的渗流情况。

当t=0 s时，因入口处还没有溶浸液流过，碳酸浓度为0。开始计算后，水平井内溶浸液的流速及整体流场内的压强分布迅速达到稳定状态。水平井内的溶浸液首先由两端入口流入，随后向水平井中部流动，两股溶浸液在水平井中部相遇后，优势流通道逐渐被堵塞，溶浸液开始通过水平井井壁上的孔隙向周围的岩石渗流，t=(1.2e+6)s时的具体分布如图4所示。

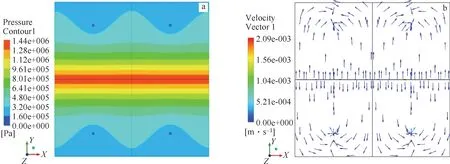
图4 流场速度矢量图和压力云图

从图4(a)可看出，在水平井近井地带，地层流场前缘为一条近似平行于水平井的直线，形成了线性驱替的效果。与常规五点型或七点型井场近纺锤体的流场分布相比，这样的流场可以有效减少浸出死角，达到均匀驱替的效果。

从图4(b)可看出，近水平井地带渗流均匀，出现浸出死角的概率较小。但是在两口竖直抽液井连线中点处，由于渗流压差较小，不论是流速还是溶液浓度都较小，容易形成浸出死角。为此选择观察点A(图5)，观测点坐标为(50，80)，以该点的碳酸质量分数变化特点优选参数，其浓度变化如图6所示。

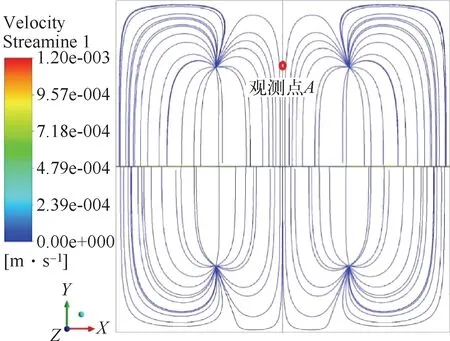
图5 观测点A位置示意图

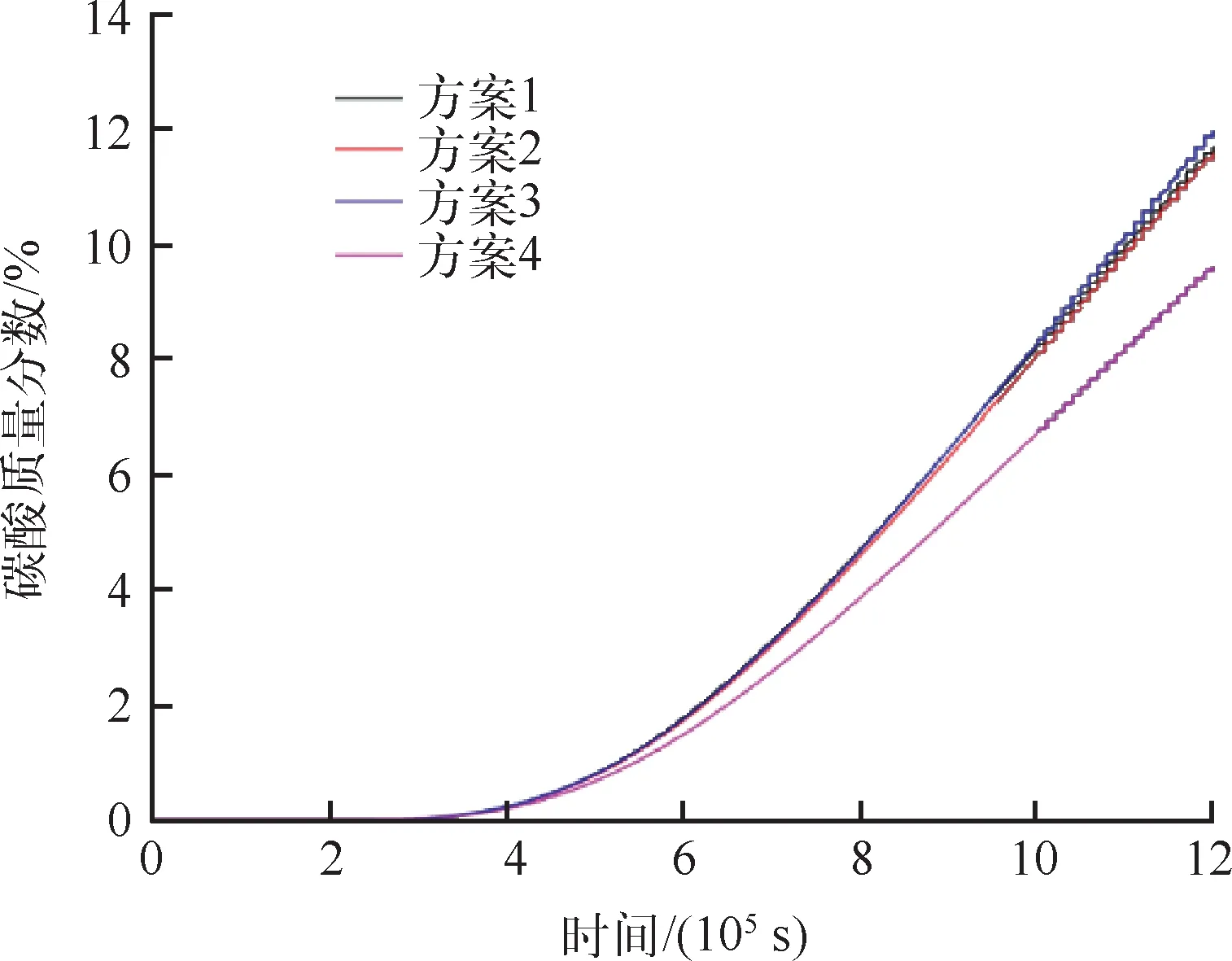
图6 观测点碳酸质量分数变化曲线

从图6可看出，不同方案条件下，该点溶液浓度都是从3×105s开始出现，说明溶液到达该点的速度基本一致；但是在后期，方案3的增长率略大于其他3个方案。因此从平面渗流的角度来看，方案3与其他方案相比最优，即L1=35 m，L2=50 m。

3.2 竖直剖面流场特点分析

在水平井水平剖面的模拟中已经定出水平井和竖直抽井的最优间距，可以根据横向剖面的模拟进一步优化水平井在矿层中的深度，确定最优的布井位置。

矿层上下两端除抽液井口外，均设置为不透水边界，两侧设置为自由边界，不同方案条件下的流场如图7所示。可以看出，流场随着水平井位置的变化而产生变化，水平井距离上下矿层较近时，流线疏密差异较大，流速分布不均匀，不稳定，不利于溶浸液的均匀推进，同时也最容易产生渗流死角。通过数值模拟比较几种方案可以发现，溶液自重对流场的影响较小。其中，方案Ⅱ当水平井位于矿层中间位置时，流速分布最为均匀和稳定，是较为理想的状态。

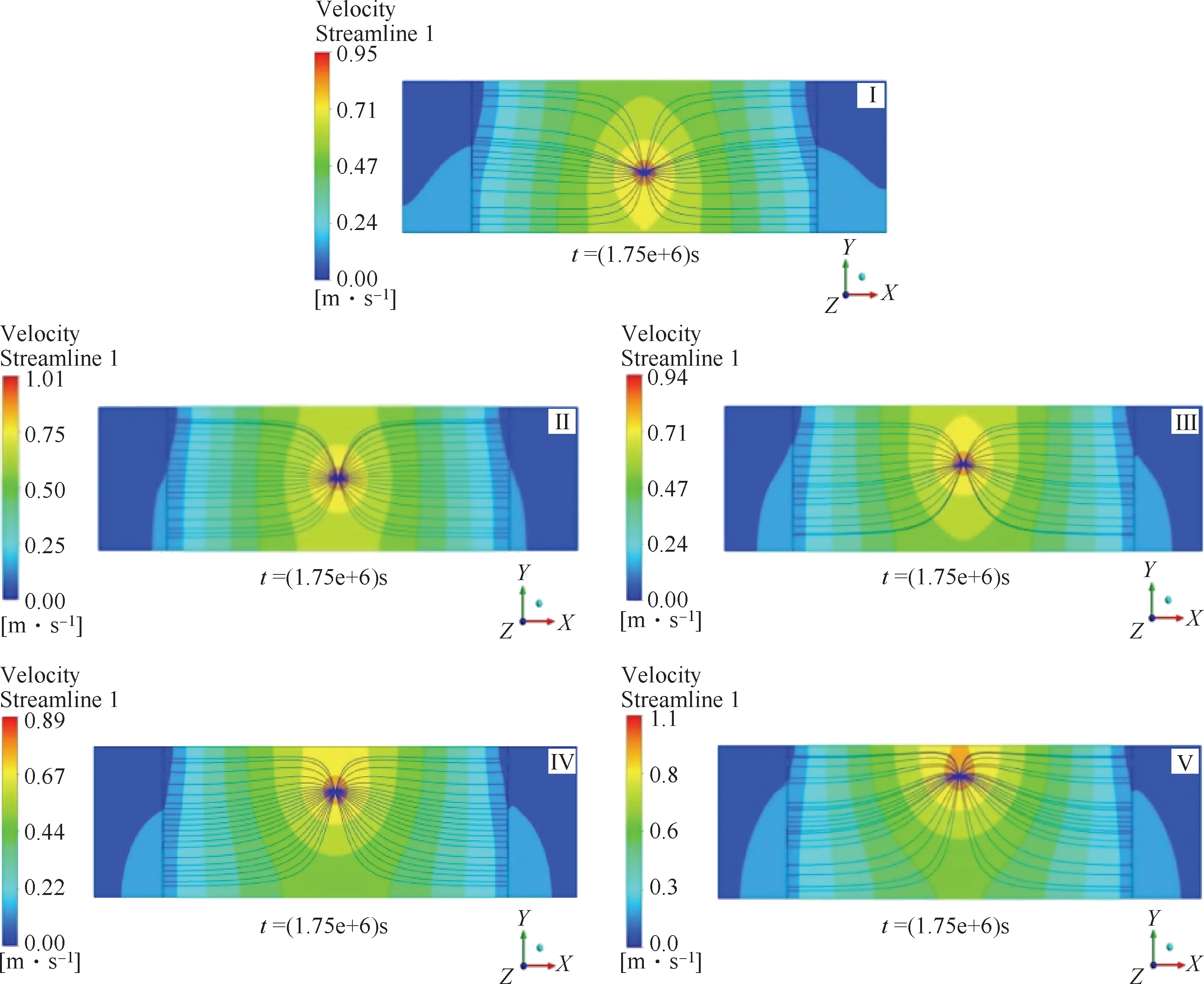
图7 不同方案条件下流场图

浓度是判断渗流效果是否为最优的最佳依据，可根据不同方案时相同浓度部分所占面积百分比，来判定方案是否为最优。模拟中，以溶浸液中碳酸浓度大于其初始浓度50%的渗流面积百分比为标准进行判别，方案Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ的溶浸液中碳酸浓度大于其初始浓度50%的渗流面积分别为470.71、475.23、471.93、447.22、392.10 m2，各方案的渗流面积百分比如图8所示。

从图8可看出，方案Ⅱ溶浸液中碳酸浓度大于其初始浓度50%的渗流面积为475.23 m2，相应渗流面积百分比为33.95%，此时浸出死角最小。因此，当水平井距矿层下边界10 m，即水平井位于含矿含水层中间位置时渗流效果最好。

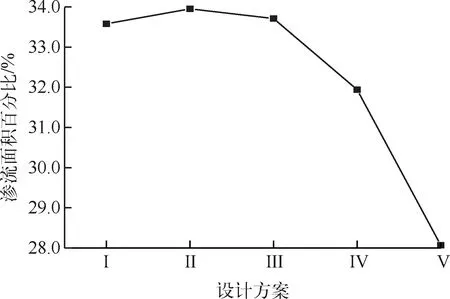
图8 溶浸液中碳酸浓度大于其初始浓度50%的渗流面积百分比

4 三维数值模拟结果分析

三维数值模拟可以得到不同浸出时间里溶液的渗流体积分数。设溶浸液中碳酸浓度大于其初始浓度50%的部分为当前有效浸出范围，溶浸液中碳酸浓度小于其初始浓度10%的部分为当前浸出死角。利用软件的数据后处理功能，可以得到表4的模拟结果。

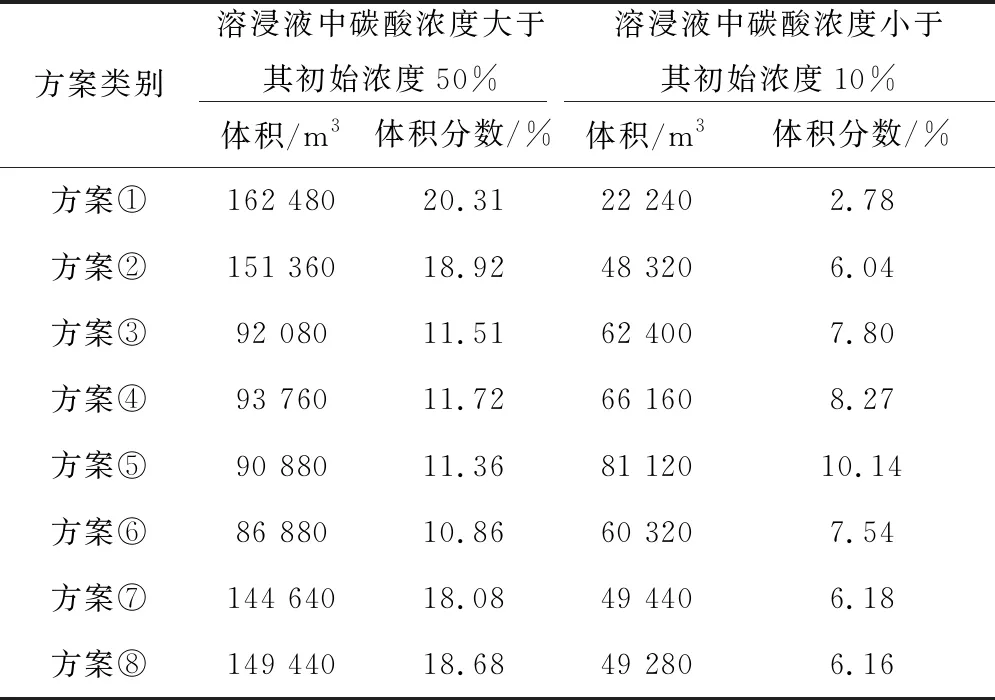
表4 三维数值模拟结果

从表4可看出，方案①、②、⑦、⑧效果较好，方案③、④、⑤、⑥效果较差，说明渗流效果受L1和L2共同作用。对比方案③、④、⑤，可以发现三者差距不大，这说明在L2(即竖直抽液井的间距)一定时，水平井与竖直抽液井之间的距离在一定时间内对浸出范围影响较小。总的来说，在考虑提高有效浸出范围且减小浸出死角的前提下，方案①为最优方案，即直井与水平井的间距L1为35 m，直井与直井的间距L2为50 m。