多喷管运载火箭底部热环境研究

闫指江，沈 丹，吴彦森，蒲鹏宇，宫宇昆

（1. 北京宇航系统工程研究所，北京，100076；2. 北京理工大学，北京，100081）

0 引 言

为了获得更大的推力，运载火箭动力系统常采用多喷管并联方案，如美国的土星V火箭[1]、苏联的能源号火箭、欧空局的阿里安-5火箭、日本的H-ⅡA火箭以及中国的CZ-2F火箭等[2]。在运载火箭上升的过程中，相邻喷管射流之间、射流与自由来流之间相互作用，在火箭底部形成复杂的循环流动或冲击反流，使运载火箭底部承受较高的热载荷[3]。因此，在运载火箭总体设计的过程中，需要预估底部热流并采取相应的热防护措施。然而，由于运载火箭底部流动极为复杂，理论分析方法与实际的遥测结果相比偏差较大；同时，由于缩比效应以及测量的不确定性，试验数据难以直接用于底部热流的预估[3,4]。因此，有必要建立相应的数值模型对火箭底部热环境进行仿真分析，明确底部流动结构以及各种因素对底部热流的影响，最终为底部热防护设计提供参考。

Hideyo等[5]采用密度基隐式求解器求解耦合了realizablek-ε湍流模型[6]的N-S方程，同时采用P-1辐射模型[7]求解辐射传热，得出了H-ⅡA火箭包含喷管射流在内的流场以及底部壁面热流分布。Mehta等[8]采用SST-kω与BSL-kω（Baseline）湍流模型对Musial等[9]所做的四喷管火箭缩比模型风洞试验进行了数值计算，分析对比了四喷管火箭底部热环境对不同数值模型的灵敏度。Patel等[10]在此基础上采用BSL湍流模型对两喷管构型的Antares运载火箭底部热环境进行了数值计算，并考虑了燃气回流后在底部区域的复燃。乔野、聂万胜等[11]对火箭模型进行了简化，仅考虑火箭尾端及喷管部分，采用耦合了Realizablek-ε湍流模型的N-S方程描述尾焰流动过程，考虑复燃反应的影响，得到不同飞行高度下火箭动力系统的尾焰流场结构。

目前为止，国内外对芯级为两喷管构型并捆绑助推器的运载火箭底部热环境的分析研究还较少，且缺少对火箭侧壁面边界层流动分离规律的研究。本文以芯级两喷管加四助推器火箭为研究对象，对其周围流场域进行了网格划分，采用密度基隐式求解器对耦合了SST湍流模型的N-S方程进行求解，拟得出火箭底部热环境特性，为运载火箭底部热防护设计提供参考。

1 物理模型和计算方法

1.1 物理模型

几何模型如图1所示，由直径为3.35 m的芯级火箭和4个直径为2.25 m的助推器组成，4个助推器按旋转90°分布。芯级火箭底部装有2台发动机，每台发动机喷管向外偏转2°；每个助推器底部装有1台发动机，发动机喷管向外偏转6°。

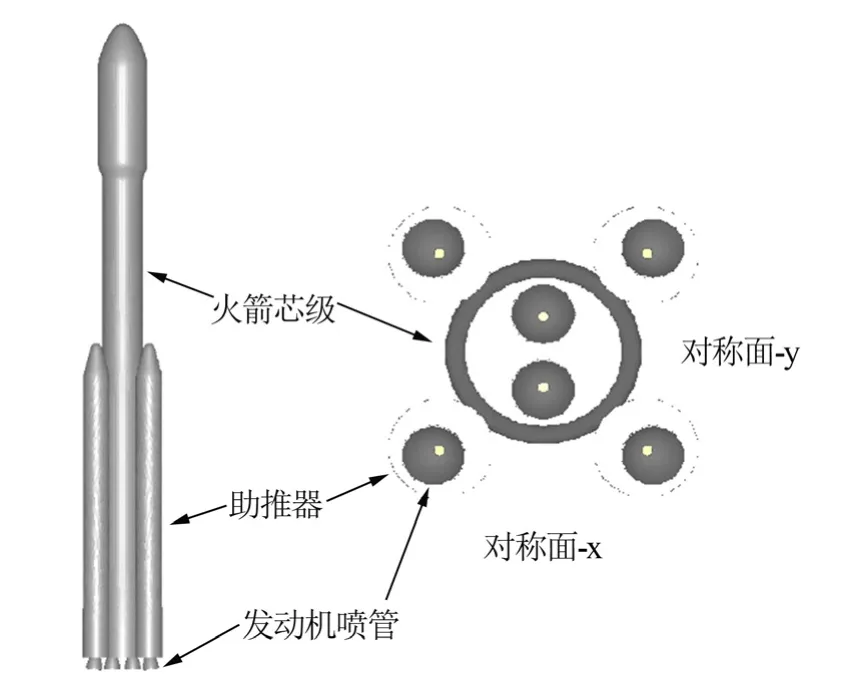
图1 多喷管火箭的几何模型Fig.1 Geometric Model of the Multi-nozzle Rocket

本文研究的运载火箭发动机为液氧/煤油型，喷管出口燃气比热比为1.16，喉部与出口面积比为1∶35，喉部直径约为200 mm。液氧/煤油发动机性能参数如表1所示，其中，Tinlet与Pinlet分别为推力室总温与总压；Cp与μ为推力室燃气定压比热与动力粘性系数。

表1 火箭发动机性能参数Tab.1 Parameters of Rocket Engine Performance

1.2 计算模型

根据文献[8]的计算经验，采用SST模型[12]与BSL模型所得出的底部热流数据相差小于2%，而SST模型能够更好地反应逆压梯度下的流动分离现象，因此本文选取SST湍流模型用于仿真计算。同时，根据文献[8]的结果，采用等效燃气与空气双组份混合模型计算得出的热流比采用多组分有限速率化学反应模型计算结果更高，从工程安全要求与提高计算效率综合考虑，采用双组分混合气体模型计算是合理的。

1.3 控制方程求解

控制方程采用时间推进的隐式方法求解，该方法具有较强的稳定性。应用有限体积法离散喷管内部和火箭周围流场控制方程，对流项采用二阶迎风格式、扩散项采用中心差分格式构建差分方程，梯度采用基于单元中心的最小二乘法获得，采用Roe格式[13]对单元面上的通量进行离散，最终采用Gauss-Seidel迭代结合代数多重网格方法[14]对离散后的代数方程组进行求解。

1.4 网格划分与边界条件

根据几何模型的对称性，选取1/4模型以提高计算效率。为了便于局部网格加密，采用非结构四面体网格对边界层外流场区域进行网格划分。为了准确模拟运载火箭的底部流动结构，在底部区域进行了网格加密。为了模拟火箭侧壁面流动分离，准确计算火箭壁面热流，采用棱柱网格解析边界层内流动，确保第一层网格中心处计算网格与边界条件如图2所示，网格总量为570万。不同飞行高度对应边界条件设置如表2所示，其中，Ma∞、p∞、T∞分别代表来流马赫数、静压与静温，10.5 km与26 km为低海拔工况，45 km与62 km为高海拔工况。除喷管内壁面与喷管边缘为绝热壁面外，其余壁面均保持恒温330 K。

图2 网格模型和边界条件Fig.2 Mesh and Boundary Conditions

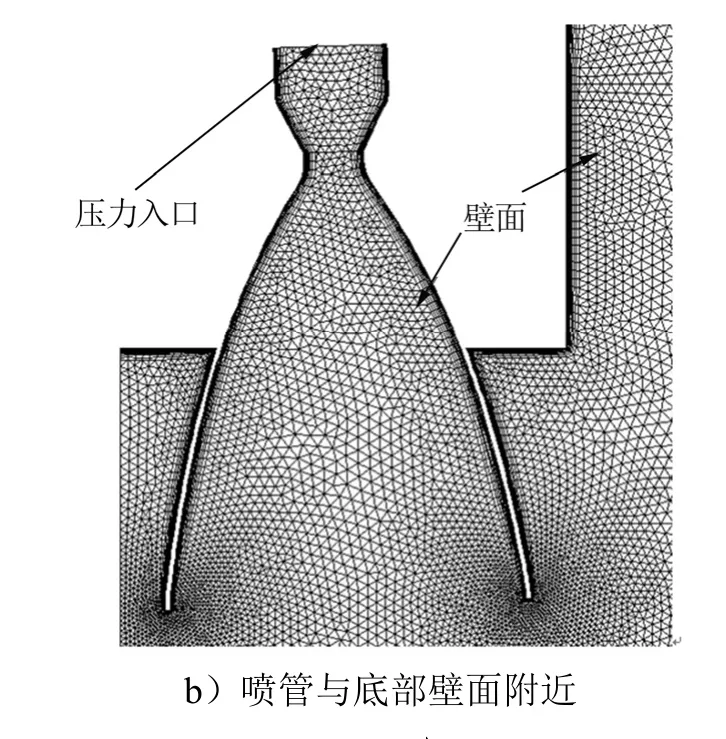
续图2

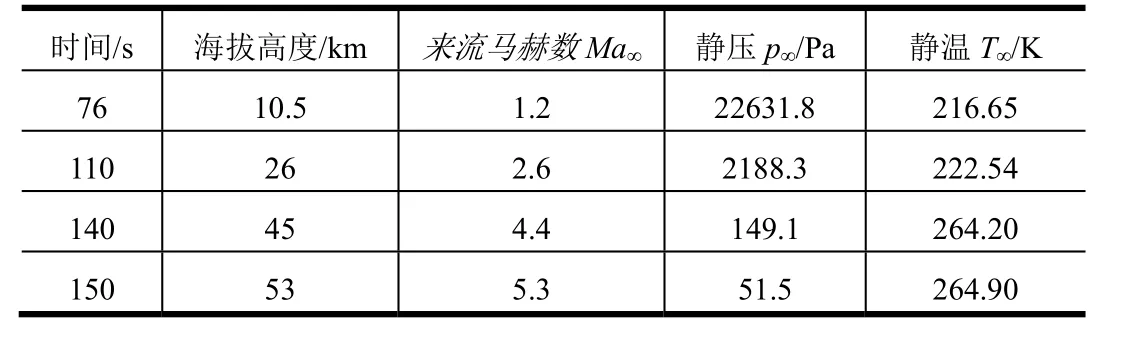
表2 边界条件选用参数Tab.2 Boundary Conditions Selection Parameters

1.5 计算方法验证

为了验证数值计算方法的有效性，选取文献[8]中用于对比验证的四喷管火箭缩比试验工况[9]进行数值仿真计算。该试验将四喷管火箭缩比模型安装在风洞中模拟真实来流条件下火箭发动机稳定工作过程，通过传感器测量火箭模型底盘上的热流密度分布。图3显示了选取的试验工况下数值计算结果与试验数据的对比。由图3可知，二者反映的热流密度沿底部半径的分布规律具有较高的一致性，说明选取的数值计算方法能够较好地反映多喷管运载火箭底部热环境特性。

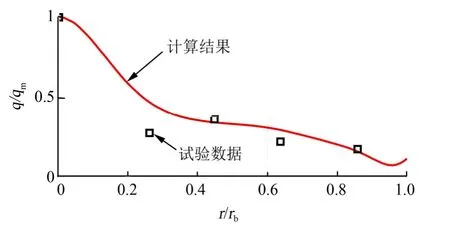
图3 底部热流延径向分布对比Fig.3 Comparison of Base Heat Flux Distribution

2 计算结果分析

运载火箭底部流动受其整体几何外形的影响。图4为不同飞行高度下火箭周围流场马赫数云图。如图4a所示，在飞行高度较低时，来流马赫数较低，箭体对来流的阻挡效应不明显。随着飞行高度升高，来流马赫数增大，在箭体头部形成弓形激波，波后流速降低，压强与温度升高，从而与远场来流条件产生差异，进而影响底部流动。由图4d可知，高海拔工况下火箭底部上游出现亚声速区，此时底部流动与上游来流相互影响，故箭体外形对底部流动的影响不可忽略。因此，保留全箭模型进行仿真计算对于准确反映火箭底部流动是必要的。此外，相比芯级头部，助推器头部距底部更近，因此其产生的激波能够更为直接地干扰尾焰流场，对底部流动的影响更大。

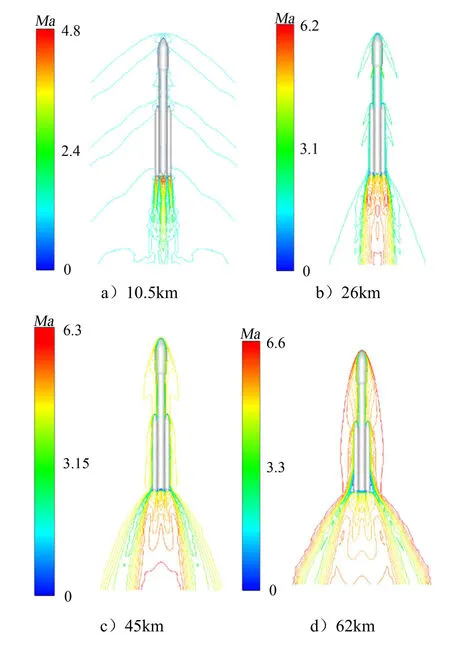
图4 尾焰流场马赫数云图Fig.4 Wake Flow Field Mach Contour

尾焰射流膨胀角决定了火箭底部流动结构，进而影响底部壁面热流分布。由图4可知，随着飞行高度的升高，环境压强降低，燃气射流逐渐从过膨胀状态发展为高度欠膨胀状态[15]。

不同飞行高度下火箭底部流动矢量如图5所示。低海拔工况下，射流膨胀角较小，射流间碰撞较弱，而来流动压较大，此时射流混合边界层内一部分动量较小的燃气相互碰撞后向底部流动，在来流的剪切作用下形成循环流动，在一定高度范围内随着飞行高度升高，底部冲击区逐渐从中心向外移动；而在高海拔工况下，射流膨胀剧烈，来流动压较低，因此相邻喷管射流碰撞后直接从碰撞点反向冲击火箭底部，并阻挡动压较低的来流空气流入底部区域。此时冲击区集中在底部中心处。从火箭底部近壁面流场温度可以看出，高海拔工况底部近壁面流场温度高于3000 K，远高于低海拔工况，说明高海拔工况下火箭底部的流热环境更为恶劣。

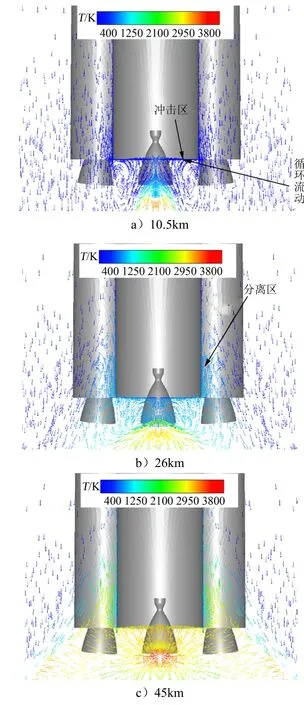
图5 流动矢量的温度云图Fig.5 Flow Vectors Colored by Temperature

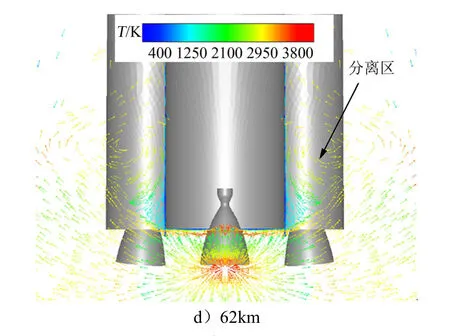
续图5

芯级火箭底部热流密度分布随飞行高度的变化如图6所示，图中热流峰值区位置与图5中的冲击区对应，热流峰值大小取决于高温气体冲击强度，即气流密度与冲击速度。低海拔工况下，高温气体对底部的冲击强度较低。随着飞行高度升高，热流峰值区从底部中心向边缘移动，热流逐渐升高。而高海拔工况下高温气体冲击强度较高，峰值大小为低海拔工况的2～10倍，热流峰值区集中在底部中心。相比于45 km工况，62 km高度下底部热流密度峰值有所下降，这是由于62 km工况下环境压强较低，底部高温冲击气流更为稀薄，使得高温气体冲击强度下降，从而降低了底部热流密度。

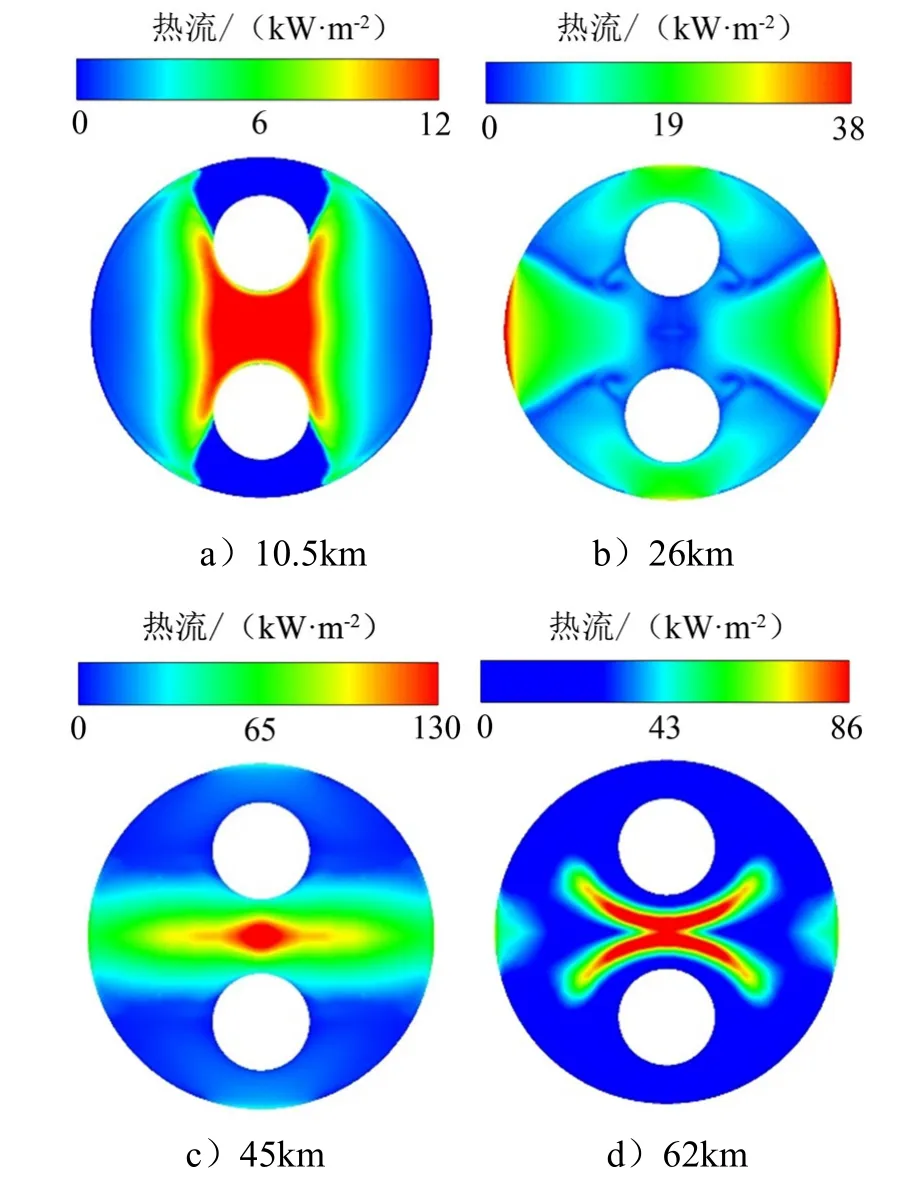
图6 底部壁面热流分布Fig.6 Bottom Wall Heat Flux

除增大底部热流外，射流膨胀角增大还会强化其对来流的阻挡作用，使其上游侧壁面产生流动分离。由图5可知，随着尾焰射流对来流的阻挡逐渐增强，飞行高度达到26 km时火箭侧壁面已出现流动分离，分离临界高度应位于10.5～26 km之间。流动分离的存在使底部燃气向上流动填充分离区，加热火箭侧壁面。

由于助推器的阻挡作用，火箭芯级侧壁面流动分离主要分布在相邻助推器之间的区域。定义穿过芯级两喷管的对称面为x面，穿过两喷管之间区域的对称面为y面，分别获取两对称面内火箭侧壁面流动分离点距火箭底面的高度，如表3所示。在同一工况下，y对称面内分离点位置更高，这是由于在y对称面内芯级两股喷管射流相互碰撞，相比于只有单股射流的x对称面，其对上游来流的阻挡作用更强，产生的逆压梯度更大，因而分离点更高。对不同飞行高度，分离点位置随飞行高度升高逐渐上移，这与尾焰射流对来流的阻挡作用随飞行高度升高而增强是一致的。火箭芯级侧壁面热流密度分布如图7所示，流动分离区内的高温气体显著增大了火箭侧壁面热流。

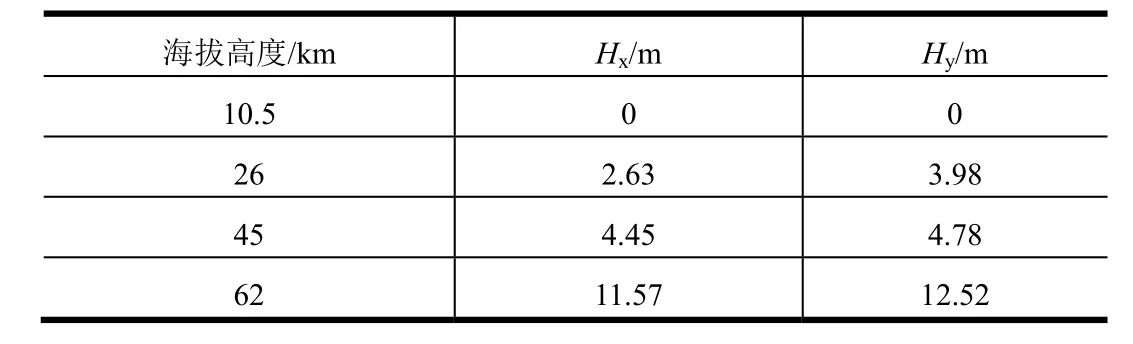
表3 箭体侧壁不同位置Tab.3 Different Positions on the Side Wall of the Body

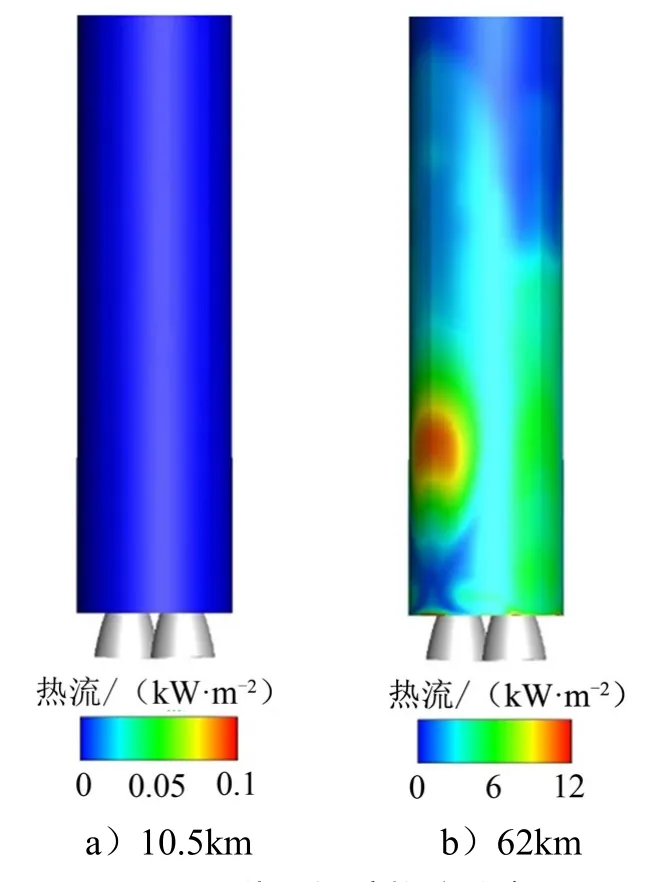
图7 芯级侧壁热流分布Fig.7 Heat Flux on the Lateral Wall

3 结 论

本文建立了两喷管芯级加四助推器火箭底部热环境的数值计算模型，分别研究了10.5 km、26 km、45 km、62 km 4种工况下火箭底部热环境特性，并分析了火箭侧壁面的流动分离现象及其对壁面热流的影响，得出了如下结论：

a）火箭头部激波使得波后流动速度降低，增大波后温度与压强，从而影响火箭底部流动。相比于芯级头部，助推器对底部流场影响更大。

b）火箭底部热流主要由高温气体对底部的冲击强度决定，随着飞行高度升高，射流膨胀角增大，高温燃气对底部的冲击增强，使得底部热流密度峰值逐渐增大，在一定高度范围内峰值区从底部中心向外移动，之后又回到底部中心区域。因此底部热流随飞行高度升高先增大后减小，45 km高度下底部热流最大。

c）尾焰燃气射流对来流的阻挡作用会导致箭体侧壁面边界层发生流动分离，临界分离高度在10.5～26 km之间。流动分离使得高温燃气加热箭体侧壁面，其中热流密度最大点位于侧壁面底部边缘处。侧壁热流大小以及流动分离点高度取决于尾焰射流对来流的阻挡作用，射流阻挡作用越强，分离点越高，侧壁热流密度峰值和加热范围越大。