多层热防护结构烧蚀传热模型研究

丁 晨，牛智玲，单亦姣，张子骏，王 尧

（中国运载火箭技术研究院，北京，100076）

0 引 言

航天飞行器在大气层内长时间高速飞行时，飞行器表面与大气剧烈摩擦，形成了对飞行器严重的气动加热与气流剪切力，可能导致结构性能下降、设备功能失效，影响飞行器可靠性与安全性，甚至导致飞行失利。目前，飞行器热防护系统广泛采用烧蚀材料作为主要防热材料，即通过热分解、熔融、蒸发、升华等方式牺牲部分材料以换取积极的防热效果[1]，其中，硅基防热材料是一种常用的熔化型烧蚀防热材料，由树脂与二氧化硅（SiO2）纤维为主要成分复合而成，因其具有导热系数低、成型工艺简单、抗烧蚀性能和隔热性能好等优点，大量应用于航天飞行器热防护[2]。

防热材料烧蚀过程存在树脂热解、热解气体引射、SiO2纤维熔化等复杂过程，是影响防热性能的重要因素。姜贵庆等[3]将SiO2熔融物的流动近似为定常可压缩层流流动，建立了硅基防热材料稳态烧蚀速率计算方法。高贺等[4]通过求解液态层控制方程计算烧蚀速率与液态层流动速度的表达式。时圣波[5]研究了高硅氧/酚醛复合材料烧蚀环境下的质量损失机理及吸热机理，基于表面烧蚀理论和气体边界层理论，提出了防热材料表面烧蚀性能预示方法。进一步考虑热解气体的流动与传热，有学者提出了热解气体与多孔碳化层传热模型[6]。

为适应新型导弹日益严酷的气动热环境，同时实现导弹减重目标，近年来，研究人员提出了使用非均质防热材料进行热防护的方案，并研究了防热材料热响应计算方法。蒋凌澜等[7]采用分层法将功能梯度防热材料平面结构划分成若干层，提出了梯度型防热材料烧蚀/温度场计算方法，研究发现，梯度型防热材料能明显减少向内部结构传导的热量，减轻防热结构的重量。马忠辉等[8]分析了多层隔热结构导热与辐射复合换热问题，建立了多层隔热结构瞬态传热分析模型。柴峻[9]建立了不考虑烧蚀的多层隔热结构传热模型，得出增加隔热层厚度能显著提高隔热效果。

多层热防护结构由防热层、隔热层、承力结构组成，相比于常规热防护结构，能够适应更为复杂的气动力热环境，同时，由于隔热层材料隔热性能好，密度较轻，能够显著降低防热结构重量。本文建立了多层热防护结构烧蚀模型与变厚度材料传热模型，研究了多层热防护结构传热特性，分析了防热层厚度对温度响应特性的影响，为多层热防护结构设计优化提供参考。

1 防热材料烧蚀模型

防热材料在气动加热与气流剪切力作用下，SiO2纤维逐渐融化形成流动的液态层。液态层在防热材料表面流动满足简化的边界层方程，控制方程如下：

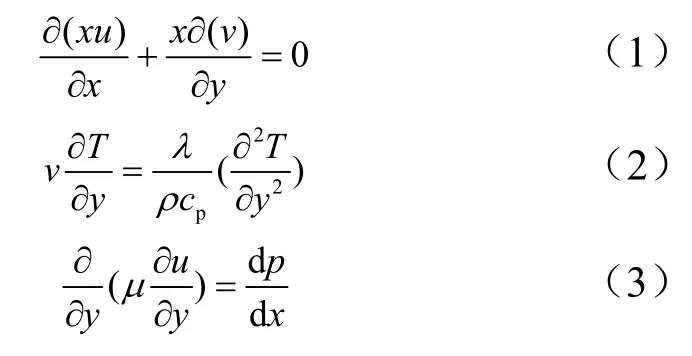
式中x轴沿烧蚀平面并指向气流流动方向；y轴垂直于烧蚀平面并指向烧蚀材料外侧；x为沿物面的坐标；u为沿物面的切向速度；v为垂直于物面的法向速度；ρ为熔融物密度；μ为熔融物动力粘性系数；p为物面压强；T为熔融物温度；λ为熔融物导热系数；cp为熔融物比热容。

烧蚀表面（y=0）满足：

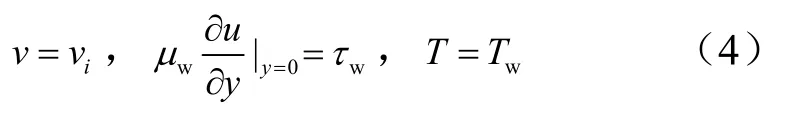
式中Tw为外壁面温度；vi为汽化烧蚀速率；τw为壁面气动剪切力，考虑粘性系数与温度成指数关系，即其中a与b为常数，由熔融物粘性系数随温度变化关系拟合而来。

烧蚀层与原始材料界面处（y=-∞）满足：

式中v-∞为烧蚀速率；T0为材料初始温度。对式（2）与式（3）进行积分运算后，代入式（1），可得烧蚀速率v-∞表达式：

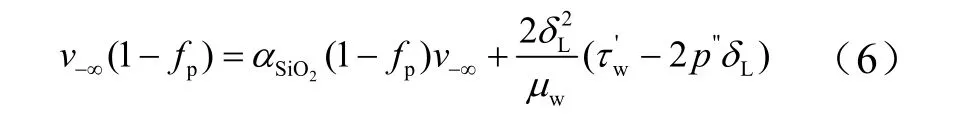
式中fp为树脂质量分数；τw'为壁面剪切梯度；δL为液态层厚度；为压力沿x方向二阶导数，为驻点压力，p∞为来流空气压力，R0为烧蚀体曲率半径；αSiO2为SiO2的蒸发质量分数，根据气-液交界面上组元质量守恒，假设传热系数与传质系数相等，可得：

式中hre为来流空气恢复焓；φ为质量引射因子，其值的大小表示未被阻塞的热流密度的百分数，经验关系式为[5]

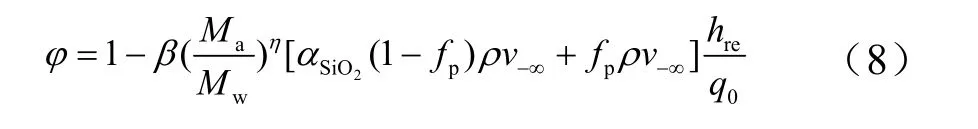
式中β与η取值为：对层流β=0.62，η=0.26；对湍流β=0.2，η=0.33。Ma为空气的摩尔质量；Mw为壁面混合气体的平均摩尔质量；q0为热壁热流；CSiO2为SiO2蒸气浓度，与蒸汽压pv的关系为

式中ep为壁面附近气动压力；Mv为SiO2摩尔质量。

进入壁面的热流包括考虑了阻塞效应的气动加热热流φq0、碳的燃烧反应放热吸热机理包括材料对外界的辐射热流εσTw4、烧蚀质量的热容吸热树脂热解吸热SiO2蒸发吸热以及进入材料内部的净热流。由于硅基材料具有较低的热传导系数，绝大部分的气动热被烧蚀过程消耗，本文不考虑进入材料内部净热流的影响。因此，烧蚀体表面的能量守恒方程可表示为

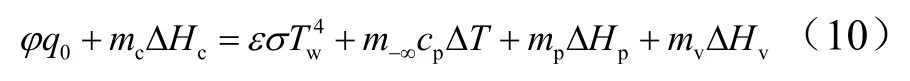
式中m-∞为总烧蚀质量损失，ΔT为烧蚀表面温度变化，mp为树脂热解反应质量损失，为SiO2蒸发质量损失率，，其中，Mc为碳元素的相对分子质量，CO2为边界层外缘氧的质量浓度，MO为氧元素的相对分子质量；cm为碳的氧化反应质量损失率，

求解式（6）与式（10），可以得出外界气动热条件下烧蚀速率v-∞与烧蚀壁面温度wT。

高硅氧/酚醛复合材料的基本参数按表1选取，需要说明的是，由于烧蚀过程中材料温度与组分不断变化，材料密度与比热容不断变化。

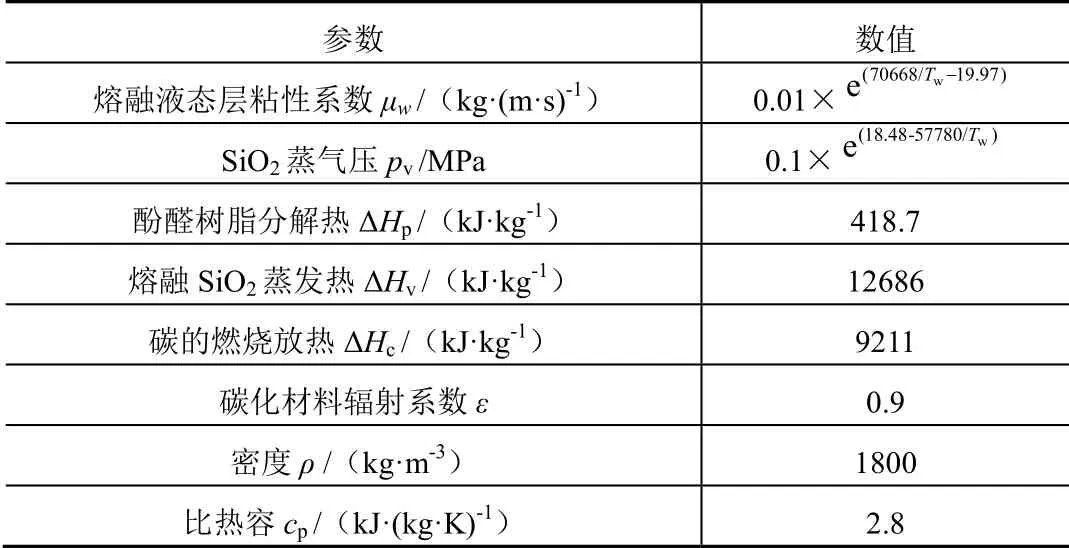
表1 高硅氧/酚醛复合材料基本参数Tab.1 Thermal Properties of Silica/Phenolic Composite

按本文计算方法得出的烧蚀速率结果和文献[10]中电弧风洞试验值对比如表2所示，表中qcold为冷壁热流，其与热壁热流q0的关系为从表2中可以看出，不同冷壁热流以及来流恢复焓条件下，本文计算结果与实验结果最大误差为9.4%，计算结果和试验值吻合较好，验证了烧蚀模型的正确性。

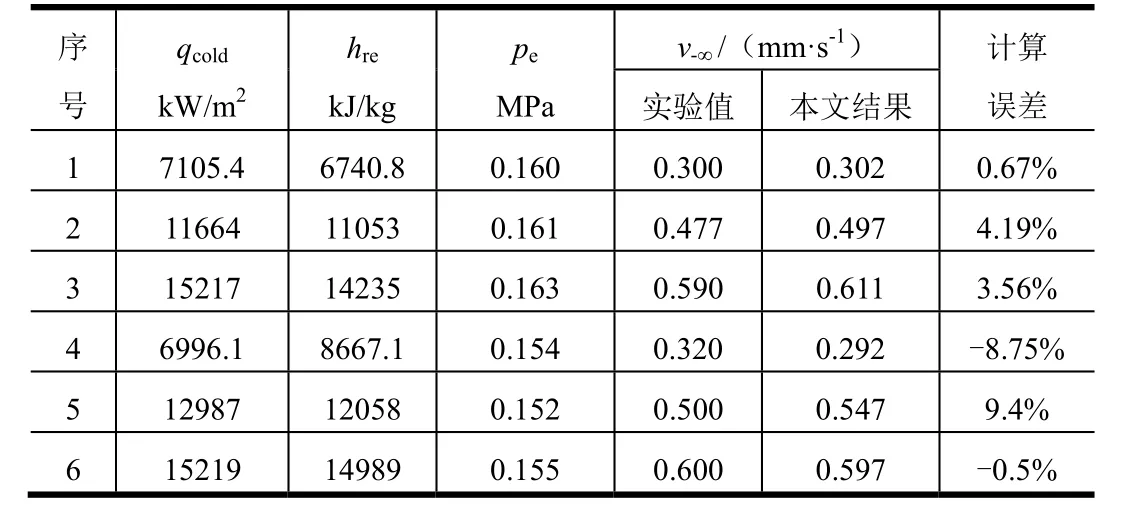
表2 电弧加热器热环境下烧蚀速率计算结果与试验值的比较Tab.2 Comparisons of Ablation Rate Between Arc Tunnel Experimental Results and Calculation Data

2 多层热防护结构传热模型

多层热防护结构如图1所示。防热层采用传统防热材料，用于承受气流剪切力，并通过烧蚀过程吸收气动热，为隔热层提供耐受范围内的温度环境，隔热层采用软木等低密度材料，阻隔气动热向承力结构的传递。

图1 多层热防护结构示意Fig.1 Schemetic of Multi-layer Thermal Protection System

导弹热防护结构大面积传热为一维导热过程，将多层防热结构区域离散化，定义节点如图2所示，承力结构、隔热层以及防热层分别分割成等厚度的N1、N2以及N33个节点，内壁面为节点1。

图2 多层防热结构离散节点示意Fig.2 Schemetic of Discrete Nodes for Multi-layer Thermal Protection System

防热层内部节点n的导热方程可离散为

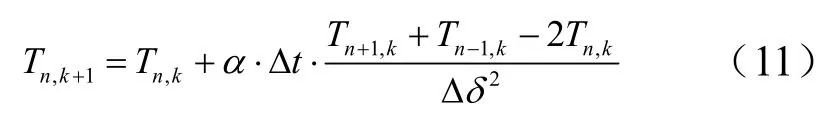
式中α为防热层材料的热扩散系数；下标k表示当前时刻参数；下标（k+1）表示下一时刻参数；tΔ表示时间步长；δΔ 为节点间距。

隔热层与承力结构交界面节点在第k+1时刻导热方程可离散为

式中下标1与下标2分别表示承力结构与隔热层参数。承力结构内壁面为绝热边界条件，承力结构内壁面节点在第（k+1）时刻的温度满足方程：

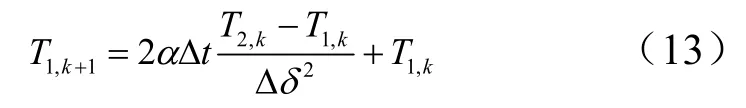
求解过程中，首先依据外界热环境计算烧蚀速率以及烧蚀表面温度Tw，如果外壁面温度低于烧蚀温度Tw，不考虑烧蚀过程，外壁面与空气对流传热，外壁面温度满足方程：

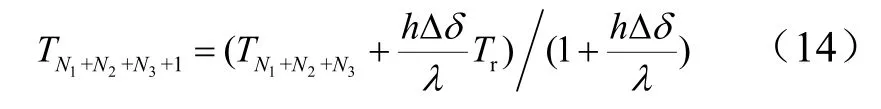
式中Tr为来流气体恢复温度；h为来流气体与防热材料表面的对流换热系数。如果外壁面温度超过烧蚀表面温度，外壁面出现烧蚀后退，将烧蚀时外壁温度作为计算的外边界条件，即：

若烧蚀持续时间为t，则热层节点间距离调整为求解式（11）～（15），可得各节点温度随时间变化关系。

假设防热层、隔热层与承力结构厚度分别6 mm、6 mm以及3 mm，空气恢复焓为3000 kJ/kg，冷壁热流为3150 kW/m2，热防护材料物性参数见表3。

表3 热防护材料物性参数Tab.3 Properties of Thermal Protection Materials

采用ANSYS软件以及本文模型计算得出承力结构与隔热层界面温度随时间变化对比如图3所示，飞行器飞行末秒（第70 s）时多层热防护结构沿着厚度方向温度分布对比如图4所示。由图3与图4可见，本文传热模型计算结果与有限元软件计算结果吻合，最大温差为0.7 ℃。因此，本文计算方法能准确预示多层热防护结构热传导过程。

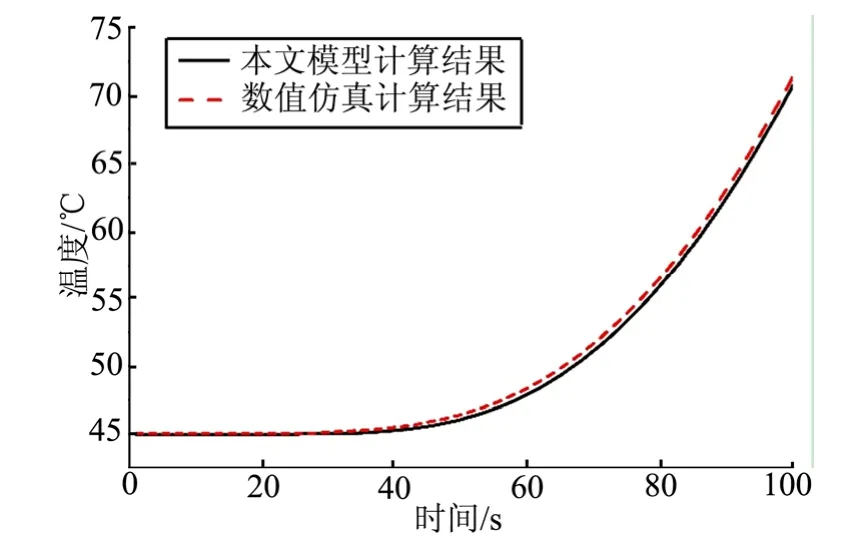
图3 承力结构温度随时间变化结果对比Fig.3 Comparison of the Bearing Structure Temperature

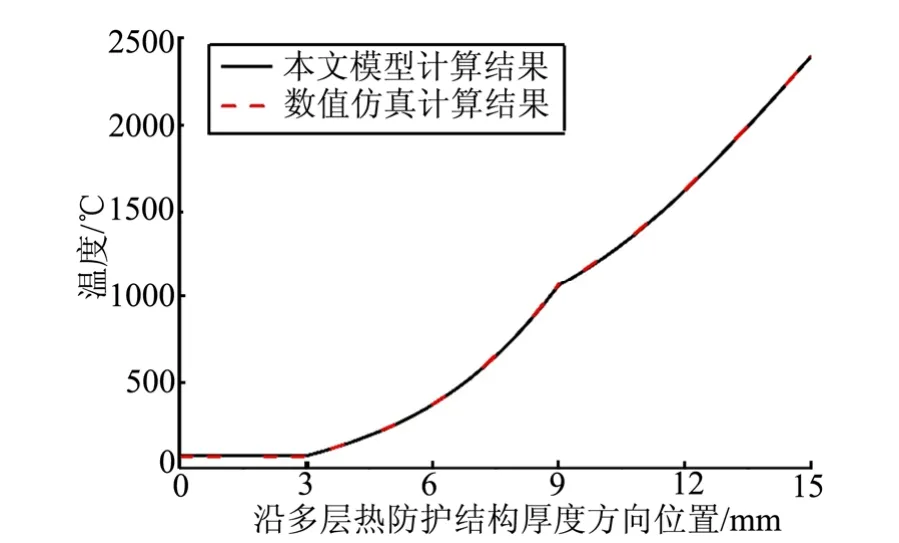
图4 飞行末秒热防护结构温度分布计算结果对比Fig.4 Mparison of Temperature Distribution inThermal Protection System

3 多层热防护结构温度响应特性

3.1 多层热防护结构温度分布

假设防热层、隔热层、承力结构厚度分别为5 mm、4 mm、3 mm，各层材料属性如表3所述，空气恢复焓为3000 kJ/kg，冷壁热流为3150 kW/m2，考虑防热层烧蚀，第10 s、40 s以及70 s时多层热防护结构温度分布如图5所示。

图5 不同时刻多层防热结构温度分布Fig.5 Multi-layer Thermal Protection System Temperature Distribution for Various Time

由图5可见，气动热环境下，热量由防热层外侧向防热结构内部传递，最终导致承力结构温度升高。随着防热层外侧烧蚀，防热层厚度逐渐降低，进一步加速了防热结构内温度升高。此外，由于隔热层材料导热系数小于防热层材料导热系数，热量传递到承力结构后（40 s后），隔热层内温度梯度显著大于防热层内温度梯度，因此，在满足隔热层温度、烧蚀裕度以及工艺要求前提下，增大隔热层厚度能提高防热性能，进而能够减小所需的防热层厚度，降低热防护系统的整体体积与重量。

3.2 多层热防护结构厚度分布对温度响应特性的影响

假设多层热防护结构承受3.1节所述气动热环境，飞行器飞行时间为70 s，承力结构、隔热层以及防热层总厚度为12 mm，飞行器飞行末秒承力结构温度随防热层厚度的变化如图6所示。由图6可见，随着防热层厚度增大，承力结构温度升高。分析原因可知，承力结构、隔热层以及防热层总厚度不变，随着防热层厚度增大，隔热层厚度降低，由于隔热层导热系数低于防热层，隔热层厚度降低导致防热性能下降。此外，防热层厚度相同时，随着承力结构厚度增大，隔热层厚度降低，防热性能下降，导致飞行器飞行末秒承力结构温度升高。因此，在本文热环境条件以及防热层与隔热层热物性参数条件下，增大隔热层厚度能提高整体防热性能。

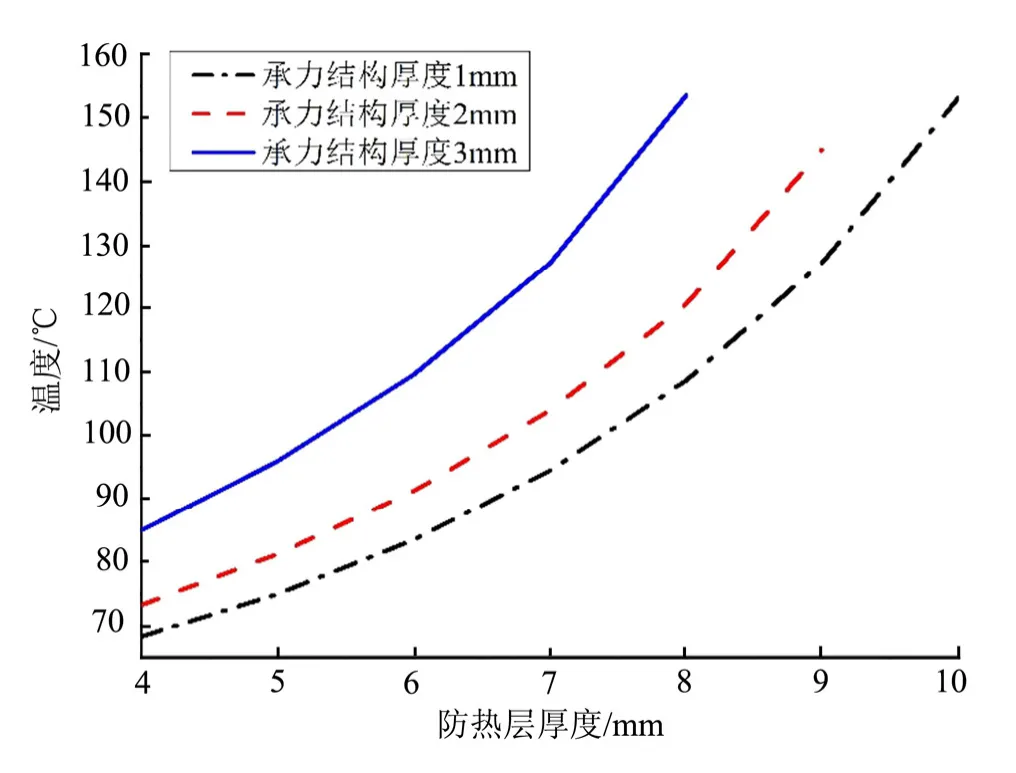
图6 飞行末秒承力结构温度随防热层厚度的变化Fig.6 Variations of Bearing Structure Temperature with Thermal Protection Layer Thickness at the End of the Flight

4 结 论

本文建立了气动热环境下防热材料烧蚀模型，提出了烧蚀导致的变厚度多层结构传热数值计算方法，形成了多层热防护结构烧蚀传热模型，分析了气动热环境下多层热防护结构温度分布随时间的变化，并进一步研究了多层防热结构厚度分布对防热效果的影响，得出的主要结论如下：

a）本文提出的防热材料烧蚀模型以及变厚度多层热防护结构传热模型具有较高精度，可用于传热分析；

b）飞行器飞行过程中，热量由防热层外侧向承力结构传导，热量传导到承力结构后，隔热层温度梯度大于防热层温度梯度，隔热层比防热层热防护性能更优，因此，满足隔热层温度、烧蚀裕度以及工艺要求前提下，增大隔热层厚度能提高热防护性能，减小所需热防护厚度，降低热防护系统整体体积与重量；

c）承力结构、隔热层以及防热层总厚度保持不变时，飞行器飞行末秒，承力结构温度随着防热层厚度增大以及承力结构厚度增大而升高。