运载火箭大直径螺栓承受拉弯耦合载荷失效判据研究

乐 晨，徐卫秀，杨 帆，曾杜娟，侯 杰

（1. 北京宇航系统工程研究所，北京，100076；2. 西北工业大学，西安，710072）

0 引 言

随着中国运载火箭壳体直径不断增大，载荷随之增加，在关键传力点，逐渐使用大直径螺栓承力。由于其力学环境复杂，这些螺栓通常使用强度高、塑性好的材料设计生产。应用场景主要在传递集中力的结构，如壳段点式连接、捆绑连接、发动机机架连接等。

在以往火箭结构研制过程中，出现过关键传力螺栓提前破坏的情况，发现是由受拉螺栓承受附加弯矩导致。在机械设计手册中，明确提出螺栓连接应避免这种情况出现[1]，前提是被连接件刚度远大于连接件刚度[2]。但由于航天结构减重等需求，被连接件刚度难以数倍于连接件，由此出现局部杠杆效应，进而产生附加弯矩。杨帆等人通过研究爆炸螺栓连接结构受力，提出依据杠杆效应和附加弯矩局部变形效应修正螺栓所受轴力，以此作为失效判据[3]。这种修正方法是从外部结构参数出发，不涉及材料塑性，是工程上便于指导设计的近似方法。

本文目标是从受力机理开展研究，并利用试验和仿真验证，寻找塑性下螺栓失效判据。在后文中，首先从弹塑性基本理论入手，对圆截面梁承受弯矩进入塑性后等效轴拉力进行理论分析。然后对大直径螺栓开展承受拉弯耦合试验研究。之后通过仿真复现试验，提取螺栓破坏截面轴力和弯矩，将计算总轴拉力与出厂破坏值对比作为失效判据，用于确定附加弯矩等效轴拉力塑性折减系数。

1 螺栓受弯折合轴拉力理论分析

1.1 线弹性下弯矩折合轴拉力推导

螺栓承受拉力和弯矩，可使用梁的塑性弯曲理论开展研究分析。

假定螺栓截面保持原形，当其承受弯矩时，在线弹性小变形的范围内，可通过材料力学公式计算受拉侧最大拉力。再以最大拉应力失效准则，可推导出弯矩相当于拉力作用：

式中M为弯矩；R为半径；TM为折合轴拉力；k为折减系数，线弹性条件下等于1，后文研究其在塑性下的取值。式（1）的推导过程与杨帆等人的研究类似[3]。

1.2 考虑塑性的弯矩折合轴拉力推导

假设螺栓材料本构为理想弹塑性，当螺栓受拉力进入塑性时，圆截面保持不变，截面都进入塑性，有：

式中T为拉力；R为半径；σs为屈服极限。

当梁受弯矩时，引入梁的塑性弯曲理论[4]，仍然保持平截面假设，对于中间截面，开始时梁受拉和受压最外侧同时达到屈服极限，随着弯矩继续增加，内部材料逐渐达到屈服，具体如图1所示。

图1 截面受力状态Fig.1 Section Force State

应力分布可表示为

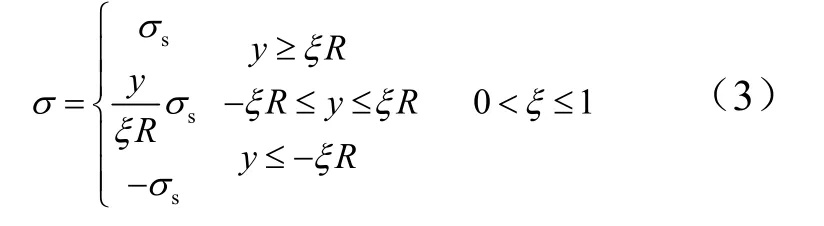
式中ξ为弹性部分材料高度系数。

根据这种应力分布，可得弯矩：

可以看出当ξ=1时，弯矩退化成材料力学线弹性小变形时状态。通过对比式（3）、（4），可得折减系数

当截面全进入塑性，即ξ→0，可以证明折减系数的极限，这与手册中一致。

进一步作图，可得折减系数随ξ变化曲线见图2。

图2 折减系数k随ξ变化Fig.2 Change Curve of Correction Coefficient k with ξ

在实际工程分析中，材料本构通常使用双线性随动强化模型，输入材料参数包括屈服极限，断裂极限和延伸率。此时截面应力状态如图3所示。应力分布可用式（7）表示：

式中1σ为最大应力，低于断裂极限 bσ。

图3 截面受力状态Fig.3 Section Force State

根据这种应力分布，可得弯矩，见式（8）：

进一步可推导出折减系数：

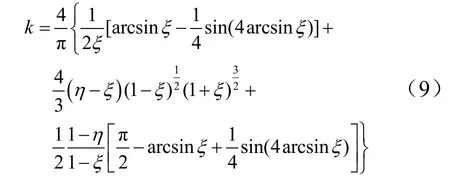
式中η为屈强比，当时，弯矩（8）会退回式（4）。做折减系数k随ξ、η变化曲线如图4所示，当η=1时，曲线退化成图2。

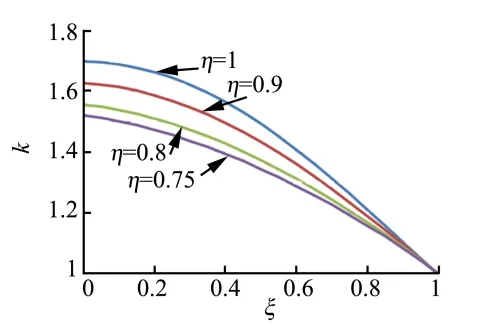
图4 折减系数k随ξ，η变化Fig.4 Change Curve of Correction Coefficient k with ξ，η

1.3 泊松比的影响

为了简化推导，上述推导未考虑材料泊松比效应。泊松比效应只影响梁受轴拉，因为其受拉时圆截面积半径变小，从而影响轴拉力积分。而弯矩则不因面积改变而改变，因此泊松比效应对折减系数有一定影响。在线弹性阶段，这种效应不明显。主要进入塑性后，轴拉力使得圆截面半径明显变小，弯矩则会因应力分布不均，导致圆截面变成椭圆，对折减系数有一定影响。由于拉应力和半径是迭代求解，因此工程算法不能得到精确解，只能定性判断，下一步采用有限元进行案例分析。

1.4 有限元案例验证

为了验证上述推导及理论分析，应用Abaqus有限元软件建立典型算例，进行仿真分析。建立半径5 mm，长度50 mm圆柱，一端固支，一端施加载荷，分别施加纯轴拉和纯弯矩载荷，如图5所示，按照受拉一侧最大点应变（进入塑性后，也可使用塑性应变）达到相同值时，轴拉和弯矩作用效果等同的思路，从数值仿真角度研究弯矩和轴拉力的等效对应关系。

采用静力学考虑大变形计算。施加的拉力载荷大小为78540 N，弯矩载荷大小为251328 N·mm。

假想材料参数取值如下：E=210000 MPa，sσ=800 MPa，bσ=1000 MPa，延伸率δ=10%。

图5 有限元模型Fig.5 Finite Element Model

从两算例中提取同样点的应变，计算的折减系数随塑性应变变化关系如图6所示。由图6可以看出，在线弹性阶段，折减系数为1，进入塑性后，快速提升，稳定在1.72左右。

图6 典型算例折减系数随塑性应变变化Fig.6 Change Curve of Correction Coefficient with Plastic Strain for the Typical Example

图6和图4的差别主要体现在泊松比效应。另外应用有限元方法预估常用螺栓材料折减系数随塑性应变变化曲线见图7，并对比汇总于表1。

图7 常用钢材料塑性折减系数随塑性应变变化Fig.7 Change Curve of Correction Coefficient with Plastic Strain for Common Steel Materials

表1 常规材料螺栓承受弯矩的塑性折减系数Tab.1 Plastic Correction Coefficient of Common Material Bolts Subjected to Bending Moment

综上所述，可以看出进入塑性后，折减系数快速增加。对于常用螺栓材料，其值稳定在1.6～1.75，具体值可根据试验进一步修订。材料非线性参数对折减系数的选取影响较小。

2 典型连接结构试验研究

2.1 试验设计和实施

通过反复试算，设计出一套模拟实际结构传力路径的试验工装（见图8），使用万能试验机，开展地面试验研究。

图8 试验设备和加载情况Fig.8 Test Equipment and Loading Conditions

这套工装利用偏心加载方式，实现拉力-弯矩同时加载，并呈现杠杆效应。定义加载轴线和试验螺栓轴线之间的距离为偏心距，通过不同的偏心距，可改变弯矩和轴力比值，从而实现不同加载状态。试验设计了3种加载情况：偏心距为0 mm的纯轴拉状态，100 mm最大偏心状态，中间状态为55 mm。

试验设备包括：YDL2000型电子液压伺服万能试验机（最大载荷2000 kN）；LMS SCADAS数据采集系统；BX 120-3AA应变片，电阻120 Ω，灵敏度系数2.0±1%。

试验螺栓规格M30，螺距2 mm，螺栓材料使用表1中的材料3，由指定厂家按设计要求生产。螺栓出厂拉伸破坏值如表 2所示。试验方案参考GJB715.23A-2008、GJB715.23A-2015等相关标准进行制定。通过试验机系统记录夹头的相对位移和力，形成载荷位移曲线，反映螺栓的破坏载荷；通过应变片和数据采集系统记录螺栓试件的应变，可以监控线性阶段拉弯耦合加载情况。试验分组情况如表3所示，共3组，每组3个子样，共9次正式试验。

表2 M30螺栓出厂参数Tab.2 M30 Bolt Parameters

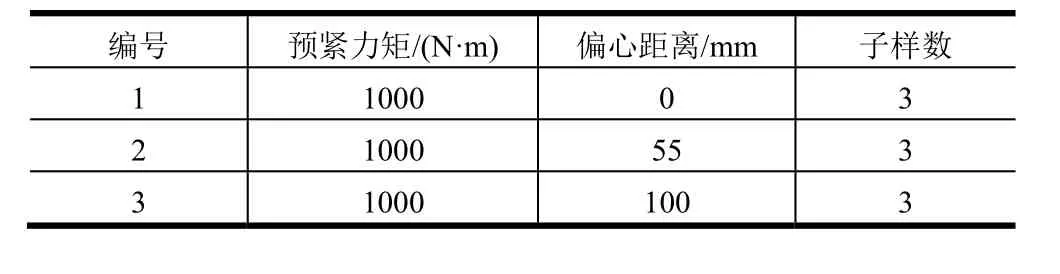
表3 试验分组情况Tab.3 Test Group

2.2 试验结果及分析

9次正式试验全部螺栓子样都在第1扣螺纹处破坏，破坏模式完全一致，破坏情况如图9所示，试验机记录的试验破坏载荷汇总于表4，同一状态破坏载荷相近，试验数据有效。

从试验结果中可以看出，0 mm工况下，螺栓破坏加载载荷均值848.9 kN，是出厂破坏载荷均值886.7 kN的95.7%，说明试验工装依然存在较小的杠杆效应，但可接受，能够为拉偏工况提供参考。

图9 试验破坏情况Fig.9 Failure of Bolts and Nuts

表4 试验结果汇总Tab.4 Summary of Test Result

3 失效判据研究

3.1 有限元试验预示建模

为了充分利用试验数据，对试验工装和螺栓进行精细化建模（如图10所示），模型包括工装。螺栓模型建立了螺纹，使用粘接式处理螺栓本体和螺纹牙[5]。在强度上，含螺纹模型比光杆模型更准确[6,7]。

0 mm工况计算结果呈现纯轴拉状态，验证了试验中0 mm状态的受力状态。随后对两个拉偏工况开展计算复现用于确定附加弯矩塑性折减系数。

图10 试验工装有限元精细化建模Fig.10 Test Tool of Finite Element Model

3.2 计算结果分析

按表4所述试验情况，两个拉偏工况试验加载的破坏载荷均值分别为511.8 kN、382.9 kN。通过3.1节建立的试验工装精细化模型对两个拉偏工况进行计算，当施加载荷达到试验加载破坏值时，查看计算情况。结果表明，两种工况下工装变形呈现局部杠杆效应，在螺栓受力的第1螺纹处出现超过30%的塑性应变，并且截面塑性贯穿。螺栓破坏截面计算结果示意如图11所示。

图11 破坏时刻螺栓塑性应变分布Fig.11 Plastic Strain Distribution of Bolts at the Moment of Failure

进一步通过后处理方法[8]提取破坏处截面的螺栓拉力和附加弯矩，将计算结果汇总于表5。

表5 螺栓计算结果汇总Tab.5 Summary of Bolt Calculation Results

3.3 塑性折减系数讨论

按表5的螺栓受力情况，可进一步计算螺栓承受的总轴拉力，即将轴力和附加弯矩折合的轴拉力相加。其中附加弯矩的折合轴拉力根据前文推导的式（1）计算，计算半径按螺栓截面积621 mm2[9]取值14.06 mm，折减系数k按多个取值将结果分别汇总于表6、表7。

表6 100mm偏心距离螺栓轴拉力计算结果汇总Tab.6 Summary of Force Results of Bolts with 100mm Eccentric Distance

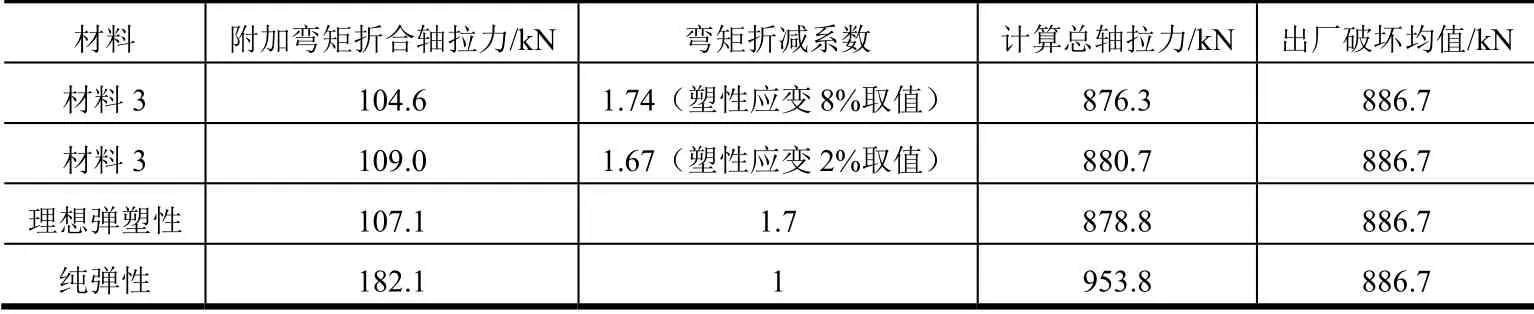
表7 55mm偏心距离螺栓轴拉力计算结果汇总Tab.7 Summary of Force Results of Bolts with 55mm Eccentric Distance

由表6、表7可以看出塑性折减系数在1.7左右，计算总轴拉力和出厂破坏均值接近，相差1%左右。若按纯弹性取值，则计算总轴拉力明显高于出厂破坏均值，说明对允许进入塑性的螺栓来说，其取值过于保守。以上结果证明了本文获得的弯矩塑性折减系数的正确性，综合工程应用考虑，塑性折减系数可按1.67保守取值。

4 结 论

a）本文首先通过理论推导和仿真，确定了理想弹塑材料螺栓承受弯矩的等效折合轴拉塑性折减系数在1.7左右，并获得现有材料取值范围在1.6～1.75。

b）开展某材料大直径螺栓拉弯耦合试验，进行两组拉偏工况螺栓破坏试验，每组试验子样破坏形式一致，破坏载荷相近，数据有效。

c）使用有限元精细化建模模拟试验情况，分析获得的破坏位置和试验完全一致。通过提取破坏时轴力和附加弯矩，并使用前文推导的公式计算总轴拉力。以此和出厂值对比作为失效判据。结果表明，螺栓在进入塑性条件下，弯矩等效轴拉塑性折减系数取值1.7附近时，两者相差约1%，验证了理论推导正确性。结合工程实际应用情况，折减系数可按1.67偏保守取值。

本文的研究成果目前仅局限在单一材料螺栓M30X2这一种规格上，为完善工作，后续可补充不同规格、不同塑性材料的螺栓继续进行计算和试验研究，形成一套可用于工程设计的指导规范。