基于小样本试验数据再入偏差折合及评估方法研究

严东升，贾平会，郭 珂，秦绪国，唐林卡

（北京航天长征飞行器研究所，北京，100076）

0 引 言

随着现代飞行器研制工作的深入开展，对飞行器命中精度分析和评估提出了越来越高的要求。受试验靶场限制，通常飞行试验射程与最终目标射程有相当差距，在试验次数、靶场范围受限条件下，飞行器精度评定则属于小子样、无全程信息命中精度评估问题，如何依据飞行试验结果对目标射程命中精度指标进行可靠评估成为一项关键技术难题。

本文通过分析再入干扰因素及其影响机理，建立飞行器再入偏差计算数学模型，计算了干扰条件下目标射程和试验射程再入偏差；基于试验数据分离试验射程条件飞行器再入偏差，并折算至目标射程状态；在此基础上应用飞行试验小子样再入误差评估方法，最终给出目标射程飞行器再入段落点偏差评估结果和精度指标评定结论，研究方法和结果为全系统命中精度指标评定奠定基础。

1 再入干扰因素及影响机理分析

飞行器再入飞行段受到以下干扰因素影响：大气密度偏差，大气温度偏差，风，初始质量偏差，烧蚀质量损失，气动系数偏差，初始再入攻角和边界层转捩等。通过分析各单项干扰因素产生的干扰力阐述其对落点偏差作用机理。

1.1 大气密度偏差

再入飞行弹道参数通常采用指定大气标准进行计算，而飞行器再入飞行过程中所遇到的实际大气与标准大气存在一定偏差量，这种偏差将导致落点散布。大气密度偏差将直接影响飞行器所受气动力，主要由其产生的气动阻力增量影响再入散布。相对密度偏差引起的阻力增量ΔD为

式中D为气动阻力，方向与阻力方向相同；ρ为密度；Δρ为密度偏差。Δρ为正时，密度增大，使阻力加大，因而使飞行器再入飞行时间增长、速度减小、弹道更加弯曲，因此落点偏近，即产生负射程偏差；Δρ为负时，将造成正射程偏差。大气密度偏差仅产生纵向射程偏差。

1.2 大气温度偏差

当考虑大气参数三要素密度、温度、压力时，把大气密度和温度作为独立变量，那么大气温度偏差在弹道方程中仅影响飞行马赫数Ma变化历程及气动特性，它产生阻力引起射程偏差。

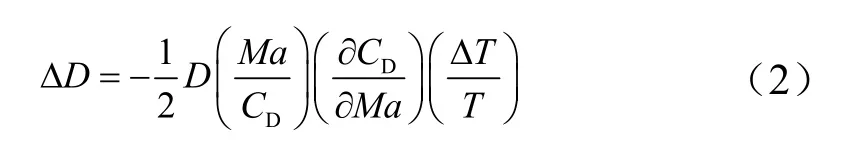
式中CD为阻力系数；T为温度；ΔT为温度偏差。

1.3 风干扰

进行再入段标准弹道设计时一般不计及风干扰影响，而飞行器实际再入飞行则不可避免存在风干扰。风将改变飞行器来流速度大小和方向，因此造成再入散布。在气象参数对再入散布影响中，风是主要干扰因素。根据飞行试验结果分析可知，风所引起的落点偏差通常十分突出。

高空风在不同高度层存在风速变化和风向变化。在散布计算中用风速WV和风向WA描述风矢量，并在水平面内分解为纵风和横风正交分量。风引起干扰力在速度坐标系中分量为

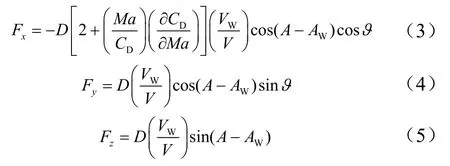
在线性假设条件下，纵风和横风对射程偏差影响相互独立，因此，纵风造成纵向射程偏差，顺风使落点偏远，逆风使落点偏近。横风将导致横向射程偏差，其偏差方向与横风方向一致。

1.4 初始质量特性偏差

由于存在设计制造误差，无法保证产品实际质量与设计名义值相等，因此存在初始质量偏差Δmo。初始质量偏差Δom将以干扰力形式影响纵向落点偏差。质量偏差引起干扰力为

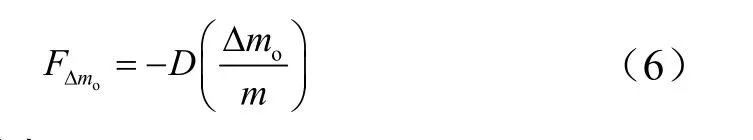
1.5 烧蚀质量损失

飞行器以高超声速再入大气层飞行，外表防热材料由于气动加热而出现烧蚀现象，使飞行器质量逐渐损失，因此引起质阻比发生变化，产生落点偏差。烧蚀质量损失Δam形成的干扰力为

干扰力FΔam大小直接与质量损失Δma大小成正比，由于Δam偏差总为负值，故此项干扰造成飞行器落点偏近。

1.6 气动系数偏差

再入弹道计算采用理论计算以及地面风洞试验综合结果给定的气动系数。其中，阻力系数对飞行器再入散布影响最大。两种因素导致阻力系数出现误差：其一，理论计算时所设大气气体状态和风洞试验所用条件与再入飞行时真实大气状态和环境条件存在差别，故理论计算和地面试验数据存在误差。其二，飞行器再入经历烧蚀/侵蚀后，其外形变化以及表面变得粗糙而不光滑，必然引起气动特性参数变化。气动阻力系数误差与大气密度偏差引起落点散布作用机理相同。气动系数误差ΔCD产生干扰力为方向与阻力方向相同。因此，气动阻力相对偏差

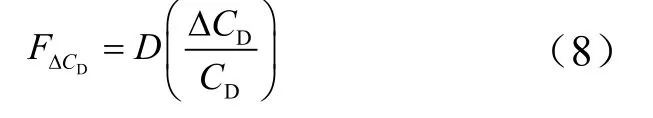
1.7 初始再入攻角

标准再入弹道通常按再入零攻角设计，而实际再入时刻可能出现的初始攻角则作为干扰因素予以考虑。

再入飞行攻角除了产生了附加阻力外还产生升力，因而将改变飞行速度大小和方向，造成明显的落点偏差。攻角引起气动阻力增大，使落点偏近；升力产生再入弹道方向变化则引起射程在纵向和横向方向上出现落点偏差。宜采用六自由度弹道计算模型计算分析攻角变化历程引起再入散布的具体偏差。

1.8 边界层转捩

当飞行器再入至大气层某一高度，绕飞行器表面的边界层流动，由于表面材料烧蚀/侵蚀局部粗糙度特性变化等原因，均能使层流边界层产生扰动和放大扰动，在一定条件下，层流流动失稳而发生转捩。边界层转捩除影响防热层设计、烧蚀外形、阻力特性、压心、气动阻尼动导数、配平特性外，对于落点散布同时带来不可忽略的影响。

边界层转捩对于散布的影响，通常按两部分处理：第1部分为对称分量，它考虑了边界层转捩所造成的阻力系数增量影响，可由阻力偏差予以考虑；第2部分为非对称分量，它考虑旋转转捩前阵面不对称气动力矩的影响。

根据相关文献研究结果[1～4]，边界层转捩非对称分量产生落点偏差可按如下近似公式估算：

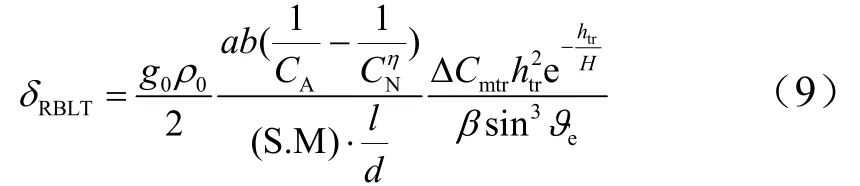
式中g0为标准引力加速度；ρ0为海平面大气密度；为轴向力系数；为法向力系数对攻角导数；htr为边界层转捩起始高度；H为指数大气高尺度系数；S.M为静稳定裕度；l为参考长度；d为参考直径；β为弹道系数；ϑe为再入当地弹道倾角；a，b为决定边界层转捩完成高度期间的系数；为边界层转捩期间产生的俯仰力矩系数增量。

2 再入偏差干扰理论模型

飞行器弹道计算基本方程包括质心运动和绕质心转动方程。由于绕纵轴自旋在再入飞行中飞行器具有稳定作用，使再入总攻角呈振荡衰减变化趋势，工程上当振荡变化总攻角η峰值小于0.1°后，则用三自由度弹道方程代替六自由度弹道方程。因此，计算标准弹道，采用三自由度弹道方程，而考虑干扰因素作用时，除再入初始攻角干扰计算须应用全部六自由度方程外，其它干扰力是在标准弹道附近线性展开求出，仅采用质心运动方程。若同时存在包括再入初始攻角等多个干扰作用，则采用六自由度弹道方程计算。

飞行器状态参数X为

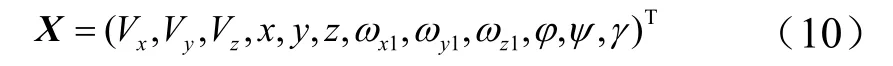
标准弹道方程为

干扰弹道方程为

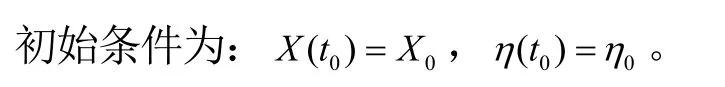
式中Fi为干扰作用引起的附加力，i=x,y,z 。

为便于获取任意高度处弹道数据，供计算落点偏差和偏差折合使用，采用了以高度h为自变量的微分方程。

2.1 质心运动动力学方程

根据理论力学动量定理和“固化”原理，飞行器在惯性坐标系质心运动动力学方程为[5]

式中m为飞行器质量；为绝对加速度；为合外力。

飞行器在再入过程中仅受引力mg和空气动力R作用。

发射坐标系中，建立飞行器质心运动动力学方程为

式中Vx，Vy，Vz为发射系速度分量；x，y，z为发射系位置分量；φ，ψ，γ为发射系姿态角。

2.2 绕质心转动动力学方程

根据动量矩定理，飞行器相对质心转动方程为[6]

式中H动量矩矢量，H=Iω；I为惯量张量矩阵；ω为飞行器角速度矢量；∑M为合外力矩。

通常在飞行器体轴坐标系中写出绕质心转动动力学方程：

式中ω1x，ω1y，ω1z为发射系角速度分量；η，α，β为总攻角、攻角和侧滑角。

2.3 运动学方程

建立飞行器运动学方程：

式中h为飞行高度；V为飞行速度；ϑ为当地弹道倾角。

2.4 再入落点偏差解算

应用上述再入弹道计算模型和方程，首先计算无干扰标准弹道，即取Fx=Fy=Fz=0，对应射程为L*，偏离标准射击平面侧向距离为H*。在考虑干扰因素作用时，按干扰作用机理取Fx，Fy，Fz和再入初始总攻角0η不同时为0，解算干扰弹道，射程为L，偏离标准射击平面的侧向距离为H。那么，干扰因素引起纵、横向偏差为

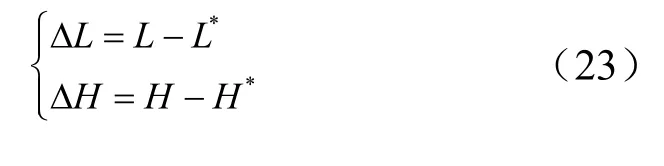
3 目标射程和试验射程再入偏差计算

针对目标区极限偏差干扰因素条件，利用上述再入偏差计算模型，计算给出了目标射程和飞行试验射程（试验射程1、试验射程2）条件下飞行器再入落点偏差结果。

3.1 目标射程飞行器再入偏差

根据飞行器再入点弹道参数，目标射程飞行器再入偏差理论计算结果见表1，目标点高程取Ch=0 m。

表1 目标射程再入偏差计算结果Tab.1 Reentry Deviation for Target Range

3.2 试验射程飞行器再入偏差

根据试验靶场条件，飞行试验包括试验射程1和试验射程2两种状态，按再入点弹道参数和各靶场实际目标点高程Ch，飞行器再入偏差理论计算结果分别见表2和表3所示。

表2 试验射程1再入偏差计算结果Tab.2 Reentry Deviation for Test Range 1

表3 试验射程2再入偏差计算结果Tab.3 Reentry Deviation for Test Range 2

续表3

4 再入误差折合及评估

由飞行试验结果分离给出飞行器再入偏差，利用再入偏差折合系数，将其折合至目标射程状态，采用置信区间估计法，从而得到基于小子样试验数据目标射程再入偏差评估结果。

4.1 再入偏差折合系数

在考虑主要干扰条件下，再入落点偏差对不同射程、不同落点高程的相互折合可用如下折合公式表示：

式中ΔL，ΔH分别为目标射程弹道纵、横向落点偏差；分别为飞行试验弹道纵、横向落点偏差；分别为各偏差对目标弹道纵横向偏差偏导数；KΔL，KΔH分别为纵、横向落点偏差折合系数；j=1,…,n，分别代表初始质量偏差、再入初始攻角、阻力系数偏差、大气参数、风和转捩等主要干扰因素，通过飞行试验外测、遥测和气象测量获得。

将上述干扰加入飞行器再入干扰弹道中进行计算，解算出各自引起的落点偏差等参数。

各飞行试验射程至目标射程飞行器再入偏差折合系数KLΔ,KHΔ结果如表4所示。

表4 试验射程对目标射程再入偏差折合系数Tab.4 Reduced Coefficience of Test Range to Target Range

4.2 试验射程再入偏差分离及折合结果

飞行试验可获取飞行器外测参数及相应外测参数精度数据。利用头体分离点飞行器高精度外测参数作为初始条件，计算标称状态下被动段弹道，得到飞行器落点参数，与目标点和实际落点相比较，得到主动段、再入段干扰引起的飞行器落点偏差。

飞行试验飞行器实测落点相对目标点纵、横向偏差记为ΔL实,ΔH实。

用头体分离点外测参数计算飞行器标称被动段弹道，其计算落点相对目标点纵、横向偏差，称为主动段干扰引起的飞行器落点纵、横向偏差，记为ΔL主,ΔH主。

而计算落点对实测落点纵、横向偏差则为再入段干扰产生的落点纵、横向偏差，记为ΔL再,ΔH再，即：

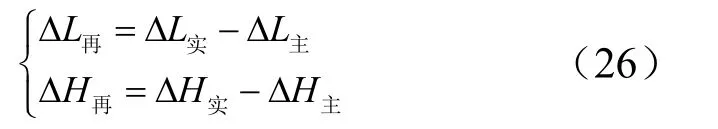
头体分离点外测参数总是存在测量偏差。根据头体分离点飞行器速度、位置分量对落点纵、横向偏差偏导数和外测参数精度iqσ，可计算再入段落点偏差估计精度σΔL、σΔH,具体公式如下：

式中qi代表Vx,Vy,Vz,x,y,z。

试验射程1和试验射程2飞行试验结束后，按上述方法分离给出了相应飞行试验状态下飞行器再入落点偏差结果，并折合至目标射程，具体数据见表5和表6。

表5 试验射程1再入偏差分离及折合结果Tab.5 Reentry Deviation Separation and Reduction for Test Range 1

表6 试验射程2再入偏差分离及折合结果Tab.6 Reentry Deviation Separation and Reduction for Test Range 2

4.3 小子样试验再入偏差评估结果

对小子样飞行试验，射击密集度评定大纲中给定评估方法为单侧区间置信上界估计法。根据给定置信水平1-α，目标射程再入段纵、横向偏差方差置信上界估计公式为[7]

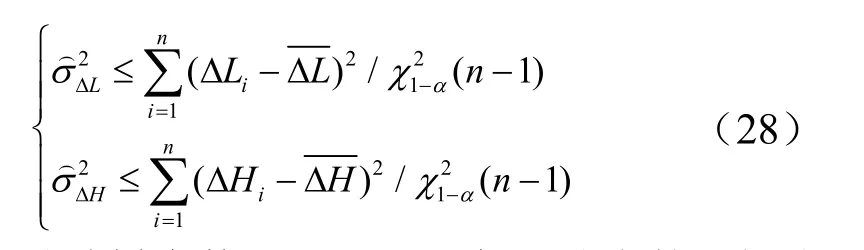
式中n为试验样本数；为2χ分布的下侧分位数[8]，取置信水平1-α=0.8，

5 结束语

本文开展了飞行器再入误差分析与评估研究，根据相关飞行试验结果，进行了再入误差分离方法及应用研究，将试验弹道再入偏差折算至目标射程弹道再入偏差，提升了误差分离能力。在此基础上构建了基于飞行试验小子样条件下再入偏差评定方法，得出了适用于飞行器再入偏差评定详细数学模型和实用计算方法。