基于ARIMA模型的城市路网交通运行指数预测研究

董洁霜，方天源，周亦威

（上海理工大学 管理学院，上海 200093）

0 引 言

城市道路交通运行状态数据，是交通出行决策和拥堵治理的关键。路网高峰行程延时指数，简称“延时指数（Delay Index）”，作为城市道路路况重要指标之一，其根据交通部门提供的实时监控和各地图导航后台返回的大数据综合判断，为出行者提供导航路线参考。

现状研究主要针对拥堵延时指数的空间属性。袁浩［1］等人研究人口、用地属性、交通基础设施密度等空间异质属性对拥堵延时指数的关系。冯海霞［2］等人通过地理加权回归（geographically weighted regression，GWR）模型，定量分析拥堵延时指数与空气质量指数的强相关性。汪传雷［3］等人利用熵值法研究不同车型对拥堵延时指数的影响程度，提出分车型的治堵措施。胡成雨［4］等人基于Kruskal－Wallis 检验，对中国不同城市拥堵延时指数进行比较和排名，量化各城市的交通健康差异情况。相较统计理论模型，深度学习的方法对短时交通流数据的捕捉能力更好［5］，但统计学模型适用于长时间跨度的交通流状态指标分析预测。相关研究表明，城市道路拥堵延时指数在时间上有明显的周期特性［6］。其表现为，节假日的始末段拥堵延时指数较高，工作日的周一、周五拥堵延时指数高于该周的其它工作日。但实际上，在长跨度的时间序列数据中，受天气条件、临时交通管控政策、交通基础设施建设进度等多因素影响，并非周一、周五拥堵延时指数都比其余工作日高。如果在建模分析时默认存在时间序列周期性，会对区域交通运行状态指标研判工作有一定的干扰。

综上所述，研究大多关注空间效应对拥堵延时指数的影响，时间层面受到数据样本量的限制会适当回避。然而，与时间层面影响最大的是政策效应［7］。例如：单双号限行、小汽车牌照申领指标限制、鼓励错峰出行等。随着时间推移，各个交通管控措施的依次（或叠加）实施，都会对拥堵延时指数产生影响。工作日的拥堵延时指数对市民的通勤出行更具有引导意义。工作日高峰时期拥堵延时指数的上升，主要是市民通勤导致的交通流集聚在部分道路，相较节假日，工作日的城市路网拥堵延时指数一般更高，这是工作日的出行时间更集中，方式单一且路径基本固定所导致。本研究通过将杭州西湖区2019年9月15日至2021年9月15日（共计499个数据样本）每日的高峰拥堵延时指数进行时间序列分析（剔除节假日），利用ARIMA模型进行样本内数据预测和样本外数据预测。同时考虑新冠肺炎疫情特殊时期的交通管控措施政策对拥堵延时指数的影响。

1 ARIMA模型设计

ARIMA（Autoregressive Integrated Moving Average model）模型综合考虑了时间序列的趋势变化、周期性和随机干扰［8－9］。其建模步骤依次为数据预处理、模型识别、模型诊断及检验、模型预测。

ARIMA（p，d，q）模型原理如下：

其中，E(εsεt)＝0，s ＜t；xt表示时间序列数据，xt与xt－i（i＝1，2，…，p）相关；εt表示残差项，εt与εt－i（j＝1，2，…，q）相关；B表示延迟算子，满足Bn xt＝xt－n；p表示自回归阶数；q表示平均阶数；d表示差分阶数；▽表示差分算子；▽d＝(1－ B)d。

式（1）中的自回归系数多项式的具体表达式如下：

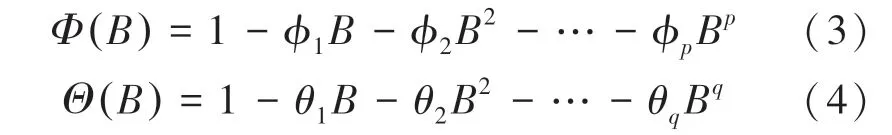
残差εt是独立于xt－i和εt－i的白噪声序列，满足：

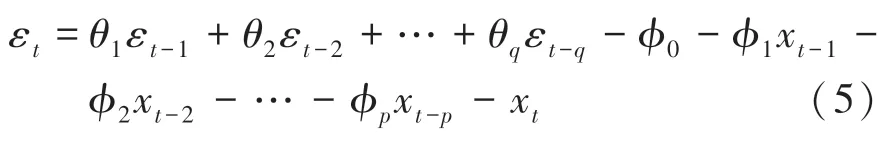
2 预测数据描述

此次研究的数据来源于高德智慧交通公共服务平台，数据类型为杭州市西湖区工作日的路网高峰行程延时指数（高峰时间为7：00－9：00 和16：30－18：30），数据时间跨度为2019 年9 月15 日至2021年9 月15 日，共计499 个样本数据。另外，为测试ARIMA模型在样本外的预测能力，补充时间跨度为2021 年9 月16 日至2021 年10 月15 日的工作日路网高峰行程延时指数数据。

路网高峰行程延时指数的计算原理源自旅行时间指数。旅行时间指数TTI（Travel Time Index）［10］是常用的城市拥堵程度的评价指标，其反映实际花费的行程时间与自由流花费行程时间的比值关系，与拥堵程度正相关，值越大表示交通运行状态越差。高德地图后台基于海量的轨迹数据，可以准确计算路网高峰行程延时指数，用直观的形式表达城市拥堵程度。

计算基本思想：定义一条路段link有两个连续的时间片，分别为t1、t2，路段的长度为S，则t1到t2这段时间内路段的平均速度v为2S／（t1＋t2）。同一条路段在一个时间片内，旅行时间指数为自由流速度和实际速度的比值。当轨迹覆盖度较低时，根据路段的长度和路况的可信度进行过滤。集合S的定义为所有路段link的集合，S＝｛link1，link2，link3，link4，…，linkN｝。集合中路段link的总数为N，Li为路段link的长度，Wi为路段link的权重，为路段link的自由流速度，Vi为实时路况速度。故计算方式如式（6）所示。

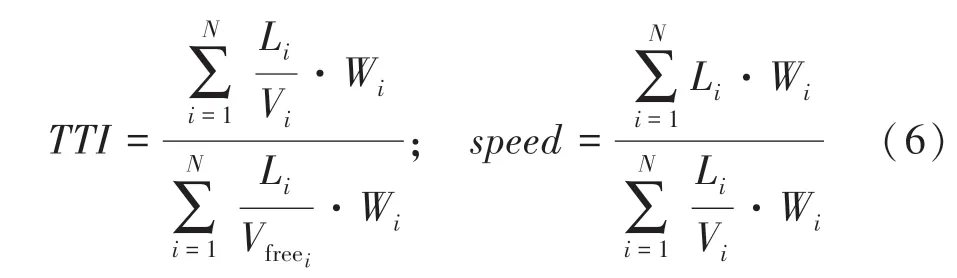
以上是对路段延时指数的计算方式，由每个路段的计算结果得到区域拥堵延时指数，计算逻辑如图1 所示。

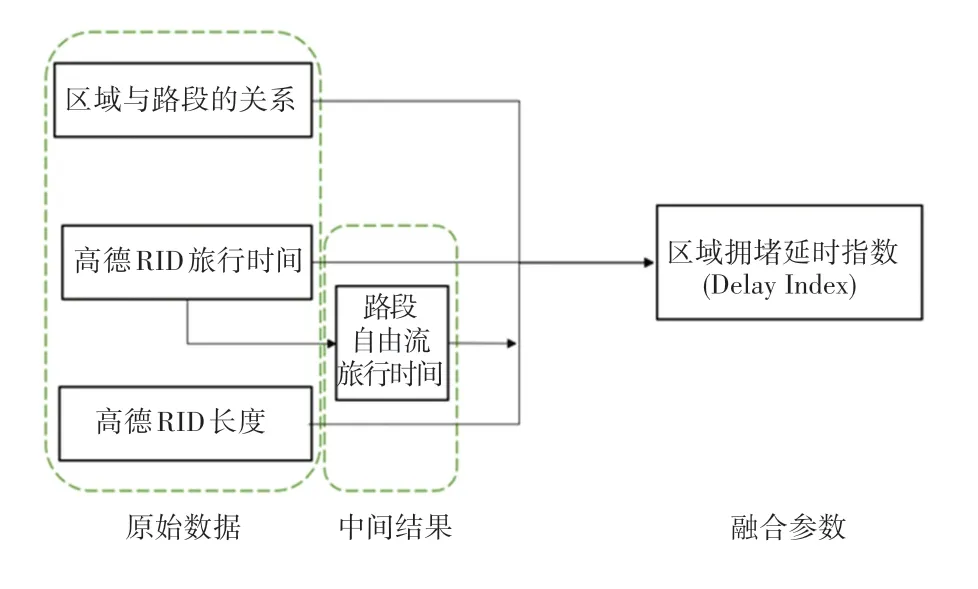
图1 区域拥堵延时指数的计算逻辑Fig.1 Calculation logic of the regional congestion delay index

3 方法与模型

3.1 模型实现

数据样本工作日延时指数时间序列如图2 所示。由于数据选取的是工作日的延时指数，从图中可见没有明显季节性特征。但在第91 个时间序列点（2020 年1 月23 日）处延时指数骤减，而当天正是武汉市发布“封城”通告时间。从该日开始，城市公交、地铁、长途客运暂停运营，全国各级市也随即响应相关交通出行和管控政策，城市路网的延时指数急剧下降。直到2020 年3 月2 日，随着复工复产的有序推进，杭州市西湖区的路网高峰行程延时指数自骤减后首次回到1.2 以上。

图2 时间序列（2019／9／15～2021／9／15）工作日路网高峰行程延时指数Fig.2 Weekday road network peak delay index of time series from 2019／9／15 to 2021／9／15

平稳性描述的是时间序列的统计性质关于时间平移的不变性。研究时间序列是希望通过时间序列的历史数据规律，得到其未来的一些预测。在模型运行前，对该时间序列进行ADF 单位根检验结果见表1。结果显示，P－value＜0.05，数据稳定，拒绝原假设。从ADF 单位根检验结果可以看出Test statistic＝－8.949 小于1%、Critical value＝－3.440。表明99%的置信区间下都满足数据平稳性，无需进行差分处理，即ARIMA（p，d，q）中参数d＝0。

表1 ADF 单位根检验Tab.1 ADF unit root inspection

使用自相关（ACF）与偏自相关（PACF）图判断ARIMA（p，d，q）模型中的p、q阶数，必要时可以用AIC（Akaike information criterion）、BIC（Bayes Information Criterion）检验进行再确定。自相关函数（ACF）是将有序的随机变量序列与其自身相比较，反映了同一序列在不同时序取值之间的相关性；偏自相关函数（PACF）是剔除了中间随机变量干扰，所得到的两个变量之间的相关性，之后计算两个变量之间的相关性。利用Stata 软件对序列进行自相关（ACF）图和偏自相关（PACF）图的绘制，其结果如图3 所示。

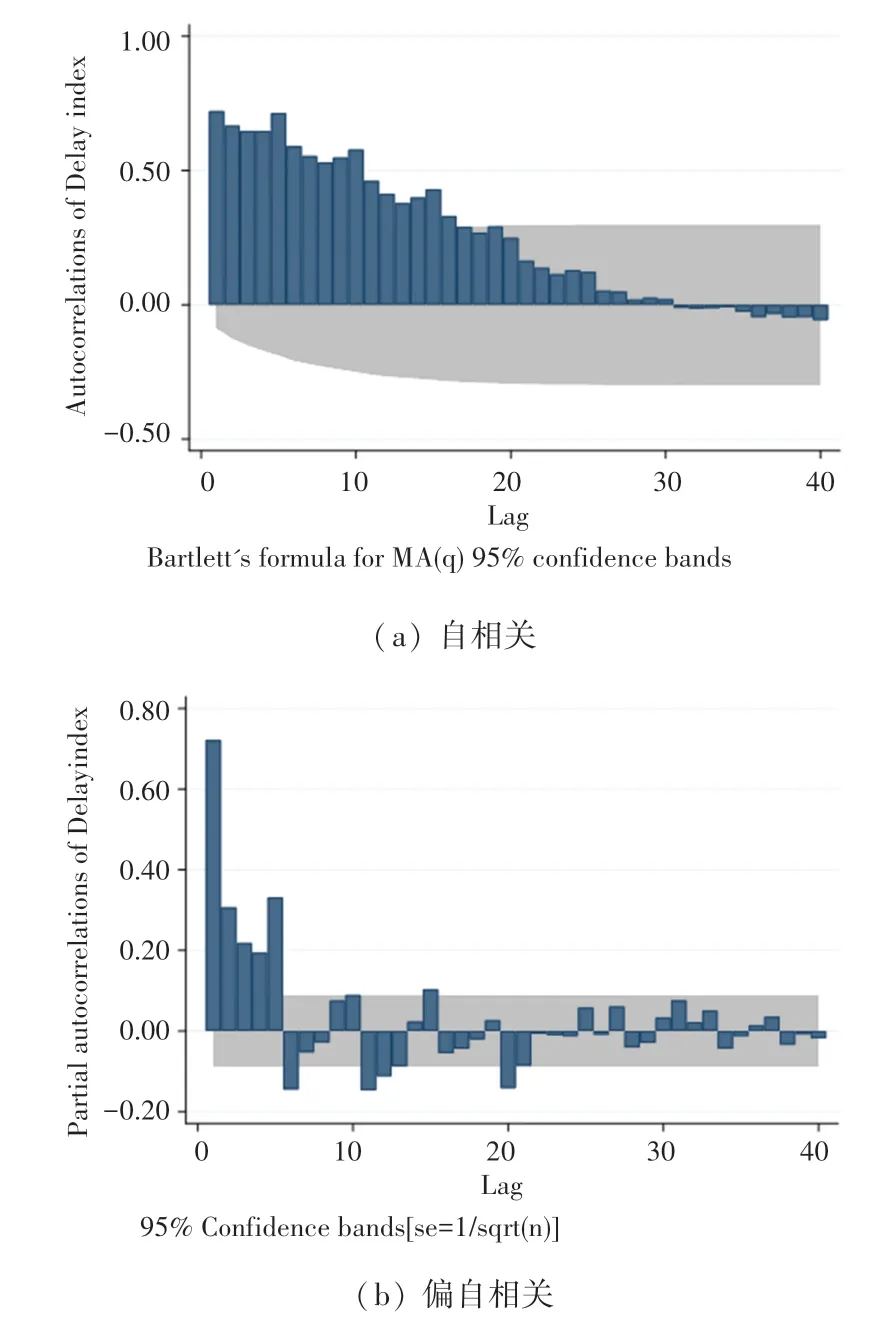
图3 研究序列的自相关（ACF）及偏自相关（PACF）图Fig.3 Autocorrelation（ACF）diagram and partially related（PACF）

从图3（a）中可以初步判断ACF 图拖尾，故q＝0。从图3（b）可以确定PACF 图截尾，p的取值可以为5、6、7、8。通过AIC、BIC 检验值最小原则，进行p值的再判断，结果见表2。ARIMA（6，0，0）模型中的AIC值和BIC值最小，故p＝6、q＝0、d＝0 为ARIMA（p，d，q）模型最优参数。

表2 AIC、BIC 值检验结果Tab.2 Test results of AIC and BIC value

拟合模型后，需要对残差序列检验，判断是否为白噪声。数据集中生成了新的残差序列，对得到的残差序列进行ADF 单位根检验，得到残差是平稳序列，见表3。模型检验结果如图4 所示。对残差进行Ljung－Box 检验后，通过白噪声检验（Q＝63.377 2，P＝0.010 7），从残差自相关（ACF）图来看，残差服从均值为0 的正态分布，此模型残差大部分落入95%可信区间，说明有效信息被充分提取，模型的有效性拟合效果较好。模型检验结果如图4 所示。

表3 残差的平稳性检验Tab.3 Residual stability test

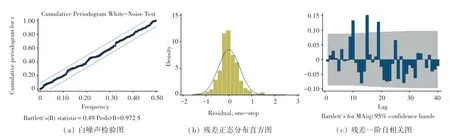
图4 模型检验Fig.4 Model Validation

3.2 模型预测

使用ARIMA（6，0，0）对模型进行样本内和样本外预测，结果如图5 所示。整体来看，预测线与实际线贴合程度较好。对样本外的延时指数数据进行预测发现，预测线逐渐呈现收敛状态，若样本外数据容量过大，会使预测数据趋于一个常量。样本内平均绝对百分比误差MAPE（Mean Absolute Percentage Error）为2.435 ＜10，样本外平均绝对百分比误差MAPE 为2.625＜10，说明模型的预测精度较高。

图5 预测线及实际线Fig.5 Prediction line and actual line

4 实验结果及分析

将实验结果从Stata 软件中导出，见表4，可见各项统计检验值均显著。从表5 可以发现，各阶滞后的z值均显著。拥堵延时指数预测值与实际值的绝对误差小、预测结果客观真实。

表4 ARIMA（6，0，0）模型统计检验值结果Tab.4 Statistical test value of ARIMA（6，0，0）model

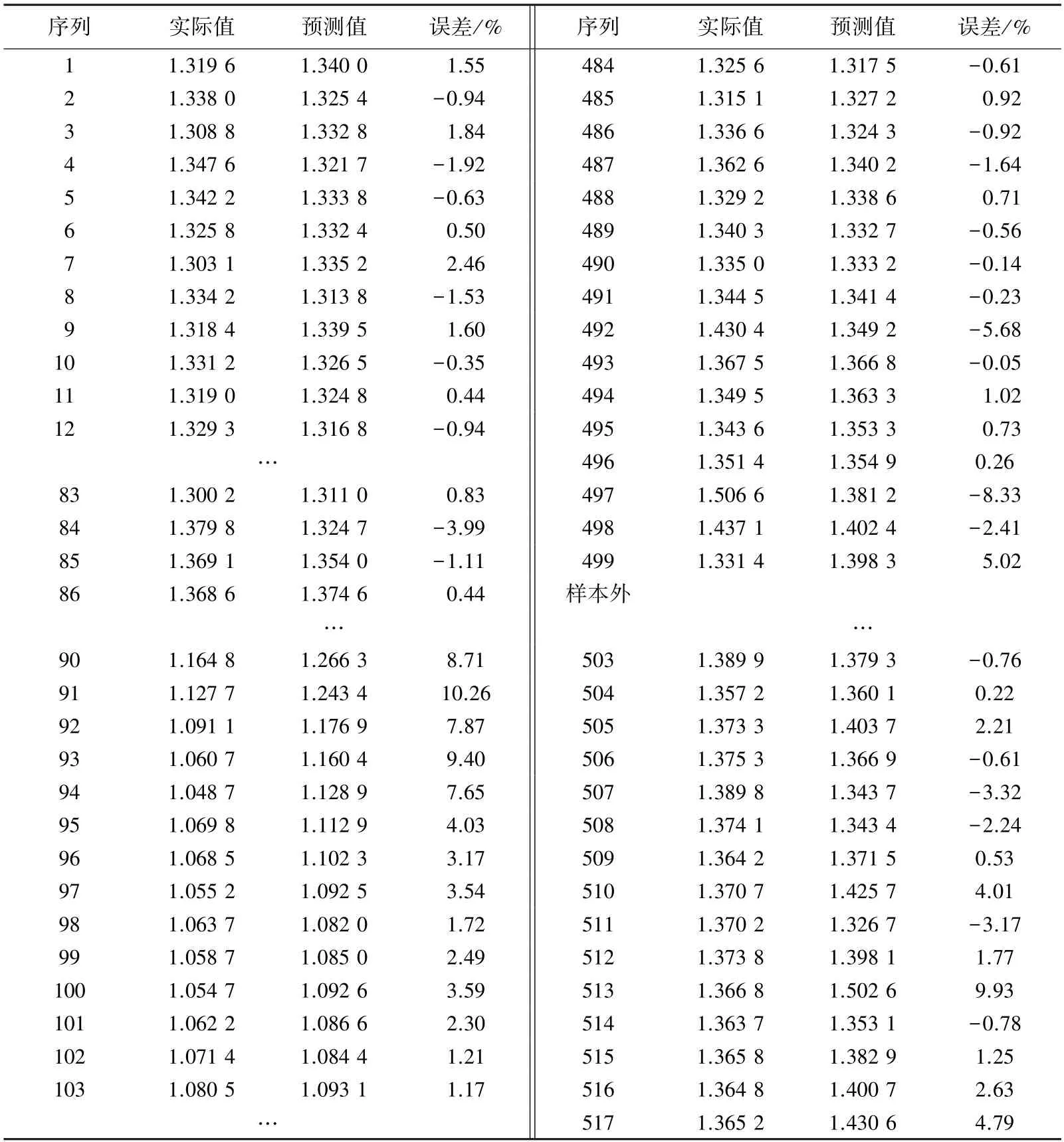
表5 拥堵延时指数预测值与实际值Tab.5 The prediction value and actual value of congestion delay index

为检验ARIMA模型在突变数据时间段内的预测韧性，考虑新冠肺炎疫情对延时指数的冲击，针对2020 年1 月14 日～2 月14 日延时指数实际值和预测值进行分析对比，如图6 所示。2020 年1 月23日是武汉“封城”开始日，全国各地包括杭州也随即响应特殊交通管制措施。整体看，路网拥堵延时指数从原来的1.4 左右下降到1.2 以下。通过该特殊时间段工作日路网高峰行程延时指数的实际值与预测值对比，发现在1 月23 日后预测值与实际值有一段数据“落差”，但很快两者又逐渐贴合，可见ARIMA模型的预测韧性较好。

图6 新冠肺炎疫情发生前后的延时指数实际与预测值Fig.6 The actual and predicted value of the delay index before and after the emergence of COVID－19

5 结束语

本文利用杭州市西湖区2019／9／15～2021／9／15连续工作日的城市路网高峰行程延时指数数据样本，建立延时指数的ARIMA 预测模型。同时考虑新冠肺炎疫情对城市道路交通运行状态的冲击，对样本内和样本外数据进行预测分析。对比结果误差小、精度高，证明ARIMA模型能够适应短时的数据突变，有一定的模型预测韧性，预测效果具有实用价值。未来研究将同时考虑长时间跨度下的空间因素变化对延时指数的影响。

研究过程到以下结论：

（1）新冠肺炎疫情特殊交通管控措施影响下，杭州市西湖区城市路网高峰行程延时指数显著下降，路网交通运行比往常工作日更畅通；

（2）ARIMA模型能够捕捉短时的数据突变并预测时间序列趋势，对时间序列预测客观有效；

（3）城市路网高峰行程延时指数能够为城市交通管理者和出行者提供出行参考，其历史数据、现状实时数据以及预测数据都具有研究意义；

（4）时间序列数据中含政策效应因子，政策效应对预测序列的影响不仅在冲击前后时间段，其影响可能会持续一段时间。