基于图像块相似性和稀疏先验的模糊图像盲去卷积复原
2021-03-01纪艳玲汤宫民
纪艳玲,汤宫民
(山东工程职业技术大学 信息工程学院,济南 250000)
0 引 言
通过电子设备采集到的图像在形成、储存、调制处理和信号传输的过程中,因为信道噪声或模糊等因素影响会产生失真,从而造成图像质量的退化[1]。对采集过程中退化的图像进行相关处理,从而得到与原始图像尽可能一致图像的过程称为退化图像的复原,其本质是图像退化的一个逆过程。作为一个基础且重要的底层计算机视觉问题,图像复原有很多经典的理论和使用方法,早期的逆滤波从频域的角度分析图像复原,基于扩散的偏微分方程和小波系数的统计特性推动了图像复原的发展;稀疏表示和字典学习在图像复原方面也取得了较大的成功。近年来,随着机器学习的快速发展,基于自然图像块建模的复原方法成为研究的热点[2]。本文针对图1 所示样本类型进行图像复原算法的研究。

图1 退化图像典型样本Fig.1 Typical samples of degraded images
1 基础理论
1.1 图像退化
采集图像质量退化的原理可以用公式(1)所示的数学模型来表示:

其中,x表示初始清晰图像;y表示采集后退化图像;k表示模糊算子;n是噪声;*是卷积运算。
通常可以假定噪声为高斯白噪声,服从均值为0,方差为σ的高斯分布,即n~N(0,σ)。如果模糊算子k已知,则称为图像非盲去卷积[3]。特别的,当k是狄拉克函数时,图像复原问题就变成了图像去噪。
在实际应用中,模糊算子k和噪声方差σ通常是未知的,这时的图像复原问题称为盲复原[4]。由于在退化方程中只有退化图像y是已知的,而清晰图像x、模糊算子k和方差σ均未知,从退化的图像中恢复出清晰图像是个病态问题。由于没有足够的信息保证待复原部分数据的正确性,通常需要利用先验知识对问题加以约束。
1.2 图像复原
通常可用公式(2)所示的损失函数来表示图像复原的整个过程[5]。
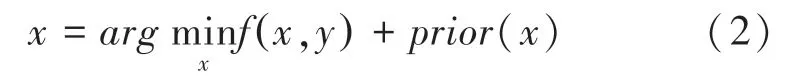
其中,f(x,y) 表示数据保真项,使得估计出的原始图像与退化图像在内容上保持一致,prior(x)则表示先验项,这是一个来自自然图像本身的特性。
这个损失函数可以从概率交付给与很好的解释,根据最大后验概率估计原理,对原始图像的估计可表示为公式(3):

其中,P(x |y)表示从原始图像x得到退化图像y的概率,P(x)表示图像x的先验概率,对上式取负对数,就可以得到图像复原的损失函数。
2 基于稀疏先验算法的模糊图像盲去卷积复原
对于模糊图像进行盲去卷积,难点在于对于模糊算子一无所知,这就需要一个先验性的知识,对原图及模糊算子进行预估初始化。
解决这一问题的思路是采用图像强度与梯度的L0 正则化[6]。首先,对图像进行gamma 矫正;其次,设置模糊算子大小,确定最大迭代次数,梯度滤波,用快速傅里叶变换去除模糊算子内的固体噪声,建立梯度幅度直方图,对模糊算子进行估计。
2.1 基于自然图像块强度与梯度的L0 正则化先验的盲去卷积
对于给定的模糊图像,在没有给定模糊算子的情况下,直接使用维纳滤波无法实现滤波,只能通过先验知识进行估计。本文借鉴传统露西-理查德森(Richardson-Lucy)的盲去卷积算法的同时,融合自然图像块强度和梯度的L0 正则化进行盲去卷积。
该算法由贝叶斯公式推导而来,因为使用了条件概率,即算法考虑了信号的固有波动,因此具有复原噪声图像的能力[7]。贝叶斯公式如公式(4)所示:
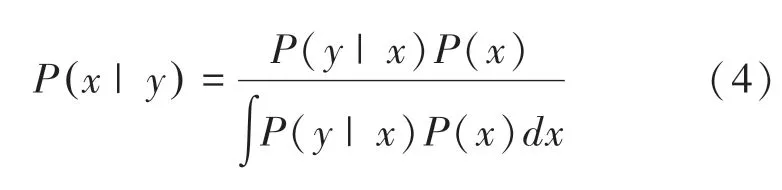
结合图像退化/复原模型,可以得到迭代函数,如公式(5)所示:

其中,fi就是第i轮迭代复原图像,对应贝叶斯公式中的p(x);g是退化函数,对应贝叶斯公式的P(y |x);c为退化图像。
假设退化图像各区域的模糊函数处处相同,那么可以将公式(5)化简为公式(6):

这就是路西-理查德森迭代公式,其中c是退化图像;g是退化函数;f是第k轮复原图像。
如果系统的退化函数PSF(g(x))已知,只要有一个初始估计f就可以进行迭代求解。在开始迭代后,由于算法的形式,估计值会与真实值的差距迅速减小,从而后续迭代过程f的更新速度会逐渐变慢,直至收敛。算法的另一优点就是初始值f >0,后续迭代值均会保持非负性,并且能量不会发散。
无噪声影响的盲去卷积需要两步进行复原,原因是既不知道原始图像f,也不知道退化函数g。算法执行流程如图2 所示。

图2 图像盲去卷积流程图Fig.2 Flow chart of image blind deconvolution
即在第k轮迭代,假设原始图像已知,即第k-1轮得到的fk-1,再通过R-L 公式求解gk,随后再用gk求解fk,反复迭代,最后求得最终f和g。因此,在求解最初,需要同时假设一个复原图像f0和一个退化函数g0。迭代公式如公式(7)和公式(8)所示:

同时,为了解决在复原图像内部灰度对比明显的地方和图像边界都出现的“振铃”问题,定义一个加权函数来减少图像中的“振铃”,该算法是在对图像和PSF 进行复原时,对每个像元根据|WEIGHT |数组进行加权计算。
2.2 基于强度和梯度先验的L0 正则化去卷积
借助于不同的自然图像先验信息,可以估计出不同的原始图像。常用的自然图像的先验信息有自然图像的局部平滑性、非局部自相似性、稀疏性等特征[8],本文在图像块相似性先验复原基础上加以稀疏度特征,从而实现更精确的电子设备采集图像的盲去卷积复原。
对于一幅模糊图像x,定义其强度稀疏度如公式(9)所示:

而其稀疏度,即先验条件,可表示为强度稀疏度和梯度稀疏度之和,如公式(10)所示:
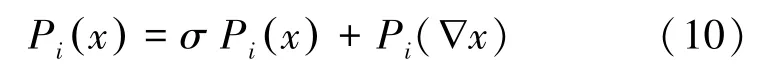
式中,σ为权重,Pi(∇x)为梯度稀疏度。
梯度稀疏度的最小化,本文采用L0 正则化方法实现,如公式(11)所示:
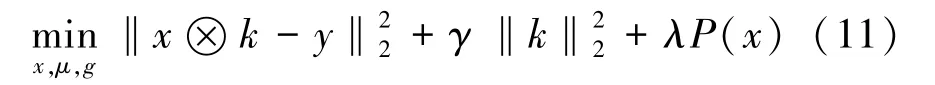
其中,x为清晰图像;y为模糊图像;γ和λ为正则化参数;k为模糊核;⊗为卷积运算符;‖‖2为正则约束项。
考虑到公式(11)无法直接求最小值,因此采用半二次分裂的优化方法,即固定x,μ,g中任意两个变量来交替求最小值。实验发现,采用梯度域预估模糊核比一般像素值预估模糊核效果要好。
3 结果分析
本文实验在Macbook air 1.8GHz Intel Core i5,8GB 内存的硬件环境和MacOS High Sierra10.13.3、Matlab R2017a 的软件环境条件下进行。
利用本文算法对模糊退化图像进行盲去卷积复原,样本复原图像及其最大值归一化后的模糊算子见表1。可以清楚看到,对于模糊文字、海报及实际车辆的复原效果较好。特别的,对于极度模糊的车辆,图像复原后可以清晰辨认车辆车牌号后6 位为B 8L358。

表1 退化图像复原结果图Tab.1 Restoration results of degraded images
4 结束语
利用退化图像与清晰图像之间部分相似性和稀疏先验条件构建数学模型,以提高采集图像的质量。首先,构建基于图像块期望的高斯拉普拉斯相似性模型,使计算机学习过程简化,速度加快;其次,通过概率统计中的近似最大后验估计算法,最终实现采集退化图像的复原。通过对典型退化图像样本的算法测试可以看出,该算法对于模糊图像的还原效果显著,具有极大的现实意义。
