分数阶时滞混沌系统的自适应模糊滑模同步
2021-02-28崔晓萌赵小山
崔晓萌, 赵小山
(天津职业技术师范大学理学院 天津 300222)
分数阶微积分作为对传统整数阶微分和积分微积分的扩展和推广,由于其具有建模动态行为、更大的稳定性等明显优势,因此一直应用于控制理论和工程学以提高目标系统的性能和鲁棒性以及遗传特性。在过去的几年中,前人研究了分数阶系统的一些显著鲁棒控制结果[1-3]。由于其在安全通信和控制处理中的潜在应用[4,5],分数阶动力学系统及其相关现象中的混沌同步研究日益受到关注。
为了提高非线性系统的控制性能和鲁棒性,许多非线性控制技术用于控制器设计,例如模糊控制[6,7]、神经网络控制[8]、滑模控制[9,10]和自适应控制[11,12]。另外,文献[13]提出了一种自适应模糊分数阶滑模控制(AFFOSMC)方法,保证了PMLSM的动子位置精密跟随给定。在现实生活尤其是工程中,时滞现象与不确定因素是普遍可以看到的,这样就会导致系统性能的不稳定性[14]。对分数阶混沌系统在不确定性和外界干扰下通过有限时间控制,可使系统在有限时间收敛到零,但是设计的控制器鲁棒性性能未能达到理想的效果。随着学者们的研究逐渐深入,发现在系统测量和测量元件过程中有些系统的时滞量是不可避免的。前人也研究了相关的分数阶时滞混沌系统的同步问题。但是,由于数值仿真验证分数阶时滞微分混沌系统的稳定性不是那么容易。因此,相关的研究不是很多。
针对上述出现的问题,本文利用自适应模糊滑模控制研究了一类带有外界干扰和不确定项的分数阶时滞系统。最后通过数值仿真验证控制器的鲁棒性以及控制方法的有效性。
1 预备知识
1.1 分数阶微分算子定义
与经典的“整数阶”方法相比,分数阶微积分可以更准确地描述和建模实际对象。分数阶微积分目前没有统一的定义方法,但是常用的有3种。分别是:G-L型定义、R-L定义以及Caputo定义。在实际工程应用中,常用的是Caputo定义。因此,我们简单介绍Caputo定义。
其中,Caputo微积分拉普拉斯变换为
(2)
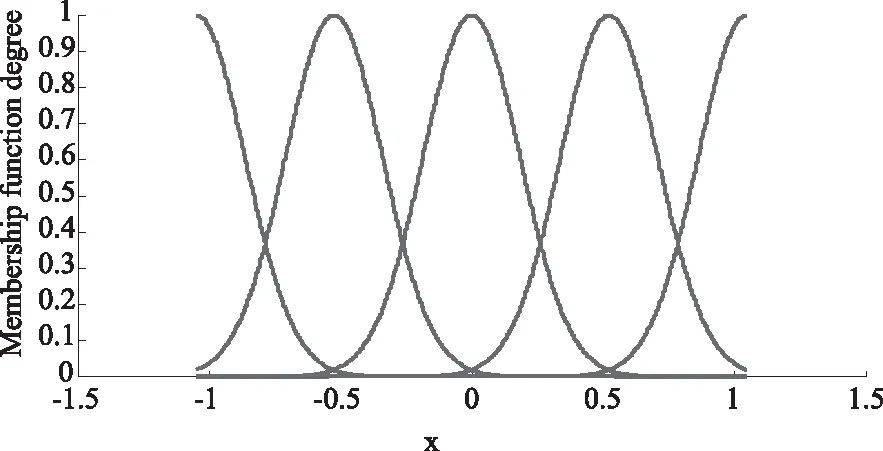
其中,m-1 计算分数阶微积分时,利用分数阶微积分的性质可以起到简化计算步骤的作用。因此,这里简单介绍常用的分数阶微积分的相关性质。 性质1:如果q=m,其中m是整数。那么此时,分数阶微积分的运算与整数阶m微积分运算相同。 性质2:如果q=0,那么aDtqf(t)=f(t) (3) 性质3: Dq[αf(t)+βg(t)]=αDqf(t)+βDqg(t) (4) DqD-q=D0f(t)=f(t) 性质4:分数阶微积分满足分配运算: Dtqf(t)=Dtq1Dtq2...Dtqnf(t) (5) 其中,q=q1+q2+...+qn 引理1:分数阶时滞微分方程为 (6) 其中,v(t)∈R,t∈[0,+∞)是非负连续函数。φ(t)≥0,t∈[-τ,0],满足-a+b<0则方程的零解是渐近稳定的。 设有一个二维模糊系统g(x)为集合U=[α1,β1]×[α2,β2]⊂R2上的一个函数,但是这个函数的形式是未知的.设对∀x∈U,都可以得到g(x),那么就可以设计一个逼近的模糊系统。那么就有下面的万能逼近原理:假设f(x)为构造的二维模糊系统,g(x)是未知函数。如果g(x)在U=[α1,β1]×[α2,β2]⊂R2是连续可微,那么模糊系统的逼近精度为 (7) 利用模糊系统的万能逼近特性,可实现对被控对象的模型信息和外界干扰的逼近,并能够通过参数自适应调整,实现不要模型信息的自适应模糊滑模控制。 考虑如下带有一类带有双重不确定项[15]的分数阶时滞系统。 其中,驱动系统为 (8) 响应系统为 (9) 其中,xi(t)(i=1,2,3,4)和yi(t)(i=1,2,3,4)为状态向量,τ为时滞量。f(x,t)、g(y,t)为该系统的非线性未知有界函数。d(t)为外界不确定项。u(t)∈R是控制输入。 当α=0.95,系统处于混沌状态。 同步误差可定义为 e(t)=(e1,e2,e3),其中ei(t)=yi(t)-xi(t),i=1,2,3。 首先,通过滑模到达条件,利用滑模变结构控制设计传统意义上的控制器[16],分两个阶段完成。第一阶段:系统状态由任意初始状态向滑模面运动,直到进入该平面。该阶段中滑模面对应方程不为0,此时设计的任务是使系统满足到达条件。第二阶段:系统状态进入滑模面并沿着滑模面运动。在该阶段si(t)=0,此时设计的任务是使滑模动态具有期望的性能。因此,文章将滑模控制器的设计分成了两个步骤:(1)进行切换函数的s(t)设计;(2)根据滑动模态的到达条件进行控制器的设计。 设计分数阶滑模面s(t),并在系统到达滑模面时满足条件s(t)=0。并且,保证系统误差e能够从第一阶段到达第二阶段的充分条件为 (10) 假设外界非线性函数f(x,t)、g(y,t)已知,并且无外界干扰,即d(t)=0。 定理1 误差系统的滑模面可设计为 s(t)=k1e1(t)+k2e2(t)+k3e3(t) (11) 其中,k1、k2、k3为任意常数,此时,驱动系统与响应系统达到同步状态。 Dqs(t)=Dq[k1e1(t)+k2e2(t)+k3e3(t)] =k1Dq(y1-x1)+k2Dq(y2-x2)+k3Dq(y3-x3) =k1(y2-x2)+k2(y3-x3)+k3[g(y,t)- f(x,t)+ueq(t)+e3(t-τ)] =k1e2+k2e3+k3[g(y,t)-f(x,t)+ueq(t)+ e3(t-τ)] =0 从而得到等价控制器 (12) 从而设计切换控制器 usw=ηswDq-1(sgn(s(t)) (13) 其中,ηsw为正常数,且满足:ηsw>|D1-qd(t)|+|D1-qω|,ω为最小近似误差估计值。达到克服和补偿系统的建模误差,以此保证系统的输出和状态是有界的。 因此,在非线性函数已知,并且不含外界干扰项仅有时滞量时,设计如下控制器,式(14)可使得误差系统趋于稳定,进而使驱动系统(8)与响应系统(9)达到同步。 e3(t-τ)-ηswDq-1(sgn(s(t)) (14) 然而在实际工程应用中,不仅含有时滞量一种影响系统稳定的因素[17]。除此,不可避免地存在外界干扰和未知不确定项。因此,实现驱动系统(8)和响应系统(9)同步,仅仅依靠控制器式(14)是远不够的。 (15) 引理2:如果基于模糊控制系统的间接自适应律为 (16) 其中,r1和r2为正常数。那么控制器保证了系统的全局稳定性,同步误差e(t)将渐近收敛到零。 定理2:根据传统滑模控制器(14)和模糊控制系统(15)得到自适应模糊滑模控制器为 e3(t-τ)-ηswDq-1(sgn(s(t)) (17) 使得带有不确定项以及外界干扰的分数阶混沌系统(8)和(9)逐渐同步。 (18) 其中,参数矩阵误差的定义为 接着,构造Lyapunov函数为 (19) 对式(19)求导,得 由式(11)得 Dqs(t)=Dq[k1e1(t)+k2e2(t)+k3e3(t)] =k1e2+k2e3+k3[g(y,t)-f(x,t)+u(t)+ d(t)+e3(t-τ)] 将式(17)代入: Dqs(t)=k1e2+k2e3+k3{[g(y,t)-f(x,t)]+ (sgn(s(t))]+d(t)+e3(t-τ)]} 由式(18)可得 -k3[ηswDq-1(sgn(s(t))]-d(t)-ω] (sgn(s(t))]-d(t)-ω] 由引理2以及不等式性质可以得出 =-k3|s(t)|{ηsw-‖D1-qd(t)‖-‖D1-qω‖}<0 即证。 因此,Lyapunov稳定性定理可知,双重不确定分数阶混沌误差系统,在控制器(14)的作用下,逐步稳定。不仅实现了驱动系统(8)与响应系统(9)的快速同步,在T-S模糊控制系统作用下,也有效地削弱了抖振。 考虑如下被控对象: (20) 系统阶数q取值为0.97;参数k1=k2=k3=1,正常数r1=r2=h=0.001,其中,h为步长。选取系统初值为x(0)=[0.2,0.6,0.9],y(0)=[0.1,0.5,0.3];时滞量τ=1;切换参数ηsw=2.5,选取以下5个为模糊输入的隶属函数。 μNM(xi)=exp[-((xi+π/3)/(π/12))2] μNS(xi)=exp[-((xi+π/6)/(π/12))2] μZ(xi)=exp[-(xi/(π/12))2] μPS(xi)=exp[-((xi-π/6)/(π/12))2] μPM(xi)=exp[-((xi-π/3)/(π/12))2] 其中,隶属函数图如图1所示。 图1 隶属函数图 通过Matlab数值仿真[20]得到传统意义下的不确定分数阶时滞混沌系统的仿真结果,即图2和图3。 图2 误差系统时间历程 图3 传统控制器时间历程 通过图2观察到,在运行前期误差系统的同步效果,当时间t=4 s时,误差系统e1达到同步;时间t=2 s时,误差系统e2、e3逐步趋于同步。 通过图3可以观察到控制输入前期阶段,由于切换项的引入引起了抖振现象,直至时间t=5 s时,系统逐渐稳定。 因为滑模变结构控制中,切换增益项的引入引起系统抖振,这无论从理论上还是实际工程上都会带来一些应用的困难。理论上,切换增益函数为不连续函数,因此势必会使得对应工程模型方程的解不是唯一的。工程应用上,控制器的抖振会造成执行结构的过度消耗。因此,对传统的控制器通过模糊控制系统进行改进,其仿真图效果如图4和图5。 图4 误差系统时间历程 通过图4,观察到误差系统通过对控制器改进之后,其很好地达到了同步状态。 图5 改进控制器时间历程 通过图5,可以观察到控制器在运行到时间t=2 s时便已经逐渐稳定。很好地达到了削弱抖振的效果。 基于Lyapunov稳定性分析方法,研究了具有干扰的两个不确定分数阶时滞混沌系统之间的混沌同步问题。建立了T-S模糊控制系统模型作为改进的逼近器,对不确定项和未知参数进行了近似。建立了自适应滑模控制系统,提出了自适应滑模控制设计方法,不仅保证了所提出控制方法的稳定性和鲁棒性,也可以确保同步误差的外部干扰得以缓解。最后,仿真结果表明了该控制策略的适用性和有效性。1.2 分数阶微积分性质
1.3 模糊系统的万能逼近原理
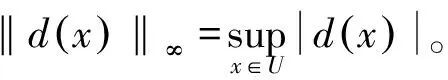
2 系统的描述
3 控制器的设计
3.1 滑模变结构控制器的设计
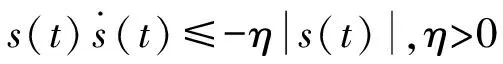
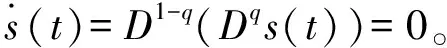
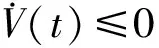
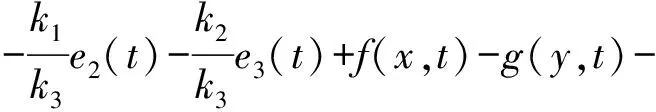
3.2 自适应模糊滑模控制器的设计
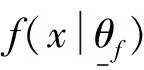
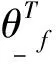
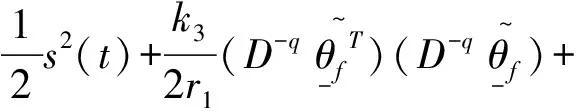
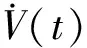
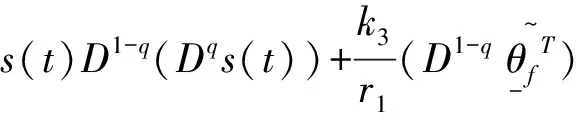
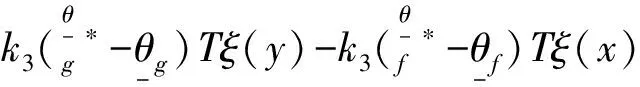
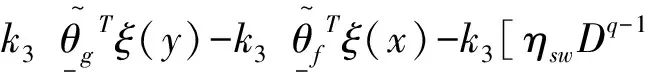
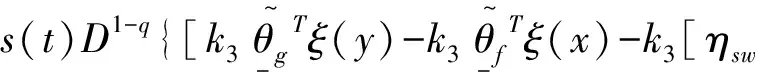
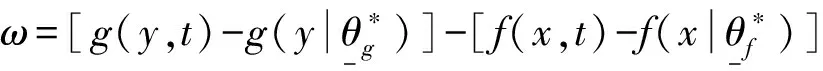
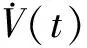
4 数值仿真

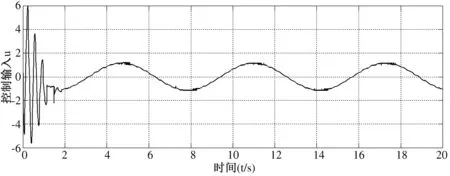
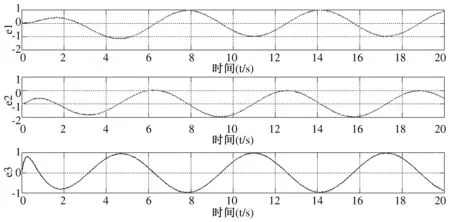
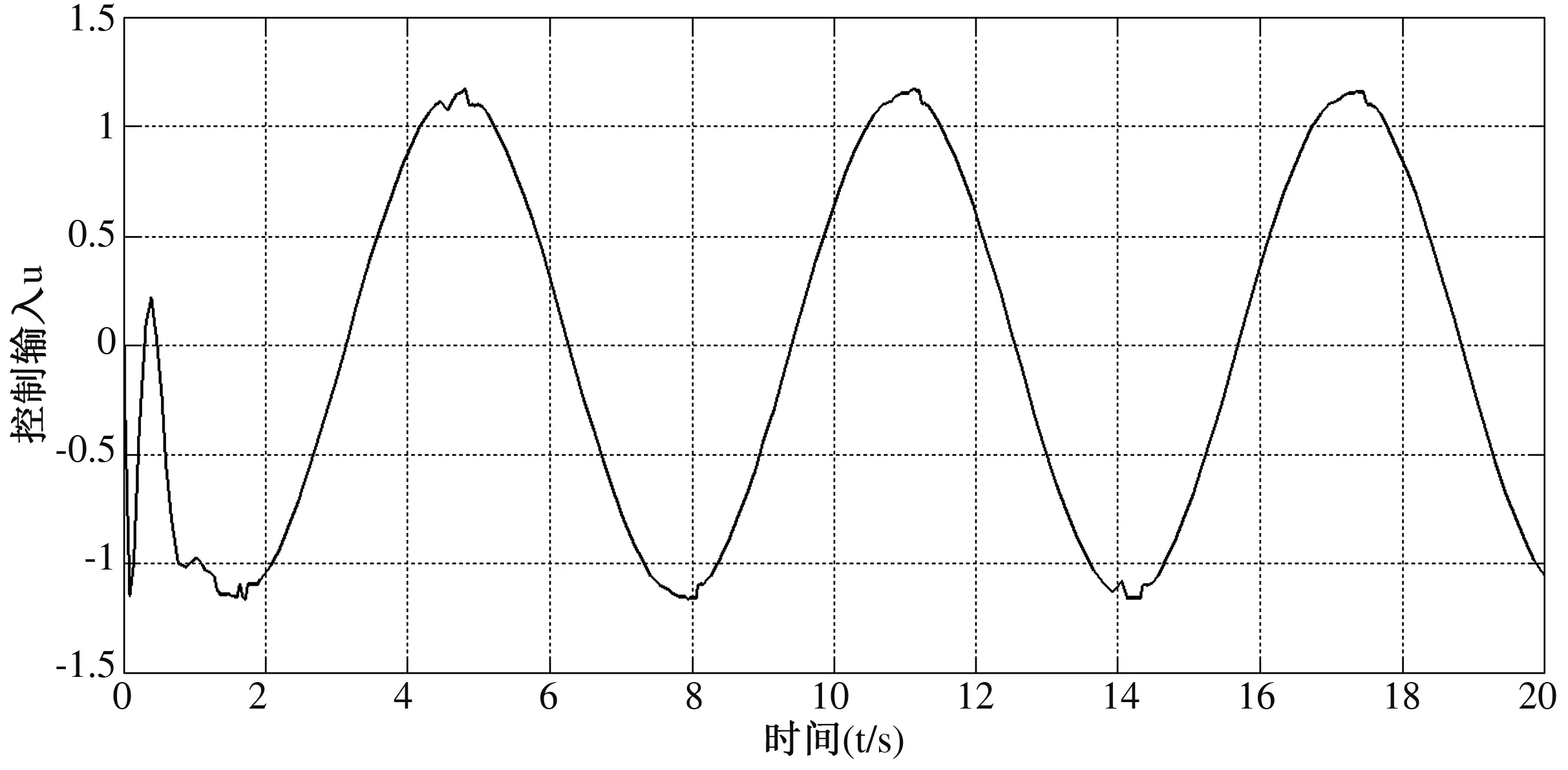
5 结论
