机器人焊接圆柱相贯线中心定位的解析方法

盖晓华， 郭学军， 王喜平， 刘增磊， 刘登第

(1.南阳理工学院智能制造学院 河南 南阳 473000;2.南阳理工学院数理学院 河南南阳 473000;3.空军指挥学院作战仿真研究所 北京 100097)

0 引言

目前自动化焊接中的机器人焊接大多采用的是寻迹焊接。由于焊接工件、材质及焊缝宽窄深浅的不同使得焊缝中心轨迹的准确确定非常困难。在焊缝的特征点确定以后，如何根据焊接工件焊缝的固有特征和特征点的坐标确定焊缝中心是非常重要的[1]。郭学军等给出了圆形焊缝三维空间中心位置的确定方法，可通过修改控制软件的程序及参数来调节焊接设备的功能，实现圆形、半圆形、分段多段圆弧、环形焊缝的焊接，但所研究的焊缝是基于平面圆的[1]。苗新刚等采用了基于相贯线变形普遍规律的椭圆拟合法和基于曲线拟合的三坐标轴分立最小二乘法方法进行焊缝轨迹拟合，椭圆拟合法是针对圆及椭圆形问题，三坐标轴分立最小二乘法由于分离环节的增加容易造成系统误差[2]。汪苏等的相贯线焊接机器人示教再现的工程化实现方法是在骑座式焊接机器人环境下进行轨迹拟合和寻迹焊接的，适应范围有一定的局限性[3]。汪苏、曾翠华等提出了基于弗莱纳-雪列的轨迹规划方法，虽然有效解决了复杂空间曲线位置和姿态控制，但求解过程复杂、计算量大，导致轨迹规划的难度加大[4-6]。本文根据机器人焊接双目摄像定位原理，利用最小二乘法，以圆柱面相交所形成的三维曲线中心轨迹的确定为例，给出了空间三维曲线型焊缝中心轨迹确定的一般方法。

1 系统标定

目前机器人焊接的摄像系统有单目和双目之分[7-9]，大多采用的是双目摄像系统，因为双目摄像系统能较为准确地测定特征点的坐标。双目摄像系统通常有3个坐标系，两个摄像镜头所确定的坐标系以及被测对象所在的世界坐标系，通过摄像机的标定可以将3个坐标系以及被测的对象有机地联系在一起。设定摄像机内外参数、双目视觉关系、机器人手-眼关系、机器人手-工具关系均预先标定[10，11]。如图1是本文采用的双目机器人焊接示意图。

图1 机器人焊接双目摄像定位示意图

已知焊接工件焊缝的形状为空间曲线，其投影为圆形线。将焊缝工件的投影圆心通过世界坐标系的z轴并且使焊件投影圆环所在的平面与z轴垂直，焊枪也与工件所在的切平面垂直。激光扫描仪对焊缝作垂直扫描，通过双目摄像系统的标定可以得到焊缝的一些检测点，再通过滤噪处理可得到最小区域的特征点Mi(xi,yi,zi)，i=1,2,,…,n。根据特征点可确定出空间焊缝的方程。然后，通过编程，上位机指示焊枪沿曲线方程所确定的轨迹进行焊接。

2 直径相等正相交圆柱焊缝中心轨迹

2.1 相贯线模型及焊缝轨迹确定原则

设两直径相等圆柱正相交，如图2所示，其相贯线方程为

(1)

(1)式中两式相减可得

y=±z

则相贯线的参数方程为

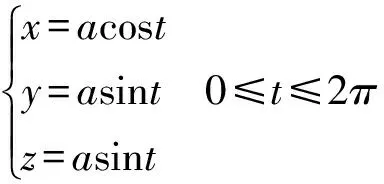
(2)

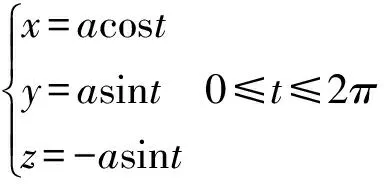
(3)

其正投影为圆形，符合本文系统标定所规定的条件，可用文献[1]的符号标定方法。

图2 两直径相等圆柱正相交示意图

2.2 焊缝轨迹的确定

特征点到焊缝的距离di的确定方法。设Mi(xi,yi,zi)为焊缝一特征点，M1(x1,y1,z1)为中心轨迹l上一点，且M1(x1,y1,z1)是Mi(xi,yi,zi)与曲线l上所有点的连线中长度最小的连线点，即MiM1是Mi到曲线l的距离。

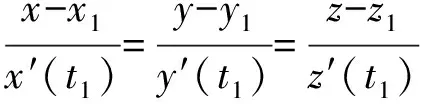
(4)

切线m1的方向向量为

直线MiM1的方向向量为

由于m1垂直于MiM1，

故有

(xi-acost1)×(-asint1)+(yi-asint1)×(acost1)+(zi-asint1)×(acost1)=0

(5)

化简得

(6)

设s=sint1，则(6)式化为

(7)

利用MATLAB可求s与xi,yi,zi的关系。不妨设s=s(xi,yi,zi)，则M1(x1,y1,z1)坐标形式有两种

z1=as(xi,yi,zi,a),

即M1亦有两种表示，分别设为M11、M12

则di=min(MiM11,MiM12)，不妨设di=MiM11

则有

M1=M11

(yi-as(xi,yi,zi,a))2+(zi-as(xi,yi,zi,a))2

(8)

其和为

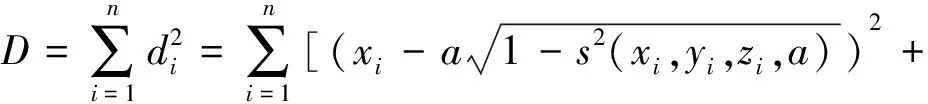
(yi-as(xi,yi,zi,a))2+(zi-as(xi,yi,zi,a))2]

(9)

可得依据特征点所确定的焊缝中心轨迹为

(10)

图3 两直径为2 m圆柱正相交仿真图

2.3 实例验证

有两个半径为2 m，壁厚为2 cm的正相交圆柱形工件，其仿真图像如图3所示，其相贯线如图4所示。根据相贯线轨迹已对两圆柱进行相应的切割，现需要对接起来进行焊接。

（3）连续性。根据开发生产资料、操作成本和评估日油价等，每年要定期进行两次剩余经济可采储量评估，并将评估结果正式对投资者披露。

图4 两直径为2 m圆柱正相交交线仿真图

表1 焊缝坡口的特征点坐标

采用“一”字条形结构光-激光，对焊缝作垂直扫描。同时双目机器人摄像系统读取包含有“一”字形光源特征的焊缝，根据双目视觉系统的三角测量原理和图像处理技术，利用光条特征——激光条的对应变形，来匹配变形光条的拐点，三维检测点确定以后，再经过滤波处理得到了焊缝坡口的特征点，如表1所示。

依据表1特征点的三维坐标，利用本文所给出的解析定位方法，求得参数a=2.0136，即焊缝中心轨迹方程为

(11)

其相应的仿真图形如图5所示。这与事前拟定值a=2，焊缝工件切割时的半径相比较其绝对误差Δa=0.0136。可以看出精确度较高，从而说明这种焊缝轨迹中心线的拟合方法是切实可行的。

图5 特征点及焊缝中心轨迹仿真图

3 不相等正相交圆柱焊缝中心轨迹

3.1 相贯线模型及焊缝轨迹确定

设两直径不相等的圆柱正相交，其相贯线方程为

(12)

(12)式中两式相减可得

y2-z2=a2-b2

则相贯线的参数方程为

(13)

(14)

其正投影为圆形，仍符合系统标定所规定的条件，现以(13)式为例说明焊缝轨迹的确定方法。与直径相等的正相交圆柱确定方法类同，按照第2部分相关表示，则有

M1点的切线m1的方向向量为

化简得，

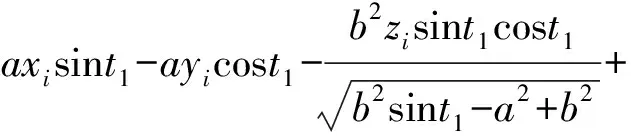
(b2+ab-a2)sint1cost1=0

(15)

设s=sint1，则(6)式化为

利用MATLAB可求s与xi,yi,zi的关系，不妨设s=s(xi,yi,zi,a,b)，与等柱体相似可求得

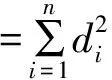
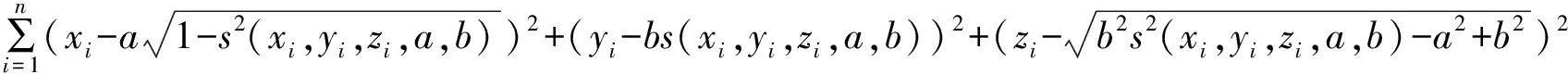
(16)

(17)

可求得a,b与xi,yi,zi的关系a=a(xi,yi,zi)、b=b(xi,yi,zi)，即可求得焊缝中心轨迹

(18)

3.2 实例验证

有两个半径分别为2 m和3 m，壁厚均为2 cm的正相交圆柱形工件，其仿真图像如图6所示，其相贯线如图7所示。根据相贯轨迹已对两圆柱进行相应的切割，需要对接起来进行焊接。测得焊缝的特征点如表2所示。

依据表2特征点的三维坐标，利用本文所给出的解析定位方法，求得参数a=2.0217，b=2.9328，

即焊缝中心轨迹方程为

(19)

其相应的图形如图8所示。这与事前拟定值，焊缝工件切割时的半径a=2、b=3相比较其绝对误差,Δa=0.0217，Δb=0.0072，精确度较高。

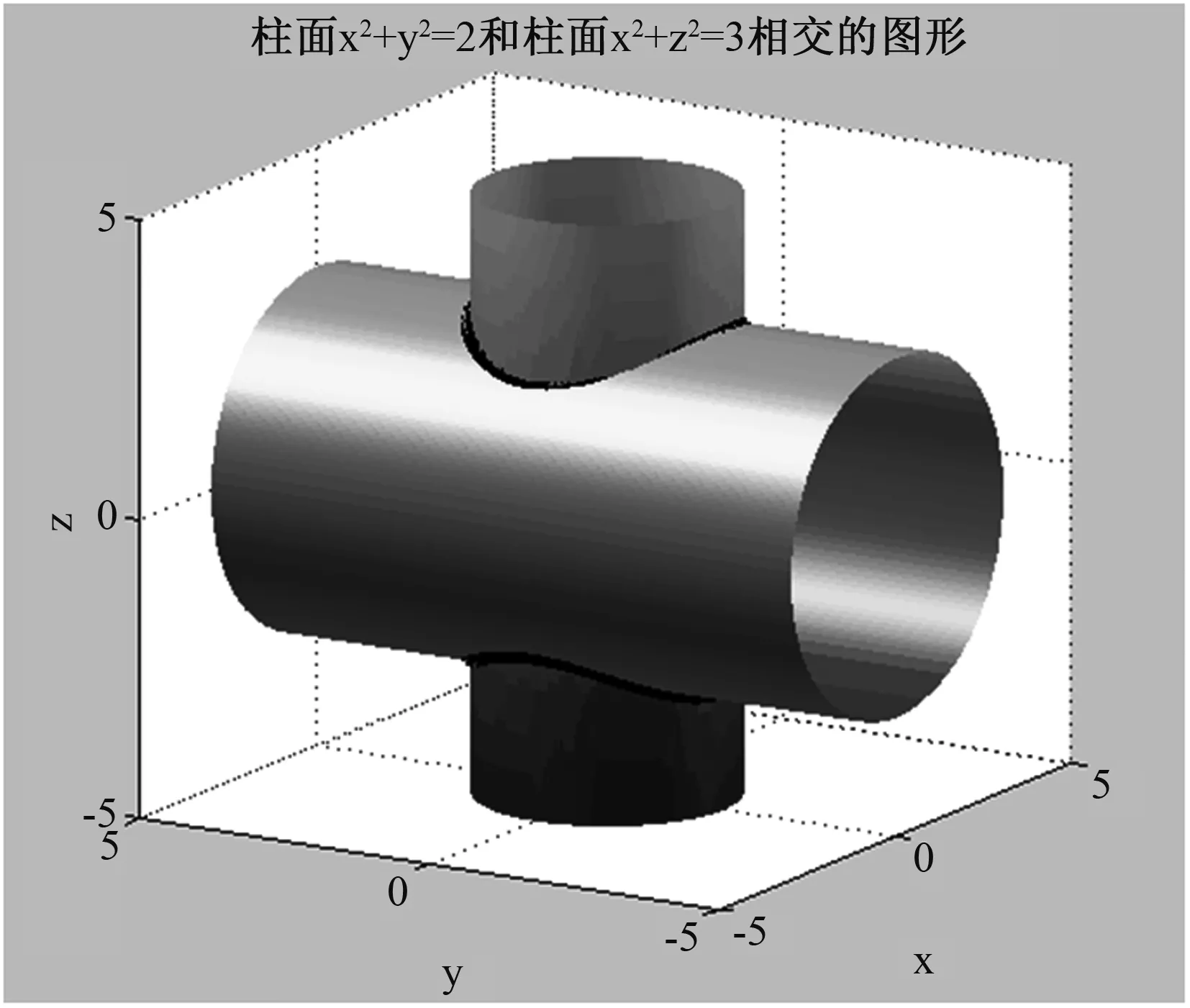
图6 两个半径分别为2 m和3 m的圆柱正相交

图7 柱径不等正交圆柱交线仿真图

表2 柱径不等焊缝坡口的特征点坐标

图8 柱径不等特征点及焊缝中心轨迹仿真图

4 结论

本文探讨了直交圆柱相贯线焊缝中心轨迹的定位方法。实例表明，这种依据特征点坐标确定空间焊缝三维曲线中心轨迹的方法，实用可靠，对同类问题的解决具有一定启发意义。关于利用本文所给出的空间曲线形焊缝中心定位的解析方法进一步解决圆柱斜交问题及相近的相贯线问题，还有待于进一步探讨。