基于IDA的异形柱框架剪力墙地震易损性分析

2021-02-28钟岱辉田擎

山东建筑大学学报 2021年1期

钟岱辉田擎

(山东建筑大学土木工程学院，山东济南250101)

0 引言

异形柱框架—剪力墙结构(以下简称异形柱框剪结构)因其可以保证建筑物内部平整美观且可增加建筑有效使用面积，目前已在多、高层建筑中得到广泛应用，但这一结构形式也存在着应用时间短、经历地震检验少且缺乏实际的震害数据等缺点。因此，对该结构抗震性能评估多采用试验方法或有限元分析方法[1]。由于地震具有很强的随机性和不确定性，上述传统分析方法仅考虑特定地震动参数输入下的结构性能。从统计学概率分布角度评估结构的抗震性能，其准确性应该更高[2]。

增量动力分析IDA(Incremental Dynamic Analysis)是一种基于弹塑性时程分析的参数化分析方法，通过对结构进行大量地震波不同强度幅值下的动力时程分析，为结构的抗震性能分析提供广泛而全面的数据。建筑结构的地震易损性分析，描述了在不同强度地震下结构处于各性能水准的概率分布。IDA可为结构的地震易损性分析提供必要的数据，两者结合则对结构在地震作用下可能发生的损坏作出全面而准确的评估，因此备受广大研究人员的重视:吕西林等[3]提出了复杂高层结构基于增量动力分析的地震易损性分析方法；张令心等[4]采用IDA方法对1栋50层的混合结构抗震性能做了分析，证明结构具有良好的抗震性能；万赞[5]采用IDA方法分析了三榀型钢异形柱框架的抗震性能，确定了结构的最弱失效模式。此外，还有许多研究人员基于IDA方法做了大量研究[6-8]。

但是，直至目前，尚未形成适用于钢筋混凝土异形柱框剪结构的地震易损性分析方法。因此，文章在定义相关极限状态的基础上，提出了基于IDA的地震易损性异形柱框剪结构分析方法，以1栋11层异形柱框剪结构为例进行了分析，从概率角度评估其抗震性能，并借助性能评估软件PBSD(Performance-Based Seismic Design)统计了罕遇地震下结构主要构件的损坏等级及位置，可作为大震下结构性能评估的补充和完善。

1 异形柱框剪结构地震易损性分析方法概述

IDA是一种涵盖结构从弹性变形到弹塑性变形再到倒塌的全过程分析方法，本质上是一种动力推覆分析。相较于传统静力推覆分析，IDA方法计算的是结构在地震作用下的动力响应过程，因而可以较好地克服其由于将动力过程简化为静力过程而带来的诸多问题[9]。目前，IDA方法已广泛应用于结构抗震能力分析和性能评估中，如美国联邦紧急救援署在FEMA-350中将该方法用于分析钢框架抗倒塌能力极限[10]。地震易损性分析描述的是结构在各强度地震下达到或超过某种极限状态LS(Limit State)的条件概率，可由易损性曲线或易损性矩阵表示[3]。传统地震易损性矩阵的建立一般通过震害调查来完成，但对于应用时间较短的某些结构，其震害资料匮乏，因而传统方法具有很大的局限性。相比之下，通过IDA获取结构性能数据的方法更为可行。研究结合已有成果，提出了异形柱框剪结构基于IDA的地震易损性分析方法，其步骤如下:

(1)准确建立非线性分析模型。

(2)选取一系列能代表结构所在场地地震危险性的地震动记录，采用适当的调幅方法[11]以及合适的地震动强度指标IM(Intensity Measure)和结构损坏指标DM(Damage Measure)。

(3)计算每条地震波不同幅值下结构的动力响应，并将结果绘制成IDA曲线。

(4)定义极限状态LS，量化与结构损坏指标间的关系，得到由结构损坏指标表示的极限状态；计算不同地震动强度下，结构响应超过某极限状态LSi的概率，即P(LSi｜IM＝im)。假设LSi通过DM量化为dmi，当IM＝im时，DM超过dmi的概率由式(1)表示为

文献[12]证明了DM对IM的条件概率服从对数正态分布，由式(2)表示为

式中μlnDM｜IM＝im和σlnDM｜IM＝im分别为IM＝im时，DM的对数均值和对数标准差；Φ(·)为标准正态累积分布函数。

(5)以IM为横轴，P(LSi｜IM＝im)为纵轴，绘制各极限状态下的地震易损性曲线。

(6)根据易损性分析结果，结合GB 50011—2010《建筑抗震设计规范》[13]规定的不同水准地震对应的地面运动强度指标，计算结构超越各极限状态的条件概率。

2 异形柱框剪结构易损性分析

2.1 算例简介

算例为1栋11层高的异形柱框架—剪力墙住宅。底层层高为3.6 m，其上各层均为3 m、结构总高度为33.6 m，总建筑面积为2 891.3 m2。结构平面布置如图1所示。抗震设防烈度为7度，地震设计分组第一组，场地类别为Ⅱ类，场地特征周期为0.35 s，抗震设防类别为丙类。结构中使用的L形柱、T形柱均为等肢长柱，肢长为800 mm、肢厚为200 mm；剪力墙长边为1 600 mm、短边为800 mm，其厚度与柱肢相同。混凝土强度等级除异形柱为C35外，均为C30，钢筋强度等级均为HRB400。

图1 结构平面布置图/mm

2.2 非线性分析模型的建立与检验

异形柱截面形式不规则，普通柱单元无法准确模拟其在地震作用下的非线性行为，因此使用地震抵抗设计的非线性软件PERFORM-3D中的纤维化单元对其进行模拟[14]。此外，PERFORM-3D强大的多线程计算功能可同时进行多条地震波下结构的弹塑性时程分析，从而提高了计算效率。

采用盈建科建筑结构计算软件YJK对结构配筋，并将配筋结果应用到非线性分析模型中；通过与YJK计算的动力特性相对比，检验非线性模型的准确性。其所建立的分析模型如图2所示。

图2 异形柱框剪结构模型图

PERFORM-3D计算的结构前3阶振型如图3所示。两软件计算的结构前6阶振型与自振周期见表1。由结果可知，YJK与PERFORM-3D计算的自振周期偏差均≤6%，验证了非线性模型的准确性。

图3 结构前3阶振型图

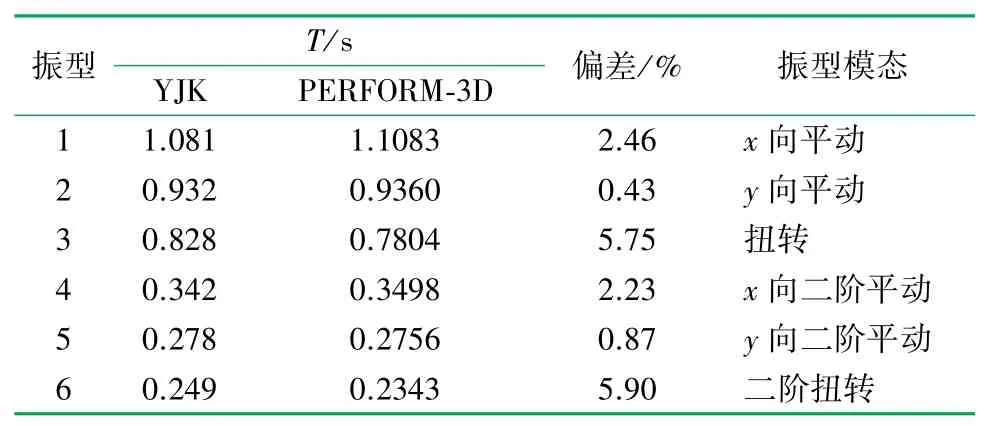
表1 结构自振周期对比表

2.3 地震波选取

DBJ/T 15-151—2019《建筑工程混凝土结构抗震性能设计规程》[15]中，所选取的地震动参数应能反映结构所在场地最大地震规模、震中距和震源机制，优先选用本场地或附近场地记录的地震波，也可选择与场地地质条件相似的场地记录的地震波，地震波持续时间不得小于建筑结构基本自振周期的5倍或15 s。对于中高层结构，选取10～20条地震波即可满足分析所需精度[16]。基于上述原则，从美国太平洋地震中心PEER地震波库中选出10条与结构场地地质条件相似的地震波，见表2。其中，g为重力加速度，cm/s2；PGA(Peak Ground Acceleration)为峰值地面加速度，×g；PGV(Peak Ground Velocity)为峰值地面速度，cm/s。

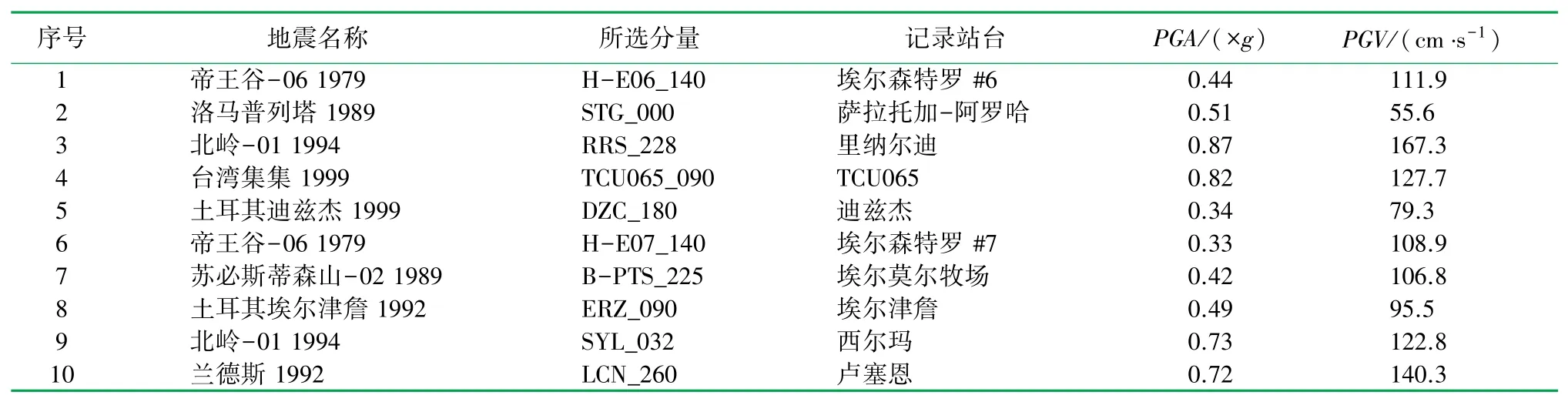
表2 所用地震波表

2.4 相关指标选取

常用地震动强度指标IM有峰值地面速度PGV、峰值地面加速度PGA及阻尼比为5%的结构基本自振周期对应的谱加速度Sa(T1，5%)等，为充分考虑高阶振型对结构所受地震作用的影响[17]，选择PGA作为地震动强度指标。常用结构损坏指标DM有结构顶点位移、最大层间位移、最大层间位移角等。其中，最大层间位移角θmax与结构整体损伤、构件破坏、抗倒塌能力联系紧密，因此选择θmax作为结构损坏程度指标。

2.5 结构极限状态的定义

结构性能水准的临界状态称为极限状态。吕西林等[3]对高层混合结构定义了5个性能水准和极限状态，并提出了相应的层间位移角限值，见表3。

研究参照吕西林定义的极限状态[3]，结合异形柱框剪结构的特点，做出如下调整:异形柱结构最大适用高度＜150 m，因此仅保留结构高度＜150 m时的极限状态；混合结构中钢框架的延性优于RC框剪结构中钢筋混凝土框架，因此参照JGJ 149—2017《混凝土异形柱结构技术规程》[18]中关于混凝土异形柱框架结构弹塑性位移角限值的规定，将接近倒塌水准下的层间位移角限值由1/33调整为1/50。由此得到异形柱框剪结构的性能水准和极限状态，见表4。

表3 高层混合结构极限状态层间位移角限值表

表4 异形柱框剪结构极限状态定义表

2.6 地震易损性分析

x方向为结构刚度的薄弱方向，因此按照x∶y为1∶0.85的方式输入地震波。调幅后各地震波PGA值分别为0.05g、0.1g、0.3g、0.5g、0.7g、0.8g、0.9g、1.0g，之后根据结果判定继续调幅或终止计算。计算完成后将结果绘制成IDA曲线，如图4所示。

结合IDA结果，通过式(2)计算各极限状态的超越概率。以极限状态LS1为例，其层间位移角限值为1/800，计算不同PGA取值时对应的θmax对数均值μlnθmax｜PGA和对数标准差σlnθmax｜PGA，带入式(3)计算θmax超过1/800的概率为

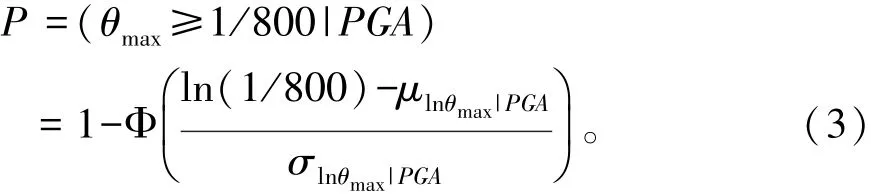
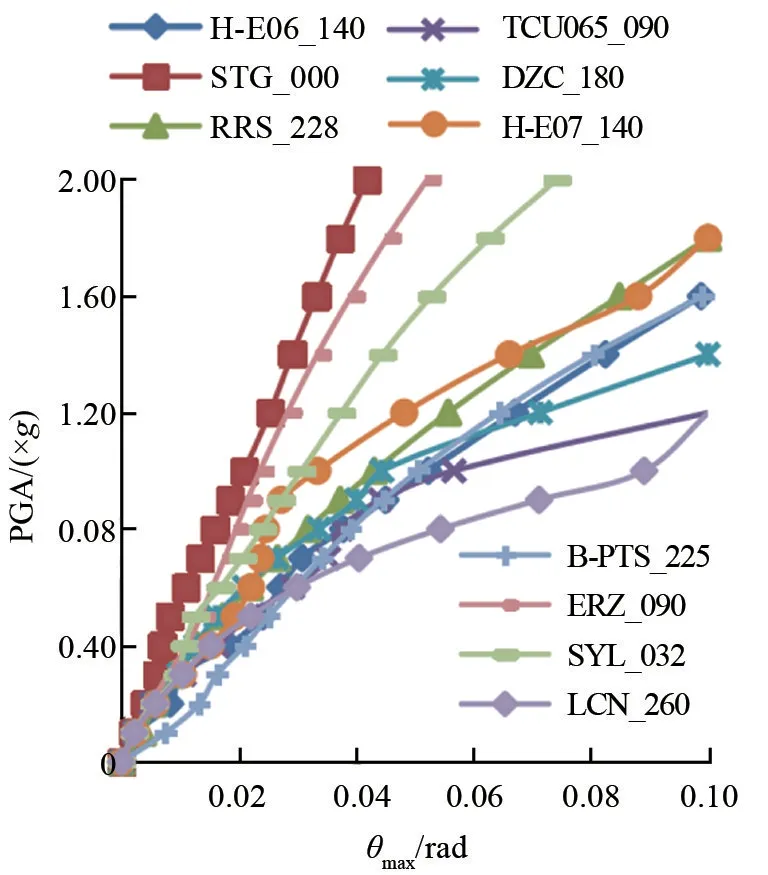
图4 IDA曲线簇图

计算完成后，以PGA为横轴，P(θmax≥1/800｜PGA)为纵轴绘制极限状态LS1下的结构超越概率曲线。类似的，可绘制出其他极限状态下结构的超越概率曲线，如图5所示。

GB 50011—2010[13]中7度多遇、设防及罕遇地震对应的PGA峰值分别为0.036g、0.100g及0.224g。由图5可得3个地震水准对应的超越概率，见表5。表5即是常见的地震易损性矩阵，表示了结构最大层间位移超过某一极限状态的概率。为了直观表示结构处于某性能水准下的概率，对其进行转化，以7度多遇地震为例简述其过程。

7度多遇地震下，结构正常使用的概率为100%-21.29%＝78.71%；基本可使用的概率为100%-2.68%-78.71%＝18.61%；修复后使用的概率为100%-0.06%-78.71%-18.61%＝2.62%；生命安全的概率为100%-0%-78.71%-18.61%-2.62%＝0.06%；接近倒塌的概率为100%-0%-78.71%-18.61%-2.62%-0.06%＝0%。同理，可得其他水准地震下结构处于各性能水准的概率，见表6。

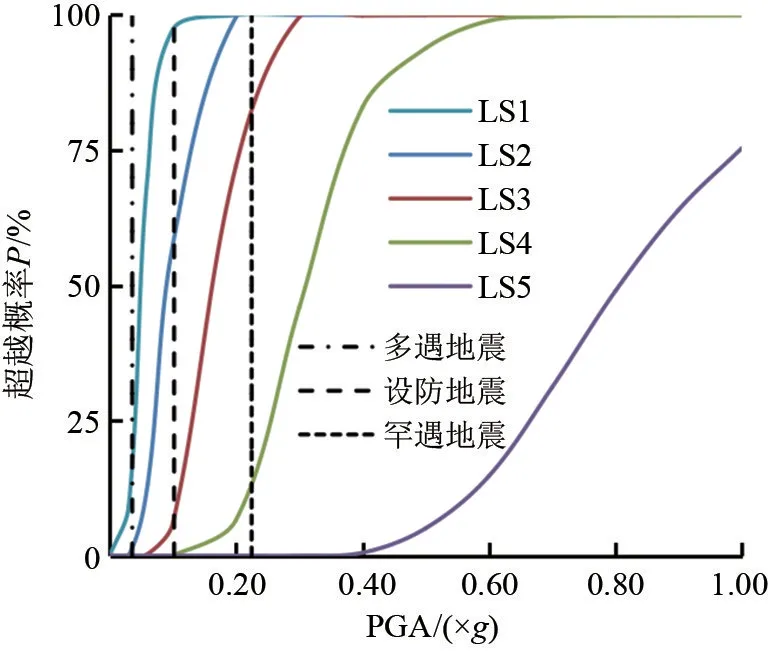
图5 结构各极限状态对应的超越概率曲线图

性能状态正常使用可对应于GB 50011—2010[13]中的设防目标“不坏”，基本可使用、修复后使用对应于“可修”，生命安全对应于“不倒”。由表6可知，该异形柱框剪结构小震不坏的概率为78.71%、中震可修的概率为93.98%，大震不倒的概率为83.96%，基本能满足规范提出的设防目标，结构整体具有良好的抗震性能。

表5 异形柱框剪结构各极限状态对应的超越概率表

表6 异形柱框剪结构处于各性能水准的概率表

3 大震下构件性能状态研究

地震易损性分析可从宏观角度评价地震下结构发生损坏的程度及概率，但是并未体现结构构件的损伤情况，然而结构关键构件的损坏程度及位置也是评估结构抗震性能的重要因素。因此，借助结构性能评估软件PBSD对结构关键构件在7度罕遇地震作用下的最大损坏情况做了统计。

软件采用DBJ/T 15—151—2019[15]的标准，以材料应变为依据划分了构件的性能状态，划分标准见表7。7度罕遇地震下结构梁、柱、墙构件损坏等级及分布如图6所示。

表7 材料应变对应构件性能状态表

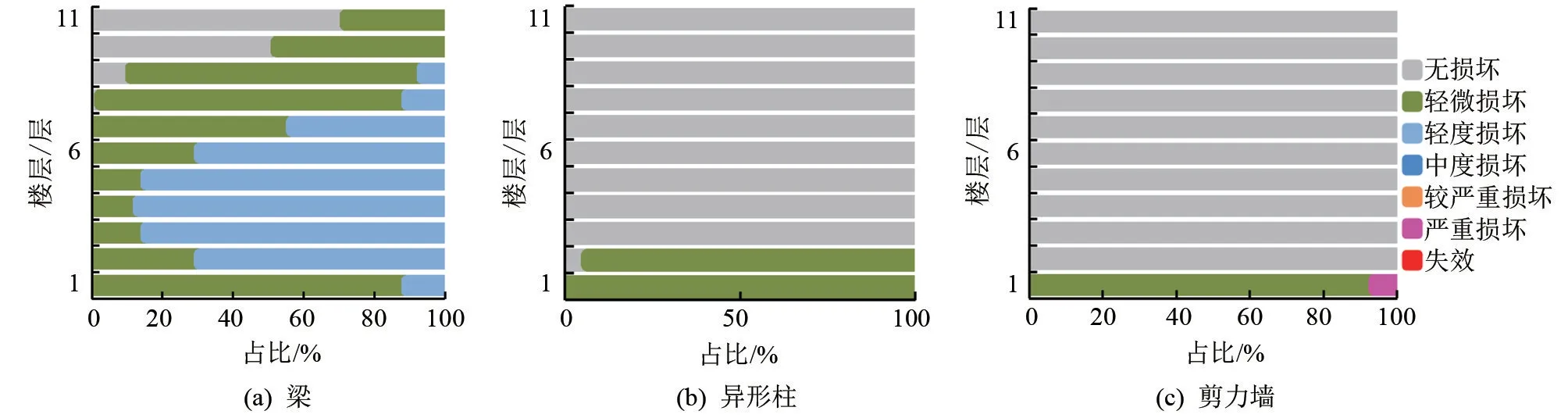
图6 主要构件损坏等级及分布图

由图6可知，7度罕遇地震下＞80%的梁构件已发生损坏，损坏程度多为轻微损坏及轻度损坏，其中3～5层梁损坏程度较其他楼层更加严重；约17%的柱构件损坏，多为轻微损坏，主要集中在1～2层；约9%的剪力墙构件损坏，以轻微损坏为主，但有极少数(＜1%)发生了严重破坏，集中在第1层。梁作为主要耗能构件出现了大面积损伤，承担了地震耗能的作用，符合了“强柱弱梁”的设计初衷；与梁相比，柱和墙所受损害较轻，但是存在少数剪力墙发生了严重损坏，因此结构设计时应对底层墙构件采取适当的加强措施。从构件损坏分布来看，结构具有良好的延性及耗能能力，抗震性能优良。