盾构开挖对邻近桩基影响的试验研究

魏焕卫奎耀罗威孔军杨帆

(1.山东建筑大学 土木工程学院，山东 济南250101；2.济南轨道交通集团有限公司，山东 济南250000)

0 引言

随着城市化进程的不断加快，城市地下空间的利用在缓解交通压力方面起着越来越重要的作用。在修建地铁时，由于施工对周围土体产生的扰动而影响了临近环境，当邻近桩基础受到扰动时桩身会产生附加的应力和位移，从而对桩基承载力造成不利的影响。

针对盾构开挖对临近桩基受力影响的研究方法主要有数值计算和模型试验法。李早等[1]在CHEN等[2]两阶段分析方法基础上，利用数值计算首先求解出土体自由位移场，再将位移施加于桩体上，对比了桩身受力数据与有限元的计算结果。杨晓杰等[3]通过有限差分法，结合广州地铁施工中的工程实例，研究了隧道修建引起临近桩基的承载力变化规律。吴全立等[4]利用Abaqus二维有限元数值模拟方法，分析了盾构开挖所形成的盾壳环向间隙填充效应对既有线隧道沉降的控制作用。朱逢斌等[5]利用离心机试验与数值模拟结果进行对比，研究了隧道开挖对群桩内力变化规律的影响，验证了数值计算方法的可靠性。徐林[6]利用模型试验与数值模拟相结合的研究方法，分析不同影响因素对建筑物桩基础的影响变化规律。马少坤等[7]和邵羽等[8]利用水袋排水法模拟隧道开挖进程，在离心机模型中展开了对于临近桩基工作性状的研究。孙雷江[9]和朱逢斌[10]利用自主研发的隧道模型进行试验，研究隧道临近既有深基坑和临近多层框架结构时构筑物的内力。利用模型试验对盾构施工的研究较为广泛，与数值模拟比较起来具有方便直观的优势。

虽然已经有多位学者研究了隧道施工对临近桩基础的影响，但是针对桩周土体压力变化对桩身受力影响方面的研究较少。文章利用模型试验的方法，分析了桩长不同时与隧道距离不同时的桩身受力情况，并从桩侧土压力差值变化的方向研究了其对桩身的受力变化规律。

1 材料与方法

利用自主研制的可控地层损失率的隧道模型进行了缩尺模型试验，重点研究隧道与桩基的不同距离对桩基础的桩身附加弯矩、附加轴力以及桩顶竖向位移值的影响。

1.1 材料选取及模型尺寸

试验在尺寸为1.1 m×0.9 m×1.2 m的模型箱内进行，模型箱整体利用10 mm厚的钢板与角钢焊接而成，其中一面采用半封闭式设计，方便放置隧道模型以及操作模型试验装置。试验土样采用福建厦门标准砂，密度为1 505 kg/m3；通过直剪试验所得内摩擦角为40.47°，内粘聚力为零。模型试验示意图如图1所示，其中桩与隧道距离以B表示。

图1 模型试验示意图/mm

隧道采用自制的试验模型，缩尺比例为1∶40，直径为150 mm，选取材料为无 规 共 聚 聚 丙 烯PP-R(Polypropylene Random)管材，取部分管体试验材料进行拉伸试验，根据试验数据的应力—应变曲线可得隧道模型弹性模量为3.44 GPa。试验中桩基础模型采用4根单桩与承台组合而成，定义靠近隧道一侧的桩体为前桩，远离隧道的桩体为后桩，桩体材料采用内径为13 mm、外径为15 mm的聚氯乙烯PVC(Polyvinyl Chloride)管材制作，承台采用成品PVC板材切割成120 mm×120 mm尺寸进行模拟。4根桩分别按照距承台边界20 mm距离安置在承台上，相邻两根桩间距为80 mm，连接处采用钢丝进行绑扎并且涂抹改型丙烯酸酯胶进行粘结，隧道埋深等数据将在试验布置中详细介绍。试验模型如图2所示。

图2 试验模型成品图

1.2 试验布置及设计方案

将应变片粘贴在模型桩桩身测量附加弯矩和附加轴力，模型桩桩长为45 cm。距桩头顶部60 mm处开始布置第一个应变片，应变片粘贴间隔为70 mm，底部距离40 mm处为最后一个应变片，如图2(b)所示；桩长为35 mm时，第一个应变片距顶端30 mm，粘贴间隔为60 mm。在模型桩基础承台上方4个角点处布置百分表，每15 min读一次数，直至稳定，以观测承台表面侧向位移和桩顶竖向位移值。

填充砂体阶段，将砂体倒入模型箱内至放置模型隧道位置处，每铺设100 mm厚砂层则进行人工击实，然后添置下一层的砂土。隧道模型位置固定完毕后，对桩基模型进行定位，并安设支架方便放入模型。待按照设计位置安置好隧道模型和群桩模型后，继续填放砂体直至350 mm覆土厚度，隧道底面埋深为45 cm。承台上部设置80 mm×80 mm的方形平板，采用放置砝码的方式进行加载，放置砝码重量为10 kg，施加于桩基础的荷载约为1.5 kPa。试验流程如图3所示。试验方案共分为6种情况，其中方案1、2和3中桩长不变，仅改变桩基与隧道间隔的距离B(如图1所示)，方案4、5和6中改变桩身长度为35 cm，但是与隧道距离对应保持不变。具体试验方案见表1。

图3 模型试验流程图

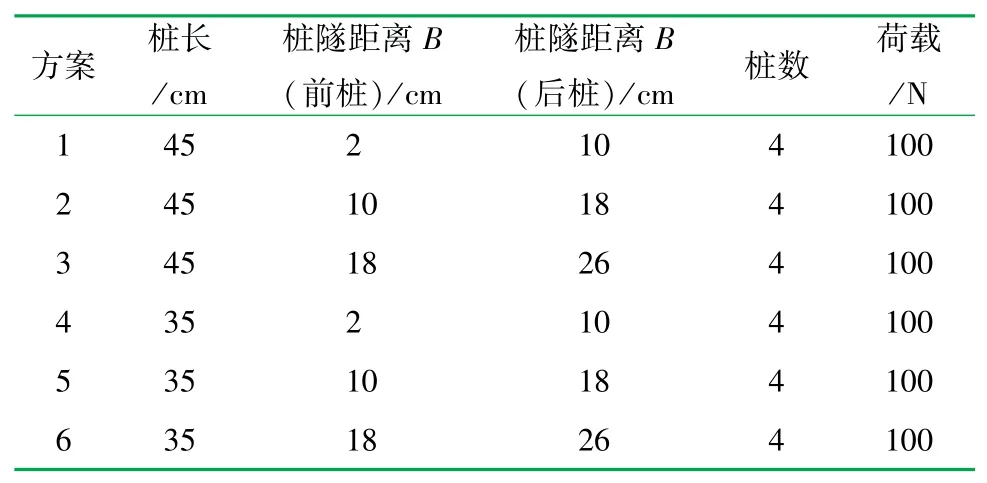
表1 不同桩长和桩隧距的试验方案表

1.3 试验研究内容

试验利用自制隧道模型装置进行土体损失过程的模拟，忽略具体施工过程的影响，仅考虑隧道施工过程中实际开挖土体体积以及竣工后隧道体积之差[11]，考虑到缩尺模型试验现象的局限性，试验设计土体损失比率为5%，待砂体填埋完成后静置24 h，至土体基本稳定开始进行试验。

自制试验模型通过内壳空隙设置与外壳空隙设置错落布置，在隧道模型机关开合的情况下模拟土体损失的情况。试验开始后，将通过操作预留在模型箱外的抽拉装置控制周围土体产生的土体损失。土体损失量则由放置在隧道模型内的隔离环进行控制，可以通过隔离环的大小进行不同土体损失率的试验。

2 结果与分析

2.1 地表沉降及桩基位移分析

2.1.1 地表土体沉降值

通过控制隧道模型装置内衬大小控制隧道开挖产生的土体损失率，利用表面架设位移计记录5%和10%两种不同损失率的土体沉降值并进行对比。将两种地层损失率利用文献[12]中的公式进行线性拟合，依据土体损失率并结合隧道开挖半径R推出地面沉降槽宽度系数i，由式(1)和(2)表示为

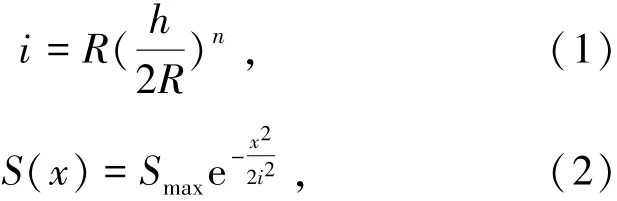
式中R为隧道开挖半径，m；h为隧道埋置深度，m；n为经验系数，取0.8～1.0；S(x)为地面任意一点的沉降值，mm；Smax为地表沉降最大值，mm；x为从沉降曲线中心到计算点的距离，m。

通过式(2)计算可以得出距离隧道中心点不同位置处的沉降值大小。将Peck公式拟合值、实测值和数值计算值进行比较分析，其对比曲线如图4所示，采用试验方法所测得沉降槽曲线与Peck公式曲线基本吻合。Peck公式计算所得地表沉降最大值为10.0 mm，实测沉降曲线成高斯分布，数值计算最大沉降值为8.26 mm，比实测值结果小，但计算所得的沉降槽曲线与试验结果一致。通过试验现象侧面证明了模拟隧道开挖引起地层损失的影响可以利用试验方法和数值模拟为依据进行精准的还原。

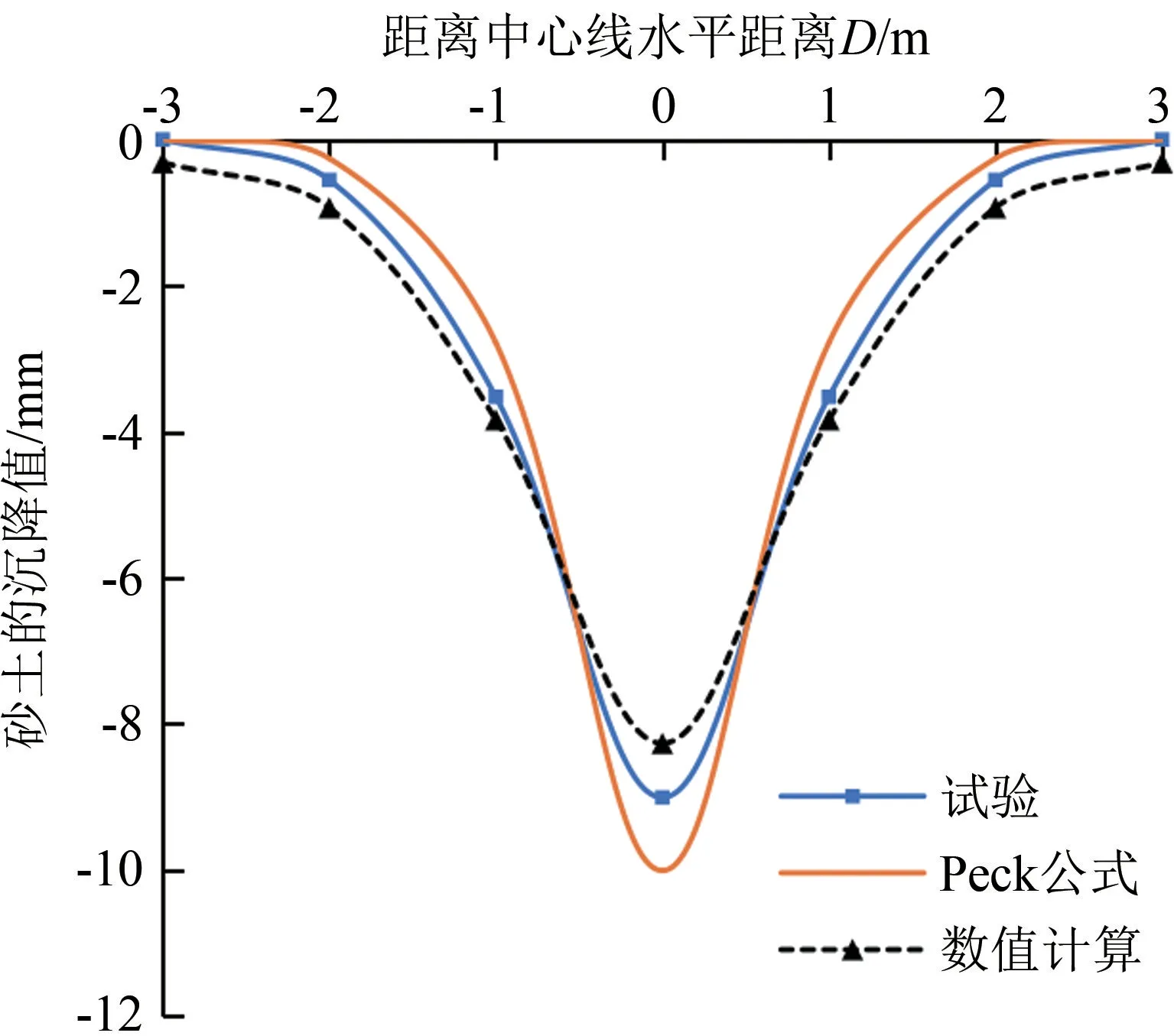
图4 地表土体沉降对比曲线图

2.1.2 桩基顶部竖向位移

利用位移计记录桩基础顶部竖向位移(见表2)。通过分析可知，桩长为45 cm时的桩基顶部倾斜率和桩顶竖向位移值远小于桩长35 cm的桩基顶部倾斜率和桩顶竖向位移值。隧道开挖后，土体位移场因土体损失的原因发生改变，桩侧土体产生松弛导致靠近隧道侧土压力减少，桩周土体发生相对向下的位移。桩长为45 cm时，由于桩侧土体产生了竖向位移，从而导致了桩侧摩阻力的减少和桩端阻力增加，桩顶部分产生了较小的沉降值；桩长为35 cm时，桩身侧摩阻力同样减少，同时由于桩底埋深位于隧道顶部埋深平齐位置，隧道开挖产生的土层位移导致了桩端地层的压缩模量减少，导致桩端阻力由于应力松弛的原因也减小，小于桩长为45 cm时的桩身承载力，所以桩长35 cm时产生的桩顶沉降大于桩长45 cm时的桩顶沉降。

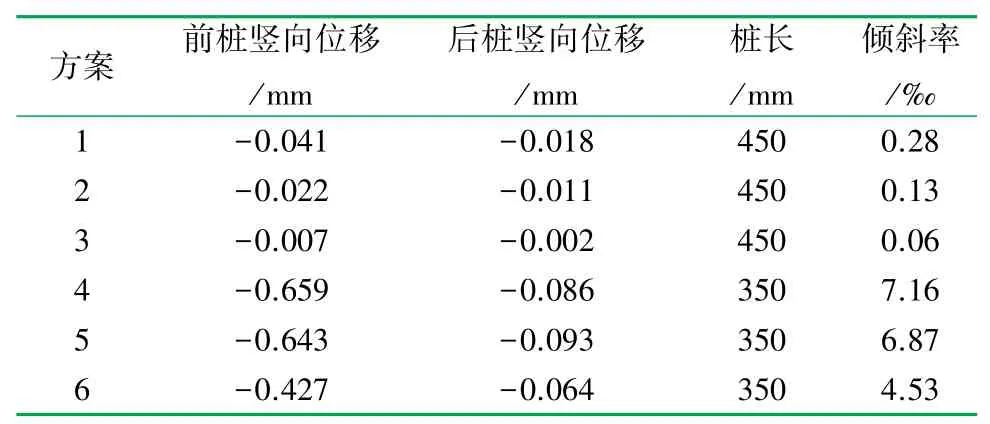
表2 不同试验方案的桩顶竖向位移表

前排桩顶部竖向沉降值均大于后排桩，且倾斜率随隧道距离的增加而减小，最大倾斜率达到7.16‰，其原因在于前排桩的存在导致后排桩侧土体位移减小，桩身侧摩阻力和端阻力并未产生较大改变。

2.2 桩身内力分析

2.2.1 桩长45 cm时不同桩隧距的桩身弯矩

桩长45 cm时不同距离的前桩和后桩弯矩曲线如图5所示。试验中以桩身临近隧道处一侧受拉为正，将不同方案的前桩与后桩的弯矩值进行对比分析。由图5(a)可以看出，距离隧道越近桩身所受最大弯矩值越大，方案1的弯矩最大值为12.85 N·m，并且最大值位置处距离隧道埋深处越近。其原因在于靠近隧道较近，隧道开挖产生的土体损失导致桩身靠近隧道一侧土体产生位移，距离隧道位置越近处土体位移越大，桩身两侧土压力的不平衡导致了附加弯矩值的增大[13]。

从数据上看，桩端靠近承台位置区域弯矩值呈现较明显的负值，其原因在于承台下方土体由于隧道开挖产生的位移带动桩身产生了变形，而且承台与桩体连接处为刚结，所以因抵抗桩体向隧道侧移产生了负弯矩区域。

方案1和2在桩体埋深为10～30 cm区域内都产生了较大的正弯矩，而方案3正弯矩出现在＞20 cm的区域内，随着与隧道的距离越远桩身正弯矩区域逐渐向桩体顶端移动。3个不同试验情况下的桩身底部均出现了较为明显的负弯矩，由于桩身上部受土压力不平衡而导致的位移较大，但桩身下部则相对受土体位移影响较小，反而因桩端嵌固作用提供给桩身以抵抗位移的反力，从受力上看呈现了负弯矩的情况。

由图5(b)可以看出，由其规律同前桩弯矩大致相同。但是相同位置处后桩弯矩值低于前桩弯矩值，后桩由于前桩对周围土体发生运动所做的抵抗，隧道开挖引起的土体位移在后桩位置处会减小，这种减小作用称之为桩基的遮拦作用[14]。正因遮拦作用的存在，减弱了靠近隧道侧土体土压力的变化，导致两侧土压力变化差值减小，从而附加弯矩值变化也随之减少。方案3中后桩距离隧道最远，所以其弯矩值也最小，同样由桩身两侧土压力不平衡，距离隧道越远处桩产生正弯矩区域越向上移。

桩长45 cm时相同距离的前后桩弯矩对比如图6所示，可以更为明显地观测出由于前桩的遮拦作用的影响减小了桩两侧压力不平衡现象。对比方案1和2中距离隧道10 cm的前桩与后桩，可以看出前桩弯矩最大值相较于后桩更大，最大值所处位置也略低于后桩，并且除去桩端顶部之下直至桩身30 cm处弯矩值大致呈现正值。

图5 桩长45 cm不同距离前桩和后桩弯矩曲线图

2.2.2 桩长35 cm时不同桩隧距的桩身弯矩

桩长35 cm时不同距离前桩和后桩弯曲矩对比曲线如图7所示。根据图7(a)所示的方案4、5和6的前桩桩身弯矩分析可知，其弯矩图与桩长45 cm的变化规律大致相同。距离隧道越近处弯矩值越大，且正弯矩区域随距离隧道越远位置向桩顶端移动。前桩与桩长45 cm的试验现象不同的是附加弯矩值负值区域较少，其原因在于桩端埋置深度与隧道顶部持平，桩底受土体位移场影响较大。距离隧道2、10 cm处，桩长35、45 cm的桩身弯矩最大值范围大致相同，并且整体趋势相近，所以在靠近隧道一定区域内，土体位移对于桩身的影响范围相同。

观察桩长35 cm的后排桩不同距离的弯矩数据，可以得出类似规律，如图7(b)所示，距离隧道越近受土体位移场的影响程度较大，但由于前桩的遮拦作用使产生的附加弯矩值相对较小。

图6 桩长45 cm相同距离前后桩弯矩对比曲线图

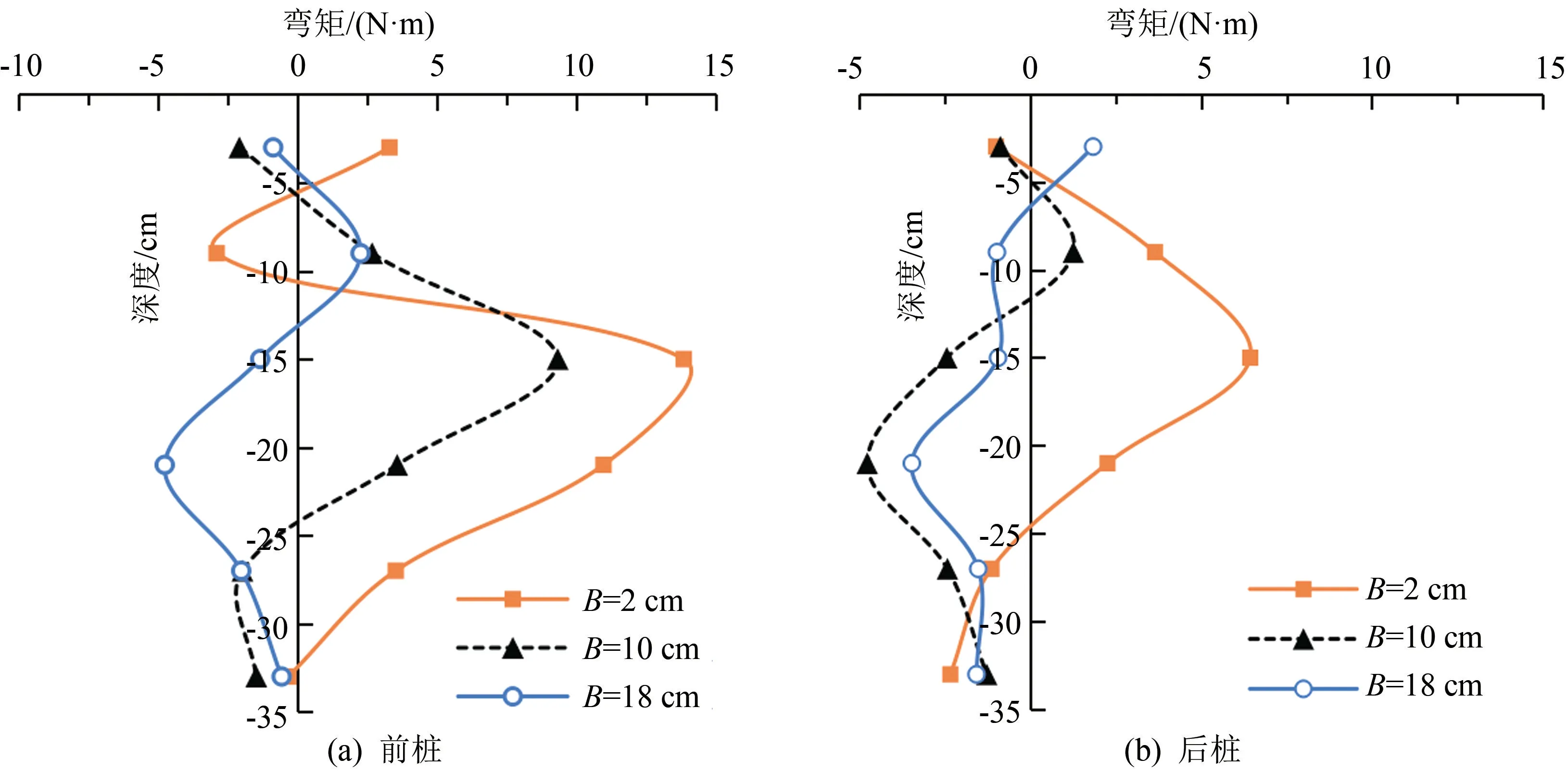
图7 桩长35 cm不同距离前桩和后桩弯矩对比曲线图

将方案4中的后桩与方案5中的前桩弯矩值进行对比，可以明显观测出前桩的隔离作用。桩长35 cm相同距离的前后桩弯矩对比如图8所示，后桩弯矩值相较前桩更小，并且与桩长45 cm的试验数据得出的规律大致相同。试验表明，不同桩长的前排桩遮拦效应都较为明显，且在弯矩数据中表现出遮挡作用一致的现象。与距离隧道10 cm位置处前后桩的弯矩曲线相比较，距离隧道18 cm的前后桩的弯矩值较小，且弯矩变化趋势不明显，但是后桩的弯矩值大小依然略小于前桩，可以看出桩身较短时距离隧道一定范围外的前桩隔离效果比桩身较长时的情况要小。

2.2.3 桩身附加轴力影响分析

对于不同试验的桩身轴力数据，在室内试验中很难准确测定，而数值模拟的方法可以获得模型中桩身任意点的轴力数据及其他参数，并且经对比试验实测值后验证了其可行性和可靠性，故利用数值计算的结果对隧道开挖引起临近桩基的桩身附加轴力进行分析。桩长45 cm不同距离前桩和后桩轴力对比曲线如图9所示。

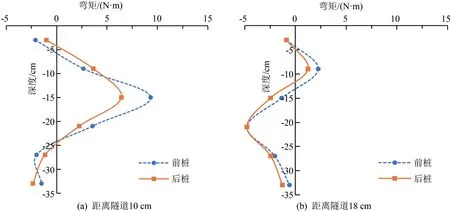
图8 桩长35 cm相同距离前后桩弯矩对比曲线图

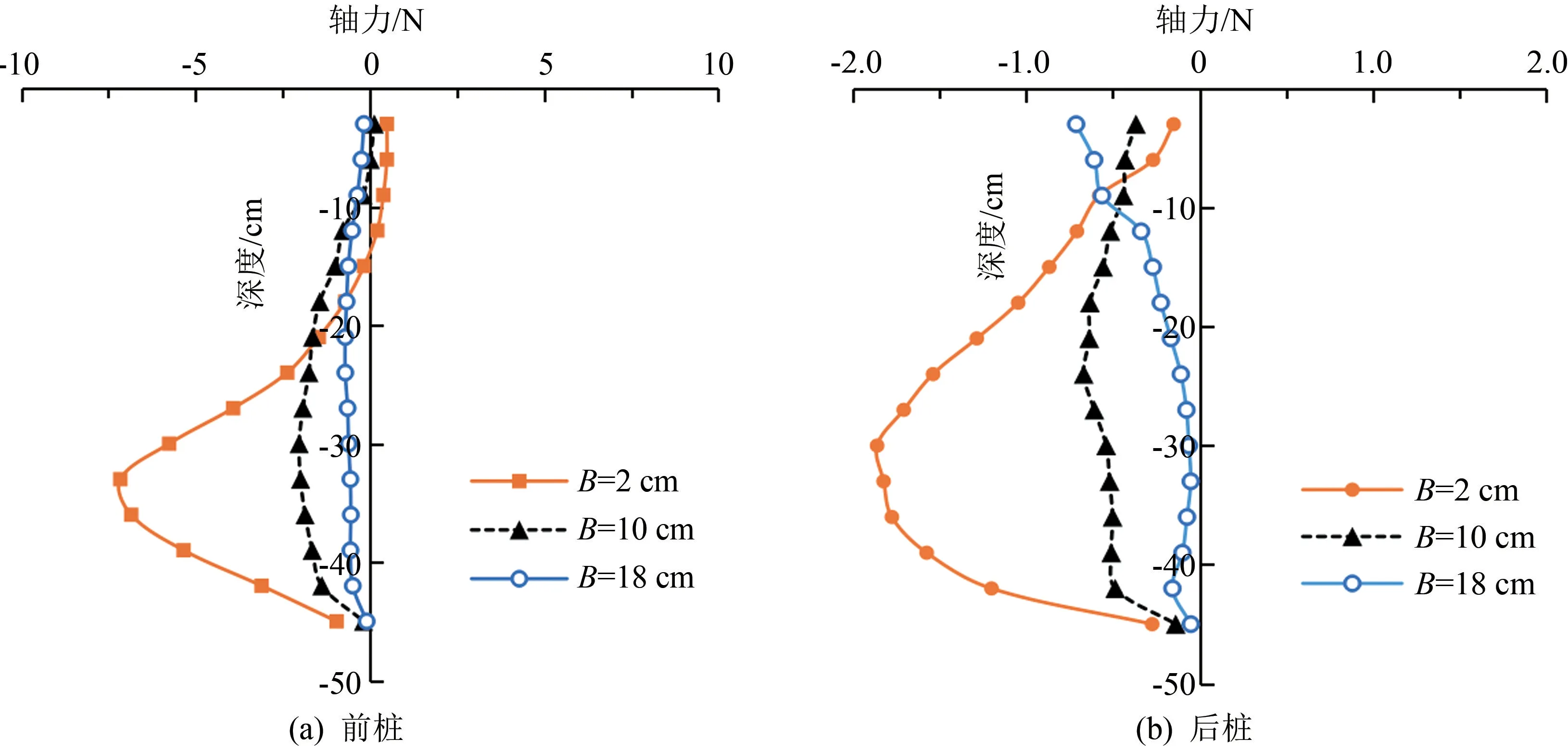
图9 桩长45 cm不同距离前桩和后桩轴力对比曲线图

由图9(a)所示的前桩的桩身轴力可知，方案1中轴力增大程度最大，距离隧道越远的桩体轴力增大程度越小。其轴力增大的原因为:隧道开挖导致的土体损失导致桩身周围土体发生位移，土体位移方向相对于桩身向下，桩侧阻力减小并产生一定程度的负摩阻力[15]，从而使桩端轴力增加，桩身轴力呈现增大的现象。随着距离隧道越来越远，桩身周围土体所受隧道开挖导致位移场改变的影响变小，桩周土体相对沉降量减少，从而桩侧阻力减小值越来越小，因桩端阻力增加而增大的轴力值也较小。

观测后排桩随不同距离变化的附加轴力值，如图9(b)所示，可以发现整体数值较前桩明显减小，整体规律与前桩较为类似。因为前桩的遮拦作用使得土体损失产生的地层沉降值减少，前桩的桩身阻力阻隔了土体向下的位移，所以后桩的轴力增大值相较前桩减少。

3 结论

采用了模型试验和数值模拟的方法研究了隧道开挖引起的临近桩基础影响，观测了不同桩隧距离下桩身的附加弯矩和附加轴力变化，得到以下主要结论:

(1)模型试验和数值模拟得出的地表沉降数据与Peck公式拟合值相吻合，并且桩基顶部竖向位移和倾斜率距离隧道越远数值越小，桩基础的桩身越短受隧道开挖的影响越明显。

(2)桩身附加弯矩受土体位移导致的桩身两侧土压力不平衡影响较大，并且随隧道距离的增加影响减小，由于前排桩的遮拦效应导致后排桩受影响效果减弱。且在不同桩长的情况下，附加弯矩受影响规律大致相同，距离隧道越远正弯矩区域越靠近顶端，但相比之下桩长较长时，其受桩端下部嵌固作用影响较大，桩身会出现负弯矩区域更大。

(3)桩身附加轴力受土体竖向位移影响较大，因为桩侧阻力的减小导致桩端阻力的增加，桩身轴力变化整体趋势为轴力增加，后桩由于前桩的隔离作用桩身附加轴力增加较小。