基于时间富余度控制的滑行道调度优化模型
2021-02-27姜雨童楚刘振宇胡志韬徐成张洪海
姜雨,童楚,刘振宇,胡志韬,徐成,张洪海
(1.南京航空航天大学,民航学院,南京211106;2.航空电子无线电研究所,上海200241)
0 引言
大型繁忙机场跑道端与停机坪出入口区域内航空器滑行路径多有交叉,为冲突多发区域。航空器早于预定时间到达该区域容易造成排队累积,晚于预定时间到达该区域容易错过跑道端起飞时隙,导致航班不能按时起飞。因此,研究场面航空器到达滑行终点准时性的调度优化具有现实意义。
在大型机场航空器滑行调度方面,国内外学者主要从有向图建模与Petri 网建模方面开展研究。有向图模型采用图论方法将场面结构抽象化为“点-线”模型,通常结合混合整数规划进行建模。W.EISZER 等[1]构建路径集以简化调度,以最小化滑行耗时和燃油消耗为目标建立滑行道优化模型;YU C.等[2]采用基于最短路径的路径集简化模型,以有向图的方式进行机场场面建模,建立以油耗最小为目标的混合整数规划模型;姜雨等[3]联合考虑滑行道与停机位子系统间的相互作用机理,构建以滑行道调度和停机位指派为上、下层模型的双层规划模型。基于Petri 网的滑行道调度相对于有向图结合混合整数规划的建模方式起步较晚。PODGORSKI P.等[4]利用Petri网建立航空器动态路径选择模型,能够有效识别机场场面冲突热点区域;LUO X.等[5]基于构建的有向Petri 网,建立无冲突发生的场面资源调度优化模型。在模型求解方面,国内外学者大多采用智能算法。JUEPET J.等[6]提出顺序启发式算法,进行航空器滑行路径和跑道排序问题的联合求解,提高跑道效率的同时减少滑行时间;KAMILA B. K. B.等[7]采用蚁群算法寻求滑行总耗时最少的最优滑行路径;李善梅等[8]以优化进、离场航班的滑行路径为目标,提出基于变步长的滑动时间窗方法和A*算法相结合的模型求解算法,实现了对滑行冲突的智能识别与解脱。
纵观国内外研究现状,建模方式以有向图与Petri 网建模为主,仿真算法以智能算法为主,大多研究成果以优化滑行路径为主,最小化滑行时间、滑行距离或燃油消耗,通过优化算法结构提升模型求解效率。而航空器在机场场面滑行过程是连续过程,具有整体性,若不考虑航空器到达滑行终点的准时性,以缩短滑行时间,降低滑行成本为目标而进行路径优化,则会对后续跑道调度和停机位指派造成不可避免的影响。本文以提高航空器到达滑行终点的准时性为目标,建立基于时间富余度控制(Time Margin Control,TMC)的滑行道调度优化模型,使航空器到达滑行终点(跑道入口或停机坪入口)的时间尽可能契合预计到达时间,降低航空器到达误差,减少跑道端与停机位的排队等待;设计生物地理学算法(Biogeography- based Optimization,BBO)结合MATLAB进行仿真验证。
1 问题描述与建模
1.1 问题描述
大型机场进、离场航空器共同作用于跑道、滑行道和停机位资源系统。进、离场航空器之间相互影响,相互制约。尤其在滑行道运行部分,既要避免航空器滑行冲突,保障航空器滑行安全,又要保障航空器滑行的准时性,提高场面资源运行效率。因此,滑行道是航空器运行安全和运行效率的综合作用体。大型机场航空器场面运行过程如图1所示。

图1 进离场航空器场面运行过程Fig.1 Surface running process of approach and departure aircraft
1.2 模型假设
(1)研究时段内所有航空器滑行起讫点,开始滑行时间,预计结束滑行时间均为已知。
(2)机型决定航空器恒定的滑行速度。
(3)相邻的若干停机位被整合成1块停机坪,视为同1个节点,且停机位容量满足航空器调度需求。
(4)不考虑航空器加速起步和减速静止的过程。
1.3 模型建立
(1)目标函数
本文采用无向图G(V,E)进行大型机场场面网络建模,调度目标为最小化航空器总滑行时间和到达误差的加权和,目标函数为

式中:A、D分别为进、离场航空器集合;R为预设路径集合;Ri为航空器i的滑行路径,Ri∈R,Ri由节点vi排列构成,即Ri={vi,vi+1,…,vn} ,∃vn∈V,V为节点集合;sm,n为边(m,n)的空间距离,m,n为节点编号,(m,n)∈E,E为边的集合;n0为起始节点编号;Tni、Tn′i、Tmni分别为航空器i在节点n处为避免3 类滑行冲突产生的等待时间,其中,n∈V,(m,n)∈E,i∈A⋃D;t′i,d为航空器i实际到达终点的时刻;ti,d为航空器i预计到达滑行终点的时刻;ui为航空器i的滑行速度;η为到达误差的权重。
式(1)中航空器总滑行时间由航空器无冲突滑行时间和因冲突产生的等待时间构成,到达误差为实际完成滑行与预计完成滑行时间的偏差。当航空器提前到达,即t′i,d<ti,d时,η=1;当航空器发生延误,即t′i,d>ti,d时,η=2。
(2)约束条件
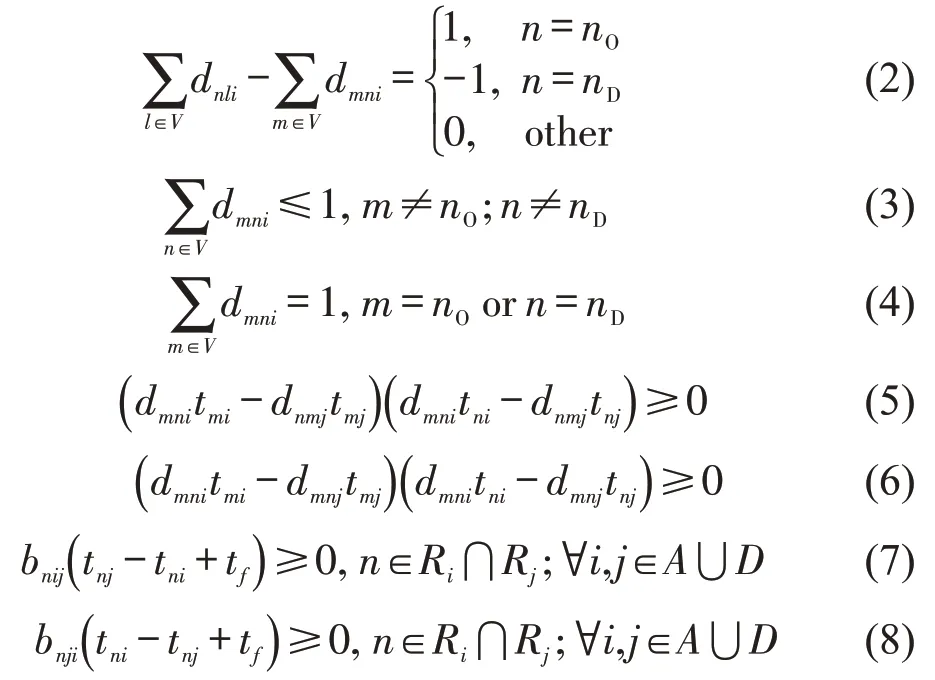
式中:dmni为0-1 决策变量,当航空器i依次由节点m至n通过边(m,n)时,其值为1,否则为0;l为路径节点编号;nO、nD分别为滑行路径起点、终点;tf为规定的最小安全间隔;tni为航空器i滑行至节点n的时刻;bnij为航空器i比航空器j先通过节点n。
式(2)~式(4)为滑行路径约束。式(3)和式(4)保障航空器在固定起、讫点且经过任意节点不超过一次的滑行路径。式(5)和式(6)分别表示避免航空器滑行的对头冲突(保证两相向航空器不同时处于同一链路)、超越冲突(保证同一链路上同向航空器满足安全间隔)。式(7)和式(8)表示避免航空器交叉点冲突(保证先后通过同一节点的两航空器满足安全间隔)。
1.4 优先级设立
解决滑行冲突的本质是确定两架航空器在通过冲突节点或滑行道链路的先后顺序。本文引入时间富余度的概念,为航空器设置的动态优先级为

式中:Ti(fy)为时间富余度,度量航空器i滑行过程中的剩余时间;ti,o为计划开始滑行时间;si为航空器i滑行路径的长度;为理想状态下的滑行时间;为航空器i为避免冲突产生的额外等待时间;Ei为航空器i的优先级,航空器根据Ei的大小确定通过冲突区域的先后顺序;Δti为航空器因避免冲突所造成的时间损失;P为燃油单价;Ki为航空器i的耗油率;H为旅客单位延误成本;Ni为航空器i的旅客数。
时间富余度Ti(fy)在运行过程中随进程更新,刻画航空器i完成滑行任务的紧迫程度。当Ti(fy)>0,即航空器预计提前到达滑行终点时,应将油耗成本作为优先级的参考因素;当Ti(fy)≤0,即航空器预计将发生滑行延误。
2 算法实现
2.1 算法设计
生物地理学算法(BBO)中的可行解对应自然界中的栖息地,栖息地的优劣程度以适宜程度(Habitat Suitability Index,HSI)衡量,并作为个体优劣排序的依据,HSI 越高表明栖息地越适宜。HSI的设置结合模型的目标函数式(1),并对冲突锁死情况进行惩罚,即

式中:fHSI为适应度函数;Xlock为冲突锁死的次数;C为对应的惩罚系数;M为用于调节数量级的正常数。
根据BBO算法的基本原理,设最大迁入、迁出概率分别为E和I,满足E=I=1,每个栖息地的迁入概率μz,迁出概率λz分别为
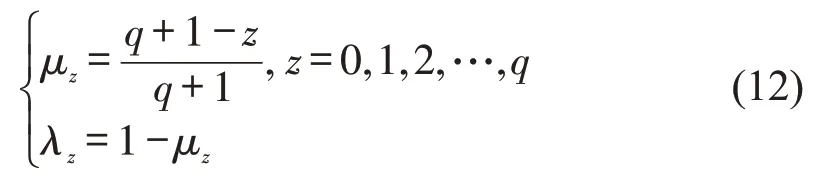
式中:q为栖息地最多可容纳的种群数量;z为栖息地当前所拥有的种群数量。z由HSI 唯一确定。设当前栖息地总数为h,序列中第g个栖息地的当前种群数为z=h-g。
采用轮盘赌的方式随机产生新的X′替换原物种X。设栖息地g发生变异的概率为wg,其中,wmax为最大突变概率,Ph-g为栖息地中当前物种数量对应的概率,Pmax为Ph-g的最大值,计算公式为
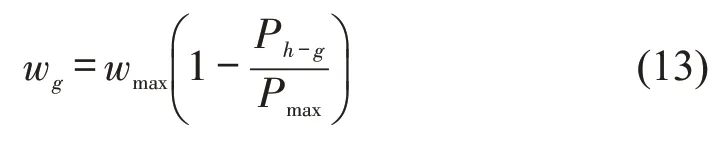
2.2 滑行道仿真设计
所有航空器均沿其规划路径滑行至终点。赋予各航空器经过节点的时间信息,记作Bts=(i,m,c,t′),其中:i为航空器编号;m为节点编号;c为该节点在航空器i的滑行路径中的序号;t′为航空器i无冲突到达节点m的时间。例如,Bts=(2 ,18,5,463)表示2 号航空器无冲突到达节点18的时间为463 s,其中,节点18在该航空器的路径中为第5 个节点。将所有节点按时间先后升序排列,生成含有节点信息的时间轴BTS=(Bts1,Bts2,…,Btsa)。从起始时间节点Bts1=(i1,m1,c1,t′1)起,搜索安全时间间隔δ内的所有航空器信息,判断m是否相同,如果相同,表明两架航空器发生冲突,需要进行冲突解脱。保持第一架通过该节点的航空器的信息不变,从第2架通过该节点的航空器开始,直到最后一架通过该节点的航空器,通过优先级依次判断后续航空器通过该节点次序,其实际到达该节点时间依次顺延。随即相应更新上述航空器通过后续节点的时间信息,重复搜索安全时间间隔这一步骤。示例如图2所示。
3 仿真验证
选取我国某大型机场某日18:00-19:00的42架航空器作为研究对象,对滑行道调度进行仿真,机场实际场面滑行道运行数据,如具体机型参数,各机型航空器滑行过程中标准载客量,耗油和滑行速度如表1所示(数据来源于所选取机场的管制塔台专业技术手册)。机场场面构型如图3所示,Q8 为进场航空器着陆点,Q9为起飞跑道端点,滑行道系统共有70个节点。

图2 航空器冲突解脱示例Fig.2 Example of aircraft conflict relief
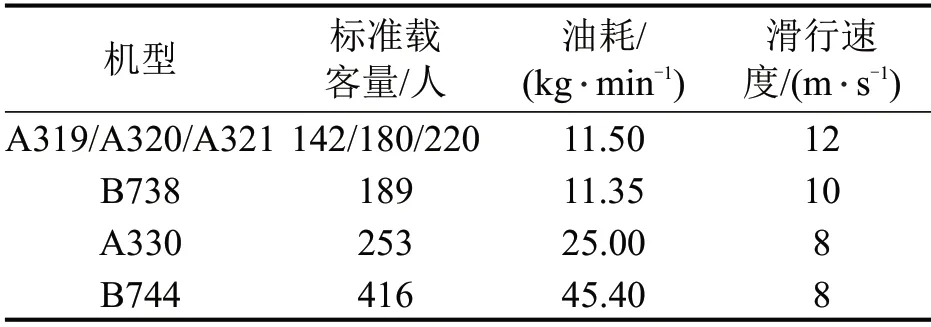
表1 各机型标准载客量、油耗和滑行速度Table 1 Standard passenger capacity,fuel consumption and taxi speed of each model
航油价格以国家发展改革委2018年12月份核定的航空煤油价格4547 元⋅t-1为标准。假定每位旅客等待成本为1.7元⋅min-1。
3.1 优化结果分析
通过不断仿真验证,栖息地规模设为100,突变概率为0.08。不同滑行策略下的滑行道调度进化曲线如图4和图5所示。
FCFS(First Come First Service)策略下航空器总滑行时间稳步下降,最优解出现在第196 代,此时航空器总滑行时间为12614 s;同时,航空器总到达误差整体呈下降趋势,过程中波动幅度较小,原因在于FCFS 仅考虑滑行时间最小化,无法调整延误时间较长航空器的优先级以提高准时性,滑行调度缺乏动态性。TMC 策略优先保证航空器准时性,以总到达误差为主要目标,最优解出现在第189代。与FCFS相比,TMC策略下总滑行时间从第17至第132 代上下波动剧烈,曲线锯齿状明显,总滑行时间由12614 s 提高至12930 s,增加了2.3%;但TMC 策略以小幅增加总滑行时间为代价,使航空器总到达误差缩短946 s,减少63.1%,提高航空器准时性,有利于提升旅客满意度。FCFS 策略与TMC 策略体现了滑行时间与准时性两者的博弈。两种策略下仿真结果如表2所示。各航空器到达 滑行终点时间误差对比及分布如表3和图6所示。
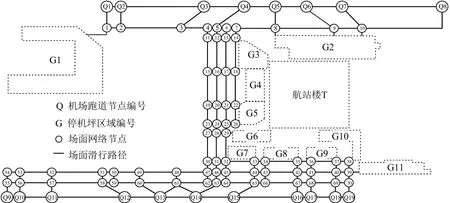
图3 国内某机场滑行道网络拓扑图Fig.3 Topology diagram of taxiway network in a domestic airport

图4 FCFS策略迭代结果Fig.4 FCFS strategy iterative result
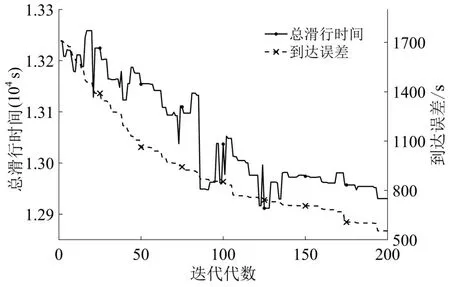
图5 TMC策略迭代结果Fig.5 Time margin control strategy iterative result

表2 FCFS与TMC仿真结果对比Table 2 Comparison of simulation results of FCFS and TMC
从图6和表3可以看出,FCFS策略下航空器到达误差超过30 s的有16架,占比38.1%,其中6架航空器到达误差在1 min以上。而TMC 策略下40 架航空器准时性指标完成度较高,比重高达95.2%。仅14 号、18 号两架小机型航空器到达误差超过30 s,分别为97.5 s 和34 s,分别为B738 和A322 机型。其中14号航空器滑行路径与其他航空器重合区域较多,导致冲突等待时间较长,因此准时性较差。相比于FCFS策略,TMC策略将所有冲突航空器总到达误差从1175.9 s 降至397.9 s,减少66.2%。可见TMC 策略可以将更多冲突解脱时间分配给时间富余度较大的航空器,从而提高延误航班的准时性。
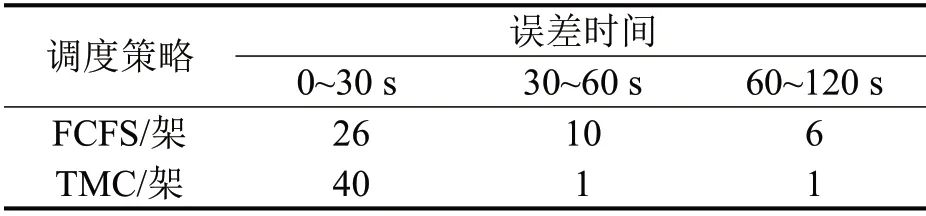
表3 不同到达误差时间段航空器数量对比Table 3 Comparison of number of aircraft in different time periods of arrival error
3.2 冲突解脱分析
表4为FCFS 策略与TMC 策略下航空器冲突次数与解脱时间对比,发生冲突航空器等待次数如图7所示。
FCFS 策略下航空器共发生18 次滑行冲突。18次冲突由12架航空器分配,除2号、4号和7号这3 架航空器分别承担2 次、3 次和3 次冲突以外,其余航空器均只发生1 次冲突。TMC 策略下共发生12次冲突,减少33%,除去1次交叉点冲突,其余11次均为超越冲突。在航空器滑行过程中,发生超越冲突的解脱方式为后机减速,与前机保持相同速度,直至2 架航空器共用路段节点分离后,后机恢复原速度继续滑行。

图6 各航空器到达误差分布Fig.6 Arrival error distribution map of each aircraft

表4 航空器滑行冲突次数与解脱总时间对比Table 4 Comparison of aircraft taxi conflicts and total free time
交叉点冲突解脱是根据优先级别的高低安排在冲突节点的滑行顺序,2 架航空器在满足安全间隔后方可通过冲突节点。其冲突解决过程大大增加了管制员的工作负荷。因此TMC策略将交叉点冲突转化为超越冲突,能够在航空器运行安全的前提下降低滑行道调度难度。FCFS 与TMC 两种策略下滑行距离增量如图8所示。

图7 航空器冲突等待次数对比Fig.7 Comparison chart of waiting times of conflict aircraft

图8 各航空器滑行距离增量对比Fig.8 Comparison chart of increment of taxiing distance of each aircraft
两种策略下,绝大多数航空器选择最短路滑行。FCFS策略下总滑行距离增量为3830 m,其中,8 架航空器滑行距离增量超过400 m,6 架为大型机,2架为小型机。TMC策略下总滑行距离增量为4440 m,比FCFS策略增加610 m。4架航空器滑行距离增量超过400 m,其中,13 号航空器为大机型航空器,其余3架均为小型机。11号和21号这2架航空器均为时间富余度较大的航空器,滑行距离均增加1060 m。为保障时间富余度较小航空器的准时性,其以牺牲自身滑行距离为代价,优先保障其他航空器的滑行。TMC策略将滑行距离较长的路线更多分配给小型机,符合实际运行中优先保障大型机的规则,有利于减少机场和航空公司双方运行成本。
4 结论
本文在兼顾航空器油耗与载客量的动态优先级基础上,设置以航空器滑行时间富余度为主,以最小化航空器到达误差和场面滑行时间为调度目标,建立基于TMC 的滑行道调度优化模型。结果表明:TMC 策略下航空器到达滑行终点的准时性提高显著,航空器到达误差显著降低,航空器场面运行效率得以有效提升。考虑航空器滑行准时性的场面调度研究目前比较少,未来的研究应考虑如何在机场协同决策环境下,在保证航空器滑行准时性基础上实现后续停机位的指派和跑道的调度,从而提升整个场面的联合调度效率。
