考虑出行者行为的多重网络拥堵风险传播模型

黄建华，孙梦歌

(福州大学，经济与管理学院，福州350116)

0 引言

交通拥堵预警信息可以通过影响出行者对拥堵状态的心理感知而影响出行者的出行路径选择，从而改变城市路网的交通流量分布。诸多研究表明，出行者的路径选择行为受自身潜在心理变量影响。韩春阳等[1]揭示了出行者个体对城市道路交通拥堵状况的感知差异，道路特征、交通流量及个人属性均对出行者的拥堵感知有显著影响；HOOI L.K.[2]发现，出行者出行选择与其所感知的拥堵程度密切关系，随着拥堵感知程度的增加，其更改出行路线的可能性也随之增长；尚华艳等[3]研究表明，通勤者对公交车内部拥挤的敏感度越高，越会尽量地避开高峰出行。此外，出行者面对拥堵风险的态度，还受性格、年龄、性别等诸多因素影响。田丽君等[4]发现，个体路径偏好对城市交通网络中均衡状态的流量分布具有影响；俞礼军等[5]应用Weibull随机交通分配模型，揭示随机路网中具有风险偏好倾向的驾驶员会导致路网总出行时间增加，以及加剧瓶颈路段的交通拥堵；HUA X.[6]将驾驶员分为明智、保守、敏感和跟随4 种类型，其中，越理性和不保守的驾驶员，越容易频繁地切换路径，导致网络交通流不稳定，驾驶员敏感度越高，交通流维持稳定可能性就越大。

从研究方法来看，考虑到城市交通网络拥堵的传播过程类似于病毒的传播过程，基于易感-感染-恢复(Susceptible-Infective-Recovered, SIR)的病毒传播模型被广泛应用于分析城市交通拥堵风险传播机制问题[7]。由于城市交通网络系统中存在信息传播网络、城市道路网络等多维度的子网络，且信息网络中拥堵预警信息会对交通网络中出行者的行为产生影响，以WANG Z.S.[8]为代表将SIR 模型引入到多重网络上，应用微观马尔科夫链方法(Microscopic Markov Chain Approach,MMCA)探讨其传播机制；周艳等[9]构建交通拥堵与预警信息交互传播模型，分析预警信息影响下的城市交通网络拥堵传播问题，且发现预警信息在网络中传播能在一定程度上缓解交通拥堵问题；HUO L.A.[10]进一步探讨预警信息下考虑羊群心理和风险偏好的双重网络风险传播问题。

综上所述，现有研究主要考虑出行者性格、偏好等心理因素对出行行为的影响，以及对双重乃至多重网络上的信息、风险和拥堵传播机制问题的探讨。本文以现有成果为基础，对以下方面进行探索：一是在分析国内典型城市路网特征的基础上，生成符合真实城市路网特征的网络模型，揭示其在拥堵传播方面与经典随机网络的差别；二是应用微观马尔科夫链方法替代蒙特卡罗模拟进行数值分析，以便更好地解决交通流量分配与路网节点状态转移问题；三是基于城市道路网络、预警信息传播网络及居民出行网络等构成的3 重耦合网络模型研究拥堵风险传播问题，并考虑预警信息下出行者行为特征对拥堵风险传播的影响。

1 问题描述与建模

1.1 模型假设

为便于分析，提出以下假设：

(1)出行子网。城市居民出行演化网络具有择优和生长的特性，网络拓扑结构类似无标度网络，本文假设出行网络和路网中的节点间进行多对一的符合无标度特征的连边操作，表示交通流分配具有无标度特性，当节点拥有相对较大的交通流时，更易发生拥堵。

(2)道路子网(拥堵传播层)。以道路交叉口或站点为节点，以实际道路为边，表示路网中拥堵风险的传播关系，其中，每个节点拥堵风险传递的3种状态为：易感(S)，感染(I)和恢复(R)。

(3)信息子网(信息传播层)。节点与道路子网相同，边代表节点之间是否能进行正常通信，受出行者社交网络影响，本文假设信息子网为小世界网络。在信息传播层，节点有2种状态，即处于U(Unaware)状态的节点没有任何信息，处于A(Aware)状态的节点有预警信息。

(4)一旦节点受到风险感染，就会立即获得风险传播的警告信息。对于节点，状态U将立即更改为状态A，其概率为1。

感染率Mij取决于易感节点i的“易感性”和感染节点j的“传播能力”。即

式中：Ai=1-hi，当节点i与拥堵节点接触时，拥堵增长率为1-hi，其中，hi=h0×Vi，Vi为分配到节点i的交通流，即出行子网连接到信息子网节点i的度值，h0为出行者拥堵敏感程度，出行者拥堵敏感程度越高，拥堵规避行为越明显，0 ≤h0≤10。本文将出行者对交通拥堵的感知评分分为4个等级，即(1 ,3] 为畅通，(3,5] 为轻度拥堵，(5,7] 为中度拥堵，(7,10 ]为重度拥堵。Tj=βj，受感染节点j的基本传播概率，大的负载流量节点会加剧邻居节点的感染概率。

建立3层交通拥堵传播网络模型，如图1所示。图1中，道路子网和信息子网之间的各种状态组合，共有5 种类型(US，AS，AI，AR，UR)，未知的感染状态(UI)除外。随着时间的发展，两层之间的耦合动态连续迭代。

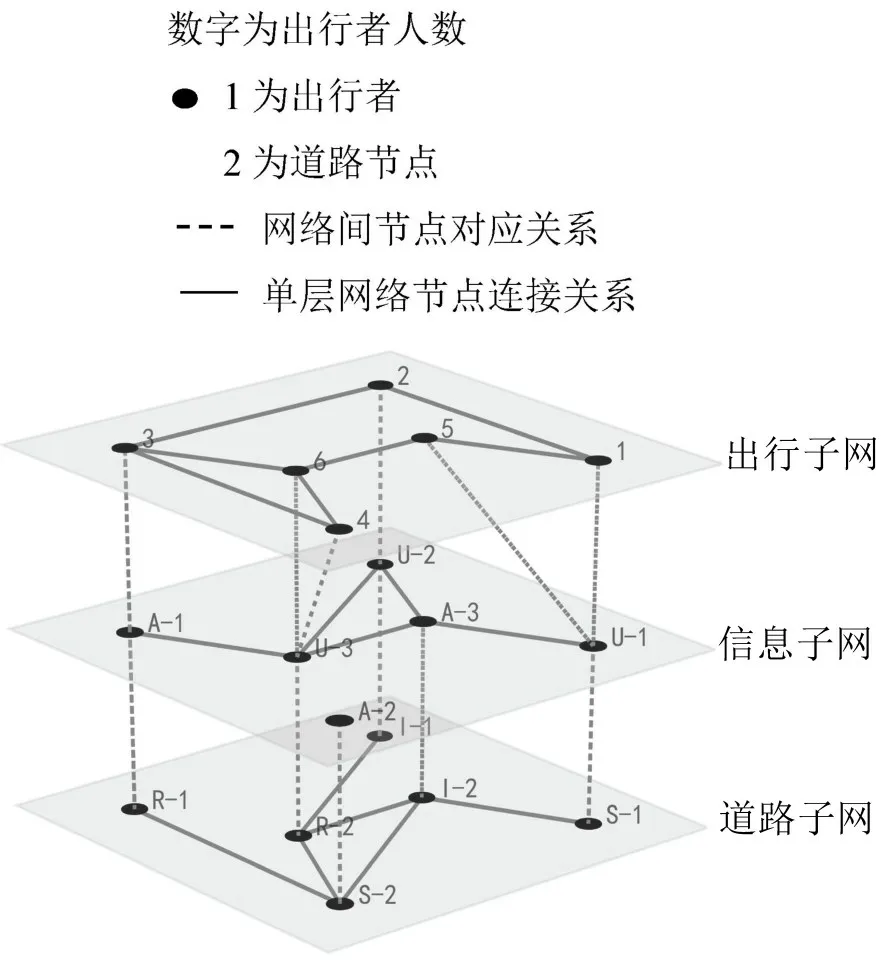
图1 UAU-SIR模型中使用的多重网络Fig.1 Schematic diagram of multiply networks used in UAU-SIR model

1.2 预警信息

为描述节点预警信息程度，用η(0 ≤η≤1) 表示，当η=0 时，表示节点得不到任何预警信息，不影响风险传播；当η=0.5 时，表示节点已经获得一定的预警信息，可以采取一定的防护措施，抑制风险传播。考虑路网拓扑结构和出行网络交通流分配对节点拥堵风险传播率和恢复率的影响。

没有预警信息的节点i被感染的概率βi(U)为

有警告信息的节点i被感染的概率βi(A)为

被感染节点i的恢复率μi为

式中：为路网中节点i的路网结构特征值，取介数中心性(Betweenness Centrality)表示；为出行子网分配到路网的交通流，取度中心性(Degree Centrality)表示；β0为初始传播率；μ0为初始恢复率。

2 模型和MMCA分析

将拥堵预警信息下的网络交通流演化过程抽象为马尔科夫过程，根据离散时间马尔可夫链方法在复杂网络流行病分析中的变体MMCA，建立UAU-SIR 模型5 种可能状态的动力学方程。首先，通过概率树方法揭示状态转移关系，如图2所示。

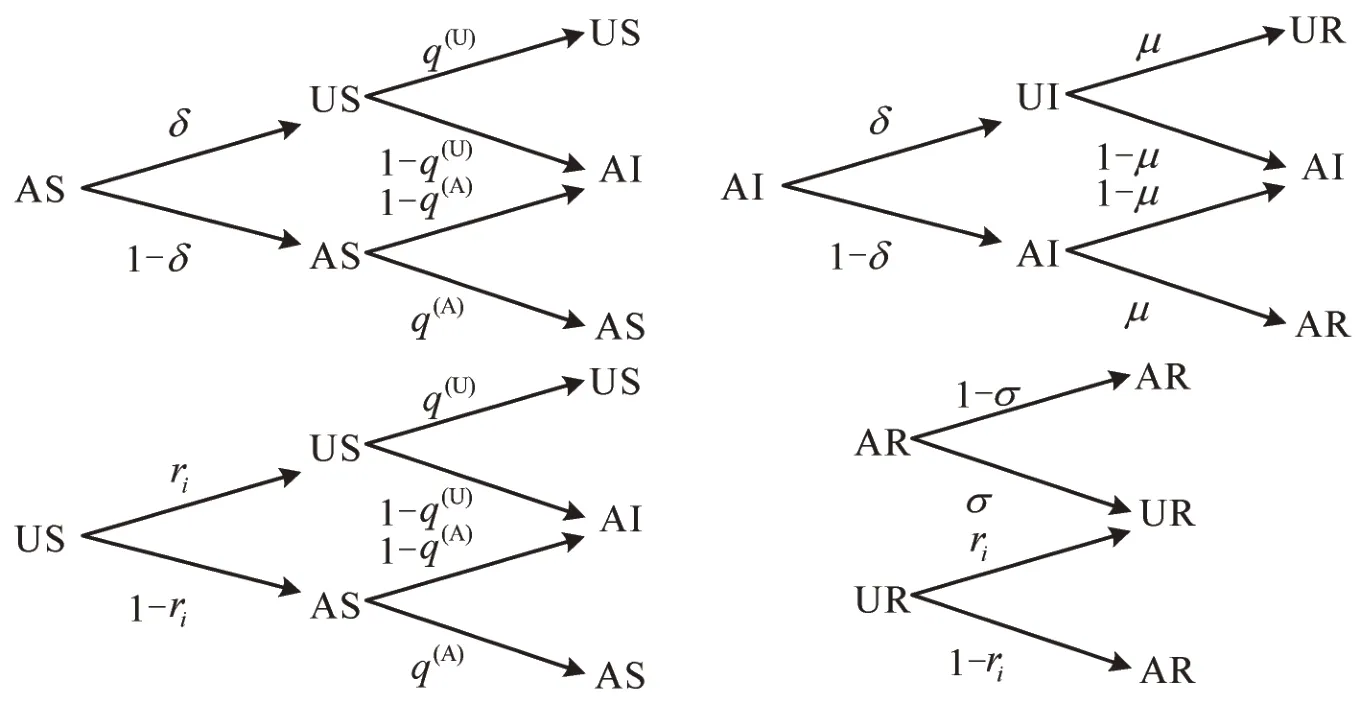
图2 UAU-SIR模型概率转移树Fig.2 Probability transition tree of UAU-SIR model

UAU-SIR模型是5种可能状态的概率传输树，包括：AS、AI、AR、US 和UR 状态。拥堵风险传播模型参数及描述如表1所示。

每个时间步骤中，状态转换过程在信息和拥堵风险传播之间交替进行。每一个时刻t，节点只能处于5 种状态中的一种，对应比例分别为Pi(US)(t)、pi(AS)(t)、Pi(AI)(t)、Pi(UR)(t)和Pi(AR)(t)。

2.1 风险偏好

考虑出行者路线选择中风险偏好行为对拥堵风险传播的影响，在UAU-SIR模型基础上，考虑出行网络分配到路网的交通流和出行者个体风险偏好属性对拥堵风险传播影响。将拥有不同交通流的道路节点风险属性定义为αi=α0×Vi，其中，α0为出行者风险偏好大小，1 ≤α0≤10。本文以下列两种类型出行者对交通拥堵风险传播造成的影响为例进行分析。

表1 3层拥堵风险传播模型参数及描述Table 1 Parameters and corresponding description of existing three-layer congestion risk propagation model

(1)风险偏好型出行者

(2)风险规避型出行者

因此，得到

2.2 MMCA分析

根据图2中状态转移，用MMCA方法建立5个可能状态的动态演化方程为

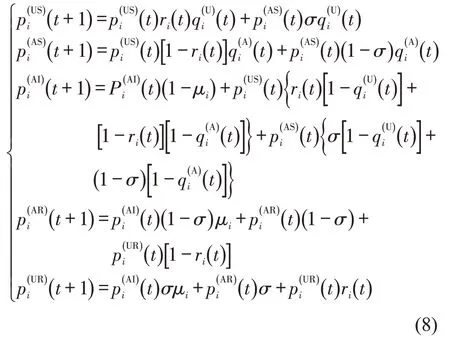
式中：t为当前时间步骤；t+1 为下一个时间步骤。 在每一个时间步骤中都有，以满足正常情况。当时间步长足够大时，各节点状态的比例达到稳定状态。当t+1趋向无穷大时，有

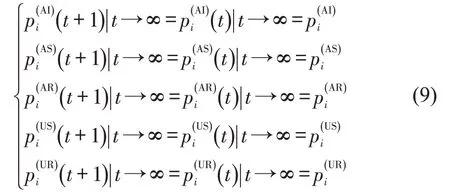
传染阈值是重要参数，决定风险是否最终爆发或死亡。传染性临界阈值的估计是分析现有模型特点的第一步。在临界点附近，任何被感染节点的概率都接近0，故可以假设pi(AI)=εi≪1。因此，基于上述的假设和公式，被周围任何感染节点感染的概率为

εj上的高阶项忽略不计，因为它在流行阈值附近足够小，设

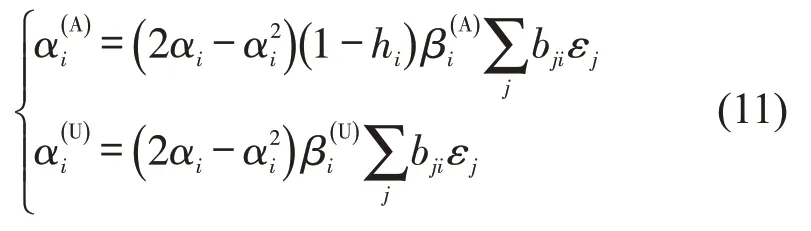
将αi(A)和αi(U)代入式(8)前3个方程，则

当t→∞，忽略高阶项转化为

进一步转化为

进一步转化为

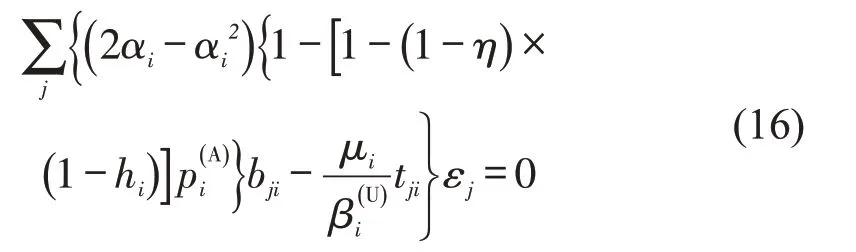
式中：tji为单位矩阵元素；令hji=(2αi-α2i){1-，Λmax为矩阵最大特征值，在这个模型中，传染病的流行阈值可描述为

临界阈值βi(C)可以看作是特征值问题的一个解，与信息层的动力学特征有关，尤其与信息层参数Pi(A)和出行者拥堵敏感程度hi有关。初始传播率，风险偏好对其有一定影响。从传染动力学角度看，流行阈值代表感染率临界值。超过这个临界值，拥堵风险就会沿着道路网络广泛地分散到各路口。

3 数值模拟与结果分析

分析国内典型城市道路网络数据发现，道路网络的度分布近似泊松分布。国内典型城市道路网络统计特征如表2所示。

表2 国内典型城市道路网络统计指标Table 2 Statistical indicators of road network in typical cities in China

泊松分布的K-S 检验P 值均大于0.050，可知，路网结构整体类似ER 随机图网络，局部具有小世界特性或无标度特性。没有度大的节点，度值分布均匀，节点度值大多集中在1～4，度值为3的节点占比最多，平均度在2.6790左右。并且拥有较短的平均路径和较小的集聚系数。因此，本文根据实际道路网络节点度值分布规律生成模拟路网用于仿真，同时与ER 随机网络仿真结果对比，研究网络拓扑结构的影响。

为进一步研究UAU-SIR模型中路网络拓扑结构出行者风险偏好和拥堵敏感程度对交通拥堵传播机制的影响，给出不同参数下恢复节点比例。所有MMCA均值超过100次运行，选择6个交通流量最大的节点设为感染节点，信息遗忘率设置为0.3，感染节点初始恢复率设置为0.5。同时，利用微观马尔可夫链方法(MMCA)，对式(8)的每个时间步进行迭代，得到相应的结果，如图3～图6所示。

图3 预警信息、拥堵敏感度、初始传播速率对恢复节点比例的影响Fig.3 Influence of warning information,congestion sensitivity and initial propagation rate on proportion of recovery nodes

图4 预警信息、风险偏好、初始传播速率对恢复节点比例的影响Fig.4 Influence of warning information,risk preference and initial propagation rate on proportion of recovery nodes

图3给出系统达到稳态时模拟路网和ER随机网络中恢复节点比例ρ(R)随初始传播率β0的演化趋势。恢复节点比例随初始传播率β0和拥堵敏感度h0的增加而增加；预警信息(η=0.5)时恢复节点比例ρ(R)增长较缓慢且小于无预警信息(η=0)时，表明预警信息对风险传播有抑制作用；当感染率小于阈值βi(C)时，交通网络中没有拥堵风险；相比于模拟路网，ER 随机网络不同预警信息和拥堵敏感度恢复比例相差不明显，拥堵风险爆发阈值更低，传播范围更广，网络拓扑更加脆弱。

图4表明：恢复节点比例随初始传播速率β0增加而增加，随风险偏好a0增加而下降；预警信息时，恢复节点比例增长较缓慢且小于无预警信息(η=0)时；随着α0增长，出行者更倾向于追求风险，风险更容易在交通系统中传播；当感染概率小于阈值βi(C)时，交通网络中没有拥堵风险；相比于模拟路网，ER 随机网络不同预警信息恢复比例相差不明显。

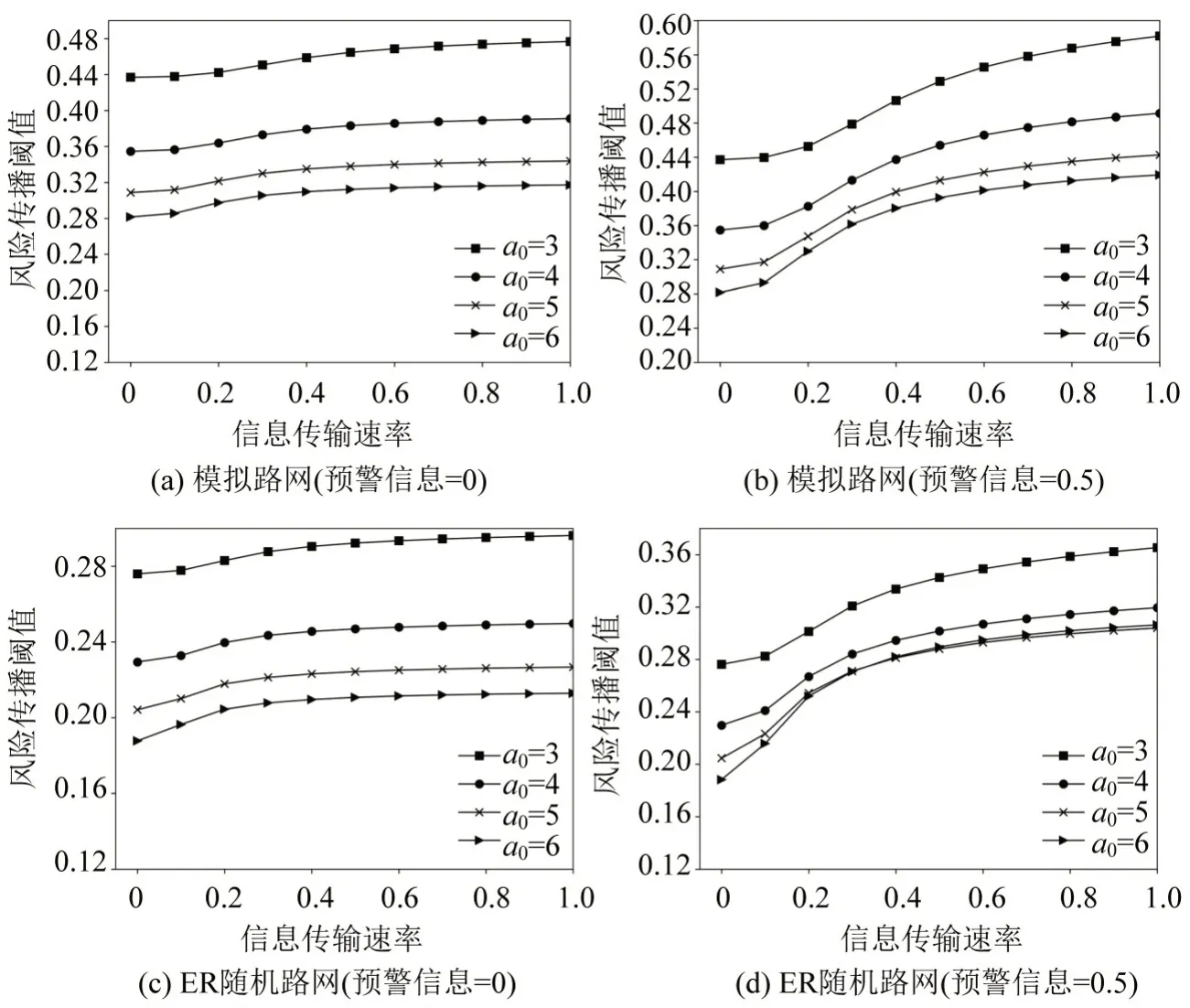
图5 预警信息、风险偏好、信息传输速率对拥堵风险传播阈值的影响Fig.5 Influence of warning information,risk preference and information transmission rate on congestion risk propagation threshold

图6 预警信息、拥堵敏感度、信息传输速率对拥堵风险传播阈值的影响Fig.6 Influence of warning information,congestion sensitivity and information transmission rate on congestion risk propagation threshold

图5表明：拥堵风险传播阈值βi(C)随信息传输速率λ增加而增加，随风险偏好α0增长而降低；可以看到α0=5 和α0=6 曲线相差不大，说明当风险偏好大于一定值时，α0增长对拥堵风险传播阈值影响不大；预警信息(η=0.5)时，风险传播阈值更高，随信息传输速率波动更明显；ER 随机网络的风险爆发阈值相比模拟路网更低。说明路网拓扑设计、预警信息传输速率对抑制拥堵风险传播至关重要。

图6表明：拥堵风险传播阈值βi(C)随信息传输速率λ和拥堵敏感程度h0增加而增加；预警信息(η=0.5)时，风险传播阈值更高，随信息传输速率波动更明显；ER 随机网络的风险爆发阈值相对更低；说明提升出行者对拥堵状态的感知有利于治理交通拥堵。

4 结论

城市道路拥堵传播过程受预警信息和出行者路线选择行为影响，本文提出多重网络UAU-SIR模型，综合考虑预警信息传播、交通流分配、出行者行为特征，以及路网拓扑结构的影响，利用微观马尔可夫链方法(MMCA)，构造描述预警信息传播和拥堵传播之间可能的状态转移概率树，并推导节点拥堵传播的临界阈值。通过数值模拟分析得到：预警信息在交通严重拥堵时能在一定程度上降低传播规模；预警信息下出行者拥堵敏感程度越大，拥堵风险传播阈值越大；出行者风险偏好越大，拥堵风险传播阈值越小；相比模拟路网，ER 随机网络传播速度更快、风险阈值更低、传播范围更广。本文结果表明，交通信息服务提供者在设计道路导航系统时，应考虑出行者的不同风险态度和拥堵敏感程度；提升预警信息传输速率有利于治理交通拥堵。多重网络中考虑出行者行为特征的交通拥堵和预警信息交互传播，为研究城市交通拥堵提供新的视角。