考虑弹性需求的城市枢纽间多方式时刻表优化

卢天伟，姚恩建*,b，杨扬,b，郇宁，陈琳

(北京交通大学，a.交通运输学院；b.综合交通运输大数据应用技术交通运输行业重点实验室，北京100044)

0 引言

随着城市群交通基础设施建设和联乘出行服务的大力发展，枢纽间乘客出行需求日益增加，出行方式日趋多样化。在此过程中，准确把握枢纽间综合运输通道各方式的乘客出行需求，调整匹配枢纽间时刻表与客流需求之间的关系，是提升乘客联乘服务体验，优化枢纽供需关系的关键。然而，目前枢纽间多方式运力协同性欠缺，导致当前运力配置不合理；或因时刻表调整优化导致枢纽间乘客出行需求弹性变动，使供需关系难以达到最终的均衡状态。因此，有必要考虑弹性需求对城市枢纽间多方式时刻表开展针对性地优化研究。

时刻表优化研究主要分为单方式和多方式两类。在单方式时刻表优化方面：Li 等[1]考虑公交续航里程和充电约束，构建了混编公交时刻表优化模型；朱宇婷等[2]根据轨道交通网络周期性运行特点，考虑拥挤及换乘客流脉冲性到达特征建立了轨道交通时刻表优化模型；张桐等[3]以减小列车总出行时间和总能耗为目标，提出考虑节能目标的有轨电车时刻表优化方法；Lu等[4]分析不确定条件下机场巴士弹性需求，提出了机场巴士时刻表优化方法；许得杰等[5]考虑轨道交通客流时变特性，构建了时变需求下的轨道交通时刻表优化模型。多方式时刻表协同优化方面：龙海波等[6]运用熵权法对多方式协同节点延误风险进行了评价，构建了考虑转运延误风险的分区段多方式协同货运运力优化模型，但其研究对象为货运，无法直接应用于客运时刻表优化；赵璐阳等[7]以广义运输成本最小为目标，对运输通道内多方式列车开行方案进行优化，但其前提假设为各方式需求固定不变，没有考虑其中的需求变动，可能导致最终供需不匹配问题。

综上，已有研究主要针对单方式，或假设需求固定的多方式时刻表优化，对于联程出行运输通道多方式为场景的相关研究较少，缺少考虑弹性需求的枢纽间多方式时刻表优化研究。基于此，本文对枢纽间乘客出行方式选择行为进行建模，分析时刻表优化方案实施导致的各方式出行需求变动，并提出枢纽间多方式时刻表协同优化模型及算法，为枢纽间综合运输通道运力优化提供方法支持。

1 乘客出行方式选择模型

为量化研究枢纽间各方式时刻表变动对出行需求的影响，基于多项Logit(Multinominal Logit,MNL)模型对枢纽间乘客出行方式选择行为进行建模。MNL 模型假设乘客在相互独立的方式集合中，选择对个人效用最大的出行方式，能够较好地描述乘客出行方式选择行为[8]。图1为本文构建的乘客出行方式选择行为模型结构，备选方式包括轨道交通、地面公交、机场巴士、出租车4 种方式，影响因素包括出行时间、出行费用、步行距离。

根据上述模型结构，模型数学表达式为

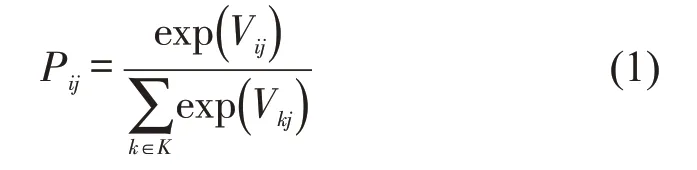
式中：Pij为乘客j选择方式i的概率；Vij、Vkj为乘客j选择方式i、k的效用函数；K为备选方式集合，i∈K，k∈K；θk为方式k的固有哑元；Xkj1、Xkj2、Xkj3分别为乘客j乘坐方式i的出行时间、出行费用和步行距离变量；βk1、βk2、βk3为待估参数。

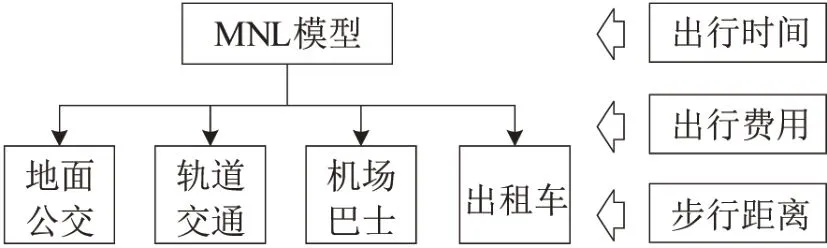
图1 乘客出行方式选择行为模型结构Fig.1 Structure of passenger mode choice behavior model

为标定模型参数，本研究于2020年3月1日-3月15日开展了枢纽间乘客出行方式选择行为调研，回收有效样本数据1524份，作为模型参数估计的输入数据，参数估计结果如表1所示。为评判模型有效性，本文对模型的ρ2、t值进行计算。其中，各变量t值绝对值均大于1.96，说明各变量对方式选择影响显著；ρ2大于0.2，说明模型精度较高[9]，能够较为合理地刻画乘客出行方式选择行为，为后续建模中量化时刻表优化导致的弹性需求提供方法支持。

表1 模型参数估计结果Table 1 Parameter estimation result of model

2 枢纽间多方式时刻表优化模型

2.1 问题描述

针对图2所示过程进行建模，其中，枢纽间包含多种出行方式，各方式路径中可能包含单段或多段线路，每条线路包含多个车次，模型主要通过对枢纽起点站及枢纽间沿途换乘站各车次时刻表的调整，考虑其中乘客方式选择变化，提升各方式线路之间的协同性，实现乘客等待总时间的缩短。

时刻表调整会在一定程度上影响线网中其他站点的服务水平，故本文采用多目标优化模型，同时考虑乘客换乘等待时间、时刻调整数量、时刻调整总时间的最小化，最终可得多个不同调整程度的时刻表优化方案，供运营单位根据优化结果和对其他站点影响程度择优选择。

图2 枢纽间多方式时刻表优化示意图Fig.2 Schematic diagram of multi-modal timetable optimization between transport hubs

针对上述枢纽间多方式时刻表优化问题，在建模前进行如下前提假设：

(1)各方式的出行路径固定，部分方式的路径中存在换乘，乘客到达换乘站后会换乘该方式下一线路的车次；

(2)乘客的方式选择结果根据MNL 模型得出的各方式选择概率随机确定。

2.2 模型构建

令i表示枢纽间任一出行方式中某线路的某一车次，I表示所有方式线路的所有车次集合，i∈I；j表示枢纽间具有乘车需求的任一乘客，J表示乘客集合，j∈J；k表示枢纽间任一出行方式，K表示所有出行方式集合，k∈K；t表示优化时刻范围内的任一时刻，T表示优化时间范围，t∈T。模型涉及的其他参数变量如表2所示。

模型的目标函数及约束条件如下。

(1)目标函数

(2)约束条件

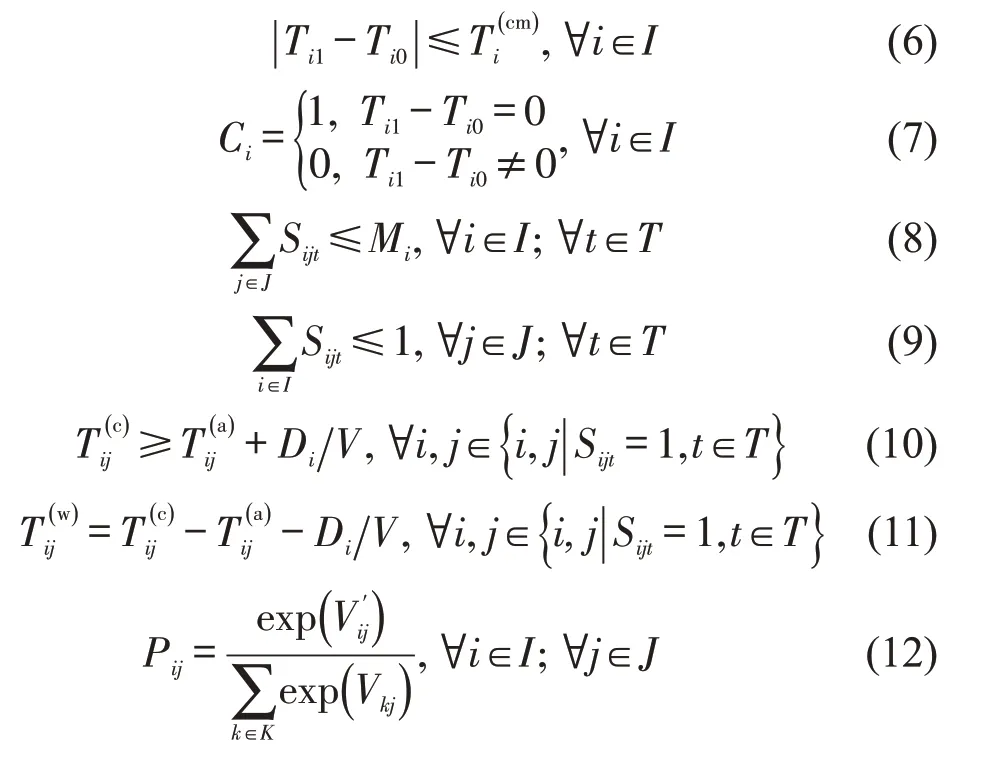
表2 模型参数及变量Table 2 Model parameters and variables

式(3)～式(5)分别表示乘客等待总时间、时刻调整数量、时刻调整总时间的最小化，其中，乘客等待总时间包括乘客枢纽起始站等待时间及出行过程中的换乘等待时间。式(6)为时刻调整幅度约束，Ti(cm)可综合考虑优化幅度和对线路中其他站点的影响程度对其约束值进行设置。式(7)为车次i是否进行时刻表调整的判别约束。式(8)为车次容量约束，表示乘车人数不大于最大可用容量，其值可根据车次容量、满载率、站点非枢纽客流需求占比进行计算。式(9)为乘车状态判别约束，表示乘客j在时刻t的乘车状态约束；当Sijt=1 时，表示乘客j在时刻t为在车状态、无法乘坐其他车次；当Sijt=0时，表示乘客此时为非在车状态、可考虑乘坐或换乘车次。式(10)和式(11)为时间窗约束，表示乘客在始发站或换乘站的乘车时刻不小于到站时刻与站内步行时间之和，乘客等车时间为乘车时间与到站时间、站内步行时间之差；其中，Tij(a)、Tij(c)可在求解过程中根据调整后的时刻表，结合容量限制约束进行确定。式(12)为乘客方式选择约束，表示乘客j选择车次i对应出行方式的概率，时刻表的调整优化会使乘客出行时间发生变化，导致方式选择时不同出行方式的效用发生改变，其中，Vi'j、Vkj可采用式(2)根据时刻表调整后的出行时间进行计算。式(13)为乘客等待时间约束，表示乘客j选择车次i的最大等待时间。式(14)为最小发车间隔约束，表示相邻车次最小间隔。式(15)为0-1变量约束。

3 求解算法

枢纽间出行方式具有较高的发车频率和灵活的调整方案，模型的可行解规模庞大，且模型中对弹性需求的考虑使之变为非线性问题，需采用启发式算法进行求解，故本文采用快速非支配排序遗传算法(Nondominated Sorting Genetic Algorithm Ⅱ，NSGA-Ⅱ)[10]求解。在模型求解过程中，首先需要对时刻表优化方案实施后的客流加载过程进行仿真，以计算得到优化目标，故将NSGA-II 算法与客流加载仿真过程相结合，具体流程如图3所示。

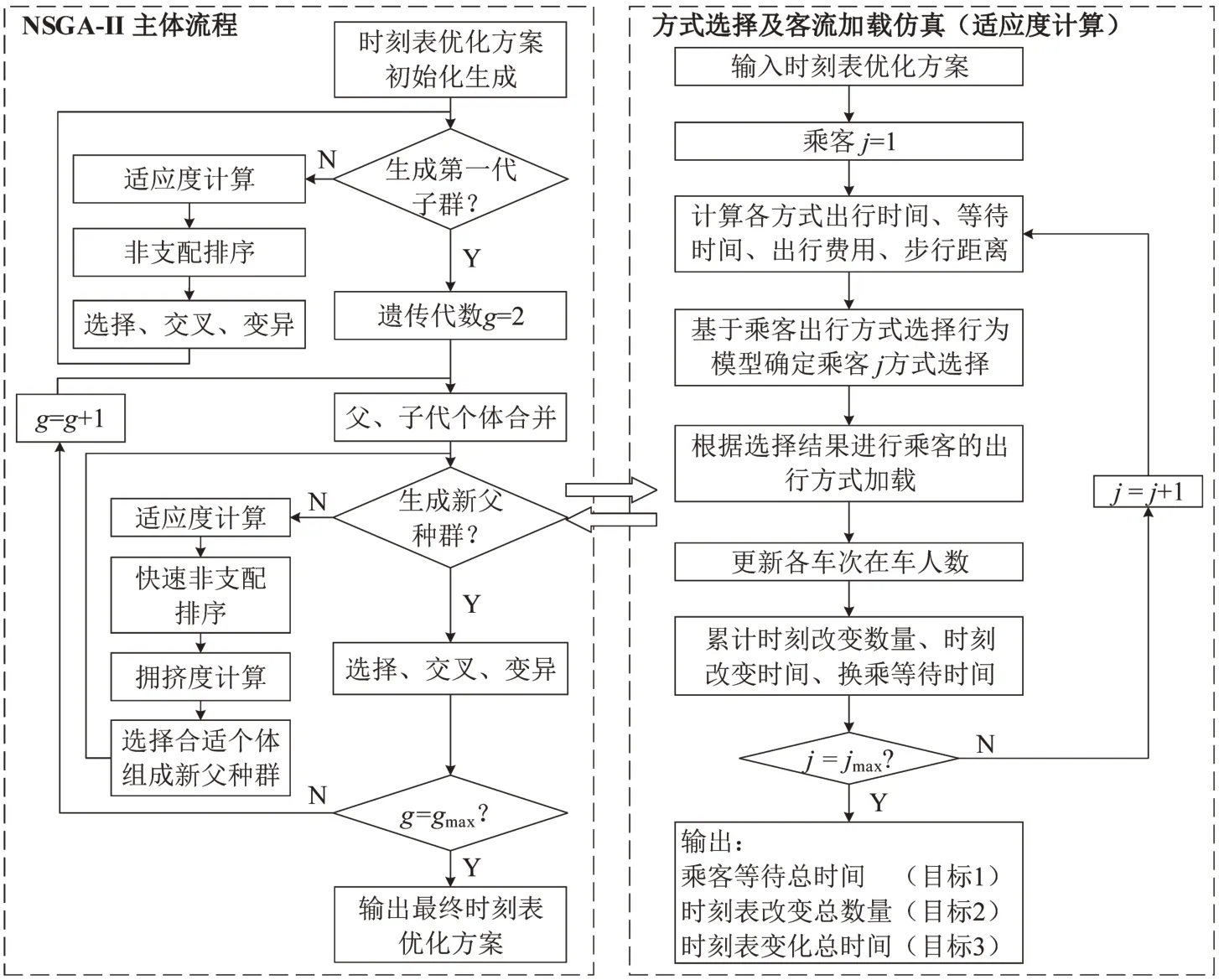
图3 枢纽间多方式时刻表协同调度优化求解算法流程Fig.3 Optimization algorithm for multi-mode timetable collaborative scheduling between transport hubs

各方式时刻表优化方案通过染色体编码生成。采用整数编码反映时刻表排序，每个被编码染色体代表各方式时刻表的一种随机调整方案，如图4所示。图中各基因代表某种方式对应的发车时间，整个染色体的基因序列代表调整后的时刻表。

图4 染色体(时刻表优化方案)编码示意图Fig.4 Chromosome(timetable optimization scheme)coding

最终求解得到一组帕累托最优解，为评判各解的优劣性，采取单位改变时刻表数量和单位改变时间两者的乘客等待时间缩短百分比加权值λ作为指标，与方案的合理性呈正相关关系，计算方法为

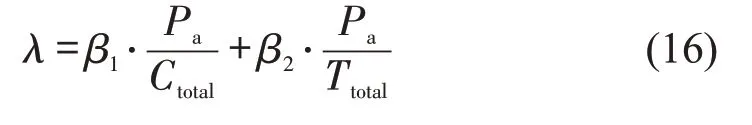
式中：λ为评价指标；Pa为乘客等待时间缩短百分比；β1、β2为加权系数。

4 案例分析

以北京南站-北京首都国际机场为案例场景，检验本文提出模型及算法的有效性。该场景包含轨道交通、地面公交、机场巴士、出租车4 种方式，如图5所示。由于枢纽间乘客对时效性要求较高，且同一出行方式不同路径的出行费用基本相同，乘客主要集中选择出行时间最小的路径，故各方式选取的路径均为枢纽间客流较为集中的路径。本案例针对前3 种方式的时刻表进行调整，以2019年5月8日9:00-13:00枢纽间客流数据作为输入进行多方式时刻表优化。

为验证模型有效性，除考虑弹性需求的改进模型外，同时采用假设需求固定的传统模型进行对比分析。改进模型和传统模型均采用相同参数的NSGA-II算法，种群规模为100，迭代次数为500，交叉概率为0.8，变异概率为0.2。在运行效率方面，经多次算法过程的执行，两模型的算法平均执行时间分别为1138 s 和1069 s，表明执行时间属于可接受范围，可用于求解更大规模的时刻表优化问题。

为验证算法有效性，进行多次算法执行试验。设置如下有效性判别条件：(1)算法最终相邻变化的目标值之差需小于0.1%；(2)接下来的100次迭代的最优目标值不再发生改变。若同时满足上述两个条件，则将本次求解看作为有效求解流程。

算法迭代过程中的乘客等待时间寻优过程如图6所示。可以看出，传统模型最终在第149 次得到最优解，乘客等待时间为7.53×106s；改进模型因考虑弹性需求，在迭代过程中包含因出行方式改变而缩短的乘客等待时间，最终在第346次迭代得到最小的乘客等待时间，即7.23×106s，较传统模型缩短了3×105s，且满足有效性判别条件。

改进模型迭代过程的各方式需求变动如图7所示。可以看出，随着迭代次数增加，乘客对各方式的选择比例也不断变化，说明时刻表优化方案的实施使各方式产生了较为明显的需求弹性变化效果。其中，地面公交、出租车选择比率相对稳定；轨道交通的乘客等待时间较短，机场巴士较长，因此迭代过程趋于机场巴士选择比例逐渐降低，轨道交通比例逐渐升高，最终分别降低和升高了10.73%、10.05%。

图5 北京南站-北京首都国际机场出行方式及线路Fig.5 Travel modes and routes of Beijing South Railway Station-Beijing Capital International Airport

图6 乘客等待时间迭代寻优过程Fig.6 Iterative optimization process of passenger wait time

最终求得帕累托关系如图8所示，目标函数值及乘客等待时间缩短百分比如表3所示。可以看出，相对于传统模型，改进模型可得到更多的时刻表优化方案，且能够以较少的时刻表变化在更大幅度上缩短乘客等待时间。

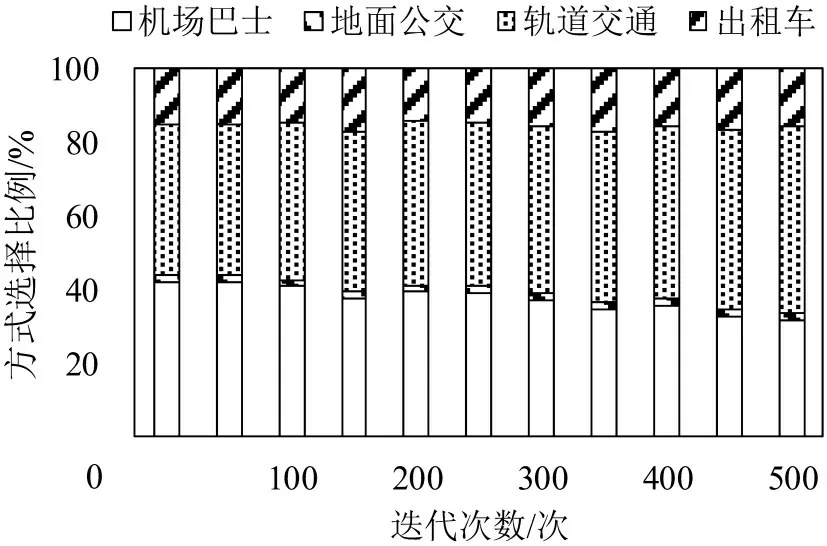
图7 改进模型的方式选择比率迭代变化过程Fig.7 Iterative process of mode choice ratio of proposed model

采用式(12)评价指标，对上述帕累托解的优劣性进行定量评估，得到各方案评价指标λ如表4所示。

由表4可以看出，改进模型得到的时刻表优化方案的评价指标整体优于传统模型。其中，改进模型方案7的评价指标最大，说明其能够以相对最小的时刻表改变缩短最多的乘客等待时间，为最优方案。因此，选定方案7 为最终时刻表优化方案，其乘客等待总时间为7.58×106s，较原方案缩短了10.36%。具体优化方案如图9所示，包含各车次时刻调整方案，运营管理单位可兼顾对其他站点服务水平的影响来调整或加开各车次。

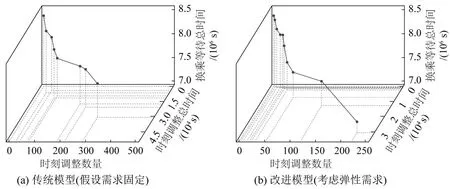
图8 两种模型求解得到的帕累托图Fig.8 Pareto relations solved by two models

表3 帕累托最优解对应目标优化结果Table 3 Objective optimization results corresponding to Pareto optimal solution

表4 帕累托最优解的评价指标λ 计算结果Table 4 Evaluation index calculation results of Pareto optimal solutions

图9 最终时刻表优化方案Fig.9 Final timetable optimization scheme

5 结论

本文提出考虑弹性需求的城市客运枢纽间多方式时刻表优化方法，并以北京南站-北京首都国际机场为案例进行有效性检验。结果表明，时刻表优化方案的实施对各出行方式产生了较为明显的需求弹性变化效果，其中，机场巴士的需求比例降低10.73%，轨道交通的需求比例上升10.05%。对模型求解得到10 种时刻表优化方案，其评价结果整体优于传统模型。最终筛选时刻表优化方案实施后的乘客等待总时间为7.58×106s，较原方案缩短10.36%，提高了城市枢纽间多方式时刻表的协同性和合理性，为城市群多模式客运枢纽一体化运行关键技术研究提供支持。