基于出行不均匀分布的通达型公交网络

郭晨，王建军，霍月英，邱志宣

(1.长安大学，运输工程学院，西安710064；2.内蒙古大学，交通学院，呼和浩特010070；3.重庆交通大学，交通运输学院，重庆400074)

0 引言

发展高质量的公共交通是缓解交通拥挤的重要措施之一。高质量的公交应该包括以下元素：①城市内良好通达且便于乘客记忆的线路，通达性良好的公交线路有利于吸引更多出行多变的乘客，便于乘客记忆的线路有利于吸引不会使用智能设备或对公交线路不熟悉的群体；②在可接受步行距离内的公交站点；③高频率、长时段的公交运行时刻表，可以提升乘客候车和换乘时间的灵活性，乘客无需随公交时刻表变更出行时间[1]。出行需求的空间分布对高质量公交的线路设置、公交频率和公交站距的设计产生较大影响。大量研究关注均匀分布出行需求下公交网络设计问题。但许多城市出行需求的空间分布是不均匀的，不均匀分布的出行需求更容易引起交通拥挤。因此，对于不均匀分布出行需求下的公交网络进行研究更加迫切且重要。

公交网络可分为“直达型网络”“通达型网络”两类[1]。目前大部分研究集中于直达型网络，该网络主要基于乘客的OD 矩阵进行规划。虽然该类型网络的直达乘客比例高、换乘次数小，但具有线路非直线系数和公交线路重复系数高，公交公司成本高，客流量较低起讫点间乘客出行不便等缺点。当城市扩张时，公交线路需要重新规划，才能满足因城市变化出现的新需求。通达型网络是基于城市形态规划的。虽然其直达目的地的乘客比例低，但具有公交线路非直线系数和公交线路重复系数低，公交公司成本低，全部公交线路的频率高，城市间任何一对起讫点间出行便捷，乘客“门到门”的平均出行时间较短等优点。当城市扩张时，公交线路易拓展，线路无需重新规划。基于此，本文对出行需求不均匀分布的通达型公交网络进行研究。

已有大量学者对“通达型网络”进行研究。Daganzo[2]提出基于需求均匀分布的正方形城市的网格放射混合网络，该公交网络的成本小于私家车，具有较强的竞争力。该网络可以在几乎不增加公交公司成本的情况下，大幅降低乘客的出行时间。Estrada 等[3]将Daganzo[2]研究结果应用于巴塞罗那，把巴塞罗那的城市结构抽象为矩形，长宽比是2∶1。Badia等[4]提出面向放射环型城市结构的通达型公交网络。Badia等调查了欧美城市的公交分担率和换乘率，发现即使乘客换乘次数会增加，但线路简洁、站点覆盖率高、高频率、通达性良好的公交网络仍具有较强的吸引力。对比公交网络改造前后的巴塞罗那发现，随着不同公交网络改造阶段逐步完成，公交分担率持续上升[5]。Nocera 等[6]基于上述研究，提出城市居民少于100万城市的通达型公交网络模型。综上发现，现有研究集中于出行需求空间分布均匀的通达性网络设计。而市中心靠近城市边界的城市形态，如中国汕头，大连，呼和浩特，美国的旧金山等，其出行需求分布严重不均匀，对其构建通达型公交网络可有效缓解交通拥挤、提升交通效率，但研究这类城市通达型公交网络的较少。

为探究城市市中心靠近城市边界且需求不均匀分布的高质量公交系统特点，本文建立公交线网规划、站点和频率设置的综合模型，同时分析模型中各个参数的弹性系数和敏感性。在此基础上，探讨目标函数、决策变量和约束条件随空间需求的变化，讨论空间需求变化与公交系统稳定性的关系。

1 公交网络

本文提出的公交网络面向市中心靠近城市边界且需求不均匀分布的城市。这里假设市中心和整个城市均为正方形，如图1所示，图中，D为城市边长，d为市中心边长，，不同线形表示不同公交线路。

图1 网格放射混合公交网络示意图Fig.1 Radial and grid hybrid model

公交网络在市中心为网格状，在水平和垂直两个方向都有公交线路；在郊区是放射状，仅在水平或垂直方向有公交线路，为保证空间覆盖率，郊区增设支线，如图1所示。郊区线路离市中心越远，车头时距越长。

使用需求函数，不使用OD 矩阵，有利于城市发展和刺激新的需求。假设市中心出行均匀分布，郊区出行随着与市中心边界距离增加而线性递减，市中心出行量是城市边界出行量的f倍。为便于建模，引入参数k，设市中心出行需求密度函数为1，则郊区出行需求密度函数为()1-kx，x为出行位置距市中心边界距离，

2 模型建立

本文目标函数由公交公司成本和乘客成本组成。公交公司成本包括修建公交线路成本，高峰小时车辆行驶运行成本和高峰小时运行车辆购置成本[2]。乘客成本包括到达公交站点和从站点到目的地时间期望，候车时间期望，车内行驶时间期望和换乘时间期望[3]。由于目标函数各个部分单位不同，将公交公司各部分成本转换为平均每位乘客出行时间并分别乘以对应权重，即乘客成本的4部分分别乘以权重wA，wW，wT，we。

乘客基于全有全无分配法分配。乘客选择公交线路假设如下：

(1)乘客按照最少花费选择线路；

(2)乘客选择离自己最近的公交站，当有两个公交站距离一样时，乘客随机选择；

(3)乘客在第一个可换乘的站点换乘。

模型各个参数含义如表1所示。

表1 各参数含义Table 1 Meaning of each parameter

构建模型为

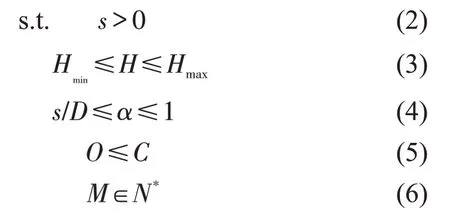
式(1)为目标函数，第1 个中括号为公交公司成本，第2 个中括号为乘客成本；式(2)约束公交站距大于0；为防止串车且保证时间覆盖率，式(3)限制车头时距下限和上限[4]；式(4)保障城市中心区与整个城市的比例在合理范围；式(5)保证车内高峰小时关键线的最大客流量不超过公交车容量。决策变量为α、H、s。模型中各个参数推导过程见附录A。

3 模型分析

3.1 算例分析

基于数据可得性和已有研究成果，参数取值如表2所示。BRT 相对于常规公交和地铁是最佳公交模式[2]，故选择BRT作为研究模式。本文城市规模和出行需求与巴塞罗那一致[3]。时间价值参考文献[8]，其他参数参考文献[2-7]。

采用Lingo软件求解，51 s获得全局最优解(当f=2.5 时，36 min 获得全局最优解)。模型结果如表3所示。市中心面积约占城市面积的0.43，车头时间为4 min，公交站距约为600 m，公交运行速度约21 km·h-1。每位乘客的总成本为1.78 h，平均乘客感知时间为1.18 h，平均乘客出行时间为0.74 h，公交机构成本对于每个乘客而言为0.59 h。

表2 各参数取值表Table 2 Value of model parameters

表3 模型结果Table 3 Model results

3.2 灵敏度分析

3.2.1 决策变量灵敏度分析

研究每个决策变量变化对总成本、公交公司成本和乘客成本的影响。分析某个决策变量时，其余决策变量为常数且为最优解。图2(a)～(c)分别显示α、H、s变化时各成本变化曲线。

图2 各决策变量与成本和占有率函数关系图Fig.2 Cost and occupancy curve for every decision variable

当α变化范围在-23%～46%，系统总成本增加10%以下，乘客成本在14%～-6%，而公交公司的成本在-23%～50%。H变化范围在-50%～25%时(2 min ≤H≤5 min)，系统总成本增加不超过6%，乘客成本变化在-8%～4%，公交公司的成本变化在43%～-8%。s变化在-16%～66%(500～1000 m)时，系统总成本增加不超过9%，乘客成本变化在-7%～3%，公交公司的成本变化在2%～-42%。公交公司成本和乘客成本变化方向相反，限制了总成本的变化范围。模型稳定性好，用于实际设计时，可根据需求调整参数。

3.2.2 输入参数灵敏度分析

模型结果受输入参数影响。表4评估了最佳方案的弹性系数。总成本对于模型的任何输入参数都表现为非弹性。参数的变化对模型结果影响较小。弹性系数变化较大的是μ对乘客成本和公交机构成本，但两者弹性变化趋势相反，故抵消了对总成本的影响。vw对乘客成本及总成本影响较大，因此乘客可选择速度更快的方式，如共享单车、社区微循环公交等，可以显著降低出行成本和时间。

3.2.3 空间需求灵敏度分析

图3为目标函数和决策变量随出行需求分布的不均匀性变化趋势。当f增加时，ZU下降明显，Z和ZA缓慢下降。出行需求越集中于市中心，公交公司成本越显著下降，乘客平均出行时间缩短。但市中心与郊区需求差异不宜过大，当f ＞1.6 时，站点间距和市中心占城市比例会突变，公交系统需要重新调整，会影响公交系统稳定性。

表4 输入参数的弹性Table 4 Cost elasticities of the best solution

图3 空间客流量变化与成本和决策变量函数图Fig.3 Cost and decision variables curve for space demand changing

4 结论

本文构建了市中心靠近城市边界且需求不均匀分布的城市公交线网规划、站点和频率设置的综合模型，同时分析模型中参数的弹性系数和敏感性，探讨了空间需求变化的影响。主要结论如下：

(1)该类型城市通达型网络公交频率约为4 min，市中心约为城市面积的64%，公交站距约为600 m，公交运行速度在21 km·h-1左右。

(2)模型对输入参数和决策变量稳定性好。决策变量变化范围在-50%～46%，系统总成本增加不超过10%。模型可行性强，用于实际设计，可根据需求调整决策变量。总成本对于任何输入参数都表现为非弹性，参数变化对模型结果影响较小。乘客进入和离开公交系统的速度对乘客成本及总成本影响较大，因此乘客选择速度更快的方式，如共享单车或者公交微循环线路可显著降低出行时间。

(3)需求越集中于市中心，越有利于降低总成本，但公交网络布局稳定性下降，会削弱公交竞争力。当需求过度集中于市中心时，即f ＞1.6，公交系统需要重新调整，以满足突变的需求，但经常变化的公交网络会削弱公交的稳定性和竞争力。

附录A

L的推导：参考文献[2]。

V的推导：。市中心双向车辆行驶距离是市中心线路长度的2倍，市中心每小时行驶的总距离。郊区车头时距不是恒定的，郊区每小时车辆行驶的总距离VP为车流量和每辆车辆行驶距离积分

M的推导：参考文献[3]。

vc的推导：车辆行程时间(1/vc)包括：(i)车辆行驶时间，(ii)停靠站点总时间，(iii)乘客上下车时间

eT的推导：eT=P1+2×P2=1-P0+P2。乘客的起讫点位于城市任意位置，最多需要两次换乘即可完成出行。eT为零换乘概率P0、一次换乘概率P1和两次换乘概率P2函数。0 次换乘的概率为起讫点在同一线路的服务区域内，一条公交线路的服务区域是距站点的以内的区域，

只有起讫点在相同的郊区需要两次换乘，即

1次换乘概率等于总概率减去0次换乘和2次换乘概率，即P1=1-P0-P2。

A的推导：参考文献[5]。

W的推导：候车时间包括3 部分：(i)起点候车时间，WO；(ii)最后一次换乘，WD；(iii)第一次换乘候车时间，只有需要二次换乘的乘客需要第一次换乘。WO=WD，WO可以被划分为两种情况，起点在市中心和在郊区。在市中心，平均候车时间是乘以起点在市中心概率，在郊区，候车时间和距离市中心边界的位置有关。两个郊区区域是对称的，假设乘客出行起点距离市中心边界的距离为x，平均候车时间H(x)满足，因此，郊区平均候车时间为H(x)与起点在距市中心边界距离为x的概率积分，

T的推导：，E为车内行驶距离期望，车内行驶距离期望包括市中心EC和郊区EP两个部分。对于郊区，乘客沿放射网络出行。出行可能是进入或离开市中心。基于对称性，进入与离开市中心距离期望一样，东郊区和北郊区一致，以东郊区为分析对象。假设起点到市中心西侧距离为x，出行距离水平期望为，垂直期望为(x-d)。对不同位置距离期望和对应乘客的比例积分在市中心内，假设起讫点随机分布，乘客平均出行距离为水平方向的平均距离与垂直方向的平均距离之和，即，市中心出行距离期望为市中心乘客平均出行距离和概率的乘积

O的推导：

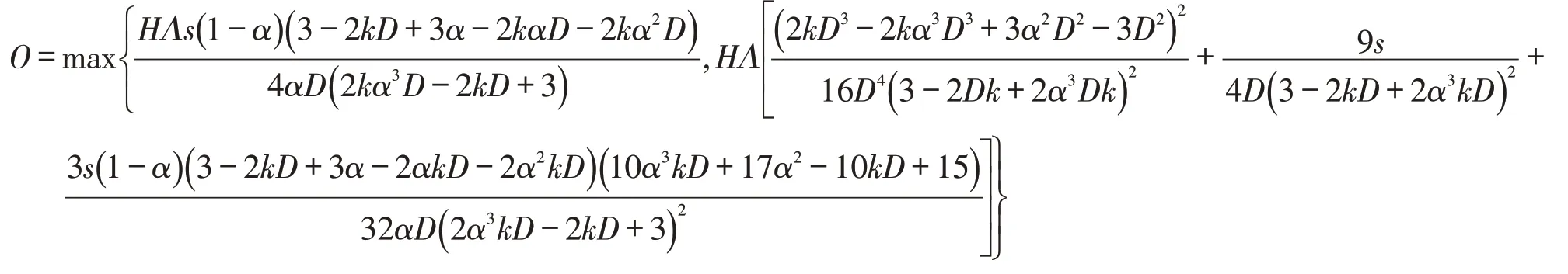
车内高峰小时关键线路的最大客流量是郊区车内关键线路最大客流量或市中心车内关键线路最大客流量的最大值。郊区关键线路最大客流量为接近市中心边界换乘的客流量，客流量关键线路车内最大客流量是平均值的2 倍[3]。市中心高峰小时关键线路的最大客流量在城市的水平或垂直方向对称轴上的线路，基于对称性，东西走向线路和南北走向线路相当，以东西走向线路为例，客流可分为：(i)起点在东郊区的北边，终点在其的南边的乘客；根据模型假设，乘客会集中选择市中心边界的线路换乘，高峰小时乘客数量为；(ii)平均每条线路市中心内部出行，高峰小时乘客数量为；(iii)平均每条线路高峰小时离开市中心的客流数量的2 倍。三类乘客数之和乘以H，即为市中心关键线路最大客流量。所以O中第1项是郊区关键线路最大客流量，第2项是市中心关键线路最大客流量的最大值。