基于电子支付数据的公交车厢满载率实时估算方法
2021-02-27韦清波苏跃江高媛杨敬锋莫竣杰
韦清波,苏跃江,高媛,杨敬锋,莫竣杰
(1. 广州市公共交通数据管理中心,广州510620;2.华南理工大学,土木与交通学院,广州510641;3.广州市交通运输研究所,广州510627;4.中山大学,广州510275)
0 引言
公交车厢满载率是指实际载客量与车厢额定载客量的比值[1],反映车辆内拥挤水平,是直接关系市民出行服务的指标之一。准确掌握车厢满载率是做好公交运营管理的重要前提,特别是“新冠肺炎”疫情期间,及时发现满载率过高的班次和站段等,可为公交企业优化调度提供有力数据支撑,降低车厢人群聚集风险。
随着公交信息化发展,公交满载率研究也逐渐增多,主要有3种方法:一是人工抽样调查方法,在成本、时效性、连续性等方面均存在不足;二是基于视频图像分析[2]或者射频、红外等检测设备的方法,但需较大软硬件投入;三是基于公交大数据挖掘分析,针对公交“一票制”下车不刷卡情况下乘客的多天连续跟踪监测[3],离线推断下车站点、断面客流量等。如胡继华[4-5]等提出拟合投币乘客出行轨迹,并推断公交断面客流;马超群[6]等结合土地利用和人口密度利用IC 卡信息推断客流量,但是较多模型的时效性难以满足实时监测、实时公交调度需求。
为此,本文从兼顾效率和准确性等角度,提出基于数据驱动的公交乘客实时OD估计方法,进而结合车辆调度数据、车辆属性数据实现车厢满载率的实时计算。
1 总体技术路线
随着国内公交信息化的快速发展,车辆位置、发班调度等数据基本实现实时自动采集,形成规模体系。且随着新型支付兴起,公交客流自动采集的范围和时效均大幅提升,如广州实现了电子支付(卡、码)数据的实时回传,占比超90%。为研究数据驱动、实时车厢满载率估算模型提供了可行条件。
1.1 数据基础
数据主要来源于公交及地铁电子支付数据、车辆运营数据、线路属性及其他数据等,如表1所示。

表1 基础数据内容Table 1 Basic data
1.2 技术路线
本质上,公交车厢满载率由“车载乘客量”决定。首先在上车刷卡(码)时即推断出所有“已上车乘客”的上下站信息(时间、站点等),并匹配车辆发班、报站信息得到当前公交车在已驶过站点的上下车人数,进而计算当前车载乘客量,最后根据核载转化为车厢满载率。主要步骤(图1)有:上车站点匹配、下车站点推断和车厢满载率计算等。
2 满载率实时估算模型
2.1 上车站点匹配
图2为上车站点匹配模型,主要依托公交车载终端实时回传的电子支付、公交报站数据,对支付时间和报站时间进行比对,以距支付时刻最近的报站记录(15 min内)所对应公交站点为上车站点。
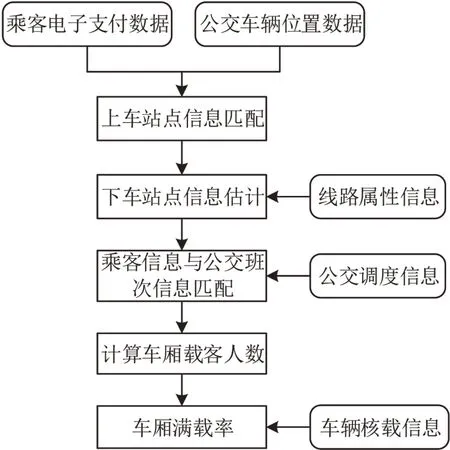
图1 技术路线Fig.1 Algorithm process

图2 上车站点匹配模型Fig.2 Model of boarding station matching
2.2 下车站点实时估计
实时运算需兼顾效率和准确度,本文构建乘客出行历史库,采用“K 近邻+出行小区估计+先验概率分配”组合模型推断下车站点,如图3所示,分别对应模型第1至第3层,不同层级之间按照“可推则尽推”原则耦合。
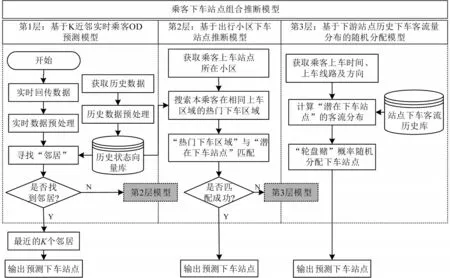
图3 下车站点组合预测模型Fig.3 Portfolio model of drop-off station estimation
2.2.1 基于K近邻的实时乘客OD预测
定义公交乘客出行状态向量为“每一位乘客历史出行过的公交线路、上车站点、时间及对应下车站点、出行频率”。对每一次完整出行记录进行归类,形成“历史状态向量库”。在下车站点实时预测时,根据当前出行线路、上车站点、时间等对“历史状态向量库”快速搜索,搜索出最相似的K个历史向量(“邻居”),再根据“邻居”推断下车站点。
(1)状态向量
状态向量由输入、输出向量组成,如图4所示。其中,输出向量即被预测目标——下车站点,输入向量则为影响“下车站点”的各种要素组合。根据各要素对目标的影响程度,选取身份标识(卡/码ID)、线路、乘向(上、下行)、上车站点及区域、时间作为输入向量,输出向量为下车站点及区域、出行频次。

式中:P为状态向量;c为卡/码ID号;l为线路号;d为乘向;us为上车站点;ua为上车区域;w为工作日,根据广州交通在非工作日、周一、周五、其他工作日的不同出行模式,分别用1、3、5 表示周一、二~四、五,用10表示非工作日以使得“非工作日与工作日的差异”大于“不同工作日之间差异”;t为刷卡所在小时;ds为下车站点;da为下车区域;v为出行频率。
理论上“历史状态向量库”时间跨度越大,存储数据越多,找到“邻居”概率增大,预测精度就越高,但运算效率也相应降低。状态向量库的大小建议由刷卡量规模、出行频率及运算硬件性能等综合确定。
(2)距离计算
距离用于判定“历史状态向量”与“被预测向量”的相似度,距离越小越可能成为邻居。由于状态向量中部分要素无法数值化,如卡号、线路号、上车站点等,对于该类要素需全字匹配后方可作为邻居;而对于可数值化的工作日、时间、乘向、频率等要素的距离计算,选取最常用的欧氏距离法,具体公式为

式中:Pf为被预测状态向量,Pf=(wf,tf,df,vf);Pi为历史状态向量,Pi=(wi,ti,di,vi);wf、tf、df、vf分别为预测向量的工作日、上车时间、乘向和频率;wi、ti、di、vi分别为历史向量i的工作日、上车时间、乘向和频率。
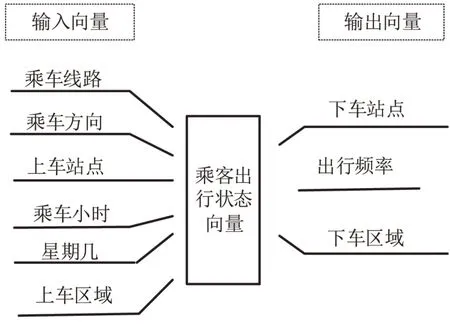
图4 状态向量Fig.4 State vector
(3)下车站点推断
根据式(1)计算“被预测向量”与各邻居的距离,从小到大排序筛选出距离最小的K个邻居,则以K个邻居里总频率最高的下车站点作为估算结果。
(4)状态向量库生成
“历史状态向量库”是K 近邻模型的运算基础,其中各向量的下车站点准确性将直接决定预测结果精度。由于历史库可离线生成,针对“一票制”乘车,可采取“基于乘客出行时空分布的下车站点离线推断方法”构建状态向量。其基本原理是:在公共交通出行链闭合(乘客出行均为公交或地铁出行)假设前提下,利用后次上车站点信息离线推断公交乘客本次出行的下车站点。第一,定义乘客“本次可能下车站点集D”,即所乘坐线路所有下游站点集合;第二,定义乘客的“后次上车站点集合O”,即后次上车站点及其周边(0.5~1.0 km半径内)站点集合;第三,若O⋂D=Q≠∅,则以Q中距离后次上车站点最近的站为本次下车站点,如图5中“站x”。
经测试,离线下车站点的推断准确率达60%~80%,准确性较高,可为“历史状态向量库”提供充足、准确的出行记录。
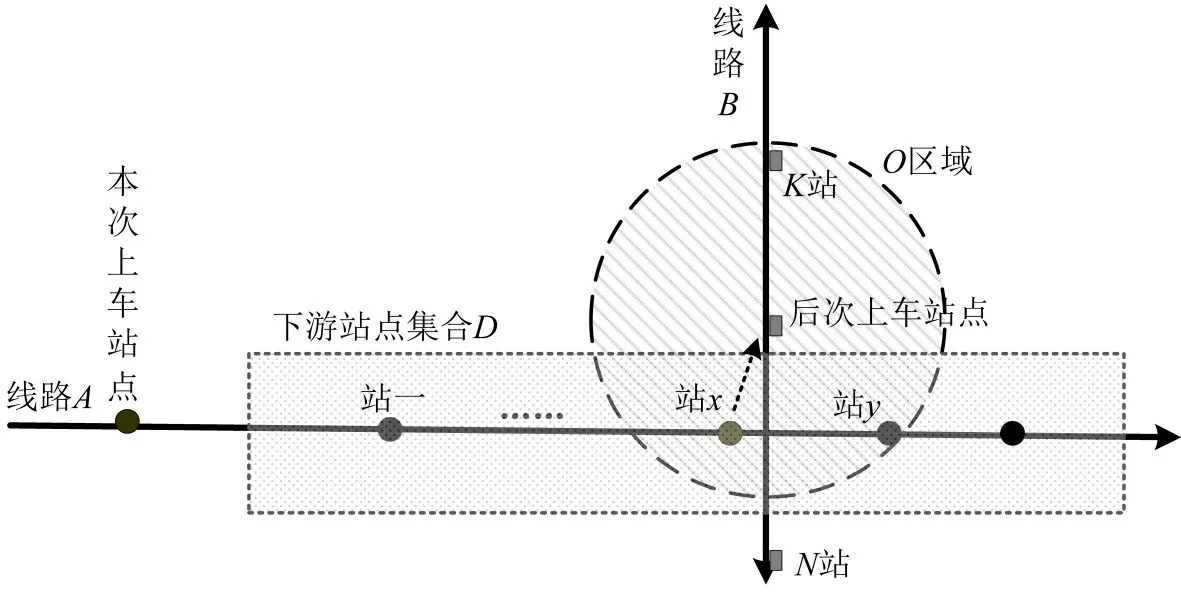
图5 离线推断乘客下车站点Fig.5 Estimating drop-off station based on next trip
2.2.2 基于出行小区的下车站点推断
根据式(2),K 近邻模型的邻居必须在“线路号”“上车站点”等要素上与“被预测向量”完全一致,但实际结果显示(见3.1 节)乘客选择固定“线路+站点”出行并不普遍,如果绝对采用“线路站点”来评判,可能导致较多潜在“邻居”无法使用,降低可推断率。如下列几种潜在“邻居”:线路相同上车站点不同但与当前上车区域一致,线路不同但上车站点一致,线路不同但上车区域一致,如图6所示。
为有效提升推断率和数据利用率,需在更大空间粒度(如“小区级”)下推断下车站点。提出“基于公交小区的下车站点推断方法”,即根据乘客历史出行热门区域推断下车站点。
首先,按照土地利用、经济社会特性、行政区划、干道分割等原则将公交线网划分交通小区,广州市域可分为184个公交小区,并利用地图匹配技术得到各公交站点所在区域。
其次,获取K近邻模型中未推断到下车站点的记录,假定任意一个记录的卡号为ci、乘车线路li、上车站点usi、上车小区uai,从“历史状态向量库”中找出卡号等于ci且上车小区等于uai的所有状态向量,进而得到热门下车交通小区集合A={da1,da2,…,daj} 及各小区出行频率。
再次,根据线路属性获取线路li在站点usi的下游站点集合D={si+1,si+2,…,si+j} 及下游交通小区集合S={ai+1,ai+2,…,ai+j} 。当A⋂S=G≠∅时,以G中频率最高的那个小区为乘客ci本次下车小区dai。
最后,以下游站点D={si+1,si+2,…,si+j} 中交通小区等于dai的第一站点作为本次出行的下车站点。
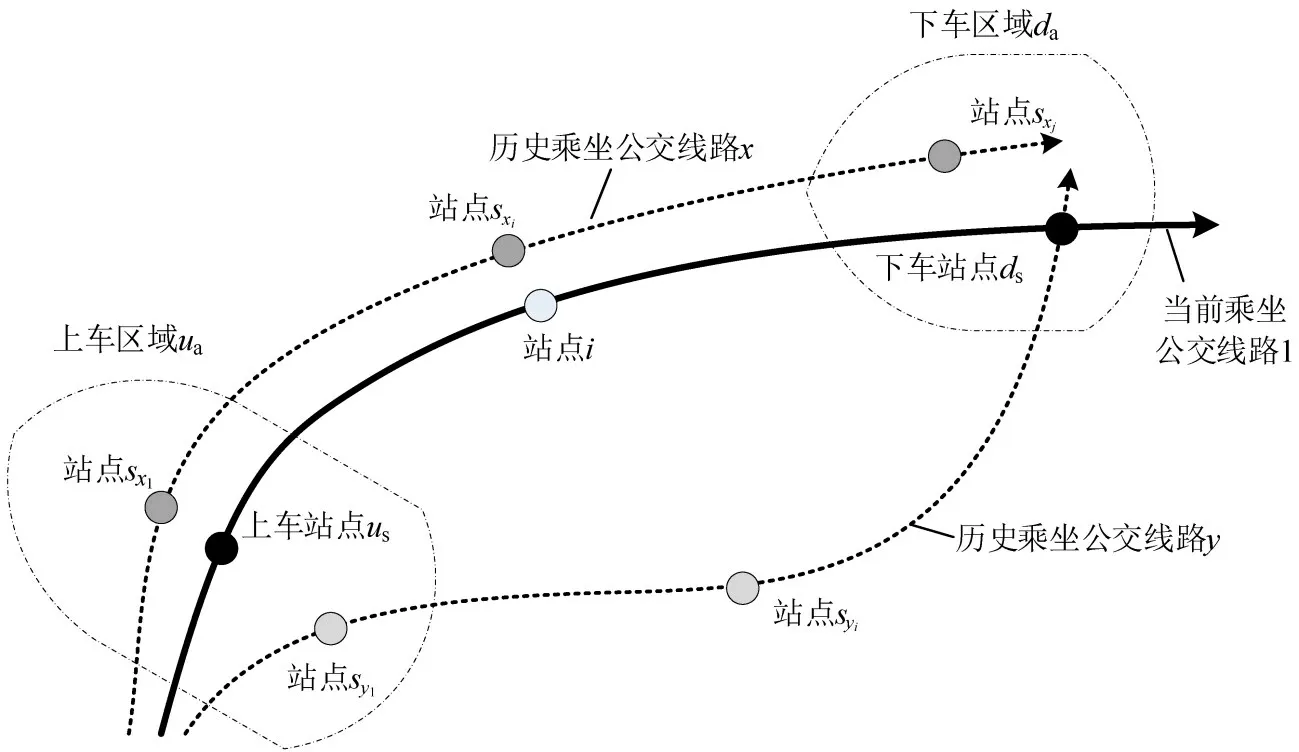
图6 基于小区的下车站点推断Fig.6 Estimating drop-off station based on traffic district
2.2.3 基于下游站点历史下车客流量分布的随机分配
当以上两种方法均无法推断下车站点时,说明该乘客属于偶发出行型,为保证结果完整性,可根据下游站点的历史“交通吸引度”,即下车客流量占比进行随机分配。主要是基于“下车站点客流流量越大,到达概率越高”的假设,按照先验概率推断乘客下车站点。
首先,以“小时”为单位,统计各线路、站点在全天不同时间点的下车客流量,得到“站点下车客流量历史库”。
其次,获取未推断出下车站点的记录,假定其任意一个记录卡号为ci、线路li、上车站点usi,从“站点下车客流量历史库”获取当前时点t、当前线路li在usi下游站点下车客流量信息N={Ni+1,Ni+2,…,Ni+j} 和下游站点集合D={si+1,si+2,…,si+j} 。计算各站点下车客流量占比为
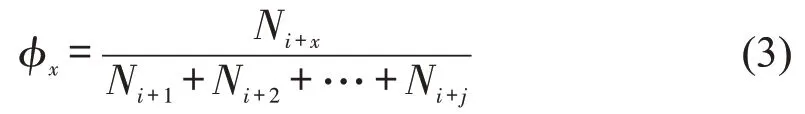
式中:ϕx为线路li在站点usi下游站点x的下车客流量占比。
最后,按照“客流量占比越大出行概率越高”的原则,利用“轮盘赌”算法随机推断本次出行的下车站点。
2.3 车厢实时满载率计算
总体上,上述组合模型可在乘客上车刷卡(码)时推断出其上、下车站点。在此基础上,结合车辆运营数据得到公交车在已驶过各站点的上、下车客流量,进而根据车辆核载计算车厢实时满载率。计算公式为
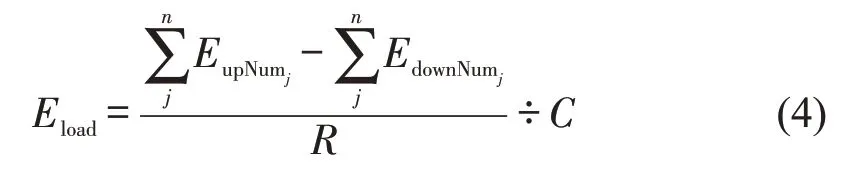
式中:Eload为当前车厢满载率;n为本趟公交车从首发站出发已驶过的站点数;EupNumj为本趟公交车在站点j的上车客流量;EdownNumj为本趟公交车在站点j的下车客流量;R为扩样比例,由电子支付比例等确定;C为车辆核载。
3 算例
根据上述算法,本文开发了“广州公交运行分析系统”,自2020年3月起实现满载率等指标的实时监测。以广州2020年5月-7月各一周数据构建“历史状态向量库”,得到657.3 万张卡/码的5166.8万个状态向量,并用8月18日429.2 万人次出行记录实时计算验证。运算过程中,为进一步保障实时效率,采用分布式存储和分布式计算不同车辆不同卡的出行链信息,按照尾号分类将“历史状态向量库”细分为10个子库,每个子库仅含约65万张卡的记录。
3.1 数据基本情况
分析一周(2020年7月20日-26日)数据基本情况,如图7所示,广州一周刷卡(码,下同)量约为2813.2万次,刷卡张数528.2万张,周平均刷卡次数5.3 次·(卡·周)-1。从周出行次数分布情况看,超过1/2(52.0%)卡的周出行次数在3 次以内,仅占出行量17.0%,属于偶发出行;而周出行次数超过8次的卡为114.2 万张,仅占21.6%,却贡献55.5%的出行量,以通勤出行居多,具有明显规律性。另外,基于离线模型成功推断出下车站点的出行为1954.0 万人次,占总刷卡量69.5%,这将是构建“历史状态向量库”的根本。

图7 公交乘客一周出行次数分布Fig.7 Distribution of weekly trip times of bus passengers
就同一乘客群而言,重复出行频率越高,其规律性越强,下车站点推断概率就越大。图8列出了不同时间、空间粒度下周重复出行频率为1~4 次、≥5 次的人群占比。从一周情况看,偶发性出行占主体,高频出行人群随划分颗粒度增大而增多。若完全按照2.2.1节中K近邻状态向量(线路、站点)粒度,频率大于1 次的出行仅占17%,每天在固定线路和站点上、下车的人群并不多,可见若仅用K 近邻模型,会有较多出行因找不到“邻居”而无法推断下车站点。而按出行小区划分时,频率大于1次的出行比例升至31%,规律性明显增强。为此,要提升下车站点推断率,有必要在更大颗粒度去搜索潜在“邻居”。“基于出行小区估计”算法的时间复杂度为O(n2),通过分布式计算等,其单次平均搜索时间为1.26 ms,最大933 ms,计算时耗未见明显增加。

图8 不同颗粒度下周重复出行次数分布Fig.8 Distribution of repeated trips with different particle size
3.2 准确性分析
随机跟车抽查了2020年8月18日262 路、521路和527路等线路在不同班次、不同时段的车载人数,并与实时推断结果比较,如表2、图9和图10 所示。根据实测结果,各班次不同站段的车厢满载率与实际满载率基本吻合,能够反映公交运行过程中车厢拥挤水平变化;几个班次的断面平均车载人数的平均相对误差小于11%,部分班次误差仅为2%~3%,平均满载率的误差小于3 个百分点,可为后续日常监测及调度提供有效数据支撑。

表2 车厢满载率实时推断结果Table 2 Estimating bus load rate in real time
3.3 子模型耦合
统计各子模型的应用情况,“K 近邻模型”“出行小区估计”“先验概率分配”的推断数据占比分别为47%、21%和32%。3种算法相辅相成有机组合,有效提升了单一算法的推断率。

图9 521路某一班次实时推断结果Fig.9 Estimating result of line-521
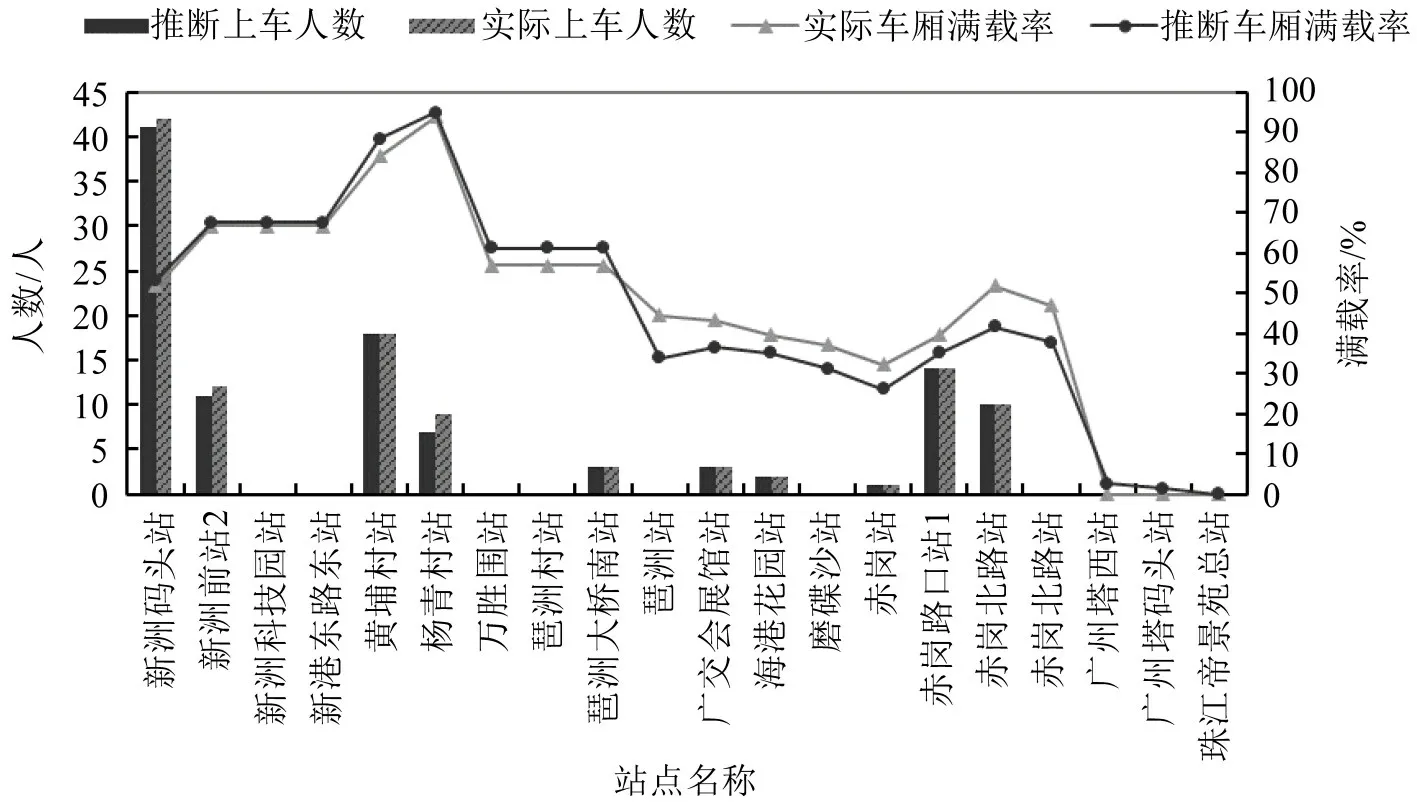
图10 262路某一班次实时推断结果Fig.10 Estimating result of line-262
4 结论
本文构建公交大数据驱动的“K 近邻+出行小区估计+先验概率分配”组合模型,实时推断所有电子支付乘客的出行OD,实现“一票制”支付情况下公交车厢满载率实时计算。提出了以K 近邻为核心的实时推断下车站点方法;并针对K近邻模型推断率过低等问题(仅占47%),研究了在更大空间维度分析乘客出行规律并推断下车站点,有效提升对历史数据的利用率和下车站点的推断率(增加约21个百分点);此外,针对偶发型乘客缺少历史规律数据的情况,充分利用站点下车客流量先验概率随机分配,实现电子支付乘客OD的全样本推断。抽样验证表明,所推断的单班次平均满载率误差在3个百分点以内,平均车载人数的误差小于11%。掌握实时车厢满载率,有助于公交管理部门深入了解每趟公交班次、每个公交断面的车厢拥挤度,为实时公交运营监测及调度优化提供决策辅助。
