轨迹数据驱动的单点信号交叉口运行效率评价方法

蔡晓禹，吕亮，卢凯明，唐小勇，高志刚

(1.重庆交通大学，a.交通运输学院，b.山地城市交通系统与安全重庆市重点实验室，重庆400074；2.重庆市城市交通大数据工程技术研究中心，重庆400020)

0 引言

信号交叉口运行效率评价是交叉口问题研判与方案优化的首要任务，交叉口供需平衡、整体及局部运行最优是交叉口运行效率评价的最终目标。采用省时、便捷、准确且可实施性强的评价方法，能够更好地辅助信号交叉口系统优化，支持交通管控方案的决策实施。

为多角度评价交叉口服务水平，学者利用多个指标进行综合评价。Igor Dakic[1]利用评价时段内绿灯到达车辆数占比，方向延误，连续周期内平均单位绿灯到达车辆占比3个指标评价自适应信号交叉口的运行效率。Xiaoyan ZHENG[2]等利用信息熵理论，选取平均延误、饱和度、排队长度作为主要指标。该类代表性研究的主要特点为：①数据主要来源于实测小样本数据，指标体系较为丰富，但同步获取难度大；②需要先确定不同服务水平下各评价指标的分级标准，我国现阶段对某些指标并没有相应的划分依据，而这是影响评价结果的重要因素。

随着传统浮动车数据(出租车、公交车GPS 数据)和车联网数据(滴滴、驾图等)不断汇集，围绕轨迹数据的指标估算方法不断产生。Huang J.[3]等通过定量分析非饱和状态下停车延误与车辆排队位置距交叉口停车线距离之间的函数关系，利用历史公交车GPS 轨迹数据构建了延误估计实用模型。Liu X.L.[4]等基于Hadoop 和MongoDB 对GPS 原始轨迹数据进行预处理并实现地图精准匹配，提出利用主曲线法估计交叉口转向延误。陈艳艳[5]提出一种新的基于浮动车停车点数据计算交叉口车辆排队长度的方法，能够推算出一个时间段内交叉口排队长度的平均值。何兆成[6]为弥补传统排队检测模型大多基于线圈检测器，模型假设过于理想化的缺陷，提出一种面向低采样率浮动车数据的信控交叉口最大排队长度检测方法，验证该方法在浮动车比率较高的主干路交叉口精度相对较高。

总体而言，信号交叉口运行效率评价主要分为4个阶段：第1阶段，主要靠人工统计交通参数，计算评价指标进行评价；第2阶段，主要依靠仿真，结合人工调查，实现信号交叉口运行评估；第3阶段，突破单指标评价的约束，从多角度全面评价交叉口运行效率，但更多地趋向于评价模型的套用，且数据来源仍主要以人工采集为主；第4阶段，以浮动车轨迹数据为例，利用交通大数据估算信号交叉口延误、排队长度两项核心指标，但并未针对交叉口服务水平评价提出一套完整的体系。因此，本文以出租车、公交车、驾图多源GPS轨迹数据为基础，从个体车辆交通参数提取入手，构建满足信号交叉口技术需求的客观、全面、可操作性强的评价方法体系。

1 轨迹数据特征

轨迹数据包含车辆唯一标识(ID)、坐标等信息，以重庆市主城区出租车、驾图、公交车3类轨迹数据为例，分别以15 s、10 s、1～15 s 为时间间隔稳定回传，原始关键字段如表1所示。

表1 GPS原始数据样例Table 1 GPS raw data sample

2 交通参数提取

2.1 原始数据预处理

(1)出租车、驾图GPS数据

利用SQL server 对原始数据进行清洗，借助ArcGIS平台获取待评价交叉口范围内轨迹数据，形成备用数据集。

(2)公交车GPS数据

公交车GPS数据缺少进、出站时间，下客流量等微观数据，故对公交车GPS数据进行如下分类处理。

情形1 交叉口附近无公交站，预处理方式与出租车GPS步骤类似。

情形2 交叉口附近有公交站，需筛选在交叉口范围不停车的公交车线路。公交线路与公交车牌(ID)无对应关系，故采取以下解决方案：

Step 1 选取研究时段(如6:00-18:00)通过指定交叉口的所有车辆ID集合。

Step 2 选取交叉口附近公交站发生停靠的所有车辆ID集合。

Step 3 求以上两者差集，得到交叉口附近停靠站不停车的车辆，形成公交车GPS数据集。

(3)有效样本集构建

不同信号方案下，不同停车次数对应轨迹速度序列变化特征规律有明显区别，基于此构建交叉口样本分类方法，利用Python对交叉口范围备用数据集进行批处理，并形成有效样本集。

2.2 个体车辆运行交通参数提取

(1)初始排队长度设停车线代表点的坐标为A(XLat0,YLong0)，车辆在进口道减速排队时，第1 个小于5 km·h-1的速度对应轨迹点为“初始停车点”，其坐标为B(XLat1,YLong1)，则两点间实际距离为

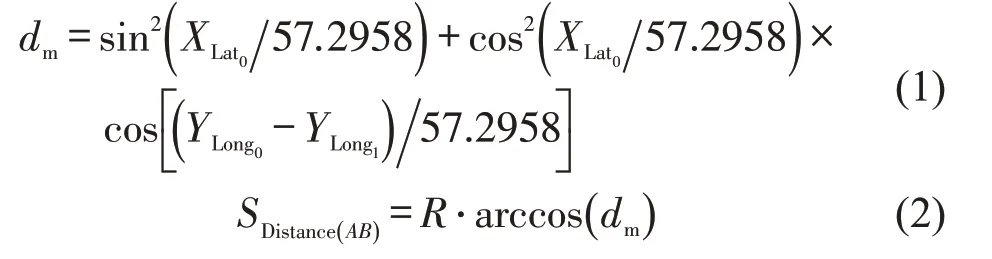
式中：R为地球的平均半径，取R≈6371.004 km

(2)通行时间

定义车辆初始停车点(V≤5 km·h-1)为通过交叉口起始时刻T0，当速度大于V0(根据不同的道路等级取值有所差异，默认为30 km·h-1)时，且不再发生减速、停车(即不出现速度小于等于5 km·h-1)，判定该轨迹点为“驶离轨迹点”，其回传时刻为T1，则车辆经过交叉口的通行时间T=T1-T0，利用“初始停车点”“驶离轨迹点”位置判别进口及转向。

(3)构建车辆运行参数信息表

针对交叉口有效样本集，提取各进口道不同转向样本车辆停车次数，初始排队长度，通行时间，形成车辆群体运行信息数据表，如表2所示。

3 交叉口运行效率评价指标构建

3.1 评价指标体系

利用多源轨迹数据，从交叉口车辆通行过程时间利用率，车道或进口空间利用率，两次停车车辆数表征的车道组(或进口道)饱和程度3 个角度出发，构建以综合运行指数为一级指标，交叉口平均通行时间，第95%分位排队长度，两次停车率为二级指标的评价指标体系，综合描述和评价交叉口运行状态和效率。

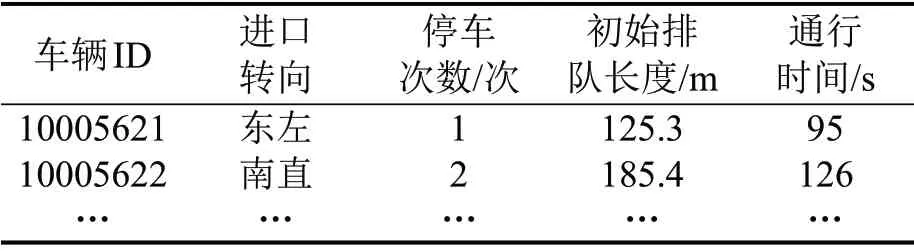
表2 车辆运行参数信息表Table 2 Information table of vehicle operating parameters

3.2 第2级评价指标计算方法

3.2.1 平均通行时间

本文重在利用有限代表性样本反映交叉口所有通过车辆总体运行水平，故以有效样本车辆为研究对象，计算车辆在交叉口平均通行时间为时间效率指标。计算方法为

式中：Ti为任意轨迹样本i的交叉口通行时间；n为评价时段内驶过交叉口的多源轨迹有效样本数。

3.2.2 第95%分位排队长度

图1为某交叉口平峰时段各进口道样本排队长度分布，单个进口道中，除少数离群点外，总体较为集中，不同进口道之间存在一定差异性。为尽量避免交叉口进口道上游个别异常停车点对最大排队长度产生误判，统一采用第95%分位排队长度作为最大排队长度。

图1 排队长度分布箱线图Fig.1 Queue length distribution box plot

3.2.3 两次停车率

常规定义两次停车率为交叉口发生两次停车车辆数与交叉口总过车数之比，但实际两者很难同时准确获取。多源轨迹数据仅占总过车数的15%～20%，且平峰和高峰有所差异；当轨迹样本数一定时，使用有效样本中两次停车样本数与总样本数比值衡量运行水平，易与总体产生较大误差。因此，本文将两次停车率定义为两次停车样本数占有效样本数的比例，用来表征饱和程度。

式中：q2为有效样本中两次停车样本数；qe为有效样本数。

4 综合评价指标及方法

4.1 综合评价指标模型构建

本文将平均通行时间，第95%分位排队长度，两次停车率进行融合，构建综合评价指标模型，模型结构为

式中：RI为综合评价指标(运行指数)，用来表征某进口道第j个转向、交叉口第j个进口道和整个交叉口的运行水平；当用来评价某转向时，m=1；当用来评价某进口道及整个交叉口时，m为某进口道转向数或交叉口进口道数。评价第j个转向或第j个进口道时，表示第j个转向样本平均通行时间(s)；当评价整个交叉口时，表示第j个进口道样本平均通行时间。Lj评价第j个转向或第j个进口道时，表示第j个转向样本第95%分位排队长度(m)；当评价整个交叉口时，表示第j个进口道样本第95%分位排队长度(m)。ψj评价第j个转向或第j个进口道时，表示第j个转向样本两次停车率；当评价整个交叉口时，表示第j个进口道样本两次停车率。Tmax为驾驶员可接受的最大通行时间(s)；Lmax为交叉口可接受的最大排队长度(m)；ψmax为可接受的最大两次停车率；W1为平均通行时间权重系数；W2为第95%分位排队长度权重系数；W3为两次停车率权重系数。

二级指标归一化处理时，充分考虑驾驶员可接受的最大交叉口通行时间，交叉口几何设计，相邻交叉口间距约束下可接受的最大排队长度，稳态运行下可接受的最大两次停车率等要素，实现从转向、进口、交叉口3个层次细化评价内容。

4.2 第2级评价指标权重系数确定

通过问卷调查3类出行群体对不同指标的敏感度及可接受度以确定权重，调查内容如图2所示。本次调查共回收342 个样本，其中，交管部门占比13%，环保部门占比8%，普通社会出行者占比79%。通过统计分析得知，通行时间对于不同群体敏感性均为最大。普通社会出行者对通行时间，排队长度，两次停车的敏感性依次递减；交管部门更重视对信号交叉口排队长度的控制；环保部门更关注车辆反复加、减速过程的排污程度，对两次停车的关注度略高于排队长度。

图2 调查问卷设计内容Fig.2 Questionnaire design content

为避免因调查群体占比不均匀引起的权重计算偏差，利用各群体样本分别计算出各评价指标的权重值，再取平均值作为最终各指标的权重，最终确定平均通行时间权重系数为0.435，第95%分位排队长度权重系数为0.291，两次停车率权重系数为0.274。

4.3 模型关键参数确定

(1)可接受最大排队长度Lmax

交叉口最小间距因满足红灯期间车辆最大排队长度，且进口道总设计长度中展宽渐变段长度和展宽段长度应满足《城市道路交叉口设计规程(2010版)》的要求。事实上，各类型交叉口受多种因素影响，对于不同类型交叉口范围取值难以统一划定。因此，参照规范中不同等级道路进口道展宽段与展宽渐变段长度设计值之和上限值作为可接受的最大排队长度。

(2)可接受最大通行时间Tmax

根据问卷调查结果显示，高峰时段开车经过一个信号交叉口可接受最大等待时间为2 min的样本占比最大，为33%。以自由流车速驶过交叉口范围的时间相比等待时间极小，因此将2 min 作为交叉口可接受的最大通行时间，即Tmax=2 min。

(3)可接受最大两次停车率ψmax

平峰时段交叉口通常不易发生大面积拥堵，运行状态相对比较稳定，认为该情形下交叉口运行处于可接受水平。选取4个典型信号交叉口，对平峰时段两次停车率进行统计分析，由图3各进口道统计分布可知，除少数进口道信号配时不合理，交通需求较大等可能原因致使两次停车率明显较大外，其余均小于0.3，且小于0.2的约占55%，因此，本文选取0.2作为可接受的最大两次停车率。

图3 平峰交叉口进口道两次停车率分布Fig.3 Two-stop rate distribution at entrance of flat peak intersection

5 服务水平等级划分

5.1 综合评价指标统计分析

计算上述4个典型交叉口不同分析时段的综合评价指标。图4为某交叉口3个时段内RI统计分布情况，早高峰1.49，平峰0.92，晚高峰1.85，可看出该运行指数具有一定的时变性，平峰与高峰相比总体运行效率较高，符合实际交通运行规律。

图4 典型信号交叉口3个时段RI 统计分布Fig.4 Statistical distribution of RI in three periods of typical signalized intersection

5.2 评价等级划分

通过大量综合评价指标计算及统计结果，基于高斯混合聚类模型对指标各等级区间阈值进行模糊划分。首先对降序排列的综合评价指标(165 条数据)进行聚类，类别数k分别取5和6两种情形，聚类效果如图5和图6所示。

图5 k=5 时聚类结果Fig.5 Clustering results when k=5

图6 k=6 时聚类结果Fig.6 Clustering results when k=6

由图5和图6可以看出：当k=5时，各区间阈值变化较均匀，除两端(RI小于0.7和大于2.0)变化较为明显，中间3 个类别RI以接近0.4 的梯度逐渐增大；当k=6时，RI大于1.5时被分成两个等级，且RI最大区间差值接近1，最小区间差值接近0.2，整体分布比较离散。结合表3可得，当RI大于2.0时，平均通行时间，第95%分位排队长度，两次停车率均远远超出各指标最大可接受水平，故已处于严重堵塞状态。因此，采用五级评价标准对交叉口的运行进行评价，参考HCM 评价标准给出对应服务水平下交通运行状态描述。

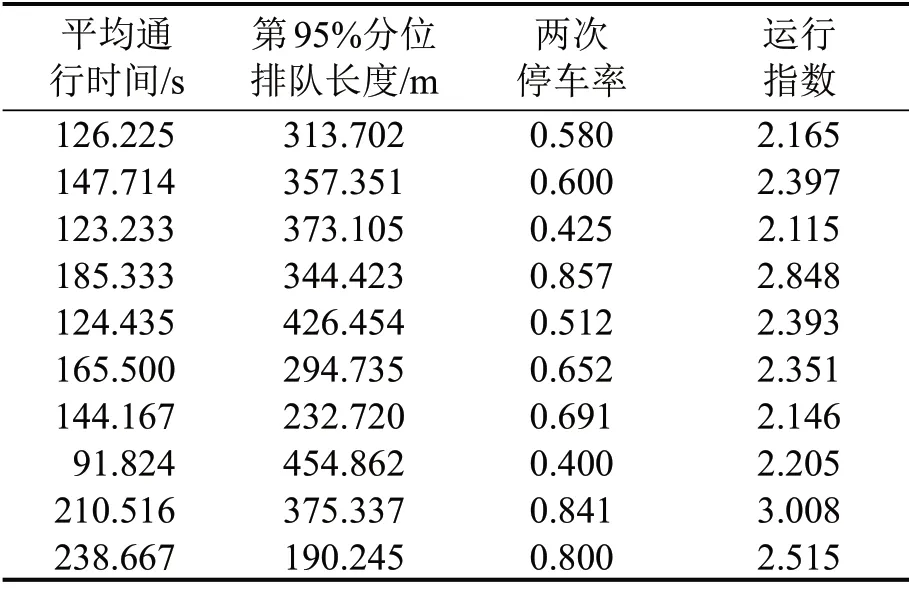
表3 二级评价指标及综合指标对应列表(RI＞2.0)Table 3 Corresponding list of secondary evaluation indicators and comprehensive indicators (RI＞2.0)

6 案例分析

6.1 基于VISSIM的交叉口运行仿真评价

为验证方法的技术可行性，选取重庆市巴南大道-渝南分流道信号交叉口进行交通流仿真。图7为仿真运行场景。

图7 VISSIM交通仿真模型Fig.7 VISSIM traffic simulation model

6.2 基于多源轨迹数据交叉口运行评价

对轨迹样本进行分类，计算得到有效样本运行交通参数信息。该交叉口为主路与主路相交路口，参照规范，可接受最大排队长度为140 m，最大通行时间为120 s，最大两次停车率为0.2。从而得到转向级、进口道级、交叉口级评价指标结果及相应服务水平。表4为早高峰评价结果样表。

6.3 评价结果对比分析

6.3.1 最大排队长度

将本文估算的最大排队长度，仿真检测的最大排队长度与实际调查结果进行对比。实测最大排队长度由最大排队车辆数乘以平均车间距计算而得，平均车间距为车身长与安全停车间距之和，停车间距受道路条件(坡度)、驾驶员特性、车辆性能等因素影响，且实例分析中的道路存在较大纵坡，且不同车辆类型占比也不确定，因此通过查阅相关文献[7-8]，本文取6.5 m。统计得到3 个时段各进口直行、左转最大排队长度对比结果如图8～图10所示，主要特征可归纳为以下几点：

(1)本文估测值与实际值相比略小，且在平峰、高峰误差相对比较均匀，误差在10%～20%。

(2)仿真总体比实际值偏大，在过饱和(饱和度大于1)时，偏大程度更加明显，这是因为仿真过程车辆静态路径选择时在交叉口进口道易产生异常停车、换道行为，夸大排队覆盖范围。如晚高峰仿真平均相对误差为72.5%，本文为9.8%，仿真误差明显偏大。

表4 本文方法评价结果(早高峰)Table 4 Evaluation results of this method(morning peak)

(3)低饱和度下(如平峰时段)仿真和本文提取的最大排队长度与实测值误差均较小。平峰时提取结果平均相对误差均接近15%。

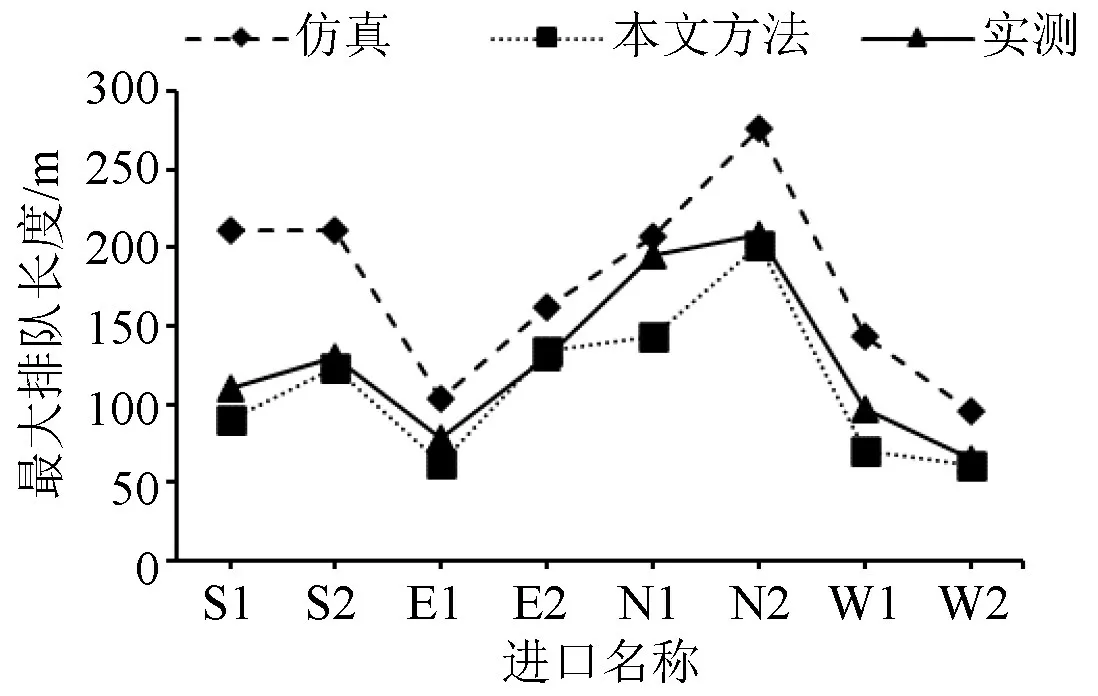
图8 早高峰最大排队长度对比Fig.8 Comparison of maximum queue length in morning peak

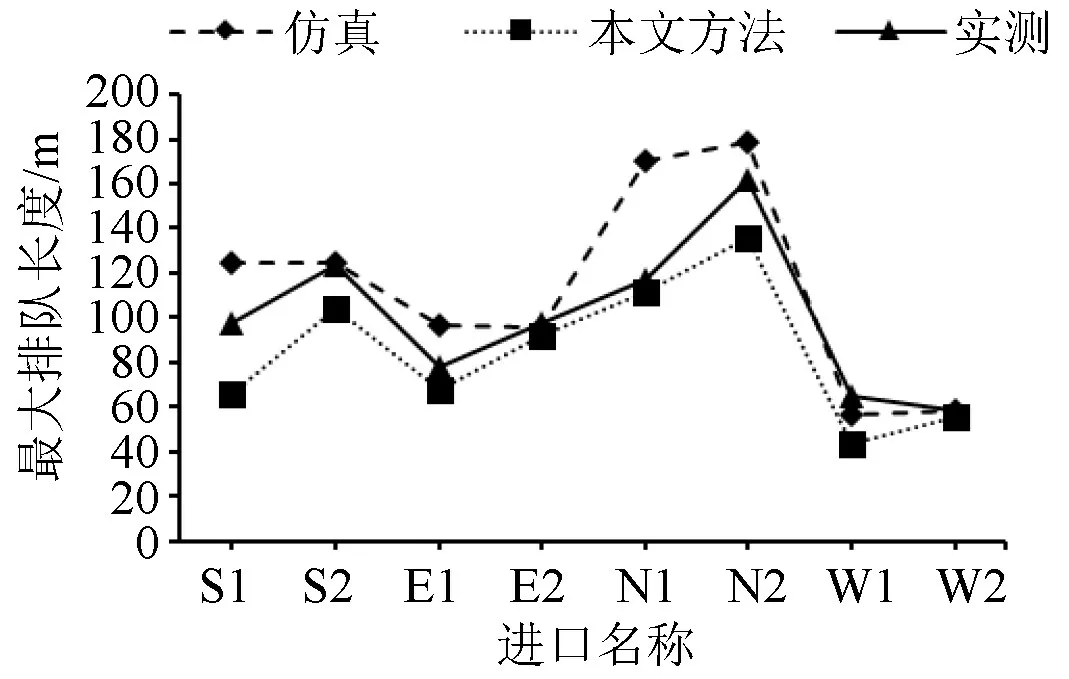
图9 平峰最大排队长度对比Fig.9 Comparison of maximum queue length of flat peak

6.3.2 服务水平

表5为采用仿真与本文方法得到的服务水平评价结果，两种方法评价指标和标准均不同，故将评价结果与实际观测交通运行状态进行对比分析。主要可归纳为以下几点：

(1)对比不同转向服务水平可知，两种方法的评价结果总体趋势基本一致。如早高峰南进口直行和左转仿真评价结果为C级和E级，本文方法评价结果为A级和B级，而实际情况由于左转通行能力不足，运行效率较直行明显偏低，表明两种方法均对交通状态具有敏感性。

图10 晚高峰最大排队长度对比Fig.10 Comparison of maximum queue length in evening peak

(2)低饱和度下(如平峰时段)，仿真与实际运行水平的偏差较小，且与本文评价结果比较接近。过饱和情形下，仿真因异常停车、排队使停车延误明显增加，服务水平降低。如晚高峰各进口均处于过饱和状态，仿真评价结果与实际偏差明显较大。

(3)仿真评价结果会掩盖不同流向失衡现象，本文方法评价结果更符合实际。如早高峰、平峰东进口直行和左转车流，仿真评价均处于D级及以上水平，属非稳定或拥堵状态；本文方法评价结果能够反映左转明显劣于直行运行水平。

(4)多源轨迹样本量的多少会显著影响本文方法的评价结果。当有效样本量较少时，评价结果会优于实际交通运行水平。如早高峰、平峰北进口左转服务水平的评价结果均比实际运行水平乐观。

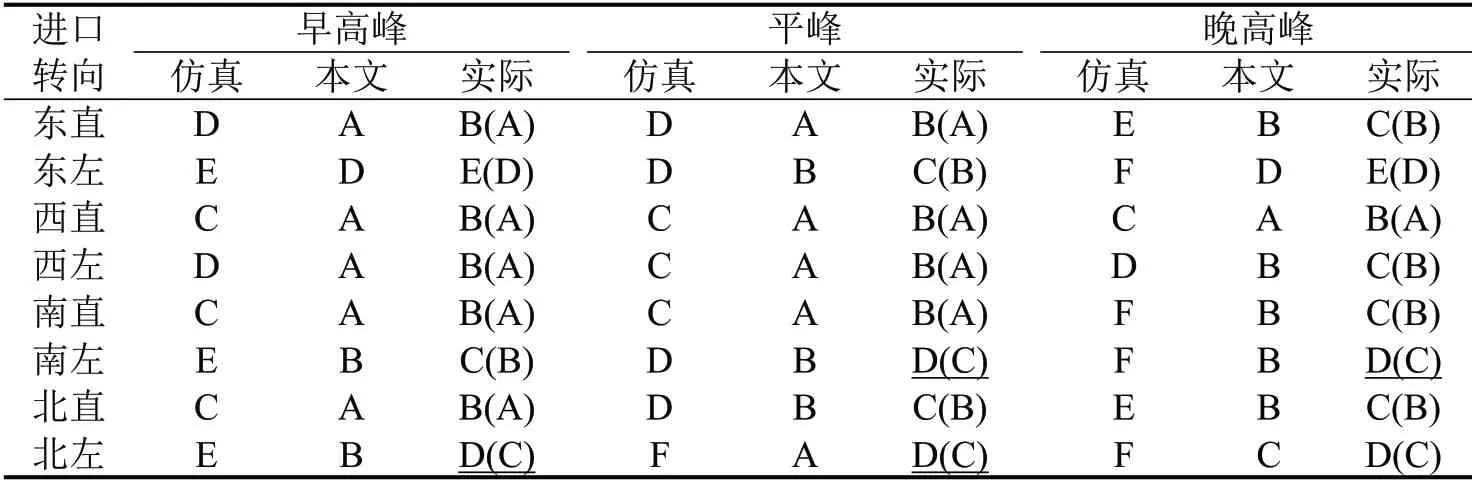
表5 服务水平对比表Table 5 Service level comparison table

7 结论

本文对原始多源轨迹数据进行处理分类，构建面向交叉口不同转向、不同进口方向及交叉口整体的综合评价模型。选取重庆市典型干线信号交叉口进行评价，得到以下结论：

(1)当评价时长为2 h 时，能够从转向、进口、交叉口3 个层次较为准确地评价信号交叉口运行效率。

(2)在过饱和情形下(饱和度大于1)，本文方法明显优于仿真，更贴近实际交通运行状态；非饱和情形下，本文方法和仿真评价结果与实际运行状态均比较接近。

(3)样本量充足时，评价结果较为准确，当部分转向有效样本量不足时，本文方法会明显影响评价结果准确度。