比特币区块链的数据压缩

2021-02-27陈晓姣林宪正俞能海

网络与信息安全学报 2021年1期

陈晓姣，林宪正，俞能海

比特币区块链的数据压缩

陈晓姣1,2，林宪正1,2，俞能海1,2

（1. 中国科学技术大学网络空间安全学院，安徽合肥 230001；2. 中国科学院电磁空间信息重点实验室，安徽合肥 230001）

区块链技术为数据存储提供了一种透明、不可更改、去中心化的方法。但随着数据量不断增加，比特币区块链系统需要大量的存储空间。分析了比特币区块的结构，针对比特币交易中的部分字段，提出相应的编码方案来减小比特币区块体积。实验表明，所提方案可使区块链体积减小18.13%。

区块链；压缩；熵；编码

1 引言

区块链技术首次出现在比特币研究[1]中，被用来实现分布式共识以及防止双重花费。区块链由一组节点使用共识协议（如工作量证明、权益证明、代理权益证明）维护[2]。每个全节点在本地存储完整区块链的复制，因此全节点可独立完成交易查找、账户余额计算等工作[3]。然而，随着比特币区块链包含的数据量不断增加，区块链体积不断增大。例如，截至2019年12月，比特币区块链约占存储空间260 GB。比特币区块链体积过大演变为可伸缩性问题[4]，导致空白节点同步时间增长。同时，繁重的存储负担会增加维护全节点的成本，从而导致愿意成为全节点的节点数目减少。相应地，区块链系统会被少数的全节点掌控，这与区块链的去中心化思想相违背。

本文提出一种减小比特币区块链体积的方法。在分析比特币区块结构的前提下，针对比特币交易中的特定字段，本文提出相应的编码方案减小交易体积，从而减小比特币区块体积。

2 相关工作

随着区块链数据不断增多，减小区块链区块体积方面的研究不断增加。在比特币白皮书中，Nakamoto[1]提出：一旦最近的交易被纳入足够多的区块中，就可以丢弃它之前的交易数据，以节省硬盘空间。由于Merkle根被包含在区块哈希中，该树的分支被清除后，并不会影响区块的哈希数据。Géraud等[5]提出基于图和格基约减技术的交易删除方法。Bruce[6]提出迷你区块链策略，最新的部分区块链被保留，旧的交易则被删除，因为账户树维护了所有非空地址的余额平衡，所以不会影响账户余额平衡和钱币归属。Palai等[7]提出了区块摘要，一个区块摘要可以看成包含它所有子区块输入以及未花费输出的大型单笔交易。Nadiya等[8]提出基于比特币区块链的区块摘要生成方法。Dorri等[9]提出一种存储优化的区块链来使物联网用户移除它们旧的交易。Ateniese等[10]提出一种可重写区块链，任意数量的区块可以被重写并压缩成较少的区块。Rajasekhar等[11]提出基于比特币的区块可重写方法。Marsalek等[12]提出一种双链结构，使空白轻量节点可以下载更少的数据量完成同步。Kim等[13]提出一种基于实用拜占庭容错（PBFT，practical Byzantine fault tolerance）的存储压缩共识算法，该算法可减小轻量节点所需存储的区块链体积。Boneh等[14]提出一种新的多重签名策略来进行签名压缩和公钥聚合，从而减小比特币区块体积。

一些研究尝试将整个区块链分成块存储在不同的节点中，以减小单个节点的存储压力。Perard等[15]提出基于纠删码的区块链数据编码方法。区块可以被编码成分片存储在不同的节点中，同时可以从这些节点下载分片以恢复原先的区块。Dai等[16]提出一种类似的网络编码方法。Abe等[17]提出一些存储资源受限的节点组成集群，每个节点存储由分布式哈希表（DHT，distributed hash table）算法得到的部分区块链数据。同时，这些节点共同协作来验证新的交易以及区块。Xu[18]提出了section-blockchain，其中，每个节点都是平等的并且共同对网络作出贡献。每个节点只需要存储区块头、一些区块链分片以及数据库闪照，并且不会影响整个区块链的安全性。Liu等[19]提出一种双链策略，使没有足够存储空间的节点可以把数据存储在其他节点。Mei等[20]提出一种基于余数系统的存储优化方法来减小每个节点的存储量。Mcconaghy等[21]提出一种结合区块链和现有分布式数据库特性的可伸缩的区块链数据库。

Poon等[22]提出闪电网络。闪电网络实现了在离线环境下提供比特币交易的方式，在支付通道打开后，参与方可离线发生任意数量的交易，而无须广播到比特币的网络上，从而大大提高了交易速度，减轻了比特币网络的压力。当支付通道关闭后，将交易的最终版本广播到网络中，从而减小总的交易体积。Decker等[23]提出一种双向小额支付渠道，支持小额支付渠道自动更新，确保了端到端安全。

Pontiveros等[24]提出以太坊区块链的压缩方法。由于以太坊中的智能合约倾向使用相似的字节码结构，他们提出将一种伪操作码作为指针指向前一个智能合约中相同字节码的位置。王守道等[25]提出了类似的操作码来压缩以太坊中的智能合约。Zheng等[26]提出基于星际文件系统（IPFS，inter-planetary file system）的区块链存储模型。具体的交易数据被存储到IPFS系统中，只有IPFS哈希被打包到区块中。Norvil等[27]提出类似的借助于IPFS系统减小以太坊区块链的方法。

一些研究主要围绕减小区块链中交易的体积。在隔离见证[28]中，见证树用来存储交易中的脚本以及签名，而不影响整个交易的效果。在可变交易[29]中，交易的结构被重构，因此可以删除其中无用的字段。在Lumino交易压缩协议[30]中，同一个用户的不同交易间可以采用增量压缩来减小体积。Zima[31]提出用交易哈希前缀取代完整哈希以及可变长字节数表示输出索引，从而减小交易输入的体积。

3 方案设计

3.1 比特币区块结构

比特币区块数据以网格格式存储在磁盘上，单个文件不超过128 MB，每个文件中存储若干个区块。比特币区块之间由4 byte的魔数（0xD9B4BEF9）分隔。接下来是区块大小（4 byte），表示单个区块的体积。一个完整的比特币区块由区块头和区块体组成。区块头占80 byte，包含以下信息：版本号（4 byte）、前一区块的哈希值（32 byte）、Merkle树的根哈希值（32 byte）、时间戳（4 byte）、目标值（4 byte）、随机数（4 byte）。区块体包含交易信息，这些交易构成Merkle树，Merkle树的树根值存储在区块头中。每个区块的第一笔交易是coinbase交易，这是一笔为了让矿工获得奖励及手续费的特殊交易。一笔完整的比特币交易结构如图1所示，包含版本号（4 byte）、若干输入、若干输出以及锁定时间（4 byte）。交易输入包含引用交易哈希（4 byte）、引用交易输出索引（32 byte）、输入脚本信息以及序列号（4 byte）。交易输出由比特币数量（8 byte）以及输出脚本信息组成。一笔交易中的每个输入对应引用的之前一笔交易的一个输出，该对应关系通过交易输入中的引用交易哈希以及引用交易输出索引表示。比特币区块主要由交易信息组成，且改变区块头内部字段会导致区块哈希变化，因此本文主要考虑比特币区块内交易的压缩。

3.2 编码方案

本节基于对真实比特币区块数据的统计分析，提出相应的编码方案。使用Bitcoin Core客户端下载区块链，下载时间为2019年12月27日15时19分，共609 973个区块。熵可衡量平均信息量，计算如式(1)所示。其中，指概率空间中所有可能的样本，x指该样本出现的概率。

Figure 1 Composition of a bitcoin transaction

3.2.1 版本号

交易版本号占4 byte，表示该交易遵循的规则。统计数据包含487 589 740笔交易。其中，87.89%的交易版本号为1，12.11%的交易版本号为2，仅6笔交易使用其他版本号。根据式(1)，计算得到熵为0.53 bit。编码后，绝大多数版本号可用1 byte表示，当无法用1 byte表示时，采用5 byte表示，第一个字节置为0xFF，后4 byte保持不变。

3.2.2 引用交易哈希

交易输入中的引用交易哈希占32 byte，用来指代所引用的交易。新编码方案共40 bit，其中，前20 bit表示引用交易所在的区块高度，后20 bit表示引用交易在区块内的索引。创世区块的区块高度为0，每个区块中coinbase交易的交易索引为0。目前，比特币区块高度约600 000，用20 bit足够表示。同时，统计数据中单个比特币区块中最大交易数量为12 239，20 bit足够表示。

3.2.3 引用交易输出索引

交易输入中引用交易输出索引占4 byte，表示引用输出在引用交易中的位置。统计数据中最大的交易输出数量为13 107，可用14 bit表示。根据式(1)，计算得到熵为1.26 bit。编码后，输出索引可用1 byte或2 byte表示。前2 bit为00时，后6 bit表示输出索引，可表示0~63，前2 bit为11时，2字节中的后14 bit表示输出索引。

3.2.4 序列号

交易输入中序列号占4 byte，用来覆盖在交易锁定时间之前失效的交易。统计数据中包含1 196 011 166个序列号，其中，78.10%为0xFFFFFFFF，18.57%为0xFFFFFFFE，2.91%为0xFFFFFFFD。根据式(1)，计算得到熵为0.92 bit。编码后，序列号可用1 byte或5 byte来表示。当第1字节为0xFF、0xFE、0xFD时，分别表示0xFFFFFFFF、0xFFFFFFFE、0xFFFFFFFD这3种情况；当第1字节为0时，表示之后的4 byte为完整的序列号。

3.2.5 比特币数量

交易输出中比特币数量占8 byte。统计数据中包含1 298 644 580个比特币数量。从图2可以看出，比特币数量集中在106聪。根据式(1)，计算得到熵为20.72 bit。编码方案根据第1 byte（<0xFD,=0xFD,=0xFE,=0xFF）可将编码方案分为1 byte，3 byte，5 byte，9 byte。经过统计，3.29%的比特币数量用1 byte表示，14.64%的用3 byte表示，80.86%的用5 byte表示，1.21%的用9 byte表示。

图2 比特币数量分布

Figure 2 Distribution of bitcoin amount

3.2.6 锁定时间

交易中锁定时间占4 byte，表示该交易能被加到区块链中最早的时间。统计数据中83.36%的锁定时间为0，表示立即执行。如果锁定时间小于或等于5亿，则该字段表明区块高度，表明该交易在指定区块高度前不会被包含在区块链中。如果锁定时间大于5亿，则为UNIX时间戳（从1970年1月1日以来的秒数），表明该交易在指定时间点前不会被包含在区块链中。根据式(1)，计算得到熵为3.55 bit。编码后，锁定时间为0时，用1 byte表示，其余用5 byte表示，其中，第1个字节置为0xFF，其余保持不变。

3.3 压缩算法

每个区块中的coinbase交易不进行压缩。该压缩算法包含比特币交易中6个字段的编码替换，其中，在替换引用交易哈希字段前，需先查询该引用交易所在区块高度及其块内索引，具体算法如算法1所示。[]表示高度在的区块。REP([],tx.version,encode(tx.version))表示用编码后的版本号替换原先的版本号，INQ(in.hash,A)表示根据交易输入中引用交易哈希查询得到引用交易所在的区块高度以及该交易在块内的索引。

算法1 压缩算法

输入比特币区块链，区块数量

输出压缩后的区块链

3.4 解压缩算法

与压缩算法类似，该解压缩算法包含比特币交易中6个字段的解码替换，其中，在替换编码后的引用交易哈希字段前，需先计算引用交易哈希，具体的解压缩算法如算法2所示。REP(D[], tx.version,decode(tx.version))表示用解码后的版本号代替之前编码的版本号，T←FIND (in. newindex, D)表示根据交易输入中的新指针找到引用交易的内容。由于解压缩过程是从前往后依次进行，此时查找到的引用交易已经解压完成，其交易哈希可对其内容直接进行两次SHA256运算得到。

算法2 解压缩算法

输入压缩后的区块链，区块数量

输出解压后的区块链

4 实验

首先，将算法1应用于区块链文件blk00004测量压缩时延，该文件包含6 395个区块，1 675 996笔交易。算法1中INQ功能通过构建本地数据库完成。该实验在配置为2.2 GHz Intel Xeon Gold 5120T中央处理器以及32 GB 2400 MHz DDR4内存的服务器上完成。文件blk00004的初始大小为131 041 kB，压缩后大小为108 146 kB，相应的压缩率为82.53%，压缩时间为140 s。之后，将算法1应用于获取的完整比特币区块链，包含609 973个区块，487 589 740笔交易。图3表示压缩率随压缩的区块个数的变化。当压缩的区块个数较小时，压缩率不稳定，随着区块个数逐渐增大，压缩率趋近于81.87%，表明该压缩方案可减小比特币区块链体积18.13%。图4表示压缩率与区块中包含交易笔数的关系。当一个区块只包含一笔交易时，该交易为coinbase交易，无法压缩。由于区块头仅占据80 byte，当单个区块中包含的交易笔数逐渐增大时，它对压缩率的影响可以忽略。如图4所示，大多数区块的压缩率接近81%。

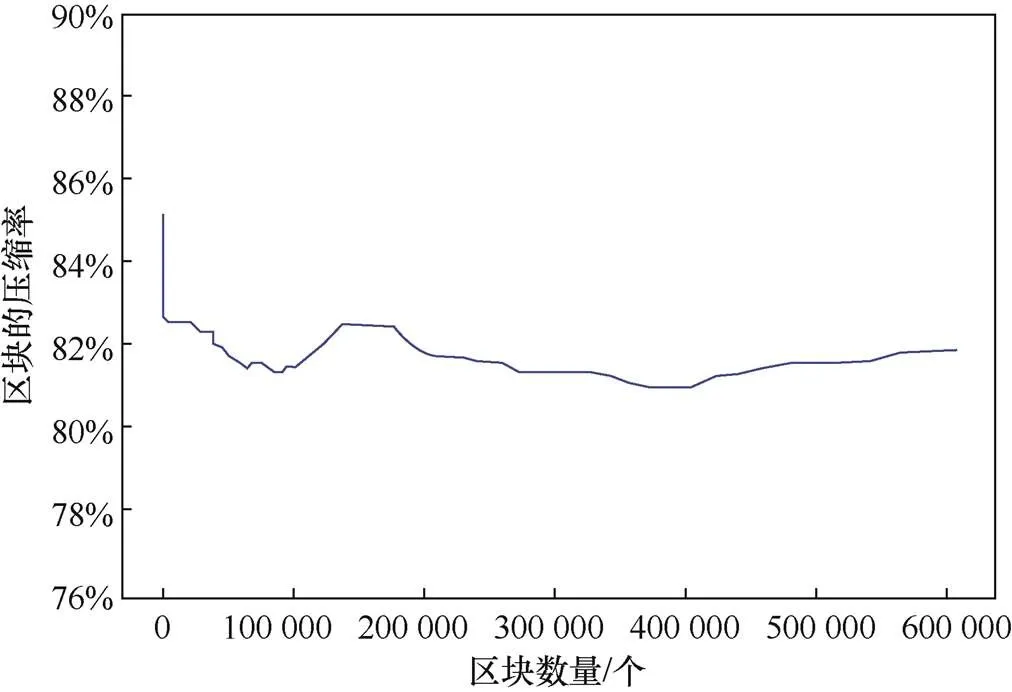
图3 压缩率随区块数量变化

Figure 3 Compression rate of various numbers of bitcoin blocks

图4 压缩率随交易数量变化

Figure 4 Compression rate of bitcoin blocks containing various numbers of transactions

5 本文方案的应用

5.1 在空白节点同步中的应用

如图5所示，本文方案可用于减小空白节点同步时所需带宽。当新的空白节点加入网络，该节点需从全节点下载区块链数据。全节点首先将比特币数据进行压缩再进行传输。当节点接收到全部数据后，对数据进行解压缩，恢复出完整的区块链数据并保存在本地。

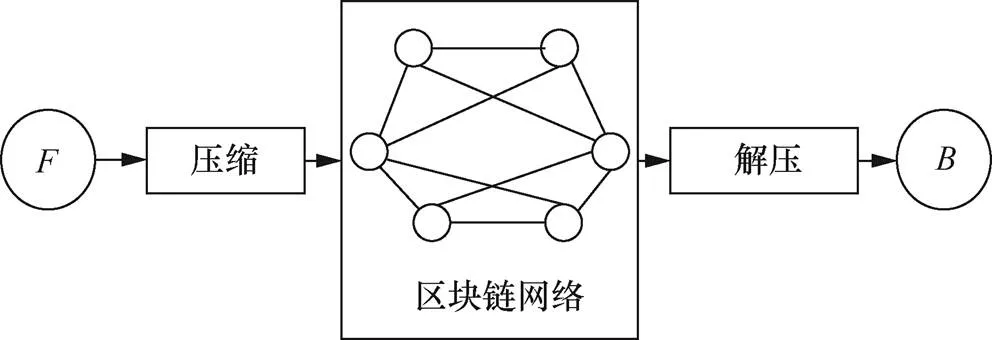
图5 空白节点同步

Figure 5 Blank node synchronization

5.2 在本地存储中的应用

如图6所示，全节点可采用算法1减小本地所需的区块链存储空间。考虑到分叉的可能，保留最新的6个区块不进行压缩。它维护了交易池和未花费交易输出（UTXO，unspent transaction output）集合，在进行压缩存储前，对需压缩的区块链进行扫描，确保UTXO集合的正确性，之后和普通全节点一样，使用现有比特币协议查询本地信息，对新交易以及新区块进行验证，完成共识，且不会带来额外开销。同时，简易支付验证（SPV，simplified payment verification）节点可以从节点获取足够信息来验证交易。

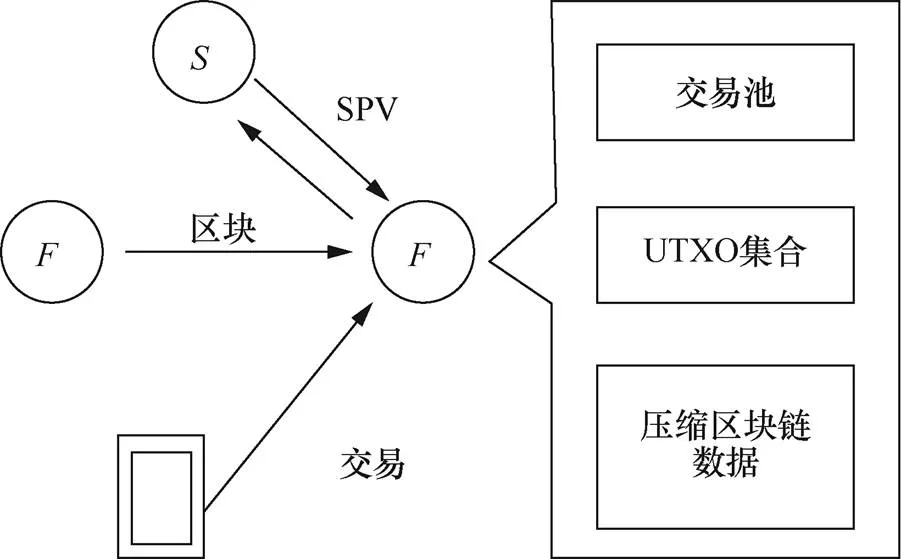
图6 全节点本地存储

Figure 6 Local storage of a full node

5.3 交易哈希计算

在比特币区块链中，交易哈希被用来构建Merkle树。交易哈希由对交易内容进行两次SHA256运算得到Hash←SHA256（transaction content）。由于算法1更改了交易内容，交易哈希无法直接根据其内容进行哈希运算得到。必须先恢复其交易内容，才可以进行哈希计算。由于coinbase交易未被压缩，必须追溯到与该交易相关的所有coinbase交易来恢复交易内容。

如算法3所示，压缩后的交易哈希计算主要由两步组成。首先，所有与该交易相关的交易输入在栈1的辅助下被压入栈2中，这个过程类似于叉树的遍历，它的叶子节点是所有与之相关的coinbase交易。然后，栈3用来存储每一步中恢复出的哈希值。最后，恢复出完整的交易内容，其哈希可直接进行两次SHA256运算得到。其中，S1.push(E.inputs.newindex)表示将交易中所有输入中的新交易哈希索引压入栈1中。←FIND()表示根据交易输入中的新哈希索引找到与之对应的交易内容。hash←CALHASH(,3,T.inputsnum)表示根据交易中交易输入的数量，从栈3中弹出相应数量的交易哈希进行替换，同时对交易中编码压缩的部分进行相应解码替换，然后对补全的交易进行两次SHA256运算得到哈希值。3.pop(T.inputsnum)表示栈3执行与交易输入数量对应的弹出操作。

算法3 交易哈希计算算法

输入压缩后的交易

输出交易哈希

5.4 SPV中的验证过程

SPV节点是一种只存储区块头的轻量节点，该类型节点需要从全节点获取足够信息来完成交易验证，信息包括一条连接交易哈希与区块头中Merkle根哈希的Merkle路径。SPV获取该信息后，根据Merkle路径计算当前待验证交易所在区块的Merkle根哈希，然后与本地存储的区块头信息进行比较，从而定位到待验证交易所在的区块位置。如果该交易所在区块的区块深度至少为6，则认为该交易是有效的。由于上述压缩算法更改了交易内容，每个交易哈希都需通过算法3来构建Merkle路径。

6 结束语

本文在分析比特币区块结构的前提下，针对比特币交易中部分字段提出相应编码方案，减小比特币交易体积，从而减小比特币区块链体积。在未来工作中，将会提出一种基于上述编码方案的新区块链构建方案，该方案可解决由哈希指针引起的碰撞问题。例如，在比特币区块链中，两笔coinbase交易（分别位于块91 812和块91 842）有相同的交易哈希。这就导致依靠现有的比特币协议无法解决这两笔交易的“双花”问题。同时该方案可拓展为通用的区块链存储改进方案，使用指针替换区块链中重复出现的数据内容，并可对定长字段进行数据统计，若计算所得熵小于定长，则可考虑用可变长编码替换。

[1]NAKAMOTO S. Bitcoin: a peer-to-peer electronic cash system[R]. 2008.

[2]章峰, 史博轩, 蒋文保. 区块链关键技术及应用研究综述[J]. 网络与信息安全学报, 2018, 4(4): 22-29.

ZHANG F, SHI B X, JIANG W B. Review of key technology and its application of blockchain[J]. Chinese Journal of Network and Information Security, 2018, 4(4): 22-29.

[3]沈鑫, 裴庆祺, 刘雪峰. 区块链技术综述[J]. 网络与信息安全学报, 2016, 2(11): 11-20.

SHEN X, PEI Q Q, LIU X F. Survey of block chain[J]. Chinese Journal of Network and Information Security, 2016, 2(11): 11-20.

[4]XIE J, YU F R, HUANG T, et al. A survey on the scalability of blockchain systems[J]. IEEE Network, 2019, 33(5): 166-173.

[5]GÉRAUD R, NACCACHE D, ROŞIE R. Twisting lattice and graph techniques to compress transactional ledgers[C]//International Conference on Security and Privacy in Communication Systems. 2017: 108-127.

[6]BRUCE J D. Purely P2P crypto-currency with finite mini-blockchain[R]. 2013.

[7]PALAI A, VORA M, SHAH A. Empowering light nodes in blockchains with block summarization[C]//2018 9th IFIP International Conference on New Technologies, Mobility and Security (NTMS). 2018: 1-5.

[8]NADIYA U, MUTIJARSA K, RIZQI C Y. Block summarization and compression in bitcoin blockchain[C]//2018 International Symposium on Electronics and Smart Devices (ISESD). 2018: 1-4.

[9]DORRI A, KANHERE S S, JURDAK R. MOF-BC: a memory optimized and flexible blockchain for large scale networks[J]. Future Generation Computer Systems, 2019, 92: 357-373.

[10]ATENIESE G, MAGRI B, VENTURI D, et al. Redactable blockchain or rewriting history in bitcoin and friends[C]//2017 IEEE European Symposium on Security and Privacy (EuroS&P). 2017: 111-126.

[11]RAJASEKHAR K, YALAVARTHY S H, MULLAPUDI S, et al. Redactable blockchain and it's implementation in bitcoin[J]. International Journal of Engineering & Technology, 2018, 7(1): 401-405.

[12]MARSALEK A, ZEFFERER T, FASLLIJA E, et al. Tackling data inefficiency: compressing the bitcoin blockchain[C]//2019 18th IEEE International Conference on Trust, Security and Privacy in Computing And Communications/13th IEEE International Conference on Big Data Science and Engineering (TrustCom/BigDataSE). 2019: 626-633.

[13]KIM T, NOH J, CHO S. SCC: storage compression consensus for blockchain in lightweight IoT network[C]//2019 IEEE International Conference on Consumer Electronics (ICCE). 2019: 1-4.

[14]BONEH D, DRIJVERS M, NEVEN G. Compact multi-signatures for smaller blockchains[C]//International Conference on the Theory and Application of Cryptology and Information Security. 2018: 435-464.

[15]PERARD D, LACAN J, BACHY Y, et al. Erasure code-based low storage blockchain node[C]//2018 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData). 2018: 1622-1627.

[16]DAI M, ZHANG S, WANG H, et al. A low storage room requirement framework for distributed ledger in blockchain[J]. IEEE Access, 2018, 6: 22970-22975.

[17]ABE R, SUZUKI S, MURAI J. Mitigating bitcoin node storage size by DHT[C]//Proceedings of the Asian Internet Engineering Conference. 2018: 17-23.

[18]XU Y. Section-Blockchain: a storage reduced blockchain protocol, the foundation of an autotrophic decentralized storage architecture[C]//2018 23rd International Conference on Engineering of Complex Computer Systems (ICECCS). 2018: 115-125.

[19]LIU T, WU J, LI J, et al. Secure and balanced scheme for non-local data storage in blockchain network[C]//2019 IEEE 21st International Conference on High Performance Computing and Communications, IEEE 17th International Conference on Smart City, IEEE 5th International Conference on Data Science and Systems (HPCC/SmartCity/DSS). 2019: 2424-2427.

[20]MEI H, GAO Z, GUO Z, et al. Storage mechanism optimization in blockchain system based on residual number system[J]. IEEE Access, 2019, 7: 114539-114546.

[21]MCCONAGHY T, MARQUES R, MÜLLER A, et al. BigchainDB: a scalable blockchain database[R]. 2016.

[22]POON J, DRYJA T. The bitcoin lightning network: scalable off-chain instant payments[R]. 2016.

[23]DECKER C, WATTENHOFER R. A fast and scalable payment network with bitcoin duplex micropayment channels[C]//Symposium on Self-Stabilizing Systems. 2015: 3-18.

[24]PONTIVEROS B B F, NORVILL R, STATE R. Recycling smart contracts: compression of the ethereum blockchain[C]//2018 9th IFIP International Conference on New Technologies, Mobility and Security (NTMS). 2018: 1-5.

[25]王守道, 蒋玉明, 胡大裟. 基于区块链的智能合约压缩存储方法[J]. 现代计算机, 2019(9): 42-46.

WANG S D, JIANG Y M, HU D S. Smart contract compression storage method based on blockchain[J]. Modern Computer, 2019(9): 42-46.

[26]ZHENG Q, LI Y, CHEN P, et al. An innovative IPFS-based storage model for blockchain[C]//2018 IEEE/WIC/ACM International Conference on Web Intelligence (WI). 2018: 704-708.

[27]NORVILL R, PONTIVEROS B B F, STATE R, et al. IPFS for reduction of chain size in Ethereum[C]//2018 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData). 2018: 1121-1128.

[28]LOMBROZO E, LAU J, WUILLE P. BIP 141: segregated witness[R]. 2015.

[29]ZANDER T. Flexible transactions[R]. 2016.

[30]LERNER S D. Lumino transaction compression protocol(LTCP)[R]. 2017.

[31]ZIMA M. Inputs reduction for more space in bitcoin blocks[C]//2018 Crypto Valley Conference on Blockchain Technology (CVCBT). 2018: 112-115.

Compression of bitcoin blockchain

CHEN Xiaojiao1,2, LIN Xianzheng1,2, YU Nenghai1,2

1. School of CyberScience, University of Science and Technology of China, Hefei 230001, China 2. Key Laboratory of Electro-magnetic Space Information, Chinese Academy of Sciences, Hefei 230001, China

The blockchain provides an immutable, transparent, and decentralized method for data storage. However, as the volume of data gradually increases, the public blockchain system requires significant storage space. The bitcoin block's structure was analyzed. A method was introduced to compress the size of transactions in the bitcoin blockchain by encoding specific fields. Experiment shows that the proposed method can reduce the storage space of the bitcoin blockchain by 18.13%.

blockchain, compression, entropy, encode

TP311

10.11959/j.issn.2096−109x.2021008

2020−01−14；

2020−03−18

林宪正，sjlin@ustc.edu.cn

安徽省自然科学基金（BJ2100330001）

The Natural Science Foundation of Anhui Province, China (BJ2100330001)

陈晓姣, 林宪正, 俞能海. 比特币区块链的数据压缩[J]. 网络与信息安全学报, 2021, 7(1): 76-83.

CHEN X J, LIN X Z, YU N H. Compression of bitcoin blockchain[J]. Chinese Journal of Network and Information Security, 2021, 7(1): 76-83.

陈晓姣（1995− ），女，江苏镇江人，中国科学技术大学硕士生，主要研究方向为区块链。