UHMWPE基水润滑尾轴承润滑特性仿真及试验研究*

2021-02-27王艳真李虎林尹忠慰

润滑与密封 2021年2期

王艳真李虎林钟涛尹忠慰

(1.中国船舶及海洋工程设计研究院上海 200011;2.上海交通大学设计学院上海 200240)

水介质具有来源广泛、零污染、安全、阻燃、摩擦因数低、黏温特性稳定以及冷却效果好等一系列优点，是一种极具发展潜力的润滑介质。近年来，以水作为润滑介质的尾轴承在船舶上开始被广泛应用。目前，水润滑尾轴承材料一般为高分子聚合物，该类材料硬度低、弹性模量小，加之尾轴承低速的运行特性，使得高分子聚合物轴承在运行过程中通常会产生显著的弹性变形。因此，针对水润滑高分子聚合物尾轴承的工况特点，有必要将计入弹性变形的仿真方法引入轴承仿真模型中，建立适合于舰船水润滑尾轴承润滑特性计算的数值分析方法。

一般来讲，表面弹性变形量与最小液膜厚度处于同一数量级的润滑问题都属于弹性流体动压润滑(EHL)问题[1-2]。随着计算机技术及多场耦合计算的发展，流固耦合方法(Fluid-Structure Interaction，FSI)已经成为轴承弹流润滑分析的一种有力工具。LIU等[3]采用CFD-FSI方法研究轴承的弹性变形与动不平衡载荷对轴心轨迹的影响，将计算结果与基于雷诺方程的计算结果进行了对比，发现CFD-FSI方法的计算结果与试验结果更为接近。LIN等[4]利用CFD-FSI方法研究了不同的水槽分布对高速径向滑动轴承润滑性能的影响，研究表明水膜温度与空化体积分数随着转速的增大而增大，温升与空化体积分数随着沟槽数的增大而减小。LI等[5]利用CFD-FSI方法结合Fluent动网格技术研究了径向滑动轴承的瞬态流体动力学特性，并通过求解给定负载下轴承转子系统的运行方程分析了每一时间步下的轴心轨迹。SHENOY等[6]利用CFD-FSI方法研究了圆瓦轴承在不同长径比下的压力分布，并对轴承的应力与变形进行了评价，发现弹流润滑的计算结果与标准计算程序的结果有着较好的一致性。WANG等[7-8]基于CFD-FSI方法提出了考虑材料弹性变形及磨损劣化影响的水润滑高分子复合材料轴承仿真分析及优化设计方法，该方法提高了水润滑轴承的设计精度。BRUYERE等[9]提出了将N-S方程与弹性变形方程耦合求解弹流润滑的FSI计算方法，并用该方法计算了圆柱与平面相对滑动的算例，结果表明中心接触区域的摩擦热通过固体传导会造成入口区流体的温升。HONG等[10]在研究中提出，首先利用多重网格技术来确定初始膜厚，再采用改进的FSI计算方法能够更快速地获取计算结果。李正[11]、段海涛[12]、卢磊[13]、廖静[14]、戴明城[15]均采用流固耦合方法对水润滑PTFE及橡胶轴承的性能进行了系列研究。

然而目前针对弹性瓦轴承的试验研究还十分欠缺，尤其是针对UHMWPE基复合材料水润滑轴承的研究还不足。因此，开展UHMWPE基水润滑轴承偏心率测试、水膜厚度测试等是对当前数值研究的重要补充。本文作者首先分析了水润滑轴承的相关润滑理论，研究了水润滑尾轴承数值计算过程中的边界条件和润滑介质的流动状态，建立了计入弹性变形的轴承润滑性能分析方法，通过试验验证了计算方法的合理性，并且在此基础上计算了水润滑轴承的润滑性能，研究结果对水润滑聚合物复合材料尾轴承的设计提供有益支撑。

1 水润滑轴承数值分析方法

首先对流体微元的受力情况进行分析，建立流体微元的质量守恒方程、动量守恒方程和能量守恒方程。文中的数值求解是建立在连续性方程及Navier-Stokes方程的基础之上，求解过程中忽略水温变化对润滑状态的影响，因此不须求解能量方程。

取流体空间的一个单元，则在单位时间内流出的质量等于空间内质量的变化，即遵循质量守恒方程：

(1)

式中：ρ为流体密度；vx、vy、vz分别为速度矢量在x、y、z3个方向的分量。

流体质点动量守恒方程可表达为

(2)

式中：σi、τij(i，j=x，y，z)分别为作用在微元表面上的应力分量。

为准确计算轴承润滑性能，应选用合适的水膜破裂及再生成边界条件。随着计算流体力学软件的发展和进步，学者们提出了空化模型，ANSYS CFX采用基于Rayleigh-Plesset方程的空化模型，气-液之间的质量传递由公式(3)定义。

(3)

式中：Rb为气泡半径；pg为气泡内压力；σ为气液两相之间的表面张力系数。

在流体与固体的交界面上，流体压力使固体变形，反之固体变形也会改变流体的边界形状。流体与固体交界面上的单元遵循位移、应力、热流量、温度等变量相等的原则。文中忽略了计算中水介质温度的变化，故热流量与温度的变化不计。因此，有下列平衡方程：

(4)

式中：df、ds分别为流体位移、固体位移;τf、τs分别为流体质点与固体单元的应力。

水膜的边界条件设置如图1(a)所示，水膜左右两端面分别为压力入口及压力出口，水膜外表面与轴承接触，为流固耦合面，水膜内表面与轴接触，为旋转壁面。轴承固体域模型如图1(b)所示，轴承的内表面与流体域接触，设置为流固耦合面(Fluid solid interface)，轴承外表面为固定支撑面(Fixed support)。

图1 边界条件

2 水润滑轴承特性分析及验证

首先通过试验方法测试水润滑轴承的偏心率，并将测试结果与流固耦合数值计算结果对比。偏心率测试的相关试验研究采用课题组研发的高精度水润滑轴承试验机。试验轴材料为42CrMo，表面镀镍处理，轴的直径为80 mm，表面粗糙度Ra=0.2 μm。试验轴瓦材料为玻璃纤维(GF)和碳纤维(CF)复合填料改性的超高分子量聚乙烯(UHMWPE)复合材料，轴瓦内表面直径为80.12 mm，表面粗糙度Ra=2.0 μm。试验转速范围为1 500～2 000 r/min(线速度6.25～8.4 m/s)，试验负载为0.05～0.5 MPa。润滑介质为自来水，试验过程中轴承浸没在水箱中。试验机结构简图如图2所示。水润滑轴承试验机可以测量轴承的摩擦因数、水膜厚度以及水膜压力等参数。扭矩传感器、电涡流位移传感器的安装示意图如图3所示。为了方便对比，轴承试验与数值分析采用相同工况。

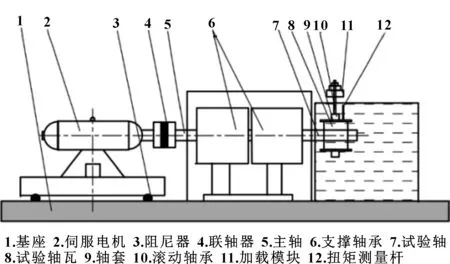
图2 水润滑轴承试验平台结构示意

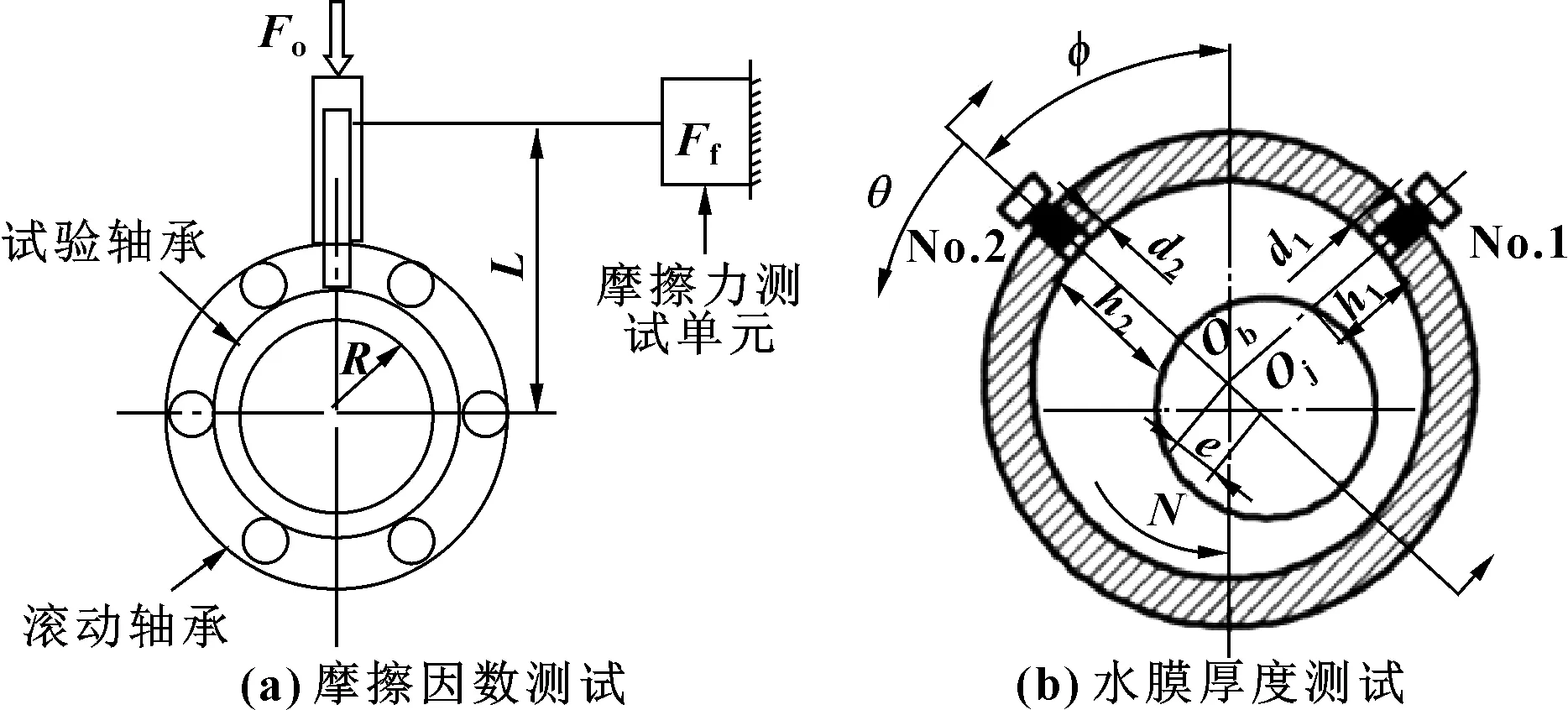
图3 水润滑轴承试验平台传感器安装示意

图4和图5分别示出了转速1 500和2 000 r/min时，UHMWPE复合材料轴承偏心率的试验值与计入弹性变形、不计入弹性变形的仿真值。研究表明，计入弹性变形和不计入弹性变形的计算结果与试验结果的变化趋势均一致，但计入弹性变形的结果与试验值更接近，表明文中流固耦合的数值计算方法具有更高的精度。试验结果表明，随负载增大，偏心率的仿真值与试验值之间一致性良好，计入弹性变形的偏心率与试验值之间的最大误差不超过15%。因此，由图4和图5可知，在不同转速及负载工况下，偏心率的仿真值与试验值一致性较好，试验结果能够验证文中水润滑轴承流固耦合数值计算方法的正确性。

图4 1 500 r/min时负载对偏心率的影响

图5 2 000 r/min时负载对偏心率的影响

此外，数值计算结果与试验值之间有一定误差，主要是因为：轴承的半径间隙值很小，试验轴的安装误差以及转轴运行过程中的径向跳动对测试结果有较大影响；试验加载方式为电机带动加力杆加载，试验过程中载荷波动对试验结果有一定影响；UHMWPE高分子材料的加工性能较差，在实际加工过程中很难获得高质量的轴承表面，这对试验结果也有一定影响。

3 结果与讨论

3.1 轴瓦材料弹性模量对润滑性能的影响

轴瓦材料的弹性模量随复合材料基体、配方、成型工艺的变化而变化。轴瓦材料弹性模量对轴承的承载能力和振动特性有重要影响，降低材料的弹性模量有利于提高轴承的减振及隔振性能，但会显著降低轴承的承载能力和耐磨性；反之，增加材料的弹性模量有利于轴承的承载能力和耐磨性的提高，但对轴承的减振和隔振性能不利。为了揭示材料弹性模量对水润滑尾轴承润滑特性的影响机制，从而获得最优的材料性能，有必要开展弹性模量对水润滑尾轴承润滑性能影响的相关研究工作。

计算时取高分子材料通用弹性模量范围400～2 000 MPa，泊松比为0.44；载荷及转速取尾轴承常用工况，载荷为0.24 MPa，转速为1 200 r/min(5 m/s)，轴承直径为80 mm，长径比为1.0，间隙比0.1%。图6示出了弹性模量对UHMWPE水润滑尾轴承偏心率、最小水膜厚度、最大水膜压力以及摩擦因数的影响。

研究表明，在相同载荷及转速工况下，随弹性模量增加，轴承运行的偏心率先逐渐减小后趋于稳定，表明轴承承载力随材料弹性模量的增大而增大，且弹性模量的大小对轴承偏心率的影响逐渐减小，如图6(a)所示。从图6(b)可看出，随着弹性模量的增大，最大水膜压力从0.46 MPa增大至0.52 MPa；在弹性模量较小时，最大水膜压力随弹性模量的增大迅速增大，但随着弹性模量的增加其对最大压力的影响逐渐减小。从图6(c)可看出，在弹性模量值较低时轴承变形量大，随着弹性模量的增大轴承变形量反而减小。从图6(d)可看出，随着弹性模量的增大，最小水膜厚度减小，轴承承载力随着弹性模量的增大而增大，因此轴承材料的弹性模量值应该在满足承载力的情况下，尽量取较小的值，以保证水膜厚度。

图6 弹性模量对轴承润滑性能的影响

3.2 轴瓦材料泊松比对润滑性能的影响

当轴承材料基体、制备方法、改性方法不同时，材料的泊松比有较大差异，因此有必要研究不同泊松比对水润滑轴承润滑特性的影响。计算时取泊松比范围为0.36～0.46，弹性模量为1 000 MPa，载荷为恒定值0.24 MPa，转速为1 200 r/min(5 m/s)，轴承直径为80 mm，长径比为1.0，间隙比0.1%。计算结果如图7所示。

从图7(a)可看出，随轴承材料泊松比的增大，轴承的偏心率逐渐减小，并且偏心率与泊松比基本呈线性关系，表明轴承承载力随轴承材料泊松比的增大基本呈线性增大。从图7(d)可看出，最小水膜厚度随泊松比的增大逐渐减小，两者之间基本为线性关系。上述结果表明，泊松比增大有利于增大轴承承载力，但是会造成轴承最小水膜厚度的减小，因此轴承材料的泊松比应在满足承载力要求的情况下，尽量选择较小的值，以避免水膜厚度过小造成轴承磨损。从图7(b)、(c)、(e)可看出：最大水膜压力随泊松比的增大基本不变；轴承最大变形随泊松比的增大逐渐减小；轴承摩擦因数随泊松比的增大也逐渐增大，但变化幅度较小。

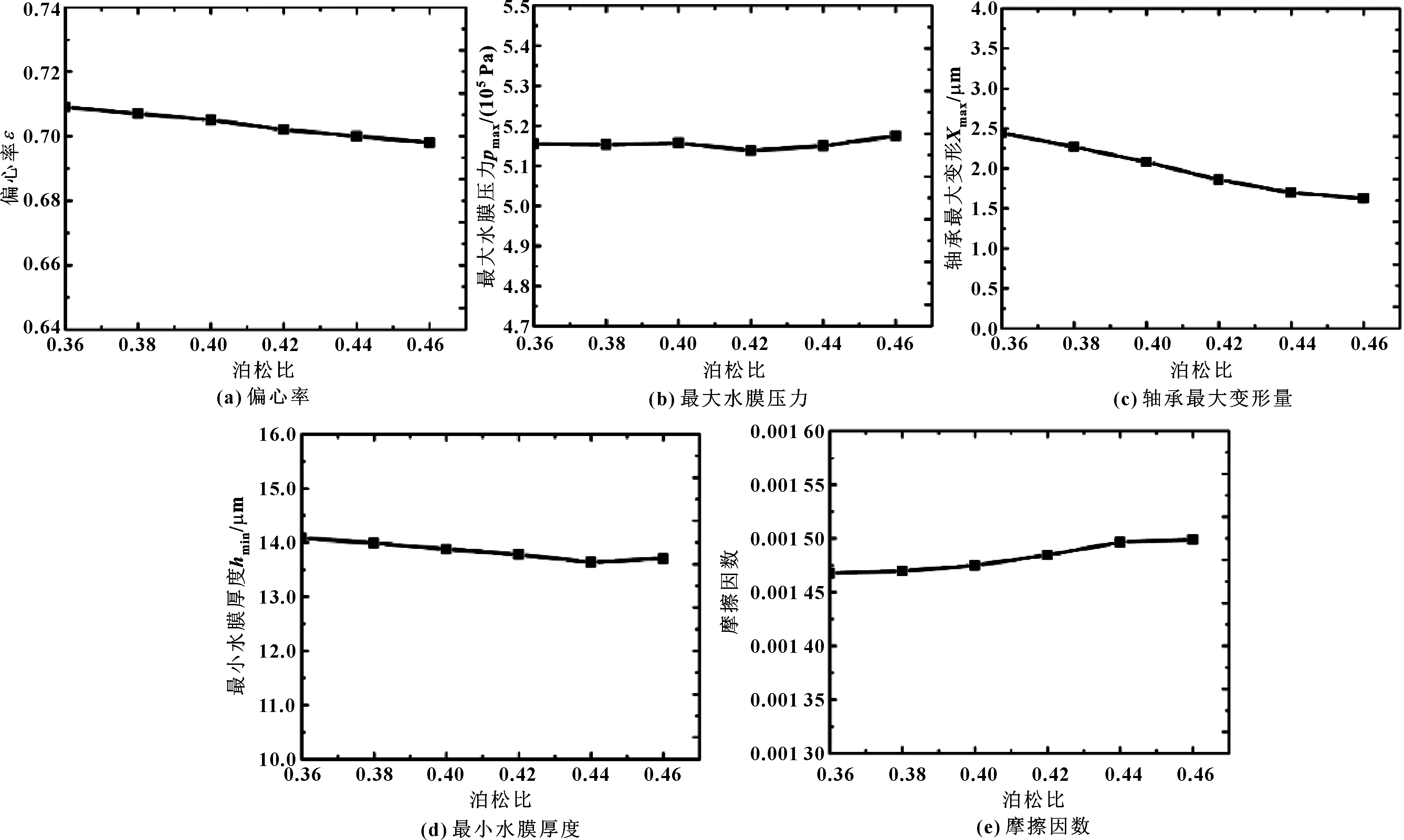
图7 泊松比对轴承润滑性能的影响

3.3 负载对轴承润滑性能的影响

轴承负载大小直接影响转轴相对于轴承的偏心距离，从而影响轴承润滑特性，因而有必要研究不同负载下轴承的润滑特性。尾轴承运行负载范围一般为0.1～0.3 MPa，极端恶劣工况局部负载可达到0.5 MPa甚至更大，因此计算时负载取值范围为0.1～0.75 MPa。其他计算参数为：转速1 200 r/min(5 m/s)，轴承直径80 mm，长径比1.0，间隙比0.1%，轴承材料弹性模量1 000 MPa，泊松比0.44。分别计算弹性轴承与刚性轴承的润滑特性参数，结果如图8所示。

从图8(a)可看出，在恒定转速工况下，当载荷从0.1 MPa增大至0.75 MPa时，轴承偏心率从0.4增大至0.95，并且偏心率的增大趋势逐渐趋于平缓，表明载荷越大对轴承承载力的影响越大。从图8(b)、(e)可看出，负载从0.1 MPa增大至0.75 MPa，轴承最大水膜压力从0.13 MPa增大至1.82 MPa，轴承最大变形量从0.4 μm增大至6.18 μm，并且两者与载荷之间基本呈线性增长关系。从图8(c)、(d)可看出，最小水膜厚度与摩擦因数均随载荷增大而减小，并且均在载荷较小时变化明显，而在载荷较大时，最小水膜厚度与摩擦因数的变化趋于平缓。

从图8(a)、(b)、(c)可看出，随着载荷的增大，弹性轴承与刚性轴承的偏心率、最大水膜压力、最小水膜厚度之间的差值逐渐增大；当负载为0.1 MPa时差值基本为0，当负载增大至0.7 MPa时偏心率、最大水膜压力、最小水膜厚度之间的差值分别为7%、38%、70%。这表明在重载工况下弹性变形对轴承润滑性能影响很大，UHMWPE水润滑尾轴承按照刚性轴承计算的结果与工程实际偏差较大，不再适用。因此，对于低速重载工况下运行的尾轴承，在数值计算中更应当计入弹性变形的影响。

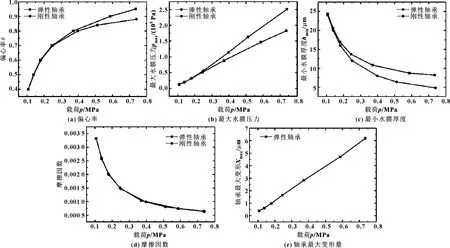
图8 不同载荷对轴承润滑性能的影响

3.4 速度对轴承润滑性能的影响

轴的转速大小直接影响滑动轴承动压润滑的形成状况，轴转动速度过低不足以形成动压润滑时，将造成轴与轴承表面微凸体接触，从而引发轴承材料的磨损失效。因此有必要分析转速对水润滑轴承动压润滑特性的影响，尤其是针对低速运行工况的尾轴承。

尾轴承的运转线速度一般不高于5 m/s，对应直径80 mm的轴承，其转速为1 200 r/min，因此计算时转速取值范围为400～1 200 r/min。其他计算参数为：载荷0.24 MPa，轴承直径80 mm，长径比1.0，间隙比0.1%，轴承材料弹性模量1 000 MPa，泊松比0.44。分别计算不同转速工况下，弹性水润滑轴承与刚性水润滑轴承的润滑特性参数，结果如图9所示。

从图9(a)可看出，在恒定载荷工况下，当转速从400 r/min增大至1 200 r/min时，轴承偏心率从0.9减小至0.7，并且变化基本呈线性关系，表明恒定负载下，轴承承载力随速度增大而线性增大。从图9(b)、(e)可看出，随转速增大，轴承最大水膜压力和轴承最大变形量显著减小。从图9(c)、(d)可看出，轴承最小水膜厚度与摩擦因数均随转速增大而增大。

从图9(a)、(b)、(c)可看出，计入弹性变形后，轴承的偏心率、最大水膜压力以及最小水膜厚度均有较大改变，弹性轴承与刚性轴承相比，相同工况下的偏心率有所增大、最大水膜压力显著减小、最小水膜厚度显著增大；此外，在恒定载荷工况下，转速越低，轴承弹性变形对轴承承载力、最大水膜压力和最小水膜厚度的影响越大。