主跨1 216 m斜拉桥试设计及静动力性能分析
2021-02-27邓卓章
邓 卓 章
(同济大学土木工程学院桥梁工程系,上海 200092)
1 概述
斜拉桥是现代大跨度桥梁的重要结构形式,具有跨越能力强,造型美观等优点,并具有良好的力学性能和经济指标,施工技术也较为成熟,因此在交通领域得到了广泛应用[1]。2008年,主跨1 088 m的苏通长江大桥刷新了世界斜拉桥跨径记录。2020年,主跨1 092 m的沪通长江大桥刷新了我国斜拉桥跨径记录。主跨1 176 m的常泰长江大桥和主跨1 120 m的马鞍山长江公铁大桥正在建设中,建成后将再度刷新世界斜拉桥跨径记录。斜拉桥正在不断突破跨径记录,本文进行一座主跨1 216 m斜拉桥的方案试设计,探讨进一步突破斜拉桥跨径的可行性。
2 方案试设计
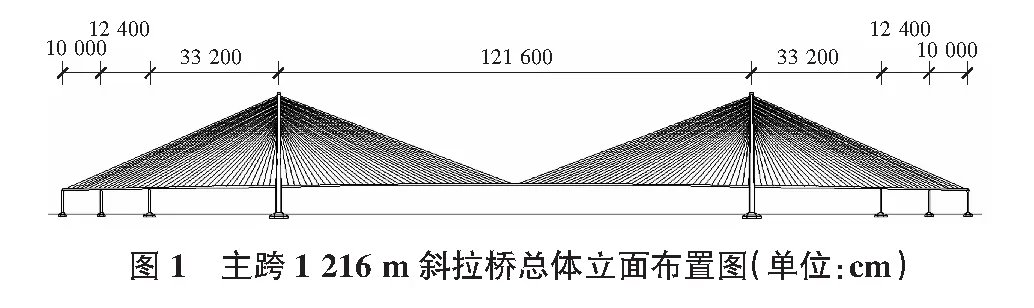
拟定的主跨1 216 m公路钢箱梁斜拉桥试设计方案的跨径布置为100 m+124 m+332 m+1 216 m+332 m+124 m+100 m,见图1。每个边跨设置两个辅助墩,边跨跨径为556 m,边中跨比为0.457。采用全漂浮体系,索塔与主梁之间仅设置横向抗风支座和纵向具有限位功能的粘滞阻尼器,不设竖向支座。
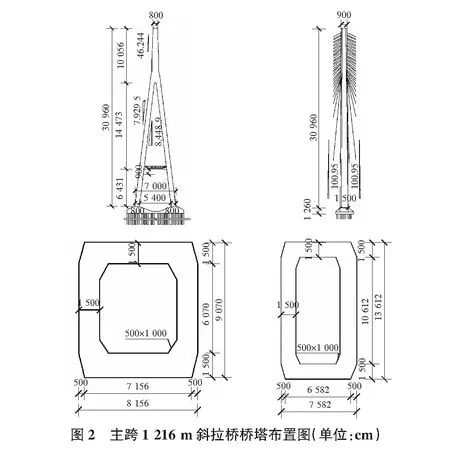
桥塔采用横桥向倒Y形、顺桥向直立单柱式混凝土塔柱,见图2。混凝土标号为C50。桥塔桥面以上高度239.61 m,高跨比为1/5.028。桥塔总高度为309.60 m,其中上塔柱100.56 m,中塔柱144.73 m,下塔柱64.31 m,塔底两肢塔柱中心间距62 m。塔柱采用空心箱形断面,上塔柱为对称单箱单室,尺寸由9.00 m×8.00 m变化到10.60 m×14.56 m,塔壁厚度为1.50 m,中间设钢锚箱。中、下塔柱为不对称的单箱单室断面,尺寸由10.82 m×6.50 m变化到15.00 m×8.00 m,中塔柱壁厚1.50 m,下塔柱壁厚1.80 m。为保证下塔柱能够抵抗船舶撞击力,下塔柱底部设10.00 m实心段。
主梁采用流线型扁平钢箱梁,见图3。钢材牌号为Q390。主梁梁高4.00 m,高跨比为1/304,主梁全宽41.0 m,两侧各设置约2.80 m宽的风嘴。主梁每隔4 m设置一道横隔板,顶板在顺桥向不同区段采用18 mm~28 mm的厚度,腹板厚度为32 mm~38 mm,底板厚度为16 mm~28 mm。

斜拉索布置为扇形倾斜双索面密索体系,采用抗拉强度为1 860 MPa的平行钢丝拉索,全桥共计4×38×2=304根拉索,规格为PES7-139~PES7-451。单索最长为639.27 m,单索最大重量为86.39 t。斜拉索在主梁上锚固点间距为16 m,边跨尾索区为12 m,在桥塔上锚固点的平均间距为2.45 m。
3 有限元计算模型
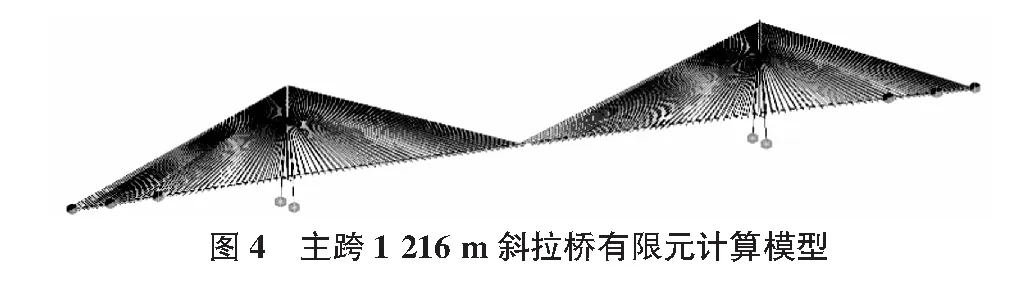
采用MIDAS/Civil建立三维鱼骨梁全桥有限元计算模型,主梁和主塔采用梁单元模拟,斜拉索采用只受拉索单元模拟。全桥共离散为1 450个节点、1 124个单元(其中梁单元820个,只受拉索单元304个),有限元计算模型见图4。
4 结构静力性能分析
4.1 施工阶段计算分析
根据施工方案将施工流程划分为179个施工阶段,斜拉索的一张力和二张力采用综合考虑施工过程和合理成桥状态的原则进行确定。
施工过程中主梁的最大竖向变形发生在拆除中跨吊机时,其主跨跨中向上挠度为2.303 m,施加二期恒载后,主跨跨中向上挠度为0.014 m。主塔塔顶的最大偏位同样发生在拆除中跨吊机时,向岸侧偏位53.31 cm,施加二期恒载后,塔顶向岸侧偏位9.25 cm。
施工过程中主梁的最大正应力-98.86 MPa,在边跨A06号索位置。主塔的最大压应力为11.84 MPa,在中塔柱底部。斜拉索的最大应力为726 MPa,为12号梁段吊装时的索J11。
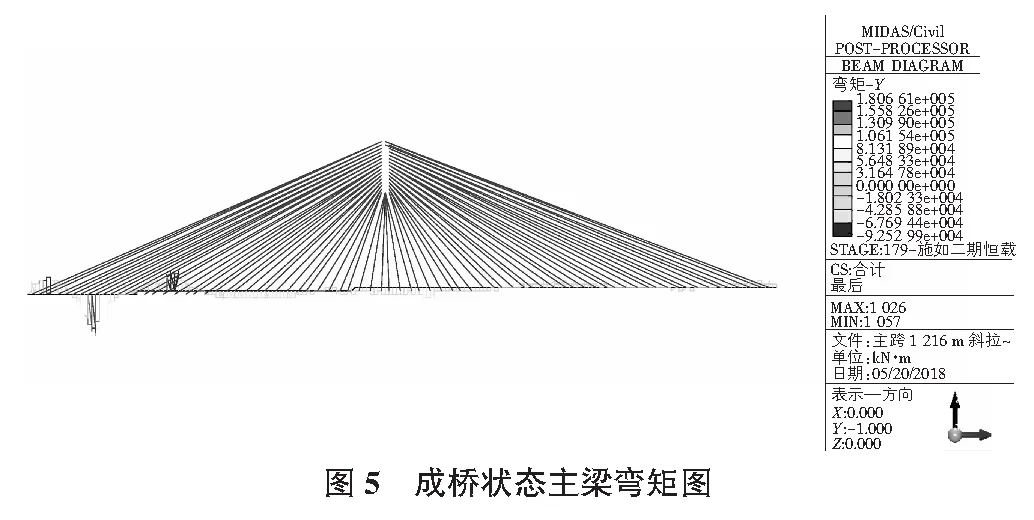
成桥状态主梁弯矩见图5,除了辅助墩跨之外,其余部分主梁弯矩均较小,满足合理成桥状态要求。
4.2 运营阶段计算分析
运营阶段考虑了汽车荷载、风荷载、温度荷载、基础变位作用,按照规范进行作用效应组合,主梁、主塔和斜拉索在最不利基本组合下的应力包络图见图6~图8。
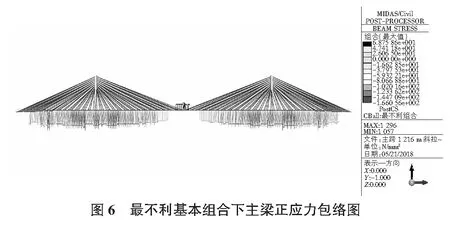
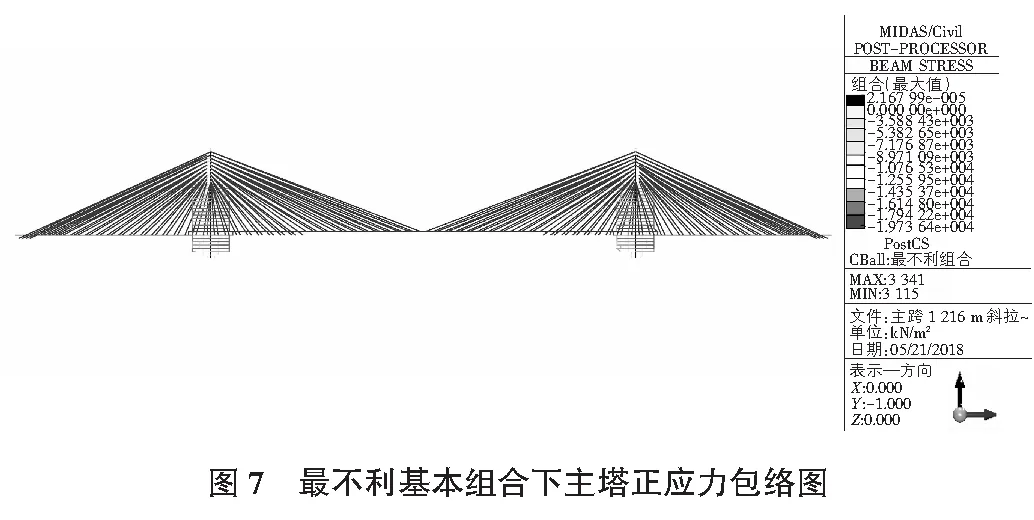
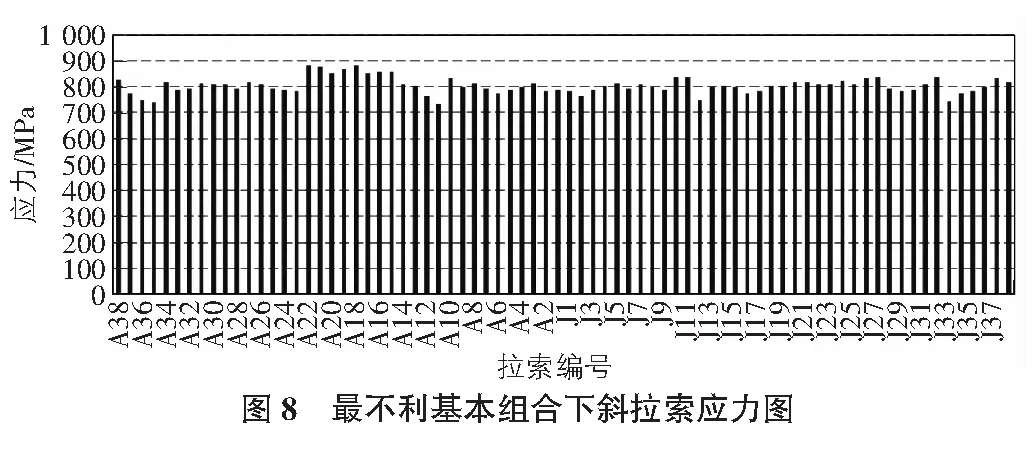
主梁在最不利基本组合下的最大正应力-166.06 MPa,主塔最不利基本组合下的最大压应力为19.74 MPa,斜拉索在最不利基本组合下的最大应力为882.92 MPa,均满足强度要求。主梁在汽车活载作用下的最大正挠度为1.707 m,满足刚度要求。
4.3 静力稳定性分析
对最大双悬臂状态、最大单悬臂状态、成桥恒载状态和全桥满布活载状态进行弹性屈曲稳定分析,结果见表1。结构在恒载+全桥满布活载时一阶失稳系数最小,为4.02,但仍满足静力稳定性要求。

表1 静力稳定性分析结果
4.4 活载几何非线性效应分析
大跨度斜拉桥结构分析必须计入几何非线性的影响,相应地,对于活载效应分析也涉及几何非线性因素的考虑[2]。一般在常规分析中,仅考虑了成桥状态恒载的初始几何刚度,仍然按照线性方法求解影响线并根据线性叠加原理计算活载效应。为了研究这种仅考虑恒载初始几何刚度的方法在活载几何非线性效应方面的误差,选取了4个有代表性的控制工况,将对应的活载布置导出作为静力荷载作用在结构上进行几何非线性计算,将两种方法的计算结果进行对比,对比结果见表2。
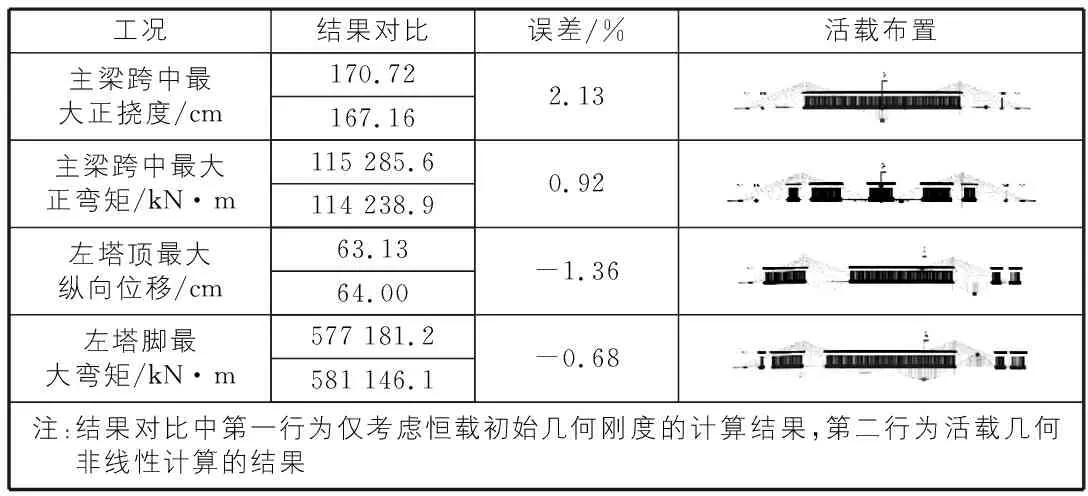
表2 活载几何非线性效应分析结果
从表2结果可以看出,仅考虑恒载初始几何刚度的计算结果与活载几何非线性计算的结果误差均在3%以内,其中主梁跨中最大正挠度的误差最大为2.13%。这说明即使对于千米级斜拉桥,虽然其几何非线性效应突出,但是由于活载占比很小,对于活载采用仅考虑恒载初始几何刚度的方法仍然是可行的。
5 结构动力性能分析
大跨度桥梁结构的动力特性如固有频率、振型等,是评价结构整体性能的重要依据之一,是进行结构抗风、抗震等动力学问题研究的基础[3]。采用Lanczos法对该桥进行了动力特性分析,考虑成桥状态恒载的初始几何刚度。动力特性分析结果见表3。
根据动力特性分析得到的一阶正对称竖弯频率和一阶正对称扭转频率就可以估算颤振临界风速,采用半逆解法[4],先根据理想平板导数得到平板颤振临界风速为150.35 m/s,再根据规范上的形状系数和攻角效应系数得到桥梁颤振临界风速为84.20 m/s,大于颤振检验风速52.65 m/s,故颤振稳定性满足要求。
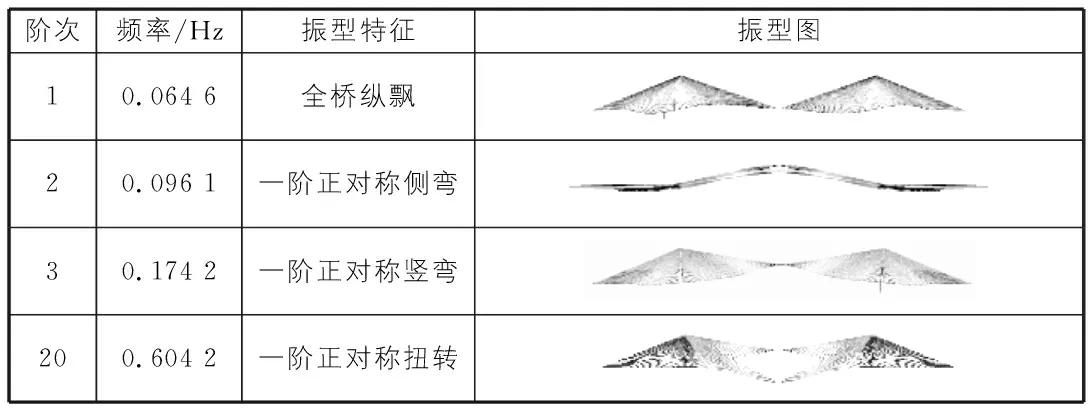
表3 动力特性分析结果
6 结语
经过有限元模型的静动力性能分析验证,主跨1 216 m斜拉桥试设计方案在强度、刚度、静力稳定性、颤振稳定性方面均满足设计要求,故该方案是可行的。通过分析和研究,可以为超大跨度斜拉桥的设计提供参考。
