一种决策形式背景中挖掘决策规则的新方法

毛华，郑珍，刘晓庆

(河北大学 数学与信息科学学院，河北 保定 071002)

概念格1982年由Wille[1]首次提出，作为一种知识发现和数据分析的有效工具，已在数据挖掘、机器学习、知识发现、软件工程和信息获取等领域中有着广泛的应用[2-7].

在概念格研究领域中，利用频繁项集进行关联规则的提取和频繁模式的发现是至关重要的.将频繁闭项集用于概念格挖掘关联规则，可使规则数量大大减少，但同样能够得出与全部规则集相同的决策.Rakesh[8]提出了著名的Apriori先验算法用来挖掘频繁项集，并生成关联规则；付沙等[9]改进了关联规则挖掘Apriori算法，基于构造辅助表和项集求交集策略，改进算法显著提高了频繁项集的生成效率，从而使算法达到更高的运算效率；Hafida等[10]定义语义模式，通过频繁概念格进行查找与语义模式相关联的服务集合.在一些实际应用中，基于频繁闭项集在概念格中提取关联规则的研究也有不少成果[10-16].

目前，有关决策规则的挖掘仍然是决策形式背景中研究的重要内容[17-23]，但有些决策规则提取方法并没有给出可操作的算法过程[19,22-23]，甚至已有的一些算法不能适用于大规模决策形式背景的决策规则提取[20]，即如何在大规模决策形式背景中挖掘决策规则的问题目前还没有得到很好的解决.

由于频繁闭项集可用来压缩数据集规模，过滤掉大量的冗余决策规则，故而可以考虑将频繁闭项集与决策形式背景相联系，提取具有较高可信度的决策规则集，并给出可实现的算法过程，利用此决策规则集快速、精准地做出决策.

1 预备知识

定义1[24]假设给定形式背景(U,A,I)为三元组，其中U是对象集合，A是属性集合，I是U和A之间的一个二元关系，I⊆U×A，若(x，a)∈I,则称x具有属性a，记为xIa.

对于形式背景(U,A,I)，在对象集X⊆U和属性B⊆A上分别定义运算：X′={a|a∈A,∀x∈X,xIa},B′={x|x∈U,∀a∈B,xIa}.

定义2[25]1)设I={i1,i2,…，in}s是n个不同项目的集合，如果对于一个集合X，有k=|X|，X⊆I，则称X为k项集.设D为事物T的集合，T⊆Ω，对于给定的事物数据库D，定义X的支持度为D中包含X的事物个数，记为sup(X)，用户自定义一个小于|D|的最小支持度，记为α.

2) 给定事物数据库D和α，对于项集X⊆I，若sup(X)≥α,则称X为D中的频繁项集.

3) 设项目集X⊆I，如果满足Y″=Y，则称X为闭项集.如果X同时是频繁项集，则称X为最大频繁闭项集，简称频繁闭项集,记为FCI.频繁闭项集中所包含的项目的数目|X|称为闭项集的长度.

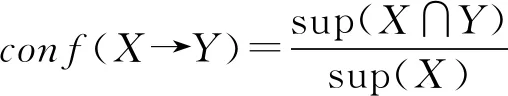
引理1[13]设(U,A,I)为一个形式背景，称(A,B)为这个形式背景的一个概念，则概念(A,B)对应的内涵是频繁闭项集当且仅当内涵B是频繁项集，此时称(A,B)为频繁概念.

2 无冗余决策规则提取

基于概念格的频繁闭项集提取算法[13]在概念格中遍历了全部概念，提取频繁闭项集.本文算法1中利用概念节点间的父子关系，无需遍历全部概念节点，改进频繁闭项集在概念格中的挖掘算法，算法思路如下：

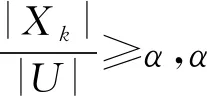
算法过程如下.

算法1频繁闭项集挖掘的改进算法

输入：概念格L1(U,A,I)，最小支持度α；输出：频繁闭项集FCI.

步骤1 inti=0,FCI=φ，rooti=(Xi,Yi)

步骤2 fori=1 ton{Red-lattice(rooti)

ifrooti≠ΦRed-lattice(rootj)

else

end if

else

end if}

end for}

步骤3 PrintfFCI

定理1对于2个概念C1=(A1,B1)和C2=(A2,B2)，且C2是C1的父节点，若|A1|≥min sup，则必有|A2|≥min sup.

证明：由于C2是C1的父节点，必有A1⊆A2，则|A1|≤|A2|，故|A1|≥min sup，证毕.

定理2算法1中当循环i=n+1时，算法程序结束.当算法1结束时，输出的FCI必为频繁闭项集.

证明：当i=n+1时，根节点rooti=Φ，循环终止，算法程序结束；又由引理1可知，每一个概念的内涵必为一个频繁项集，故保留下来的每个概念都是频繁的，从而证明FCI必为频繁闭项集，证毕.

由定理1可知，若父概念不是一个频繁概念，那么它的子概念必定不是频繁概念.由定理2可知，算法1在概念格中得到频繁闭项集，进而说明了算法1的正确性.另外，算法1过滤掉了部分概念，这也在一定程度上压缩了决策规则集.

定义3对于Y∈FCI,Y′=X,(B,C)∈L(U,D,J),若X∩B≠Φ,则可将概念扩充为(X∩B,Y,C),称之为频繁决策概念，其中X∩B称为频繁决策概念外延，Y称为频繁决策概念内涵，C称为频繁决策集.

定义41) 从频繁决策概念中可直接得到决策规则为Y→C，表明由条件属性Y可做出决策C，若E⊂Y且E→C成立，则称决策规则Y→C是冗余的.

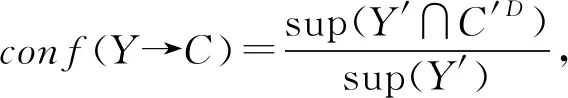
决策形式背景中决策规则提取的算法思路如下：利用算法1中得到的全部频繁闭项集FCI，对每一个频繁闭项集Y计算其概念外延Y′=X，用渐进式算法[26-27]建立概念格L2(U,D,J)={(Bj,Cj)|j=1,2,…，m},对每一个(Bj,Cj)中的外延判断是否满足条件X∩Bj≠Φ,若满足，则可得到频繁闭项集对应的频繁决策概念(X∩Bj,Y,C).提取决策规则Y→C,并由定义4判断其是否冗余，进而得到无冗余的决策规则集，计算出规则置信度.

具体实现过程如下.

算法2决策形式背景中决策规则的提取

输入:频繁闭项集FCI={Yi|i=1,2,…,n}，L2(U,D,J)；输出:无冗余决策规则R和置信度conf.

步骤1 inti=1,Mt=Φ,R=Φ

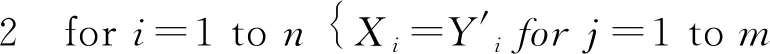
{ifXi∩Bj≠Φ thenMi=(Xi∩Bj,Yi,Cj)R=R∪(Yi→Cj)

else

end if}

end for}

end for

ifE→CjandE⊂Yithen

R=R-(E→Cj)

else

end if

end

步骤3 Printf(Randconf(Yi→Cj)

算法2中当内循环j>m时，说明L2(U,D,J)中的概念已经全部遍历完，内循环结束.外循环i>n时说明已找到全部的频繁闭项集的外延，外循环结束，所以算法2必在经过第n×m次循环后结束.

定理3决策规则集R数量上大大减少，且一定是无冗余的决策规则集.

证明：显然，由定义3和定义4可直接证明.

由定理3可知，算法2结束可得到数量少且无冗余的决策规则集，进而说明了算法2的正确性.

下面将分别对本文中给出的算法1和算法2进行复杂度分析，并通过与已有的产生频繁项集以及提取决策规则的相关著名算法和方法进行比较，分析得出本算法的优势.

算法1在概念格的基础上，更新概念节点后每个概念的内涵便是频繁闭项集，针对每一个节点内涵(即频繁闭项集)进行搜索，故算法1中最坏的情况下的时间复杂度为O(|FCI|).

与已有算法相比较，分析得出算法1优势如下：

1)Aprior算法[9]是产生频繁闭项集提取关联规则的著名算法，主要有以下缺点：一方面，算法中需要生成的候选项集数目庞大，呈指数级增长，例如一家超市有一千种商品，则就会有21 000-1 个候选项集；另一方面，每个候选项集都要和每个事务相比较，事务数量越大，计算次数就会越多，且再由其产生关联规则的时间复杂度为O(|FCI|2)，其中|FCI|是频繁闭项集的数目.显然本文算法1中基于概念格的节点关系得到频繁项集大大节省了寻找频繁闭项集的时间.

2)翟悦等[13]在概念格的基础上生成频繁闭项集的算法需要遍历概念格中全部的概念节点，而本文算法1中，利用了概念节点的特化与泛化关系，以及深度优先搜索的思想，无需遍历全部概念节点，降低了算法的复杂度.

算法2中通过频繁决策概念格提取全部决策规则的算法复杂度为O(m×n)(m、n分别为频繁决策概念和频繁闭项集的个数)，生成无冗余决策规则的算法复杂度为O(r2)(r为全部决策规则数)，最终算法2的时间复杂度为O(m×n+r2).

与已有算法相比较、分析，得出算法2优势如下：1) 魏玲等[19,23]仅是从理论方面给出了决策规则的提取方法，并没有给出算法过程，无法直接实现.本文不仅给出了理论分析，还将理论通过可行的算法加以实现，因此，本文的思想和方法可操作性较强；2) 李金海等[18]在决策形式背景中给出了一个更为高效的算法用来挖掘无冗余的决策规则，但得到的是全部规则集，时间复杂度为O((|U|+|A|)|LA|+|D||LA|2)，对于具有一定规模的决策形式背景，随着对象个数和属性个数的不断增加，算法的复杂度相当高，而本文给出的算法的时间复杂度会略低于文献[18].

由以上分析看出，本文给出的2个算法与现有算法和方法相比，生成无冗余决策规则的算法复杂度较低，并且利用频繁决策概念格压缩了数据集规模，空间复杂度降低，更适用于具有一定规模的数据集的处理，因此本文算法要优于其他一些已有算法或方法.

3 实例验证

从UCI机器学习数据库中，随机选取ABALONE数据集的前50个对象进行实验，整理之后得到如表1所示的决策形式背景(U,A,I,D,J),其中对象集U={1,2,3,4,5,6,7,8,9,10}，条件属性集A={a1,a2,a3,a4,a5,a6,a7}，决策属性集D={d1,d2,d3}.

表1中，条件属性集分别代表鲍鱼的体态特征，a1代表长度，a2代表直径，a3代表高度，a4代表全重，a5代表去壳的重量，a6代表脏器的重量，a7代表环数.决策属性集分别代表鲍鱼的性别，d1代表雄性，d2代表雌性，d3代表幼儿.

在此决策形式背景中，条件属性集所对应的形式背景(U,A,I)共有12个概念，即(U,A,I)={(U,Φ),2 567 910,a1),(145 678 910,a7),(2 567,a1a2),(5 789,a3a7),(567 910,a1a7),(567,a1a2a6a7),579,a1a3a7),(57,a1a2a3a6a7),(7,a1a2a3a4a6a7),(Φ,A)}.决策属性所对应的形式背景(U,D,J)共有5个概念，即L(U,D,J)={(U,Φ),(110,a),(256 789,b),(34,c),(Φ,D)}.

首先执行算法1，计算决策规则置信度如下：

表1 决策形式背景

算法1寻找FCI的复杂度为O(|FCI|)=O(5),算法2提取全部的无冗余规则的复杂度为O(|m×n+r2|)=O(5×6+52)=O(55).因此，本例中的算法复杂度为O(|FCI)|+O(m×n+r2)=O(5)+O(55)=O(60).

图1 不同规模决策形式背景下2种算法的执行时间比较Fig.1 Comparison of execution time of two algorithms with different fornal decision content

为了验证算法的有效性，主要比较本文算法2与文献[18]中算法的性能差异.实验环境为:3.5 GHz CPU I5,16 G内存,Windows 10系统.算法采用Matlab语言编程，由于随机函数不仅可以灵活地产生所需数据集而且无需预处理，因此实验所需数据随机产生.图1是针对不同规模的决策形式背景，在相同的支持度下，分别采用本文算法与文献[18]中的算法挖掘决策规则，图1可看出，当对象集的数量n=10时，2种算法在时间上相差不大；当对象集的数量n=20、30时，本文算法在时间上略优于文献[18]中的算法，但差距不大，直到n=50时，本文算法在时间上大大优于文献[18]中的算法，即随着决策形式背景规模的增加，本文算法在执行时间上的优越性会越来越明显.因此，通过以上分析说明本文中给出的通过频繁决策概念格提取决策规则的方法效率较高，更适用于在具有一定规模的数据集中挖掘决策规则.

4 结论

本文提出了一种在决策形式背景中挖掘决策规则的新方法,改进了概念格中挖掘频繁闭项集的算法，给出了决策形式背景中挖掘无冗余决策规则的算法.利用频繁闭项集可删减掉大量冗余规则，进而得到频繁决策概念，从中挖掘带有置信度的无冗余决策规则.实例表明，本文给出的算法复杂度较低，执行效率较高，更适用于具有一定规模的决策形式背景中获取无冗余决策规则.下一步考虑将此思想应用到加权决策形式背景的知识获取上，可根据实际情况中决策形式背景中的条件属性和决策属性的重要程度不同，分别对其赋予带有某种意义的权值，以确保某些有意义的信息不被遗漏.