非均等排序集抽样下位置参数的Mann-Whitney检验

张良勇， 董晓芳

(河北经贸大学 数学与统计学学院，河北 石家庄 050061)

非均等排序集抽样(Ranked set sampling with unequal samples，简写为RSSU)方法用于提高抽样效率[1]，其抽样步骤为：第1步，在总体中随机抽出m2个个体，分成m组，第i组个体数为mi=2i-1，i=1,2,…,m；第2步，根据直观感知的信息对每一组进行由小到大的排序；第3步，在第i组抽出次序为i的个体，i=1,2,…,m。以上步骤为一次循环，为了增大样本量，进行k次循环，得到样本量为n=mk的非均等排序集样本，记为

X(i:2i-1)j，i=1,2,…,m；j=1,2,…,k

其中X(i:2i-1)j为第i组中第i次序统计量的第j次循环。RSSU样本单元之间独立，另外对于任取的i(i=1,2,…,m)，X(i:2i-1)1,X(i:2i-1)2,…,X(i:2i-1)k的分布均与样本量为2i-1的简单随机样本中位数的分布相同。

均等排序集抽样(Ranked set sampling with equal samples，简记为RSSE)过程的第1步是从总体中随机抽取大小为m2的简单样本，分为m组，每组m个单元。其余抽样过程与RSSU方法一样。可见RSSE包含各个次序的信息相等[2]，而RSSU集中包含了中位数的信息。文献[3-7]研究了基于RSSU方法的估计问题和检验问题，这些文献的研究结果均表明：RSSU方法的抽样效率高于RSSE方法和简单随机抽样(Simple random sampling，简称为SRS)方法。

针对两个未知总体位置参数的检验问题，文章提出基于RSSU方法的Mann-Whitney检验统计量，分析其统计性质，并进行检验功效的模拟比较。

1 基于RSSU方法的Mann-Whitney检验统计量

设未知总体X和Y的分布函数分别为F(x-θ1)和F(y-θ2)，其中F(t)连续。假设检验问题为

H0:θ1=θ2↔H1:θ1>θ2

(1)

此检验问题称为两位置参数的右单侧问题。H1也可为θ1<θ2和θ1≠θ2，分别对应左单侧和双侧检验。

令X(i:2i-1)j，i=1,2,…,m；j=1,2,…,k为X的RSSU样本，X(i:2i-1)j的概率密度函数与分布函数为

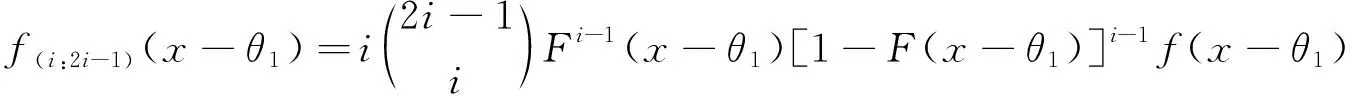
(2)

(3)

其中f(x-θ1)表示X的密度函数。令Y(r:2r-1)s，r=1,2,…,p；s=1,2,…,q为抽自Y的RSSU样本，Y(r:2r-1)s的密度函数和分布函数分别为f(r:2r-1)(y-θ2)和F(r:2r-1)(y-θ2)。

基于RSSU方法的Mann-Whitney检验统计量定义为

(4)

其中I(·)为示性函数。显然对于检验问题(1)，若URSSU过大，则有理由拒绝H0。

2 统计性质

根据公式(4)，检验统计量URSSU的数学期望为

(5)

当H0成立时，θ1=θ2。再由公式(2)、(3)和(5)，得

其中

(6)

定理1若总体分布F(t)连续且严格单调，则在H0下，URSSU具有与F(t)无关的对称分布。

证明当H0成立时，根据公式(4)和F(t)的严格单调连续性，得

(7)

其中U(i:2i-1)j，i=1,2,…,m，j=1,2,…,k和V(r:2r-1)s，r=1,2,…,p，s=1,2,…,q都是来自均匀分布U(0,1)的RSSU样本。于是，在H0下URSSU的分布与F(t)无关。

根据RSSU样本的分布性质，容易推得

再由公式(7)，得

证毕。

定理2如果当k+q→时，

那么当k+q→时，

其中

(8)

(9)

特别地，当H0成立时，

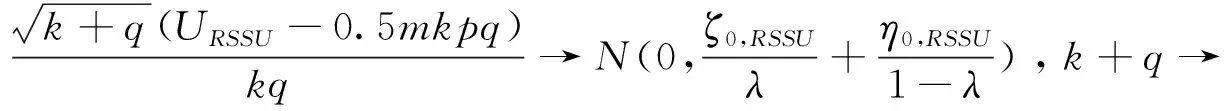
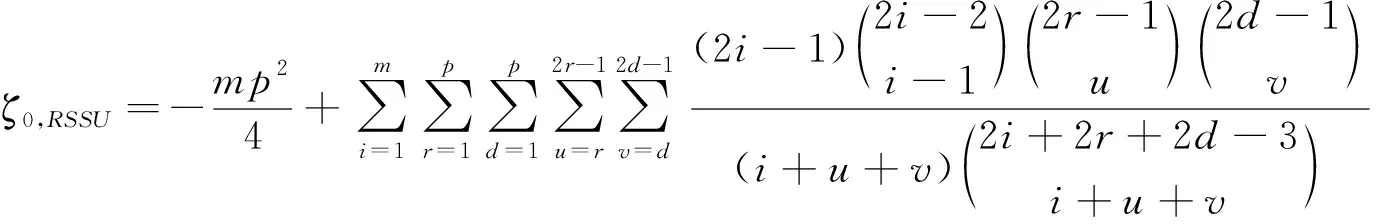
(10)

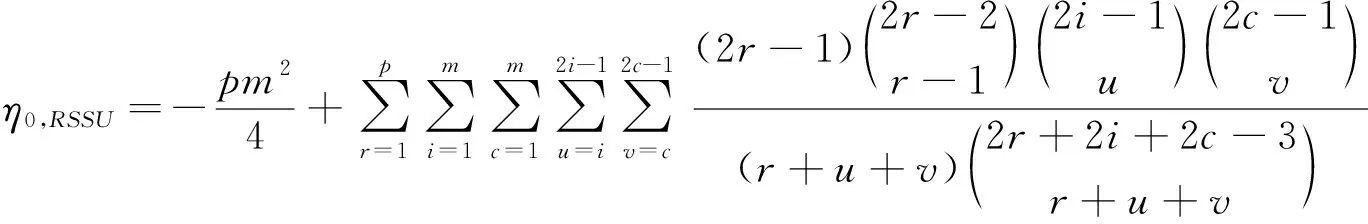
(11)

证明令

Xj=(X(1:1)j,X(2:3)j,…,X(m:2m-1)j)，j=1,2,…,k

Ys=(Y(1:1)s,Y(2:3)s,…,Y(p:2p-1)s)，s=1,2,…,q

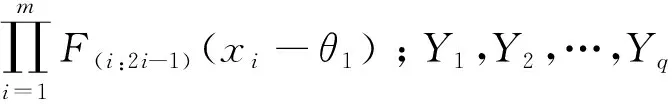
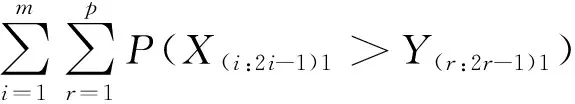
(12)

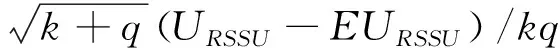
其中

ζRSSU=Cov[h(X1,Y1),h(X1,Y2)]=E[h(X1,Y1)h(X1,Y2)]-E2[h(X1,Y1)]

(13)

ηRSSU=Cov[h(X1,Y1),h(X2,Y1)]=E[h(X1,Y1)h(X2,Y1)]-E2[h(X1,Y1)]

(14)

由公式(12)，得

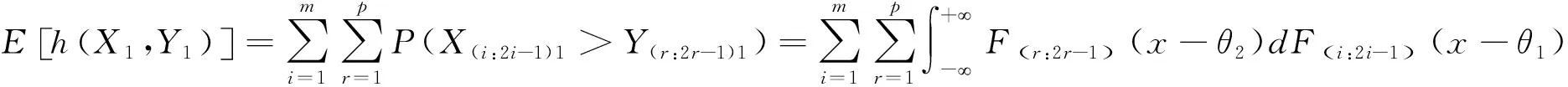
(15)

E[h(X1,Y1)h(X1,Y2)]

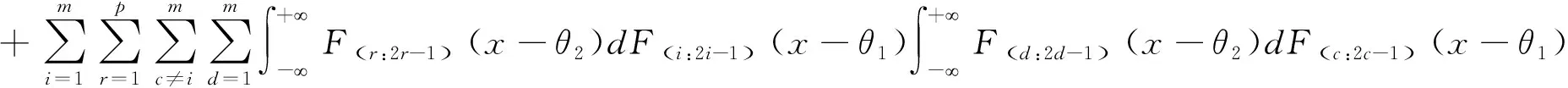
(16)

将公式(15)和(16)代入式(13)，整理后即得公式(8)，同理可得公式(9)。当H0成立时，θ1=θ2，再由公式(6)即得公式(10)和(11)。

证毕。

从定理2知，对于右单侧检验问题(1)和显著性水平α，若样本量较大，则当

时拒绝H0，其中u1-α为标准正态分布的1-α分位数。

3 模拟检验功效

令USRS表示基于简单随机样本的Mann-Whitney检验统计量[9]，URSSE表示基于均等排序集样本的Mann-Whitney检验统计量[10]，它们的样本量都与非均等排序集样本量相同，也都是针对右单侧检验问题(1)。

下面通过计算机来模拟计算统计量USRS、URSSE和URSSU的检验功效。总体分布F(t)选取为：正态分布N(0,1)、Logistic分布Log(0,1)、指数分布Exp(1)和对数正态分布LN(0,1)。取定F后，总体X和Y的位置参数选为：θ1-θ2=0,0.25σ,0.5σ,0.75σ,σ，θ2=0，其中σ2=Var(X)=Var(Y)。另外，显著性水平α取为0.05，(m,k,p,q)=(3,8,3,8)和(4,6,4,6)。

首先确定USRS、URSSE和URSSU的临界值。由文献[9-10]知，在H0下USRS和URSSE的分布都不依赖于F(t)。这样，检验临界值只需对一种分布进行模拟，我们选取F(t)为N(0,1)，模拟次数为50000次。表1给出了USRS、URSSE和URSSU的模拟临界值和犯第一类错误的概率。

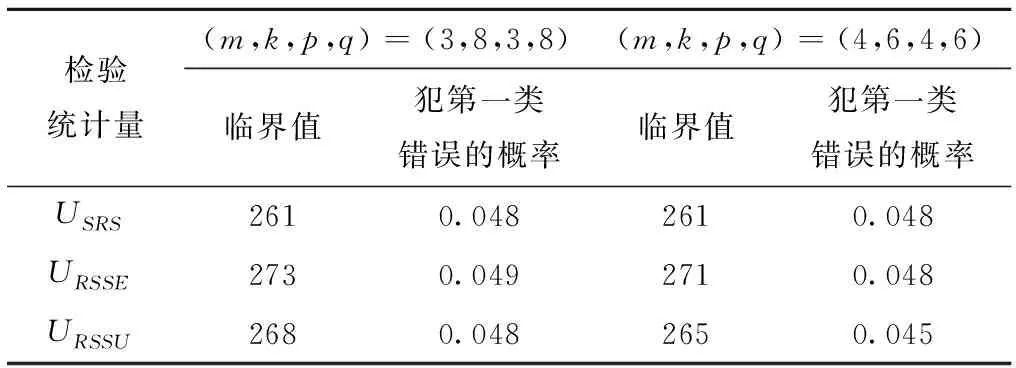
表1 Mann-Whitney检验的模拟临界值和犯第一类错误的概率

表2给出了USRS、URSSE和URSSU的模拟检验功效值，模拟次数为10000次。可以看出，对于给定的(F,θ1,θ2,m,k,p,q)，统计量URSSE的检验功效高于USRS，统计量URSSU的检验功效高于URSSE。

4 结论

文章采用RSSU方法，首先建立了两总体位置参数的Mann-Whitney检验统计量URSSU；其次计算了URSSU的数学期望，证明了当H0成立时URSSU具有不依赖总体的对称分布；然后证明了URSSU的渐近正态性，并计算出其渐近方差；最后计算出USRS、URSSE和URSSU的模拟检验功效，结果表明：RSSU方法的抽样效率高于SRS方法和RSSE方法。

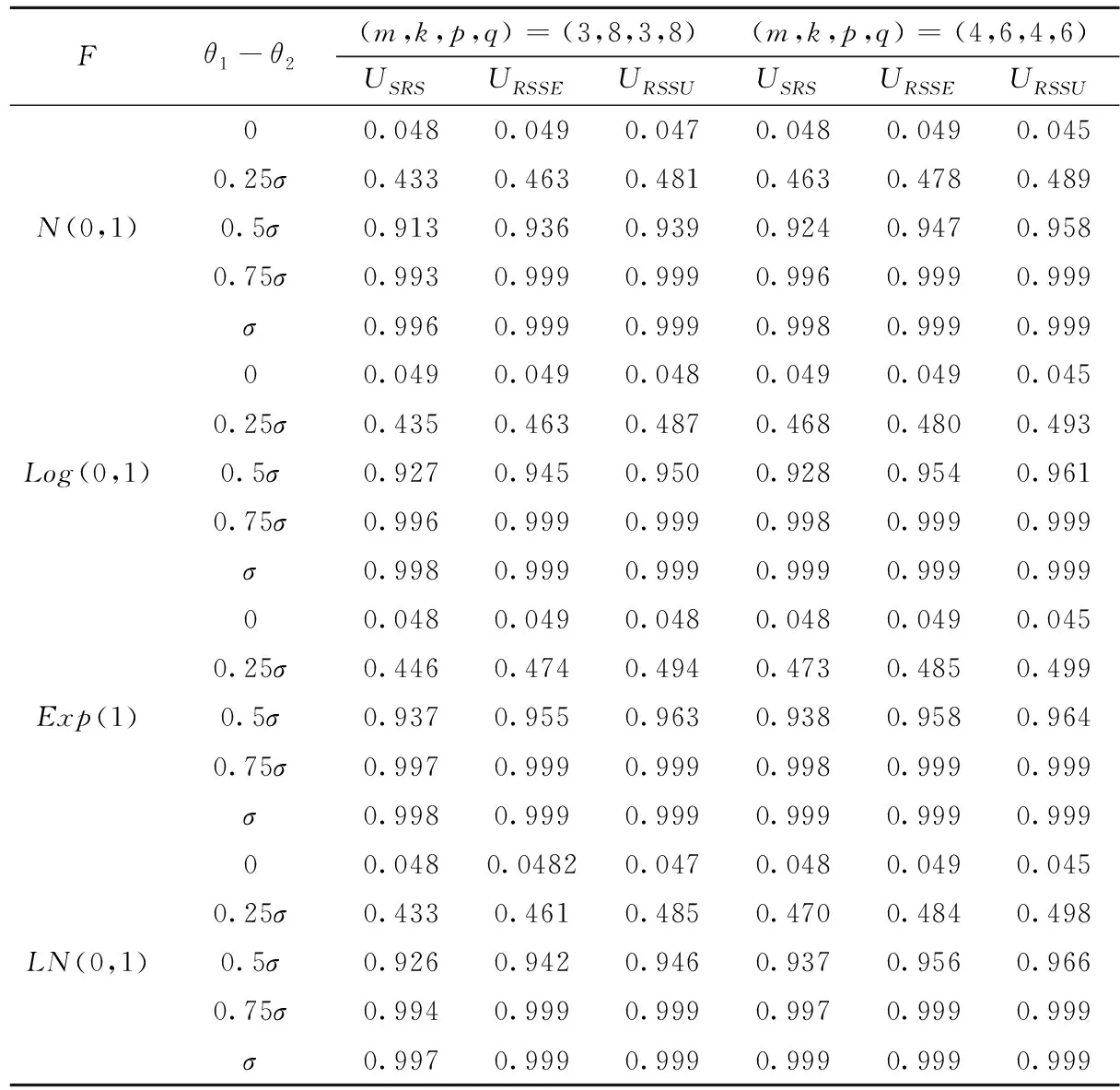
表2 Mann-Whitney检验的模拟功效