基于Excel软件实现四参数logistic模型在生物活性测定中的规范化应用

段徐华 ，王鸣人 ，凌今 ，邵泓 ，陈钢

1.上海市食品药品检验研究院国家局治疗类单抗质量控制重点实验室，上海 201203；2.复旦大学生物医学研究院，上海 200032

重组人粒细胞集落刺激因子（recombinant human granulocyte colony-stimulating factor，rhG-CSF）主要用于放化疗及骨髓移植后中性粒细胞减少症［1-2］。目前，《美国药典》（USP）、《欧洲药典》（EP）、《英国药典》（BP）、《印度药典》（IP）、《日本药局方》（JP）及《中国药典》三部（2015版）均收录了 rhG-CSF［3-8］，但各国药典对该制品生物学活性测定的试验数据处理采用的统计分析方法不尽相同。国外药典均采用基于直线模型的量反应平行线测定法，该方法对试验数据进行线性拟合后，采用方差分析进行可靠性测验［2-6］，在可靠性成立的条件下，以共斜率的方式将直线平行化后按等反应剂量比值计算供试品的相对效价，而《中国药典》三部（2015版）通则中rhG-CSF生物活性检测系采用基于S形logistic曲线模型的四参数回归计算法，该统计方法目前尚未收载于现行版《中国药典》生物检定统计法中，在进行试验数据处理时也未对可靠性测验作出要求。另外，USP、EP、BP及IP中rhG-CSF相对效价限度均为80%～125%，JP为 70%～140%，《中国药典》三部（2015版）为80%～150%［3-8］；效价置信区间 USP 规定为测定值的75%～133%，EP、BP、IP均规定为测定值的74%～136%［3-6］，各国药典置信区间宽度限度中USP为 ≤29%，EP、BP、IP均为 ≤31%，JP为 ≤30%，而《中国药典》未作规定。由此可见，《中国药典》对生物活性测定数据的可靠性判断及实验误差大小的控制与国际标准尚存在一定差距，而生物活性是反映药品有效性的重要指标，与产品质量密切相关，且中国大部分法定标准中生物活性的统计分析方法均为四参数回归计算法，因此，对四参数回归计算法的试验数据分析流程进行规范化研究具有重要意义。

本研究拟以rhG-CSF生物活性测定研究数据的四参数回归分析为例，参照量反应平行线测定法的计算思路，采用方差分析法进行可靠性测验，在可靠性成立的条件下，以共斜率及共渐进线的方式进行S形曲线的平行化，构建平行曲线模型（也称约束模型）进行供试品相对效价的计算［9-11］，并参照EP及BP中置信区间估计方法计算效价的置信区间。按上述设想建立配套的Excel分析模板，比较其与国际公认的统计分析软件SoftMax及PLA分析结果的一致性。同时，采用EP中收载的四参数回归计算法实例数据对其进行验证，以期为分析软件的选择提供依据。

1 材料与方法

1.1 试验数据及分析软件 研究数据1来自A企业提供的20130704批rhG-CSF生物学活性测定数据（表1）；研究数据2来自EP第5.3章5.4.1节四参数回归计算法破伤风抗血清效价测定实例数据［10］（表 2）；软件 Excel 2010、SoftMax Pro.6.5.1 及 PLA 3.0分别由美国Microsoft公司、美国Mole-cular Devices公司和德国Stegmann公司提供。

表1 rhG-CSF生物学活性测定（NFS-60细胞／MTT比色法）试验数据（A570／630）Tab.1 Readouts by microplate reader for rhG-CSF bioassay（NFS-60 cell／MTT）（A570 ／630）

表2 EP 5.4.1破伤风抗血清效价测定试验数据（A值）Tab.2 Experimental data on potency of tetanus antiserum in EP 5.4.1（A value）

1.2 四参数logistic模型拟合 四参数logistic模型常用的一种方程形式如下。

y=D+（A-D）／［1+（x／C）B］

式中y表示反应值；x表示药物作用浓度；A、B、C、D为4个特征性参数，其中A为反应下渐进线，D为反应上渐进线，B为曲线斜率因子，C为半数有效浓度（median effective concentration，EC50）［9，12］。

软件Excel采用规划求解功能进行四参数logistic自由模型与约束模型的拟合，其中自由模型分别进行标准品与供试品曲线4个参数的独立拟合，而约束模型中标准品与供试品曲线的参数A、B、D保持相同，参数C分别进行独立拟合。按以下原则进行A、B、C、D参数初始值赋值：A设置为比所有反应值中最小值略低的值，D设置为比所有反应值中最大值略高的值；四参数logistic模型方程式经logit转换后，对 ln［（A-D）／（y-D）］与 lnx 进行线性回归，若以b及γ分别表示回归方程的斜率和截距，则B可赋值为 b，C 可赋值为 e（-γ／b）［13］。

用软件Softmax及PLA相应内置程序对研究数据1分别进行标准品和供试品剂量反应曲线自由模型拟合及约束模型拟合。

1.3 方差分析及可靠性测验

1.3.1 方差分解思路 根据量反应平行线测定法利用平行化直线模型计算供试品效价的思路，四参数回归计算法利用约束模型计算效价的前提是方差分析显示约束模型拟合试验数据与自由模型无显著性差异，即可用约束模型代替自由模型进行数据处理及效价计算。

基于该计算思路，可将约束模型的总变异分解为试品间、回归项及残差项变异；约束模型的残差项变异又可分解为自由模型的残差项变异和偏离平行项变异；自由模型的残差项变异又可分解为模型失拟项变异及纯误差项变异［14］。各变异项满足如下关系。

差方和总=差方和试品间+差方和回归+差方和残差Ⅰ；

差方和残差Ⅰ=差方和残差Ⅱ+差方和偏离平行；

差方和残差Ⅱ=差方和模型失拟+ 差方和纯误差

式中差方和残差Ⅰ为标准品和供试品约束模型的残差平方和；差方和残差Ⅱ为标准品和供试品自由模型的残差平方和。

1.3.2 方差分析公式 根据1.3.1项方差分解的思路以及各变异项所反映的意义，列出各项变异的差方和与自由度（f）的计算公式［15-18］，计算各变异项的方差（各变异项差方和／各变异项自由度）。

1.3.3 数据分析 将①～⑧公式编辑入Excel软件，建立配套的分析模板；对研究数据1分别采用建立的Excel分析模板、软件SoftMax及PLA相应内置程序进行方差分析及可靠性测验。其中SoftMax不具备回归项和模型失拟项可靠性测验函数，仅进行偏离平行性分析。

1.4 相对效价及置信区间计算

1.4.1 相对效价 按生物检定中等反应剂量对比原则，研究数据1的相对效价R按约束模型中标准品与供试品拟合曲线EC50的比值计算，在Excel中建立相应计算模板。Softmax及PLA内置程序按该原则进行相对效价计算。

1.4.2 置信区间估计 按EP第5.3章4.2.节工作表4.2.1-Ⅰ和 4.2.1-Ⅱ及计算公式4.2.3-2在Excel中建立计算效价95%置信区间的表格模板［19］，软件Softmax及PLA分别选择profile（t distribution）法和基于约束模型进行方差分解的分析模式计算置信区间。比较3种软件计算研究数据1相对效价置信区间的一致性。

1.5 Excel计算模板的验证 对研究数据2分别采用建立的Excel计算模板及软件PLA进行数据分析，对各软件计算结果及EP报告值进行一致性比较，验证Excel计算模板的准确性。由于EP第5.3章5.4.1节实例可靠性测验采用加权卡方检验法，而Excel分析模板中的可靠性测验为参照常规量反应平行线测定法建立的方差分析法，因此其可靠性测验结果选择与PLA软件中分析结果相比较。

2 结果

2.1 四参数logistic模型拟合 结果显示，Excel与Softmax及PLA对各参数的估计值基本一致。若以不同软件各参数估计值的相对偏差（测量的偏差占平均值的百分比）计，最大相对偏差为0.08%，可忽略不计。见表3。

表3 标准品及供试品自由和约束模型拟合曲线中各参数的估计值Tab.3 Estimation of parameters in free model and constrained model for standards and test samples

2.2 方差分析及可靠性测验

2.2.1 方差分析 残差Ⅱ方差用以进行试品间、回归及偏离平行3项变异的F统计量的计算，误差项的方差用来进行模型失拟的F统计量的计算，Excel方差分析结果见表4。

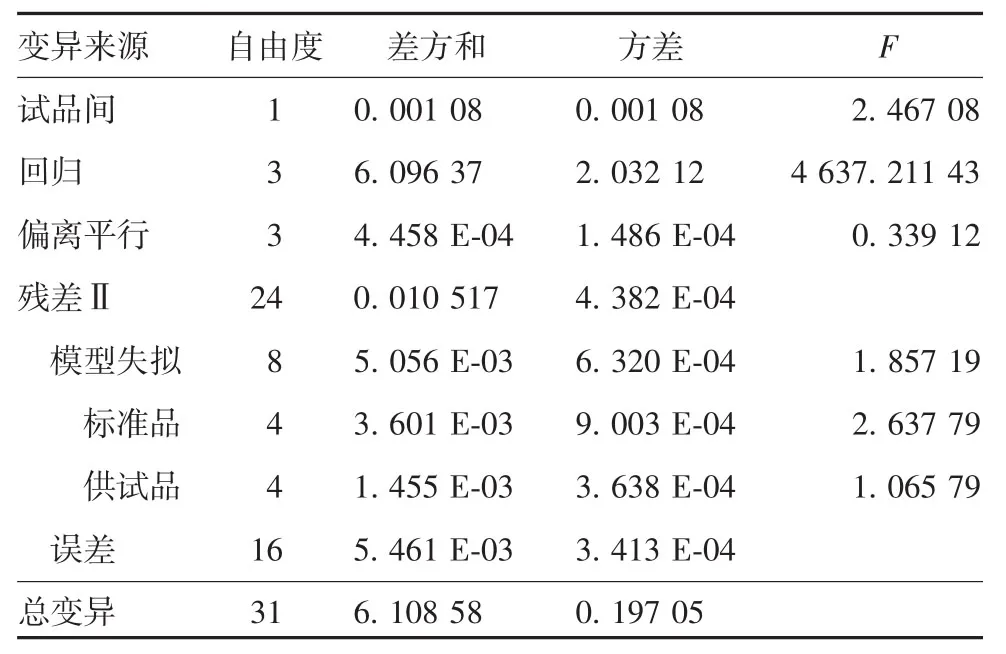
表4 Excel方差分析Tab.4 Analysis of variance by Excel software

2.2.2 可靠性测验及判断 对表4中方差分析数据进行各项变异显著性F测验，使用Excel中FDIST（Fstat，df1，df2）函数计算概率 P 值，其中 Fstat为表4中F值，df1为F值计算公式中分子项的自由度，df2为分母项的自由度。Excel可靠性测验结果与Softmax及PLA相应结果基本一致，回归项非常显著（P＜0.01）；偏离平行及模型失拟项均不显著（P均＞0.05），判定可靠性测验结果成立。见表5。

表5 Excel、Softmax及PLA软件的可靠性测验Tab.5 Tests of validity by Excel，Softmax and PLA software

2.3 相对效价及置信区间计算

2.3.1 相对效价 研究数据1中标准品和供试品拟合曲线的EC50即为表3中约束模型下Excel拟合的C值，R为103.9%（26.08／25.10×100%）。

2.3.2 置信区间估计 3种软件计算效价的95%置信区间均为98.3%～109.7%，其相对置信区间均为94.6%～105.6%，表明3种软件计算结果一致。

2.4 Excel计算模板验证 结果显示，Excel曲线拟合结果、效价及置信区间计算结果与EP报告结果一致，可靠性测验结果与PLA分析结果一致，见表6。

表6 Excel分析结果与EP报告及PLA分析结果的比较Tab.6 Comparison of analysis result by Excel software with reported result in EP and analysis result by PLA software

3 讨论

本研究以rh-GCSF生物活性测定数据的分析为例，参照量反应平行线测定法中以平行化直线模型计算效价的思路，针对四参数回归计算法，提出采用平行化曲线模型作为效价计算模型的设想。该设想的前提是实验结果的可靠性需成立。量反应平行线测定法的可靠性测验主要是基于变异来源进行各变异项的方差分析，包含在一定概率水平下试品间、回归项、偏离平行项及偏离直线项的F检验。通过分析量反应平行线测定法中各变异项所反映的实际意义，可构建出四参数回归计算法中对应的变异分析项：试品间、回归项、偏离平行项及模型失拟项，进而通过对各变异项的方差分析进行可靠性判定。

置信区间宽度反映的主要是实验精密度，置信上下限的间距越宽表明实验误差越大，反之误差越小。因此，报告相对效价的置信区间可利于监控实验误差大小是否在可接受范围内，从而获得准确可靠的结果。量反应平行线测定法中效价置信区间的计算多是基于适用于直线模型的Fieller理论［20］，由于四参数回归计算法中拟合模型为S形曲线模型，因此，本研究参照EP 5.3章5.4.1节四参数回归计算法实例，先通过对响应值进行logit转换，将S形曲线直线化，再按照直线模型计算效价置信区间的方式获得其95%置信区间［10］。

本研究覆盖了生物活性测定数据四参数回归分析的3个核心环节：四参数logistic回归模型拟合、可靠性测验、相对效价和置信区间估计。整个过程涉及大量运算工作，本文对Excel、Softmax及PLA软件进行了比较，其中Softmax为美国Molecular Devices公司酶标仪自带软件，在国内较为常用；PLA为德国Stegmann公司开发，在欧美国家常用，目前已获得国外监管机构的认可。经比较，3种软件计算的结果基本一致；同时采用EP 5.4.1四参数回归计算法实例数据对建立的Excel分析模板进行验证，所建立模板的分析结果与EP报告结果也一致，表明其分析结果可靠。目前，Excel和PLA软件涵盖了所有计算功能，可实现从剂量反应曲线的拟合至相对效价及置信区间估计的全过程运算。因Excel本身四参数拟合和计算功能并未得到开发，需通过大量计算公式的编辑及函数的调用才能建立分析模板，过程繁琐，数据处理量大，容易出错，基于此局限性，本实验室目前正致力于自动化计算软件的开发。PLA在导入试验数据后即可通过一键自动化得到结果，操作简便，但价格昂贵，且要求应用人员具备一定的统计学基础。Softmax内量的方差分析功能目前仅限于平行性检验，尚不包括试品间、回归项和失拟项的显著性检验，需进一步在Softmax软件中编辑相关公式才方便使用。因此，建议不同检测单位可根据各种软件获得及分析的便捷性选择适宜的分析软件。

基于量反应平行线测定法的计算思路，本研究构建四参数回归计算法的效价计算设想，实现了从直线模型至S形曲线模型计算思路的沿革；并基于目前实验室应用最普遍的Excel软件，实现了分析模板的建立与验证，深入剖解了四参数回归计算法从拟合至置信区间估计每个步骤中的计算公式，为自动化计算软件的开发奠定了基础，旨在推动四参数回归计算法在生物活性测定中的规范化应用。