基于遗传算法的共轭凸轮机构计算机辅助设计*
2021-02-25葛乐乐胡凯文
葛乐乐,张 龙,胡凯文
(南京理工大学 机械工程学院,江苏 南京 210094)
0 引 言
两个凸轮固结在同一回转轴,分别称为主凸轮和回凸轮,用于控制从动件的推程与回程,固结的两凸轮称为共轭凸轮,一般将控制从动件推程的凸轮称为主凸轮。共轭凸轮机构因其传动精确,能够精确控制机构从动件的推程和回程,被广泛应用于打纬、开口、引纬等精密机械中[1,2]。
为了保证共轭凸轮机构的精确性,需要设计有较高精度的凸轮廓曲线。凸轮机构的设计方法大致分为图解法和解析法两大类。图解法的设计任务量比较大,而且不能满足设计精度的要求;因此,大多采用解析法,利用计算机进行求解。
蔡汉明等[3]使用C#语言对AutoCAD进行了二次开发,得到了凸轮轮廓曲线的DWG格式文件,实现了共轭凸轮的参数化设计;魏奔等[4,5]为了实现共轭凸轮机构满足许用压力角的要求,利用MATLAB开发计算机辅助设计软件,通过人机交互的方式获得了凸轮廓线特征点数据;LIU Qing-li等[6]使用Creo软件输入公式生成凸轮轮廓曲线,实现了共轭凸轮的参数化设计,并对机构进行了运动仿真,验证了从动件运动规律;赵晓芬[7]在NX5草图环境下,利用弗洛克近似法求解,确定了凸轮机构的基本尺寸,通过输入轮廓曲线表达式生成了凸轮草图,拉伸生成了凸轮三维模型。上述方法不能实现共轭凸轮机构压力角最小化,不能使机构的传动效率达到最优;而且,以上方法只能得到凸轮的轮廓曲线特征点或零件图,不能直接获得凸轮的三维模型。
本文建立最大压力角最小化的优化模型,采用遗传算法进行求解,得到共轭凸轮机构的基本尺寸,编写指令式共轭凸轮机构计算机辅助设计软件,对SolidWorks进行二次开发,并对机构进行ADAMS仿真验证。
1 共轭凸轮机构的数学模型
1.1 从动件运动规律曲线
以凸轮的角位移(φ)为x轴,以从动件的角位移(ψ)为y轴,绘制函数ψ=f(φ),所得曲线称为凸轮机构从动件运动规律曲线。一般来说,从动件规律的给出方式有两种:
(1)将从动件运动规律曲线分解成若干段,每一段以标准传动函数的形式给出,标准传动函数通常选取:休止运动、多项式运动规律、简谐加速度运动规律,等[8];
(2)以离散点{φi,ψi},{dψ/dφ}来表示运动特性曲线。
本文计算实例的从动件运动规律以方式1给出,从动件运动规律如表1所示。
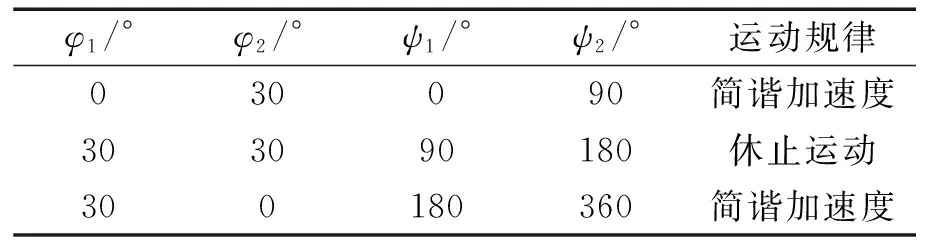
表1 从动件运动规律
1.2 凸轮机构的压力角
凸轮机构压力角是机构最重要的参数之一,对机构的传动效率有着重大影响。
凸轮机构压力角示意图如图1所示。

图1 凸轮压力角示意图
图1中,O为凸轮转动中心,A为摆杆的转动中心,凸轮与摆杆接触点处的公法线与OA连线交于点P,可知P为摆杆从动件与凸轮的瞬心;凸轮与摆杆在P点处的速度大小相等,速度方向相同。所以,当凸轮的转动方向与摆杆转动方向相反时,当且仅当P点在OA的连线上,凸轮与摆杆在P点的速度方向才相同;同理,当凸轮的转动方向与摆杆转动方向相同时,当且仅当P点在OA的延长线上,凸轮与摆杆在P点的速度方向才相同。
过P点作PC⊥AB,则有∠BPC=α,即机构此时的压力角。可得压力角满足:
(1)
式中:LBC—BC的长度;LPC—PC的长度。
其表达式分别为:
LBC=LAP·cos(ψG-ψ)-LAB
(2)
LPC=LAPsin(ψG-ψ)
(3)
式中:LAP—AP的长度;LAB—AB的长度;ψG—摆杆初始时刻与y轴负半轴的夹角。
其表达式为:
(4)
因为P点为摆杆与凸轮的瞬心,根据瞬心的定义有:
(5)
根据图1可得:
(6)
式中:η—转向标志量,当凸轮转向与摆杆转向相同时η=1,当凸轮转向与摆杆转向相反时η=-1。
根据式(1~5),压力角可改写为:
(7)
1.3 凸轮廓线的数学模型
对于给定的{φi,ψi},可以利用反转法与机构学的知识得到凸轮廓线的数学模型。
共轭凸轮廓线求解示意图如图2所示。
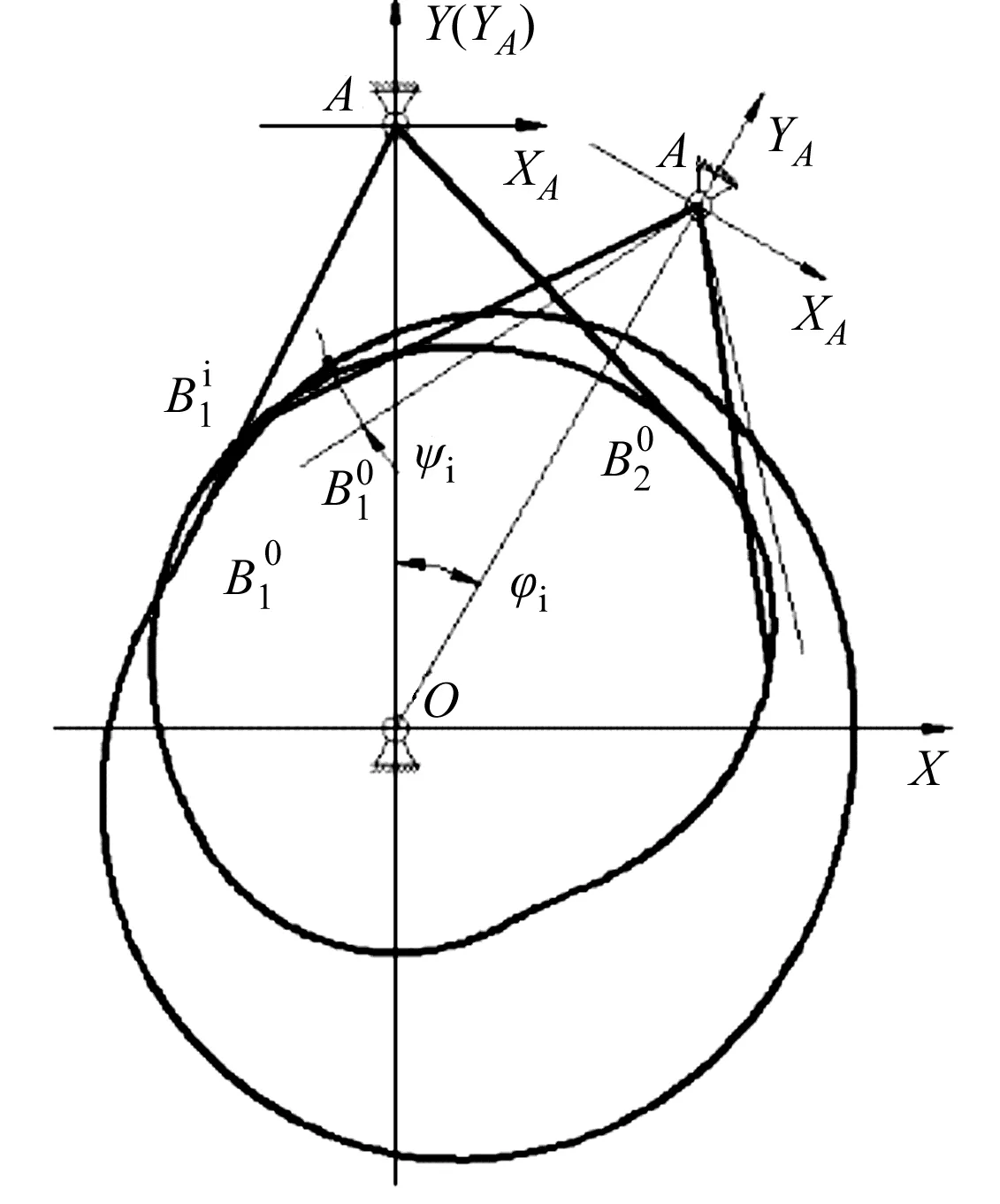
图2 共轭凸轮廓线求解示意图
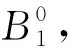
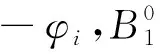
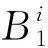
(8)
式中:α—凸轮机构中心矩;L1—摆杆1的长度。
所以,可得主凸轮的理论廓线坐标方程:
(9)
同理,回凸轮的理论廓线坐标方程为:
(10)
式中:L2—摆杆2的长度。
则凸轮的实际廓线坐标方程:
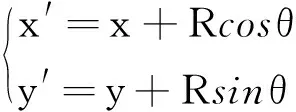
(11)
式中:R—滚子半径;θ—理论轮廓曲线对应点处法线的升角。
(12)
因为计算机的离散性,本文将表1从动件运动规律曲线离散化,得到一系列离散点,将其代入上述公式,便可得到凸轮轮廓曲线的离散点。
2 优化计算与分析
2.1 遗传算法简介
遗传算法是20世纪60年代末期由Michigan大学教授JOHN H提出的一种模拟生物进化机制来进行全局优化搜索的算法[9]。与传统的梯度下降算法等优化方法相比,遗传算法并不要求计算目标函数的梯度,对目标函数的凹凸性也相对要求较低,这些使得遗传算法可以更加有效地解决优化问题。
遗传算法的计算过程一般分为:初始化种群,每个个体按二进制或十进制进行编码;计算每个个体的适应度,通常是由目标函数进行变换得到的;根据个体的适应度,利用交叉算子和变异算子对种群进行更新,直至优化准则得到满足,结束计算。
本文以种群大小为100,交叉概率0.8,变异概率0.2进行遗传算法求解。
2.2 优化模型
共轭凸轮的基本尺寸主要有:
中心矩α,基圆半径rG,摆杆1长度L1,摆杆2长度L2,摆杆夹角αR,滚子半径rR,通常有L1=L2=L,本文中αR=100°,rR=7。
基本尺寸主要根据压力角来确定,基本尺寸选取不好,可能会导致机构压力角过大、传动效率降低、更容易磨损。通常确定凸轮机构基本尺寸的方法,主要是根据许用压力角的要求,使用作图法确定基本尺寸。但是,这种方法并不能使得机构的压力角达到最小,不能使机构的传动效率达到最优。
本文采用遗传算法的优化方法,以最小化凸轮机构的最大压力角为优化目标,建立相应的约束方程,进而求解机构的基本尺寸。
优化模型的目标函数为:
min: max(α1(X,φi,ψi),α2(X,φi,ψi))
(13)
式中:X—优化模型决策变量,X=[x1,x2,x3]=[α,rG,L]。
压力角计算见式(6),决策变量的取值范围需要根据机构的工作空间进行确定,本文取下限为[20,20,15],取上限为[45,30,30]。
因为决策变量需要构成三角形,所以应该有约束方程:
(14)
2.3 计算与分析
本文利用遗传算法对优化模型进行三次求解,遗传算法计算结果如表2所示。
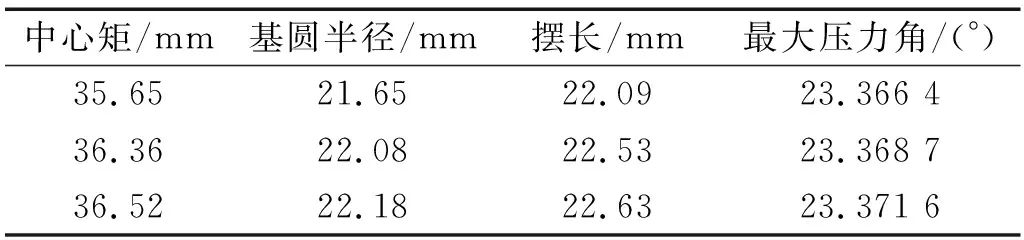
表2 遗传算法计算结果
由表2可以看出:算法每次计算求得的目标函数的差距不超过0.1°,说明遗传算法具有较好的稳定性。
选取第一组解的结果进行分析。第一次优化,其每代适应度的均值与最优值随遗传算法迭代次数的优化收敛图如图3所示。
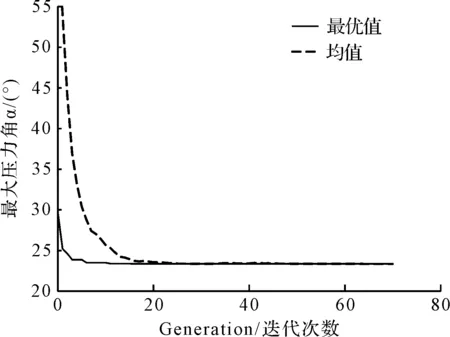
图3 共轭凸轮参数优化收敛图
从图3可以看出:算法在第20代左右即达到了最优值,之后的迭代计算也没有出现大幅度波动,可以看出遗传算法具有较好的收敛性。
因为本文的决策变量有3个,为了能更直观地分析遗传算法的准确性,现令中心矩为第1次的优化结果α=35.65 mm;以基圆半径为x轴,摆长为y轴,绘制共轭最大压力角凸轮压力角等高线图,如图4所示。
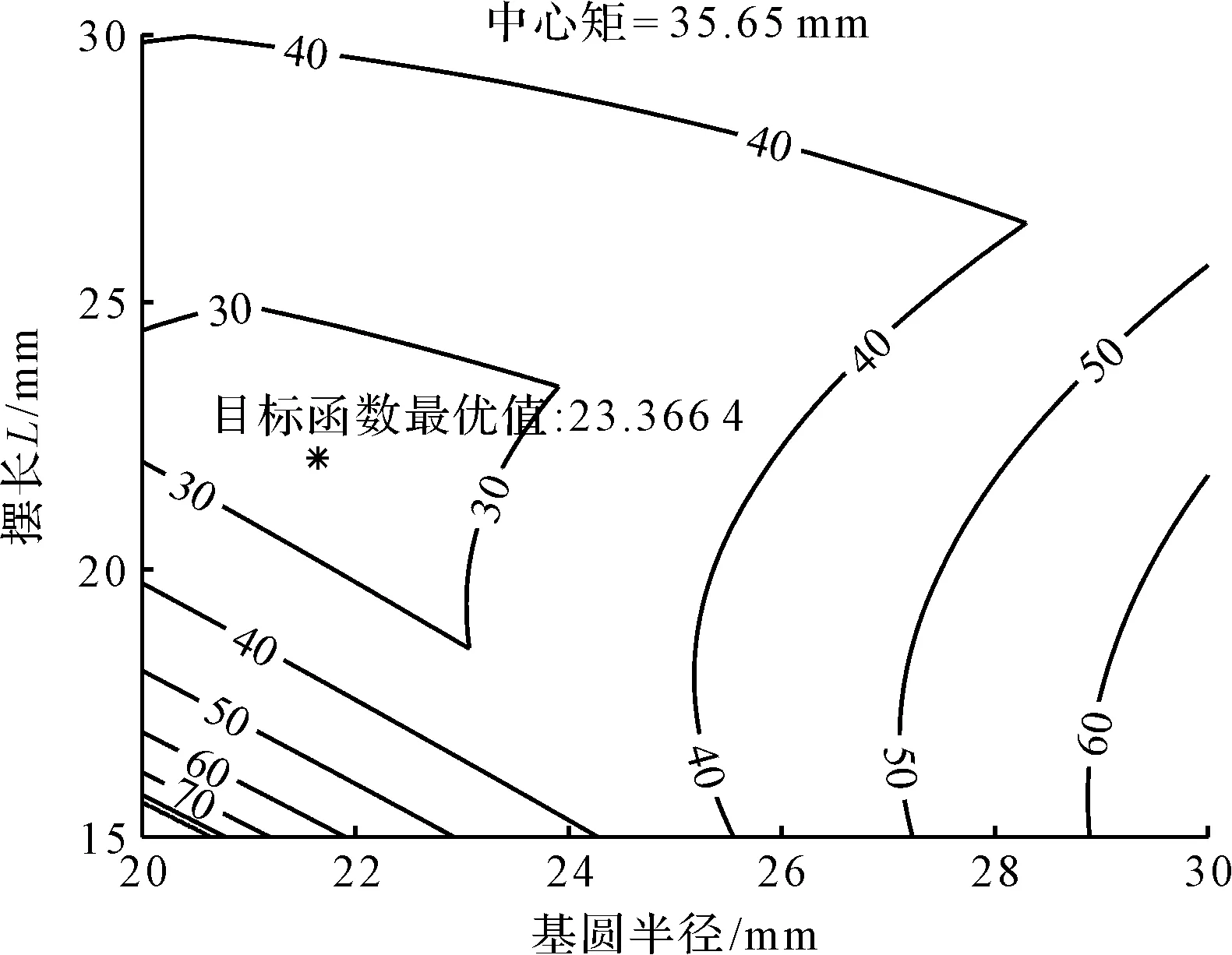
图4 共轭凸轮最大压力角等高线图
从图4中可以看出:当中心矩为35.65 mm时,目标函数最优值为23.366 4°,与遗传算法优化结果相同。由此可见,遗传算法求解具有较好的准确性。
3 软件设计与实例验证
3.1 辅助设计软件
本文使用MFC开发共轭凸轮计算机辅助设计软件[10],具体步骤为:
采用指令式的设计方法,将共轭凸轮机构设计的每个步骤设计成一个指令,将每一个共轭凸轮机构的设计抽象为一组指令程序;用户通过拖动的方式将指令集内的指令添加到指令程序内,软件给与每个指令相应的反馈;用户设计完成一个共轭凸轮机构时,一组对应的指令程序也就相应地编写完成,可以对该指令程序进行保存;保存好的指令程序可以在软件内打开,实现上次设计的重现。
共轭凸轮机构的数字化设计流程如图5所示。
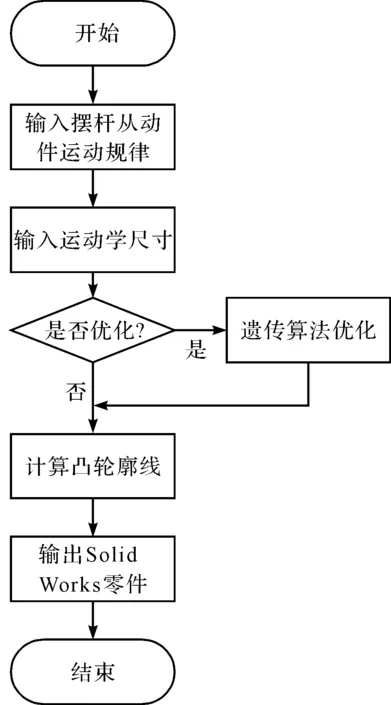
图5 共轭凸轮机构数字化设计流程
3.2 实例验证
本文以表1的运动规律为例,进行共轭凸轮的数字化设计实例验证。
添加输入从动件运动规律指令,可得运动规律输入界面,如图6所示。
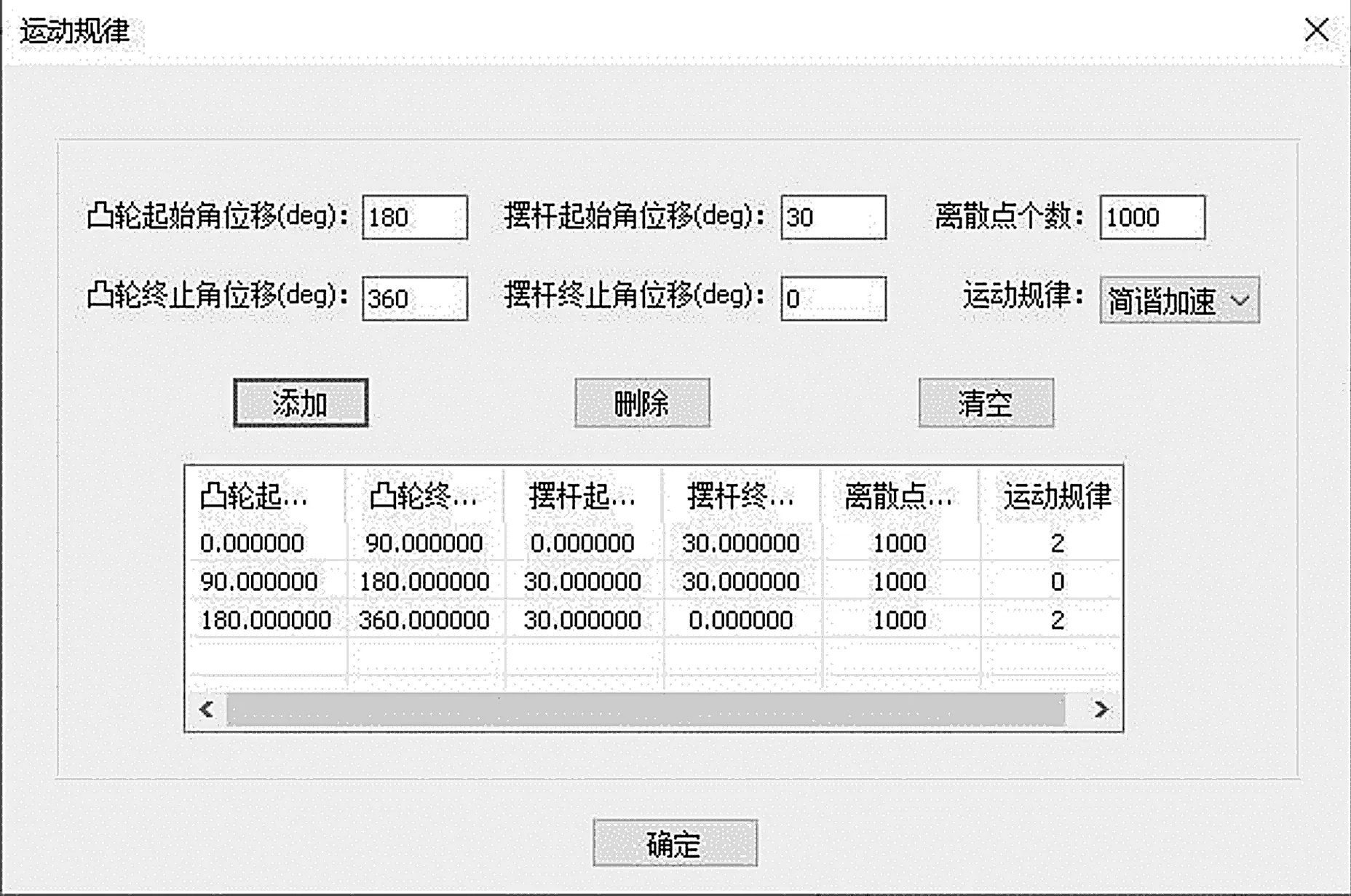
图6 运动规律输入界面
在图6对话框中输入从动件运动规律,然后添加输入基本尺寸指令,可得运动学尺寸参数输入界面,如图7所示。
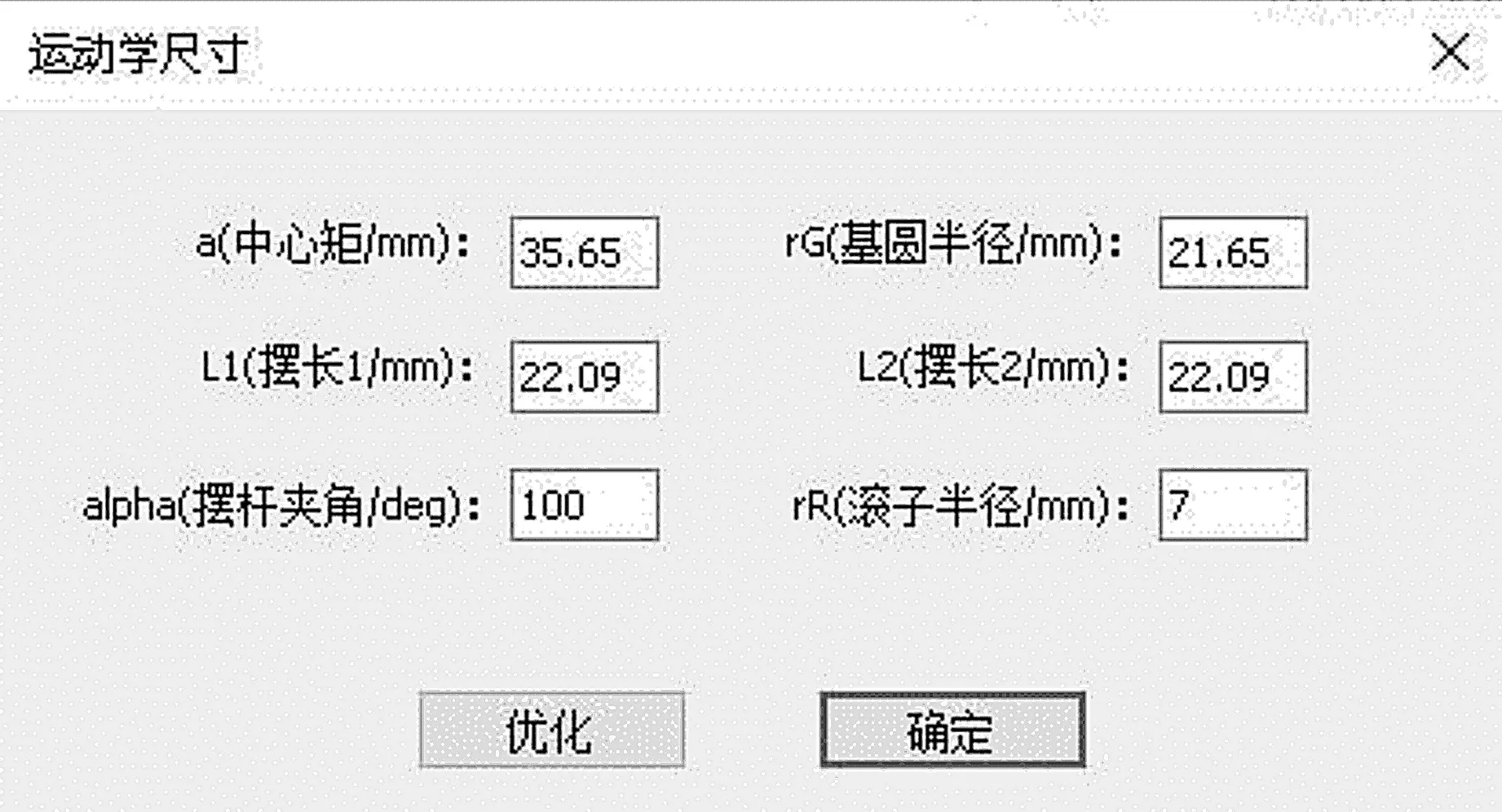
图7 运动学尺寸参数输入界面
在图7的对话框中输入基本尺寸参数,用户可以选择是否使用遗传算法进行参数的优化。遗传算法的参数优化可以利用Galib类库来实现[11]。输入参数之后,添加计算凸轮轮廓指令,计算完成之后可以在绘图区域内得到凸轮的轮廓曲线。
为了能够直接获得凸轮的三维模型,软件设有生成SolidWorks零件模型指令,实现SolidWorks二次开发。为了方便二次开发,SolidWorks提供了几百个API函数,这些函数使得程序员得以直接访问SolidWorks[12]。在MFC中要使用这些函数,只需要导入SolidWorks便可。添加生成SolidWorks零件模型指令后,SolidWorks软件便会自动启动,绘制凸轮的草图,进行拉伸后得到零件的三维模型。
其主要程序如下:
{
CComPtr
swApp.CoCreateInstance (__uuidof(SldWorks));
VARIANT_BOOL *visibility=NULL;
swApp -> get_Visible(visibility);
swApp -> put_Visible(TRUE);
IPartDocPtr myPart = swApp -> INewPart();
IModelDoc2 *m_pModelDoc;
myPart ->QueryInterface(&m_pModelDoc);
VARIANT_BOOL retval;
retval=m_pModelDoc->SelectByID(_T("前视基准面"),_T("PLANE"),0,0,0);
m_pModelDoc -> InsertSketch();
…
}
得到的共轭凸轮主、回凸轮三维模型如图8所示。
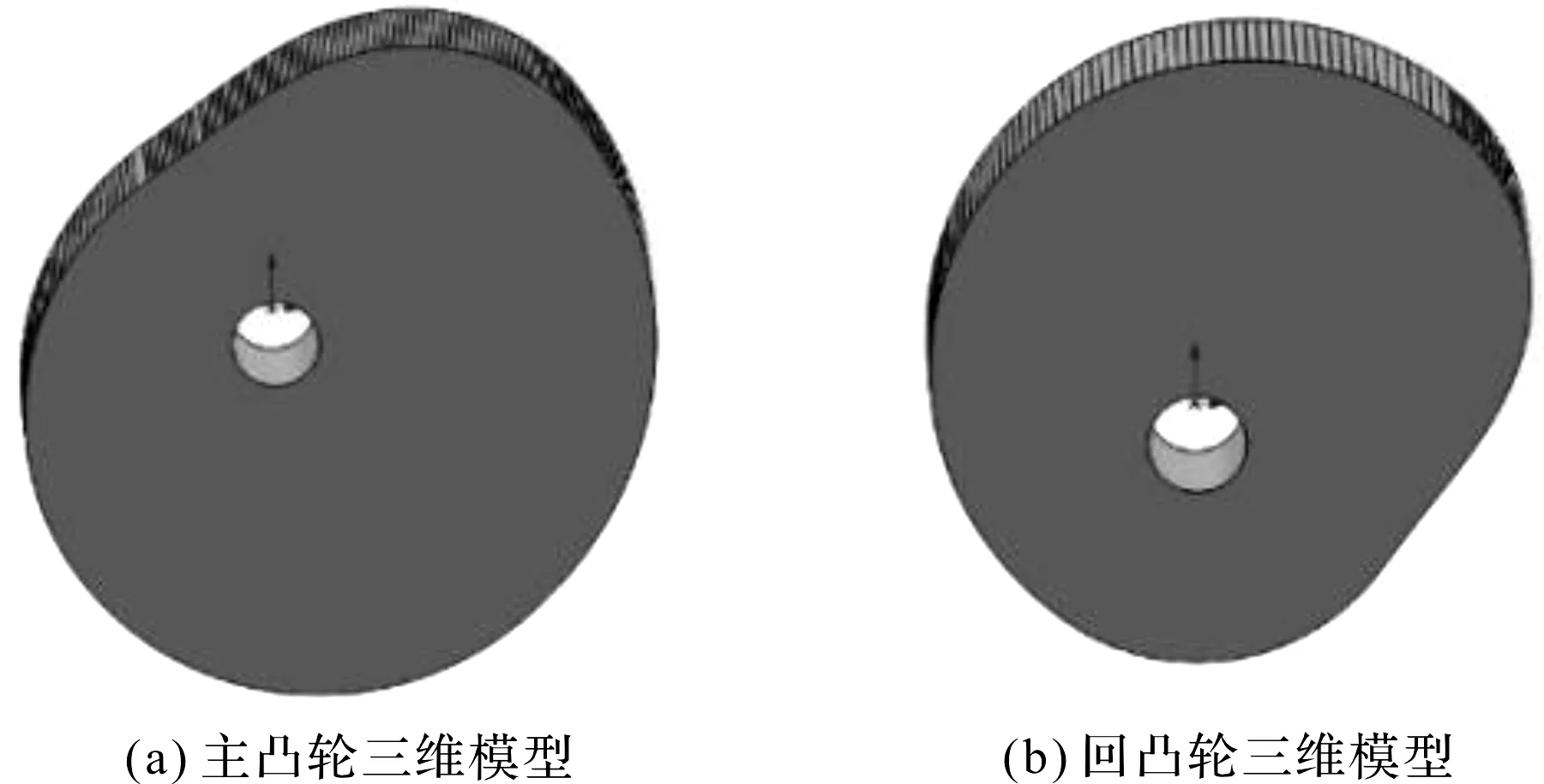
图8 主、回凸轮三维模型
至此便实现了一例共轭凸轮机构的数字化设计,同时软件也生成了一组指令程序,可以选择将其保存为TXT文件,方便下次打开,实现设计过程的复现。
4 运动仿真
为了验证软件计算的准确性,本文利用SolidWorks制作共轭凸轮机构的虚拟样机。将制作好的虚拟样机导入Adams,在凸轮、摆杆以及滚子的转动中心添加转动副,并给主凸轮和回凸轮添加固定约束;给主凸轮施加驱动,进行运动仿真,得到从动件运动规律。
与表1所给的从动件运动规律相比,可得运动规律的设计要求曲线与仿真曲线比较图,如图9所示。
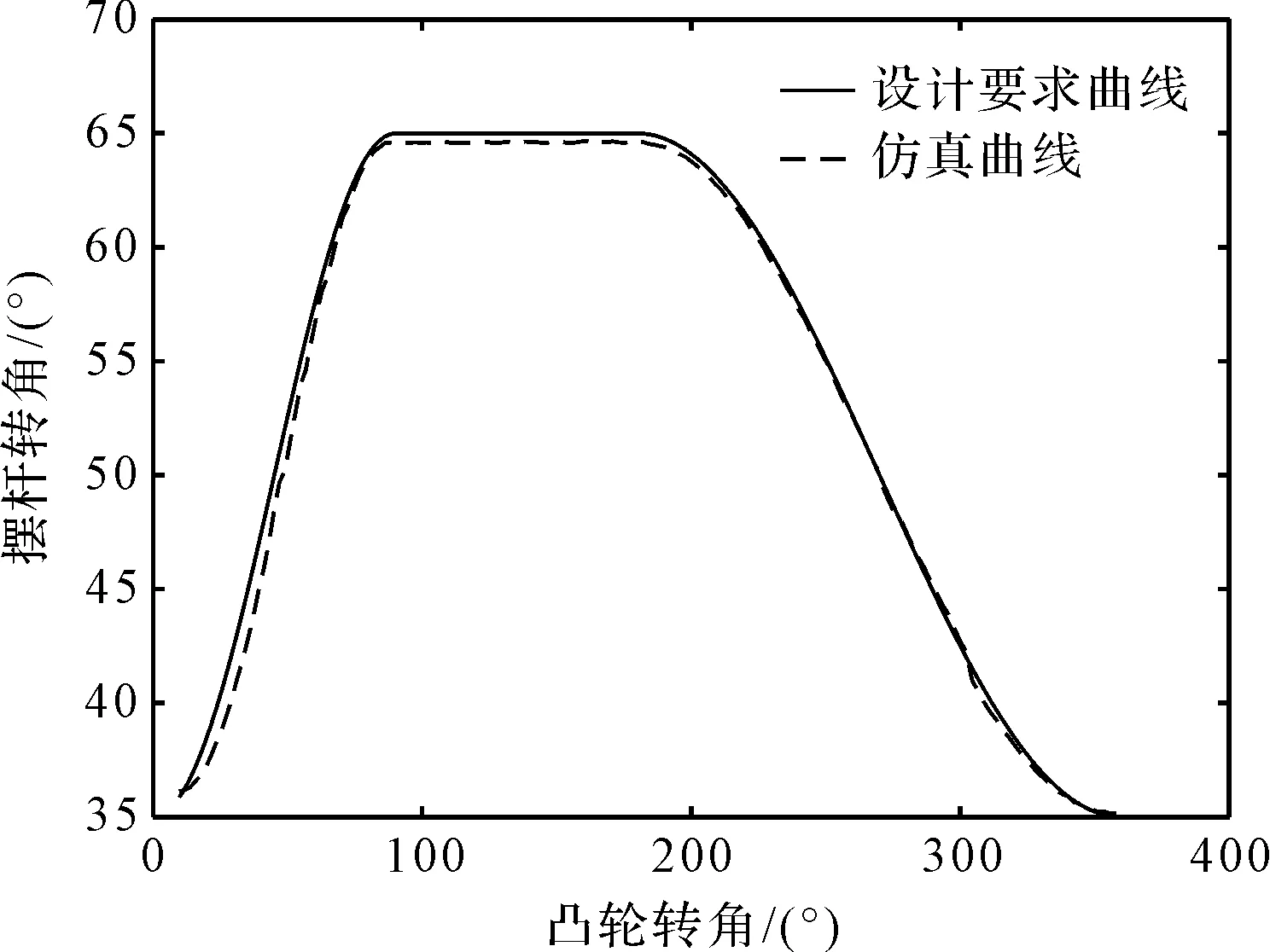
图9 设计要求曲线与仿真曲线的比较
从图9可看出:仿真曲线与设计要求曲线基本吻合,最大误差值为0.5°。由此可见,该软件所设计的共轭凸轮机构可以比较好地满足要求。
5 结束语
基于遗传算法的共轭凸轮机构优化设计的方法,笔者通过优化计算的方法,使得机构的最大压力角达到全局最优值附近,提高了机构的传动效率;对SolidWorks的二次开发,降低了机构设计的工作量;对设计结果进行仿真分析,检验了设计方法的正确性。
本研究给出的基于遗传算法的共轭凸轮机构的计算机辅助设计方法,为共轭凸轮的优化设计提供了理论工具和设计手段。这种方法在减轻设计工作量的同时,优化了机构的传动效率,使得共轭凸轮的设计更加自动化。
同时,本研究的不足之处,即共轭凸轮机构在实际使用中可能存在很多受制条件,在今后的研究中,需要考虑增加相应约束,改进算法,以实现更加通用的设计方法。
