直流偏磁下变压器绕组及垫块振动特性分析

李 华，李晓华，褚福源，黄 堃，林球英，王 尉

(1.广东电网有限责任公司广州供电局，广州 510245；2.上海电力大学电气工程学院，上海 200090)

由于超高压直流输电采用单极大地回流运行方式或城市轨道交通杂散电流等原因，会使变压器进入直流偏磁状态，此时变压器励磁电流受直流影响产生畸变，铁心进入饱和状态，变压器振动特别是绕组振动加剧，长时间运行在此工作状态下会对变压器产生不可逆损害[1]。高压直流输电的单极大地回流以及轨道交通的广泛普及决定了中国变压器受直流偏磁影响严重，对于直流偏磁下绕组振动特性的研究显得尤为重要。

直流偏磁下变压器的励磁电流受到影响，其中由于直流磁通的引入，变压器磁特性发生变化导致励磁电流发生畸变，产生尖顶波。由于变压器铁芯中的磁通并非直流磁通和交流磁通的简单叠加，且直流磁通因其时不变性难以通过测量获得，因此较难获得包含直流磁通的偏磁下的磁化曲线，通过简单迭代法能够解决这一问题[2-4]。

正常情况下，绕组具备一定的抗突发能力[5-6]，但是在直流偏磁下，绕组由于直流引入导致的磁特性变化，抗突发能力将降低，相比正常情况下更易发生塑性形变进而使绝缘层被破坏，降低使用寿命。因此对于绕组直流偏磁下振动特性的准确计算分析十分重要。但是目前多采用将绕组简化为忽略垫块结构的圆柱模型的建模方法，这样计算结果误差较大，且无法评估垫块状态。

针对绕组简化为忽略垫块结构的圆柱模型的建模方法误差较大这一问题，现建立绕组的电磁场-结构场-流体场耦合模型，通过对包含垫块的线饼式绕组分层精细化模型计算，对直流偏磁下绕组及垫块的振动特性进行分析。利用绕组和垫块振动特性对变压器直流偏磁下抗突发能力下降的原因进行分析。

1 变压器抗突发能力分析计算流程

绕组振动是以电磁力为主的受迫振动。直流偏磁发生时，励磁电流的畸变使得绕组内的电流首先发生变化，进而影响绕组振动特性。通常绕组模型简化为一个圆筒模型，忽略垫块等因素。垫块的状态正确判断是准确计算短路时绕组位移的重要前提，同时垫块也是绝缘的重要环节，绝缘垫块为渐刚性材料，非线性使得非同层不同位置的垫块的刚度不尽相同，使得其振动特性必然存在着差异。计算流程如图1所示。

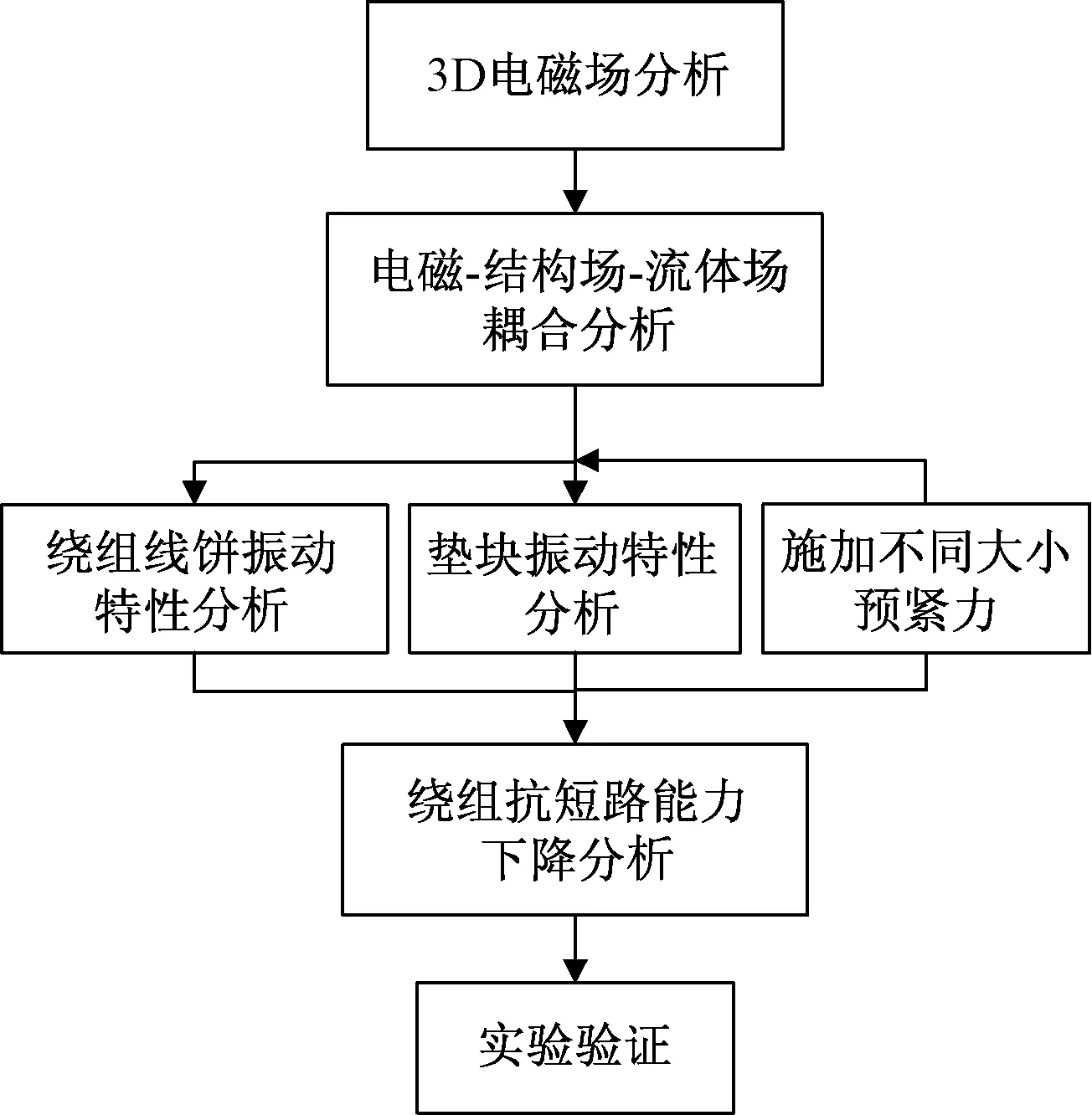
图1 绕组振动特性及垫块位移分析流程Fig.1 Winding vibration characteristics and pad displacement analysis process

具体计算流程如下：①建立绕组考虑分层及垫块的精细化计算模型；②进行三维电磁场分析计算；③电磁力与结构场耦合分析绕组及垫块振动特性；④实验验证。

以一台220 kV三相三柱式变压器为例，仿真模型如图2所示。为了节约计算内存，仅将中间相绕组建立为垫块模型，其余两相均采用简化模型进行计算。

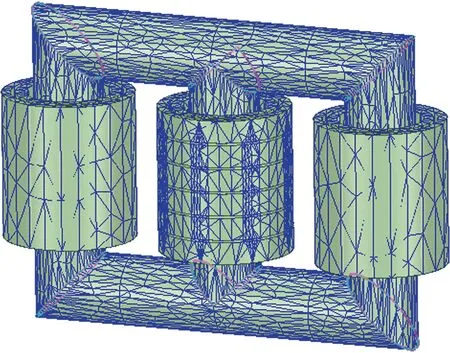
图2 直流偏磁下振动分析有限元模型Fig.2 Finite element model of vibration analysis under DC bias

2 绕组和垫块受力理论分析

2.1 绕组受力分析

变压器绕组所受电磁力与电流平方成正比，即随电流上升绕组振动加强；绕组振动基频为电流频率的2倍，一般为100 Hz[7]。

图3为绕组中垫块受力的示意图，可以看到垫块由于受到重力G和压力FN，因此会在线饼移动时，产生摩擦力。然而不同位置的线饼所受到的重力不尽相同，底层垫块会受到相比于顶层垫块更大的重力。

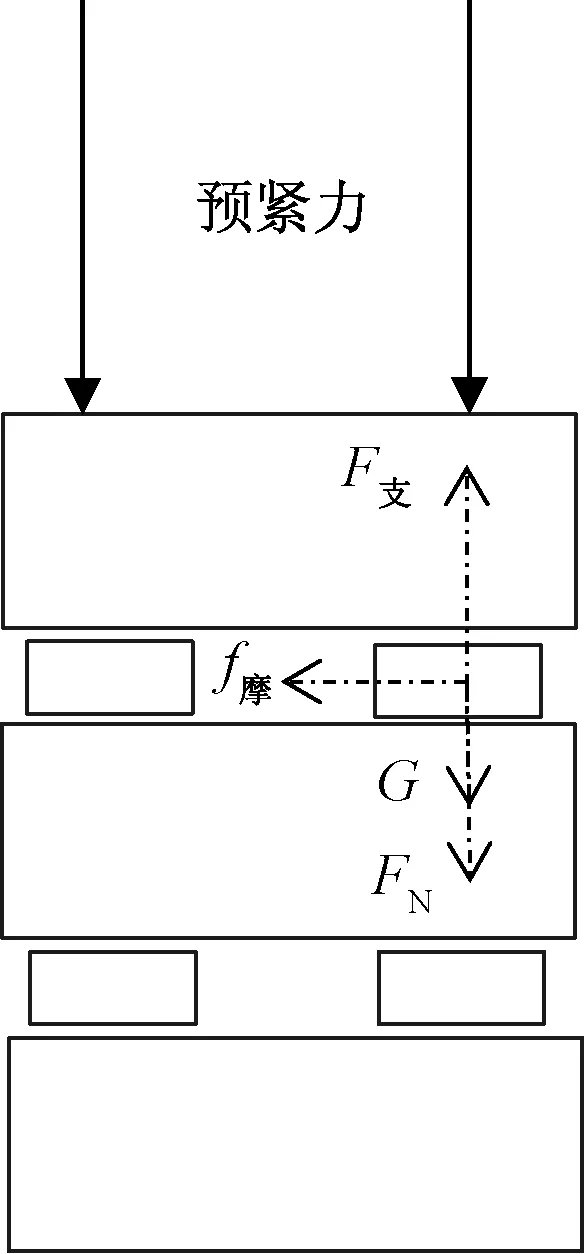
图3 垫块受力示意图Fig.3 Pad force diagram

在实际计算中变压器绕组弹簧力学模型是将绝缘垫块假设为弹簧，将一层层的绕组线饼假设为质量为m的小块，变压器绕组受轴向力振动时可将系统视为由弹簧和质量小块构成。各线饼之间垫块的弹性系数视为一致，均用K表示;绕组端部的绝缘垫块(绕组和压紧装置之间)的弹性系数以KB和KN表示;摩擦因数用C表示;第n个单元相对于本身原先位置的位移用zn表示;质量小块用m表示，变压器绕组的位移用z表示，绕组所受的力用F表示。建立弹簧力学模型的数学表达式，即

(1)

绝缘垫块为渐刚性材料，其非线性特性使得其刚度随着预紧力和振动受力的变化而实时改变，因此不同层垫块的刚度将不尽相同。其应力-应变关系[8]在一定范围内可表示为

σ=aε+bε3

(2)

式(2)中：σ为应力；ε为应变；a、b为硬化系数,a=1.05×102MPa；b=1.75×103MPa。

(3)

正确模拟垫块的刚度非线性特性是仿真关键，其杨氏模量的非线性使得非同层相同位置的垫块刚度不尽相同，其振动特性必然存在着差异。

2.2 趋肤效应对绕组受力的影响

趋肤效应使得电流集中在导体表面有限空间内，增大有效电阻。距离较近导体通以高频交变电流时，导体将受到附近其他导体电流产生的磁场影响，这种现象称为邻近效应。根据磁约束模型，电荷由于洛伦兹力的作用，不仅会向一侧聚集，同时会有部分电荷围绕磁感应线作螺旋式运动，导致电流密度在导线截面延周边堆积。由于漏磁的增加，必然导致绕组的趋肤效应和邻近效应更为严重，直接导致小面积内绕组受力的大小改变，如图4所示。

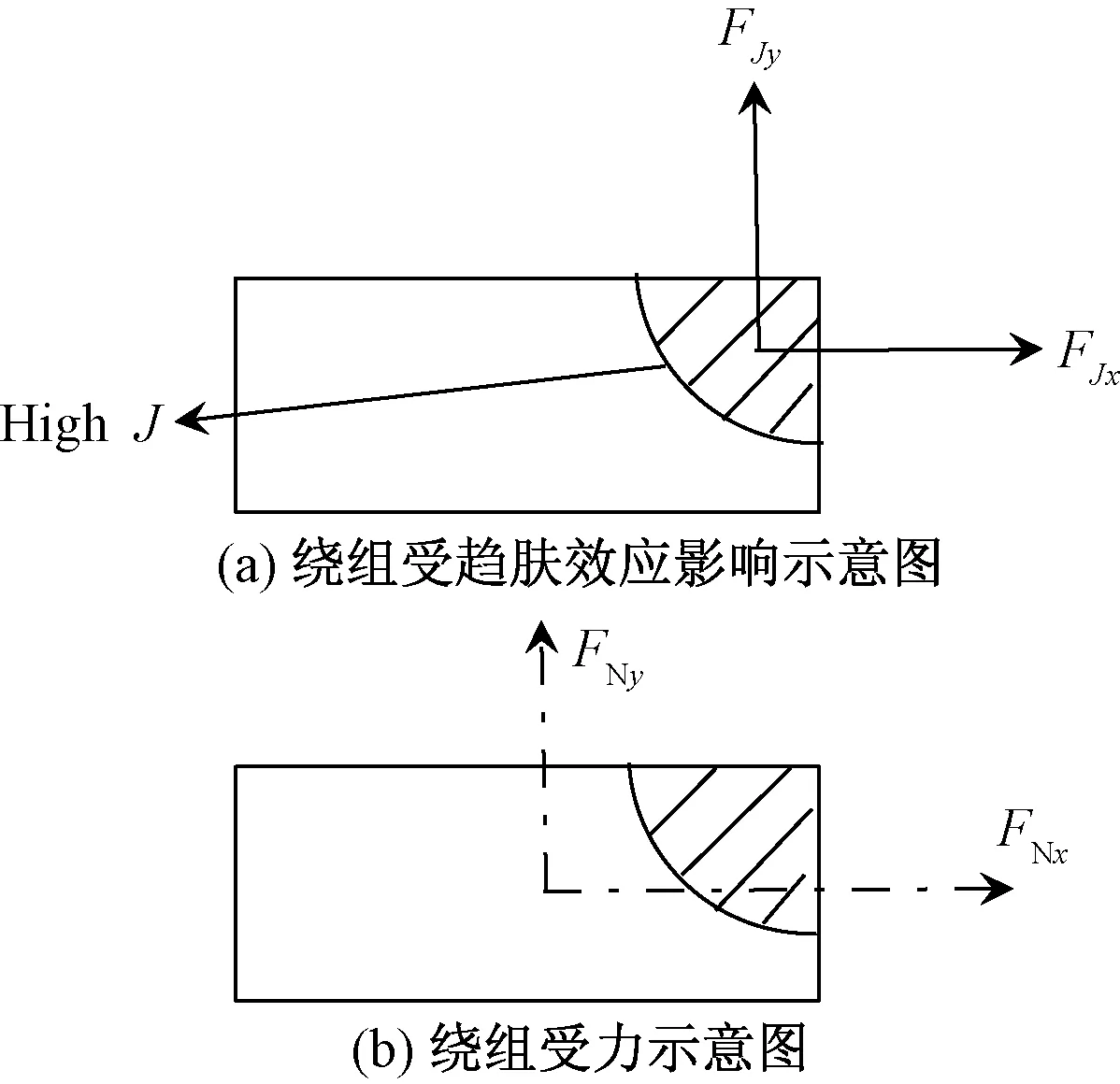
图4 绕组受力示意图Fig.4 Winding force diagram

可以看到，在阴影极小区域内，由于电流堆积，则相比于相同绕组的其他位置，该处电动力更大。因此直流偏磁导致的漏磁增大，相比正常情况下使得绕组更易发生单点疲劳以及绝缘损坏。

3 直流偏磁对变压器漏磁场的影响

以三相变压器中间相为例，绕组振动主要源于绕组中电流和漏磁场的相互作用，因此分析其振动特性，首先需分析直流偏磁下的漏磁场情况，考虑铁心硅钢片材料磁特性的非线性，建立磁路模型对其漏磁场进行分析，如图5所示[9-10]。

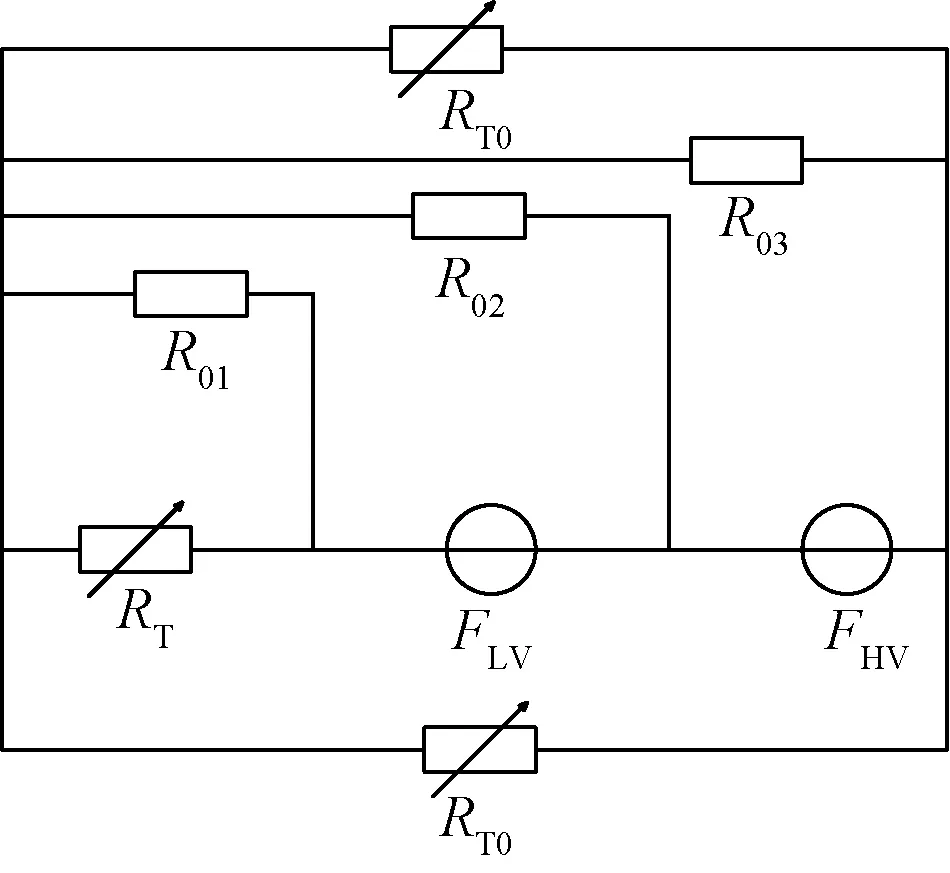
图5 磁路模型Fig.5 Magnetic circuit model

铁心中柱磁通的磁阻为RT。空气中漏磁通对应磁阻为R01、R02、R03。铁心旁柱中磁通对应磁阻为RT0、FLV和FHV分别表示低压绕组和高压绕组饱和后增长的磁动势。与电路原理相近，单独对高压磁动势列写方程为

(4)

通过式(4)可以看出，偏磁饱和后磁势FLV增加，相应的铁心磁阻RT和RT0增大。由于空气中的磁阻不变，因此通过铁心的漏磁φT0减小，相应的空气中的φ0i能够分到更多的磁密，漏磁增加，φ1、φ2、φ3迅速增大。多余磁密被挤到空气中，如图6所示为径向漏磁场计算结果图。

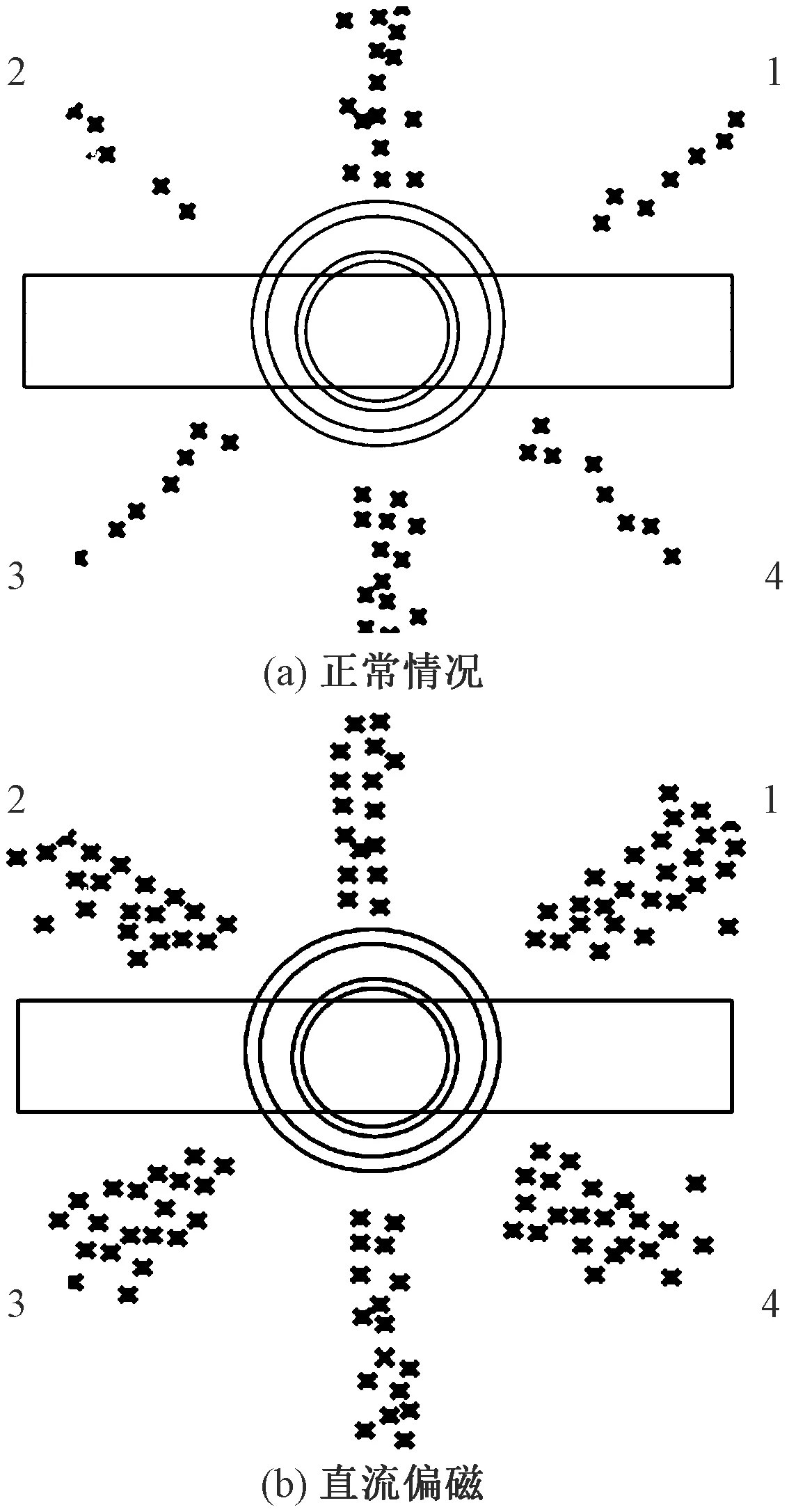
图6 直流偏磁下铁心漏磁分布Fig.6 Magnetic flux leakage distribution

可以看到，相比正常情况下，漏磁在20°和160°斜对角明显增加。需要注意的是被挤到空气中的磁密并非无序分布，而是紧贴铁心。斜对角轴向漏磁的增大以及电流波形的畸变必然导致绕组径向振动的增加以及振动位置变化。

4 绕组振动特性仿真分析

4.1 绕组及垫块振动特性

如图6所示，当发生直流偏磁时，变压器漏磁增加，轴向漏磁分布在20°和160°左右的斜对角线处。绕组振动模式发生变化，出现新的单边振动模式。如图7所示为直流偏磁下绕组垫块和线饼位移情况。即在图7所示斜对角处存在单边最大振动偏移现象，破坏了绕组原本振动对称的平衡性，且最大位移方向与分析的漏磁分布相符。可以注意到该处的垫块明显向外偏移，增大了垫块脱落的可能性，且对称方向的垫块存在着与绕组接触分离脱落的可能。

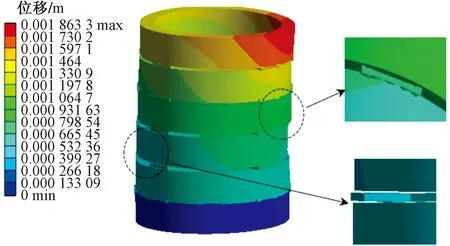
图7 直流偏磁下振动分析Fig.7 Vibration analysis under bias

相比正常情况下，直流偏磁时由于电流单边峰值上升，相应的振动最大点的位移峰值增加，绕组的单边振动将会加剧振动点处的绝缘破坏以及铜的疲劳老化，更易发生塑性形变，造成不可逆的损坏，当发生短路冲击时更使得该处更容易发生损坏。部分绝缘垫块的错位脱落位置与振动位置相符合，由于绕组不对称振动使得垫块脱落可能性大幅增加。部分垫块分离脱落位置与振动最大位置相对，其并非由于振动导致脱落，而是由于振动模式变化导致的振动不对称性使得绕组线饼和垫块受力不平衡而产生分离脱落现象，垫块脱落将使得短路发生概率增大。单边振动模式和垫块脱落将会使得变压器抗突发耐受能力下降。

4.2 趋肤效应和邻近效应的影响

同时绕组由于集肤效应和邻近效应的影响，电流会在绕组表面棱角处堆积，使得相同截面的绕组受力不均匀，如图8所示。

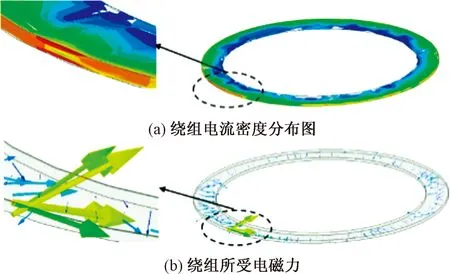
图8 直流偏磁下绕组趋肤效应影响分析Fig.8 Analysis of the effect of skin effect on winding under DC bias

在绕组上方单独建立单匝绕组模型来分析绕组内电流分布对于绕组受力的影响。可以看到，由于集肤效应和邻近效应的影响，电流的堆积使得绕组在边缘棱角极小的截面处受到较大的电动力。根据上文分析，单点突出的振动模式使得绕组单边振动加剧，疲劳增加，而集肤效应和邻近效应将使得这一现象更为突出。

综上所述，绕组单边振动模式和集肤效应、邻近效应使得铜和表面绝缘层疲劳加剧，且垫块脱落使得短路发生概率大幅增加，使得变压器抗突发能力大幅降低。

4.3 不同预紧力对绕组振动及垫块的影响

由于垫块是渐刚性材料，非线性使得其杨氏模量随着预紧力的增大，垫块刚度增加，因此可以通过改变垫块的杨氏模量来模拟预紧力的改变，及更高的杨氏模量与更大的预紧力两者等价[11]。如图9所示为直流偏磁下同一时刻，不同预紧力下绕组振动特性图，图中显示为垫块绕组线饼位移情况。

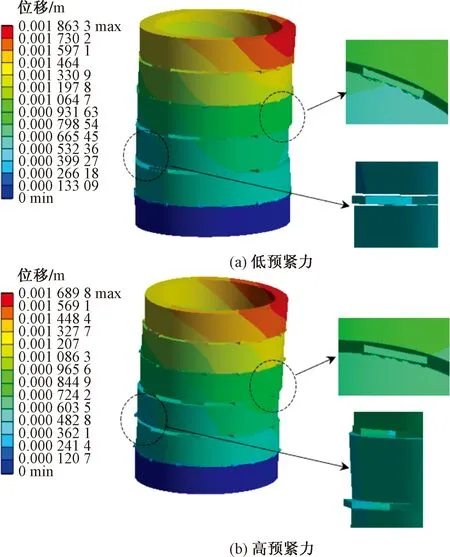
图9 不同预紧力下绕组振动特性Fig.9 Vibration characteristics of windings under preload

可以看到，随着绕组预紧力的增加，绕组整体位移更趋近于稳定，振动位移得到抑制。然而垫块的错位脱落以及相对位置的线饼和垫块分离现象虽稍有改善但是仍然存在，这是由于偏磁情况下的振动模式改变使得垫块受力不平衡产生，因此不会随着其他因素而改变。

5 振动实验

以一台实际运行中的220 kV变压器进行振动测量，如图10所示。因变压器直流通过接地中性点流入变压器故接地中性点中的测得的直流电流分量可以表征偏磁[12]。实验采取振动信号与中性点电流信号同步测量的方式，通过同一分析仪进行两种信号的同步采集，能够对于变压器多测量进行同步观测，对变压器状态进行更准确的判断。如图11所示为传感器布置位置，共8个测量点。

图10 变压器振动实验Fig.10 Transformer vibration experiment

由于实验中仅能利用压电式传感器布置在变压器箱体表面，因此为了与实验结果相契合，利用流固耦合多领域联合得到的油箱表面流体振动，如图12所示为油箱壁面压力分布图。可以看到，箱体表面压强分布与上述漏磁分析方向相一致，振动最大处位于箱体左右两侧，压强由两侧到中间逐渐减弱。

测得的中性点电流频谱图如图13所示，选取的测点1和测点2两点。可以看到，相比于正常情况下，直流偏磁时谐波特别是偶次谐波增长明显，尤其是以低次谐波为主。同时中性点电流中包含偶次谐波，说明此台变压器正运行于直流偏磁状态。

与电流测量时间保持同步，测得的振动波形和频谱图如图14和图15所示。可以看到基频处振动幅值几乎并未增加，谐波处振动明显增加，与电流变化保持一致，说明振动、电流双参数同步测量方法的有效性。

测得的振动波形如图15所示。可以看到1号测点和2号测点的振动时域图均发生偏移现象，且1号测点的振动明显大于2号测点位置，与前文图11的流体振动仿真分析结果相符，说明直流偏磁情况下振动的偏移和振动模式的不对称性。

图11 振动实验测点分布图Fig.11 Distribution map of vibration test points

图12 油箱表面振动分析Fig.12 Analysis of surface vibration of fuel tank

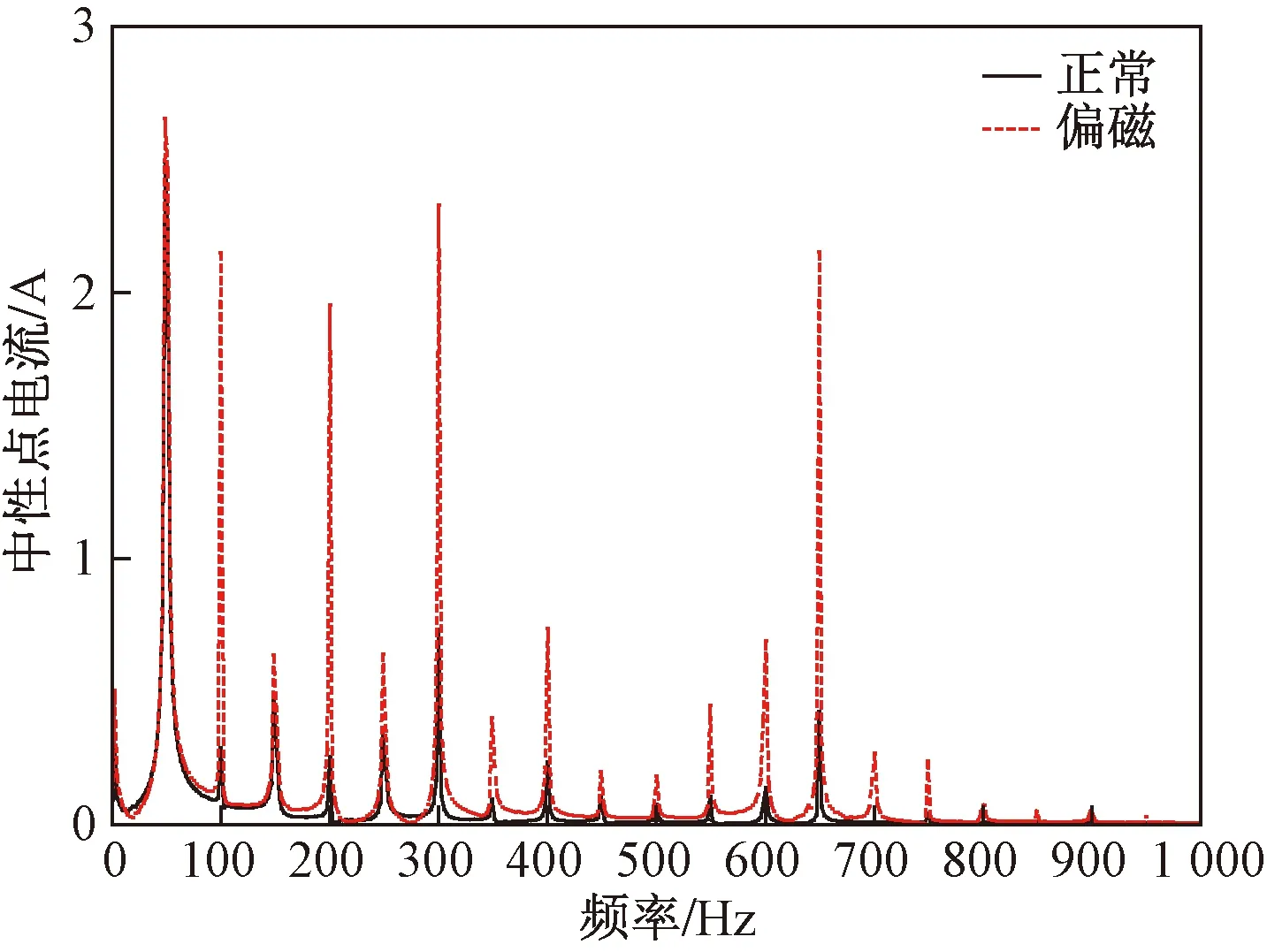
图13 中性点电流频谱图Fig.13 Neutral point current spectrum

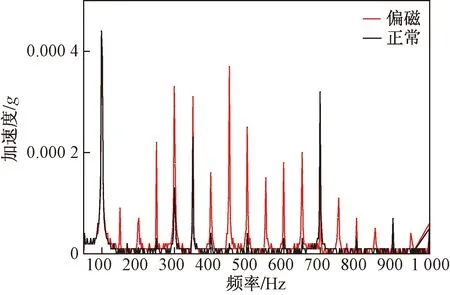
图14 振动频谱图Fig.14 Vibration spectrum

6 结论

建立包含垫块的线饼式绕组精细化模型，通过电磁场-结构场-流体场多物理场耦合的方法对变压器直流偏磁下绕组及垫块的振动位移特性进行分析，得到结论如下：

(1)漏磁在紧贴铁心的20°和160°斜对角处增大，并在对应位置出现新的单边振动模式。绕组特别是上半部分绕组将会向一边偏移，绕组受到的径向电磁力导致的位移整体处于不平衡状态，使得变压器耐受抗突发能力大幅降低。

(2)受到绕组整体位移不平衡影响，垫块整体特别是上半部垫块因受向心和离心摩擦力的时间不再一致因此向单边发生偏移，发生错位脱落的可能性大幅增加，垫块脱落使得变压器耐受冲击能力降低。

(3)选择较大刚度的绝缘垫块或者保持预紧力防止松动能够有效抑制绕组振动，但对于绕组单边振动模式造成的不平衡情况无明显改善。

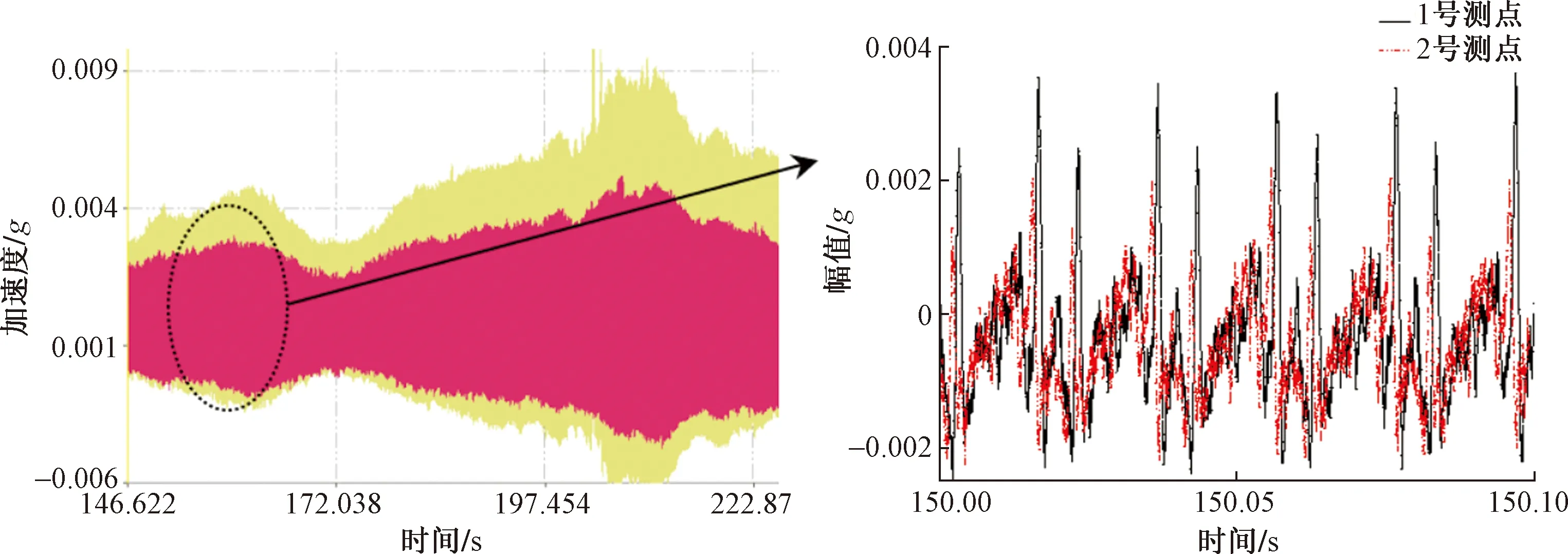
图15 时域振动结果Fig.15 Time domain vibration result