风电叶片疲劳共振加载方式参数分析及试验

周爱国，施金磊，乌建中

(同济大学机械与能源工程学院，上海 200082)

近年来，风电行业发展迅速，风电叶片是风电机组的重要组成部分之一，对于新型号的叶片，通常需要对其进行静力及疲劳加载测试以验证叶片的结构静强度和疲劳强度[1-2]。其中叶片的寿命很大程度上取决于其抗疲劳性能，因此叶片的疲劳加载试验至关重要[3-4]。早期对叶片的疲劳加载测试通常采用强制加载方式。美国国家可再生能源实验室(national renewable energy laboratory，NREL)于2004年研制了强制加载设备，通过液压执行机构施加强制力或控制位移方式使叶片的振幅达到设定值，进而完成疲劳振动测试[5]。虽然强制加载方式可操作性比较强，能够较为容易地实现试验要求，但该种加载方式的激振设备功率过高，能耗较大[6]。

针对强制加载耗能过大的劣势，共振加载方式应用逐渐广泛。目前常用的疲劳共振加载方式有旋转离心式和往复惯性式。这两种共振加载方式其实质都是利用质量块运动产生的惯性力激励叶片，且激振频率接近叶片的固有频率。Eder等[7]采用两个旋转离心激振设备实现对叶片的多点共振疲劳加载；Snowberg等[8]、Post等[9]采用液压往复惯性激振设备实现对叶片的共振加载；乐韵斐等[10]设计了电动往复式惯性加载设备，实现了对叶片的共振疲劳加载；同济大学相关研究团队也先后设计了旋转离心式及往复惯性式加载设备及配套的激振控制策略[11-13]。虽然这两种共振加载方式弥补了强制加载方式激振设备功率高、能耗大的不足，但在对叶片进行挥舞方向疲劳测试时，激振设备需要提供额外的力来克服运动质量块自身的重力，因此，激振设备也造成一部分的功率的消损。此外，激振设备的合理选型也是叶片疲劳测试的一大难点，激振设备功率过小，无法让叶片满足测试要求；激振设备功率过大，增加了测试费用，经济性较差。并且设备选型还依赖于测试人员的经验，这也增加了测试的准备时间。

针对常用共振加载方式的不足及激振设备选型困难等问题，现提出一种直驱式疲劳共振加载新方式，并对三种共振加载方式分别进行动力学建模和设备相关参数分析，建立三种设备所需电机功率与叶片自身共振功率之间的关系，并结合某型50 m叶片进行实例分析，得到三种加载方式下各激振设备所需电机参数，以验证直驱式加载方法的优越性，并为疲劳测试人员根据不同测试场景快速合理地选择激振设备提供理论依据。

1 叶片疲劳测试动力学模型

风电叶片具有变截面特征，叶片沿展长方向的力学性质存在差异性，为此可根据叶片各截面的刚度等参数将叶片离散化建模，由于所分析的是各加载方式激振设备的相关参数，因此可将叶片离散化振动模型等效为激振位置处的单点质量块-刚度-阻尼模型[14-15]，建立以叶根截面中心为原点的坐标系，平行地面且垂直叶片轴线为x坐标，相对于地面的垂直方向为y坐标，沿叶片轴线为z坐标，如图1所示。

EIi、li分别为叶片每段的抗弯刚度和长度；mi为叶片第i个离散点质量；Ff为作用在第f个离散点上的外部简谐激振力(i=1,2,…,f,…,k,…,n)图1 叶片加载系统等效模型Fig.1 Equivalent model of blade loading system

由于等效模型为非保守系统，可采用拉格朗日非保守系方程对图1中的等效模型建立动力学模型，拉格朗日方程的基本形式为

(1)

设M为叶片的等效质量，c为等效阻尼系数，k为等效刚度系数，根据上述参数可得到等效系统的动能、势能和耗散能分别为

(2)

取广义坐标qα=y，广义力Qα=F(t),并将式(2)代入拉格朗日方程可得到叶片单点激振等效动力学模型为

(3)

设外部简谐激振力F表达式为

F(t)=F0cos(ωt)

(4)

式(4)中：F0为激振力幅值；ω为共振圆频率。

根据式(3)和式(4)可得此二阶线性常系数非齐次微分方程的通解为

y(t)=Ye-ξωntsin(ωnt+φ)+Ycos(ωt+ρ)

(5)

式(5)等号右边第一项是有阻尼自由振动齐次方程通解，反映的是叶片振动的暂态过程，在分析稳态疲劳振动时可不予考虑；等号右边第二项是稳态强迫振动非齐次方程特解，叶片按激振频率ω作周期性等幅振动，因此叶片稳态振动响应为

y(t)=Ycos(ωt+ρ)

(6)

由式(3)和式(5)可得叶片振幅Y和相位差ρ为

(7)

由式(7)可知，当阻尼比ξ很小时，相位差ρ≈-π/2，即叶片激振点处位移落后激振力约π/2相位角。

由叶片稳态振动响应以及激振力的表达式，可求得叶片所必需的激振功率以及在一个周期T内激振能耗分别为

(8)

式(8)中：PF为叶片的共振功率；WF为叶片在一个振动周期内的能耗。

2 叶片疲劳测试方式

目前对叶片进行疲劳测试都是采用共振加载方式，共振加载原理是：对叶片施加简谐激振力，且激振频率接近叶片的固有频率，让叶片产生明显的振型。常用的共振加载方式有旋转离心式、往复惯性式和直驱式。三种共振加载方式所需激振设备不同，因此激振设备各参数也不同。结合叶片的受迫共振，可以进一步分析三种共振加载方式在对叶片进行疲劳测试时激振设备各自的工作参数。

2.1 旋转离心式共振加载方式

旋转离心式共振疲劳加载方式是利用安装在叶片夹具上的动力装置驱动偏心质量块旋转产生的离心力对风电叶片进行加载。叶片旋转质量离心式垂直疲劳加载装置由变频器、电机、减速机、偏心质量块等组成，如图2所示。

图2 旋转离心式共振加载测试方式Fig.2 Rotating centrifugal resonance fatigue test method

参照图1和图2可建立如图3所示的挥舞方向离心式加载系统动力学模型，离心式坐标系原点设在叶片静止时运动质量块旋转中心处。运动质量块初始位置在激振器的最下端，叶片初始位置为静力平衡位置。

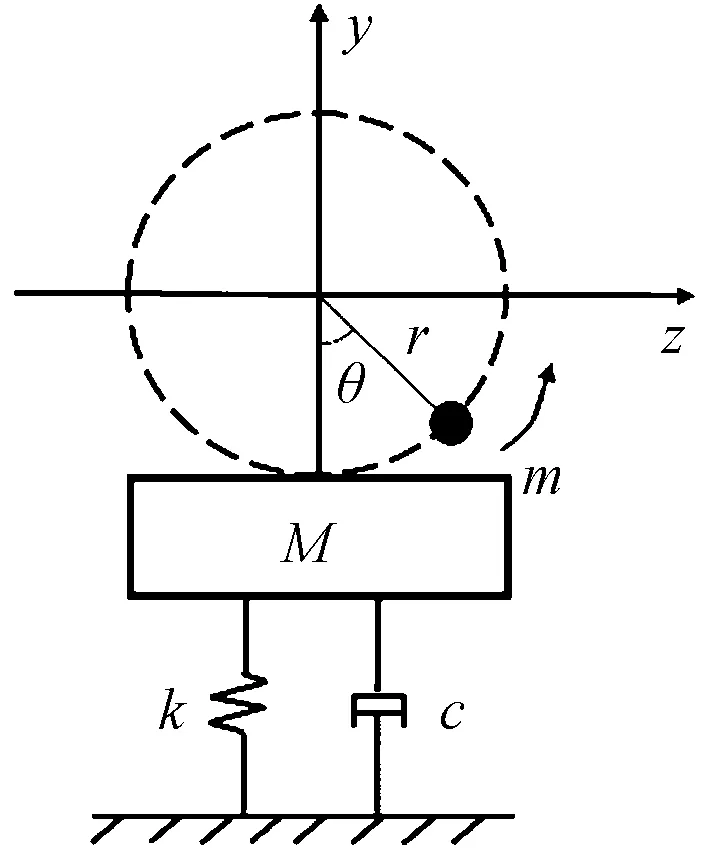
图3 离心式垂直激振加载模型Fig.3 Centrifugal vertical excitation model

设旋转质量块相对于叶片匀速运动，则可得旋转质量块在y和z方向上的相对于叶片运动方程Sy和Sz分别为

(9)

式(9)中：r为运动质量块旋转半径；θ为质量块旋转角度。

叶片在垂直加载过程中受到的激振力是由旋转质量块在y方向产生的离心力所提供的，因此叶片在y方向受到的激振力Fy为

(10)

式(10)中：m为运动质量块质量。

由式(6)和式(7)可得叶片在Fy激振力作用下响应为

y=-Ysin(ωt)

(11)

已知叶片和旋转质量块相对于叶片的运动方程后，可以分析旋转离心式激振器所提供的负载力，对旋转质量块进行受力分析，根据牛顿第二定律可以分别求得激振器在y和z方向上对旋转质量块提供的负载力Fload为

(12)

在旋转离心式加载方式中，其负载力矩Mload不仅与负载力有关，还与负载力作用的力臂大小有关，在t时刻，负载力产生的力矩Mload可表示为

(13)

式(13)中:My为在y方向负载力Fyload对x轴的力矩；Mz为在z方向上负载力Fzload对x轴的力矩。

旋转离心式加载系统配有减速机，则电机的相关参数分别为

(14)

式(14)中:i为减速比；MCen为反馈力矩；nCen为转速；PCen为瞬时功率。

当对叶片进行摆振方向的疲劳测试时，激振器参数满足式(12)和式(14)，但由于运动质量块自重方向与摆振方向正交，故激振器在摆振方向的负载力无须克服运动质量块自身重力，即式(12)中不包含质量块重力项。

2.2 往复惯性式共振加载方式

往复惯性式疲劳加载方式也是利用安装在叶片夹具上的动力装置驱动质量块在叶片加载方向做往复直线运动，利用运动质量块产生的惯性力使叶片往复振动进行疲劳加载。往复惯性式共振加载系统通常由液压作动器或伺服电机、滚珠丝杠构成。叶片电动伺服往复式疲劳加载装置如图4所示。将往复式挥舞方向共振加载系统简化成如图5所示的模型。

图4 往复式共振加载测试方式Fig.4 Reciprocating resonance fatigue test method

图5 往复式垂直激振加载模型Fig.5 Reciprocating vertical excitation model

与分析离心式加载模型相似，运动质量块作简谐运动，质量块相对于叶片的运动方程s、叶片受到惯性力F分别为

(15)

式(15)中:S为运动质量块行程。

由于往复惯性式加载方式与旋转离心式在y方向上施加的激振力形式相似，因此往复式加载系统中叶片的运动方程形式满足式(11)。

类似于分析旋转离心式旋转质量块的受力状态，由式(11)和式(15)可以分析往复式激振器所提供的负载力，对质量块进行受力分析，根据牛顿第二定律可以分别求得激振器提供的负载力Fload为

(16)

在往复式加载方式中，电机作用在丝杠上的负载力矩与电机轴上的反馈力矩相等。因此根据负载力矩、丝杠导程和轴力的关系，可以推导在任意时刻电机的相关参数为

(17)

式(17)中：MRec为往复式加载电机的反馈力矩；nRec为转速；PRec为瞬时功率；h为滚珠丝杠导程。

叶片在摆振方向疲劳加载时，往复式同离心式一样，无须克服运动质量块的自重，即式(16)不包含重力项。

2.3 直驱式共振加载方式

直驱式共振加载方式通过安装在固定装置上的执行机构产生的简谐激振力对风电叶片进行共振加载。直驱式共振加载方式可由伺服电机、缆绳和减速机构成，如图6所示。直驱式共振加载方式的激振器不安装于叶片上，故将其简化为如图7所示的模型。

与分析前两种加载模型相似，叶片受到的简谐激振力满足式(4)，且缆绳的运动形式与叶片运动形式一致，即满足式(11)。则激振器电机的相关参数为

图6 直驱式共振加载测试方式Fig.6 Direct-drive resonance fatigue test

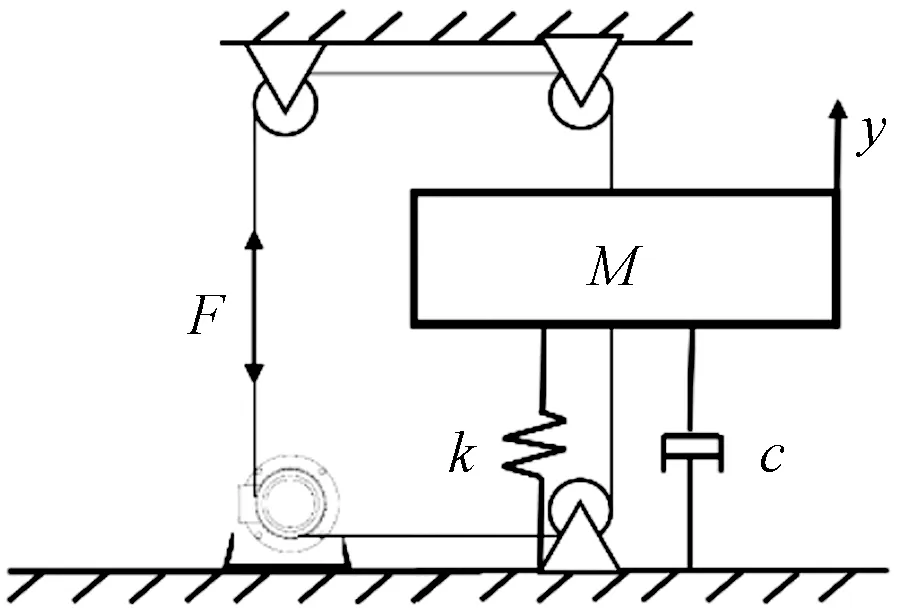
图7 直驱式垂直激振加载模型Fig.7 Direct-drive vertical excitation model

(18)

式(18)中：MDir为直驱式电机负载力矩；nDir为转速；PDir为瞬时功率；L为卷筒半径。

由于直驱式加载方式无须通过质量块的运动产生激振力，因此激振器在摆振方向的参数满足式(18)。

2.4 各加载方式设备参数对比

在叶片所需激振力幅值一定时，即F0=Fy=mω2r=mω2S，三种加载方式中电机提供的最大功率以及在一个振动周期内的能耗计算公式为

(19)

(20)

式(20)中：WCen、WRec、WDir分别为离心式、往复式和直驱式电机在一个振动周期T内的能耗。

根据式(19)和式(20)可以发现，相对于直驱式加载方式，惯性式加载方式由于间接通过运动质量块对叶片作用力，其所需要的最大功率以及能耗均比直驱式电机最大功率和能耗大。

综上所述，三种共振加载方式所需电机的相关参数解析式如表1所示，并且由式(8)和式(19)可建立三种加载方式的最大激振功率与叶片振动功率在垂直测试方向上的比值系数δi，以叶片振动功率为参考，可推出其余三种加载方式的最大激振功率，三者关系如表1所示。此外，三种加载方式激振器电机的反馈力矩和功率分别如图8和图9所示。

由表1中“功率比值系数δi”一栏可得到，当试验叶片确定时，其共振频率随之确定，则功率比值系数δi和激振点处叶片振幅呈反比关系。当激振器越靠近叶尖处，叶片振幅变大，电机克服质量块重力产生的额外功率变小，即功率比值系数减小。离心式和往复式电机最大功率接近，两种加载方式的功率比值系数接近为δi=1+g/ω2Y；而直驱式功率比值系数始终为1。因此，在结合具体叶片进行实例计算时，只需计算出叶片振动最大功率，便可根据功率比值系数求得各种共振加载方式所需的激振设备功率。三种加载方式电机的最大功率及能耗都不尽相同，这是因为惯性式加载方式中电机除了对叶片输入必需的功率和功，还要对运动质量块提供额外的功率和能耗，而直驱式中电机直接对叶片作用，无须输出额外的功耗。

3 实例分析激振器参数

以某型50 m叶片挥舞方向加载为例，所需的激振力两侧峰峰值为10 000 N，激振频率为0.479 Hz，激振位置为20 m处，激振处叶片振幅Y=0.405 m，离心式共振法中取质量块的旋转半径r=0.4 m，往复式共振法中取质量块运动的单侧行程为S=0.4 m，分别计算采用离心式、往复式和直驱式加载方式所需的电机输入功率、最大转速等相关参数，其中离心式、直驱式中减速器的传动比i=50，卷筒半径L=0.4 m,往复式共振法中滚珠丝杠的导程h=0.02 m。

表1 叶片垂直加载各方式电机参数Table 1 Motor parameters of each loading method in the vertical direction of the blade

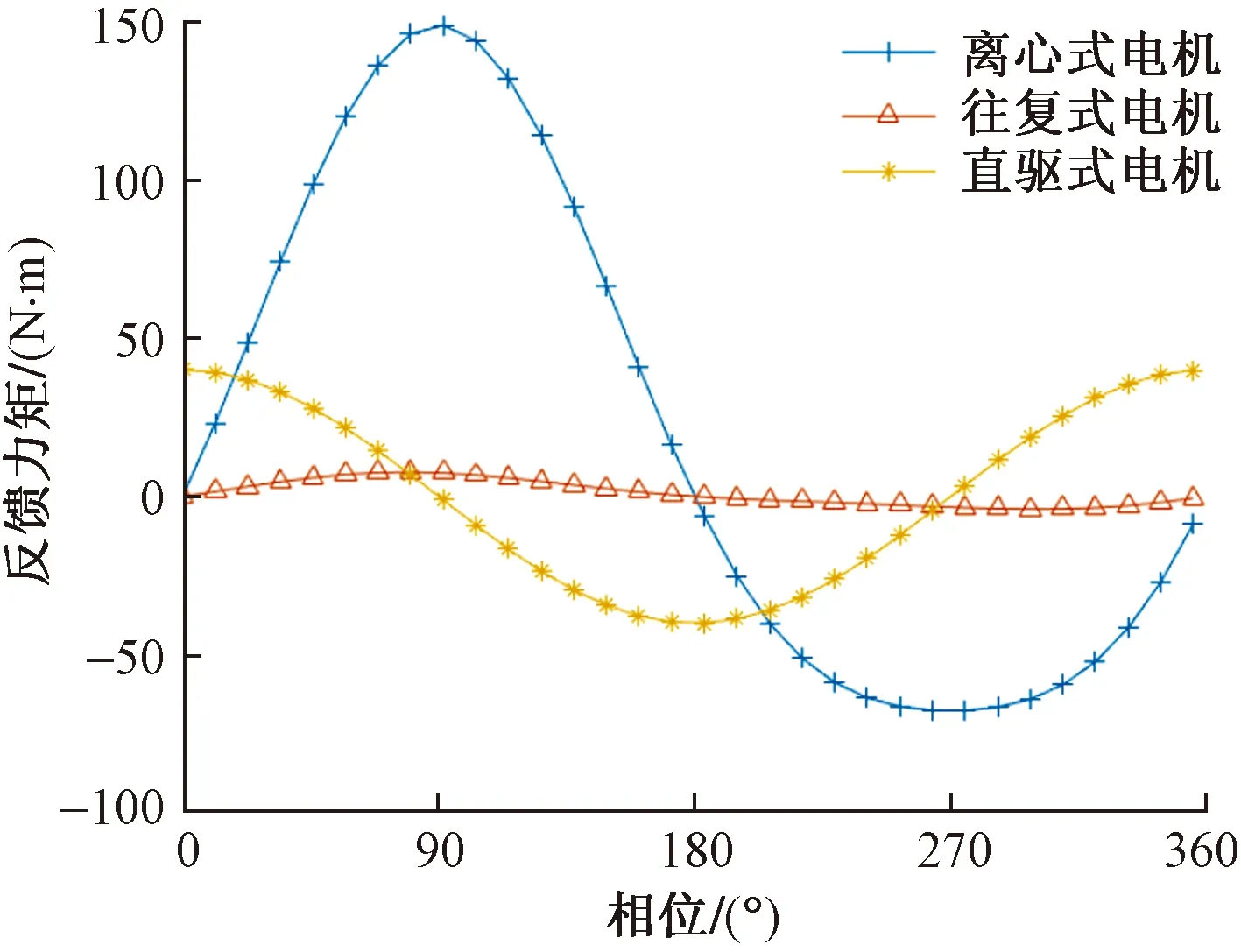
图8 激振器电机反馈力矩曲线Fig.8 Feedback torque curve of exciter motor

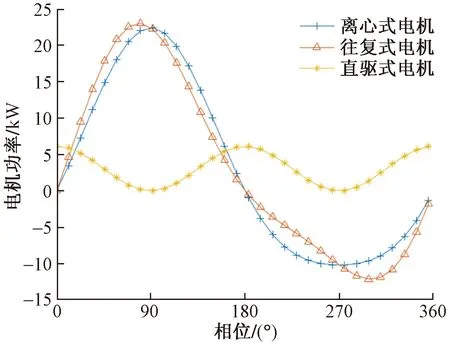
图9 激振器电机功率曲线Fig.9 Power curve of exciter motor

根据表1中的解析式以及功率比值系数求得三种共振加载方式激振设备所需参数，结果如表2所示。可知，在相同的激振条件下，三种共振加载方式激振设备所需功率各不相同，直驱式共振加载所需电机的最大功率最小，这是因为直驱式共振加载只需提供叶片所需的激振力，而离心式系统和往复式系统的激振器跟随叶片运动，在垂直方向加载时，激振设备除了为叶片提供所需的激振力之外，还需克服叶片对质量块的附加力以及质量块自身的重力。此外，离心式所需功率略小于往复式激振功率，是由于旋转离心式共振加载方式中其运动质量块在z方向上存在分运动，而往复式方式不存在分运动，且由式(13)和式(14)可知，在z方向和y方向对x轴的负载力矩方向相反，一部分负载力矩抵消，因此离心式所需总的负载力矩会略小于往复式的负载力矩，进而导致两者电机最大功率存在差异。通过功率比值系数可以快速地求得三种加载方式所需的电机功率，并且与解析解的最大误差小于2.7%。

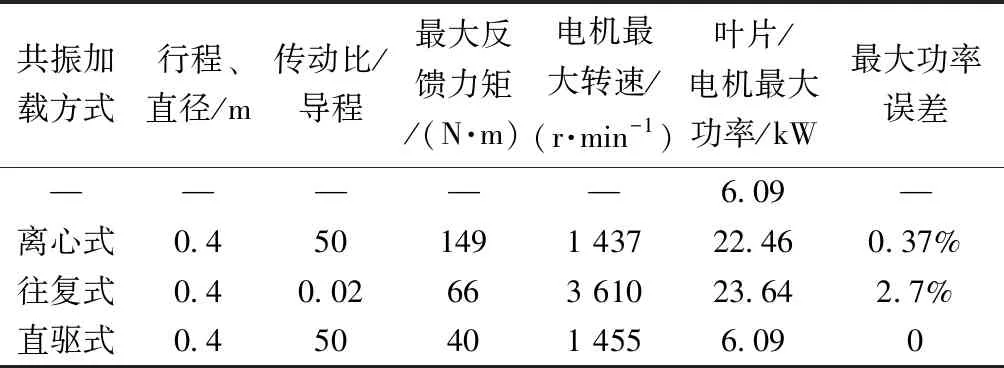
表2 三种共振加载方式实例结果Table 2 Results of three resonance loading methods

4 结论

针对离心式、往复式和直驱式三种叶片共振加载方式分析了其动力学模型并得到激振器所需参数的解析解，通过实例分析得出以下结论。

(1)建立了三种疲劳加载方式激振设备的参数解析式，通过叶片的固有参数和设计值便可快速确定激振设备的合理型号。

(2)建立了三种加载方式最大激振功率与叶片振动功率之间的关系，以功率比值系数δi表示，通过功率比值系数可以快速较准确估算电机所需的功率。当激振点作用于靠近叶尖处时，其振幅越大，离心式与往复式电机克服质量块自重产生的额外功率的占比越小。

(3)三种共振加载方式中直驱式共振加载方式激振功率最小，这是因为直驱式共振加载方式中负载力不用克服激振器运动质量块的自重，进而减小了总的输出功率。离心式共振加载所需电机功率比往复式共振加载电机的输出功率略小，这是因为离心式旋转质量块在沿着叶片展长方向存在分运动，总的负载力矩小于往复式电机的负载力矩，进而导致功率略小于往复式功率。

(4)直驱式激振设备所需功率及能耗最小，因此在进行叶片疲劳测试时，可优先选用直驱式疲劳加载方式。