频率域电磁法数值模拟进展

李长伟,高 磊,方小姣,刘 剑,万文武

(1.桂林理工大学地球科学学院，桂林541004;2.广西隐伏金属矿产勘查重点实验室，桂林 541004)

频率域电磁法是一种通过观测和分析由不同频率人工场源或天然场源激发的电磁场在地下介质中产生的感应二次场的分布规律，以获取地下电性分布特征和有关电性结构参数的地球物理勘探方法。包含主动源的频率域测深法(frequency domain sounding,FDS)、可控源音频大地电磁法(controlled source audio-frequency magnetotellurics,CSAMT)、海洋可控源电磁法(marine controllable source electromagnetic method,MCSEM)，被动源下的大地电磁法(magnetotelluric method under passive source,MT)、音频大地电磁法(audio frequency magnetotelluric method,AMT)和甚低频法(very low frequency method,VLF)等。根据趋肤效应的原理，频率域电磁法的探测深度随着频率的降低而增加，可对近地表以及深达地壳和上地幔的地球结构进行探测，在能源勘探、矿产普查、地壳和上地幔电性结构研究、海洋地质调查、地震预报、环境地球物理研究以及地质工程领域有着广泛的应用[1-2]。频率域电磁法的数值模拟对于理解复杂地质条件下的电磁响应特征，开发实用的数据解释处理软件，以及勘探方法的设计和仪器设备的开发等都有重要意义。频率域电磁法基于电磁感应原理，其数值模拟是采用各种数值方法对麦克斯韦方程组的合适形式进行求解。如基于电磁场满足的积分方程的形式、一阶微分方程形式、二阶微分方程的形式以及基于矢量和标量势的形式等。各种求解形式有着不同的优缺点，如基于二阶双旋度方程进行电磁场求解能够将电场和磁场解耦，可直接求得场矢量，但在求解电磁场时存在伪解问题，尤其在低频电磁场模拟时，由于离散双旋度算子奇异造成有限元方程近乎奇异而难以求解[3-4]，求解位势方程可实现电磁场的模拟从而避开伪解问题，但是需要进行数值微分求得场矢量。

近年来随着计算技术的快速发展，电磁法的三维模拟技术成为了研究热点，各种数值算法层出不穷，并在实际勘探中得到了广泛的应用。其发展趋势主要体现在：①采用各种数值技术提高模拟的精度和稳定性，如基于混合变分形式的混合有限元方法[5]、二维或三维电阻率反演成像研究的积分方程法[6]、提高插值精度的谱元法、通过自适应网格加密的自适应有限元方法[7-8]等；②提高对复杂模型的模拟能力，如介质各向异性情况下的模拟[9]、基于非结构化网格的模拟算法[10]等。

现基于不同模拟方法的分类，介绍频率域电磁法数值模拟技术的研究进展；介绍与电磁法模拟相关的大型线性方程组求解技术的进展；最后对频率域电磁法数值模拟技术的发展进行展望。

1 数值模拟方法的研究进展

目前，在频率域电磁法数值模拟中常见的数值方法包括积分方程法、有限差分法、有限单元法、谱元法、有限体积法等。下面分别对这几种常用的数值方法在频率域电磁法中的应用进行阐述。

1.1 积分方程法

积分方程法(integral equation method，IE)作为数值模拟算法中应用得最早的一种方法，是模拟三维问题的有效工具。IE的三维数值模拟过程通常是从麦克斯韦方程组出发，引入适当的并矢格林函数，将麦克斯韦方程组转化为第二类矢量弗雷德霍姆(Fredholm) 积分方程，将积分方程离散化为矩阵形式，求解矩阵方程组便可得到异常体内电磁场值，对异常体内电磁场进行数值积分，可求得空间内任一点的电磁场值。

从20世纪60年代开始，国外已经开展了三维电磁响应的数值模拟研究，Benbett等[11]首次在电磁学领域中采用积分方程法，Hohmann[12]第一次基于麦克斯韦方程组将积分方程法运用到三维大地电磁测深数值模拟研究当中。一直到20世纪90年代，随着计算机内存的增大及各种技术的迅猛发展，积分方程法实现了从均匀半空间单个异常体扩展到带地形的复杂介质的三维正演模拟，很多国外学者对积分方程算法提出了一系列改进[13]。到21世纪，积分方程法已基本成熟，美国犹他大学开发了一种基于积分方程法的三维电磁正演软件——INTEM3D，此软件可以对水平层状介质的三维复杂地电结构用积分方程法进行频率域电磁模拟。

在中国，许多学者对三维积分方程的研究也做了大量的工作。周熙襄等[14]对积分方程提出了一种近似解法，使计算速度大为提高，并讨论了任意三维地质体数值模拟的问题，计算结果精度较高；殷长春等[15]提出了将积分方程理论用于轴向频率域电磁测深三维正演；鲍光淑等[16]深入研究了均匀导电半空间频率三维电磁响应的数值模拟，将积分方程化为矩阵方程，计算出了空间中任意一点的电磁场分量；底青云等[6]从微分方程的积分解出发，推导出表达式极为简单的三维雅可比系数矩阵，构造了成像方程，合成了数据模型结果及实际资料的图像，这种方法实现起来极容易，成像结果的精度也相当高。随着IE的发展，为了提高数值模拟的计算速度，学者们还研究了各种近似求解方法，例如准解析近似解、Born近似解、扩展Born近似、准线性近似等。许诚等[17]在一个典型的矿区模型中采用积分方程准解析解法实现了极低频电磁法三维正演；任政勇等[18]提出了一种新的三维大地电磁积分方程正演技术，采用四面体网格技术离散异常体得到大地电磁积分方程，准确计算线性方程中的并矢格林函数的奇异积分，结合Pardiso高性能并行直接求解器，实现了三维大地电磁问题的高精度求解。

积分方程法的优点是只需要对异常体进行剖分，与微分方程相比，IE没有边界等复杂的问题，所以计算速度较快、内存占用少且物理意义明确。随着计算机技术的迅速发展，对异常体的数值求解变得更简单更快速，三维电磁响应数值模拟成为一种更廉价、更有效的解释技术。积分方程法的主要缺点是不适合复杂的三维地质模型的模拟。

1.2 有限差分法

有限差分方法(finite-deference method，FDM)是近似求解偏微方程边值问题常用的数值计算方法之一，该方法以差分原理为基础，将场域内连续的微分方程及边界条件用有限个离散的差分方程代替，进而把求微分边值问题转换成求解差分方程的问题。其过程为：首先将区域场离散化，用有限个网格的节点代替连续的求解域；其次将求解的未知数变量存储在各网格的节点上，并用差分代替微分，得到有限个未知变量的差分方程组；最后求解线性方程组得到电磁场的分布。

有限差分方法最早使用于电磁场数值计算是在20世纪60年代，Yee等[19]提出利用交错网格有限差分求解麦克斯韦方程组，奠定了电磁数值三维FDM正演模拟的基础(图1)，FDM成为模拟和解释复杂频率域电磁场的三维地质模型的重要方法之一[20]。Streich[21]提出了频率域可控源电磁数据的三维有限差分数值建模，对其进行直接求解和高精度优化；为了更好地模拟复杂介质模型和地形起伏情况，Weiss[22]采用非结构化网格FDM技术实现全球尺度的电磁三维正演，对局部加密的“Yin-Yang”网格进行改进，实现复杂介质的全球电磁三维正演；Mishra等[23]提出了一种新的无网格方法来模拟可控源大地电磁三维电磁响应，并利用径向基有限差分法(radial basis-finite difference，RBF-FD)对二维亥姆霍兹方程进行数值求解，得到了稳定的无网格方法。结果表明，该方法与标准的基于网格有限差分方法相比，在处理复杂模型上具有明显的优势。

在中国很早就开始利用有限差分开展地球物理中的模拟研究，唐大荣等[24]利用有限差分法计算出了大地电磁测深曲线，他们带领了国内并将有限差分法应用到地球物理模拟当中。进入21世纪，交错网格有限差分法得到了快速发展，该方法将磁(电)场定义在单元棱边的中点，将电(磁)场定义在单元表面的中心点，是一种有效的三维电磁正演模拟方法，使三维计算速度和精度得以提高。郭晨等[25]为系统考察多种复杂地层模型下的三分量感应测井的响应特征，从麦克斯韦电磁方程组出发，利用交错网格有限差分法推导三维频域电磁响应的差分计算公式。简而言之，频率域电磁法FDM三维正演模拟逐渐地从天然场源扩展到人工场源、从各向同性介质扩展到各向异性介质、从地面电磁扩展到海洋电磁和航空电磁等各个领域。傅磊等[26]为了研究频率域海底电磁法在油气勘探中的可行性,根据海底电磁法的观测特点,建立海底三维地电模型,采用频率域FDTD三维正演模拟程序,计算不同参数时频率域电磁响应,获得了不同模型、不同频率下电磁场的响应。佟拓[27]着重研究海洋人工源频率域电磁法三维正反演算法，建立较系统的海洋人工源频率域电磁法三维数值模拟、三维反演技术理论，为开展海洋人工源频率域电磁法的应用奠定基础。

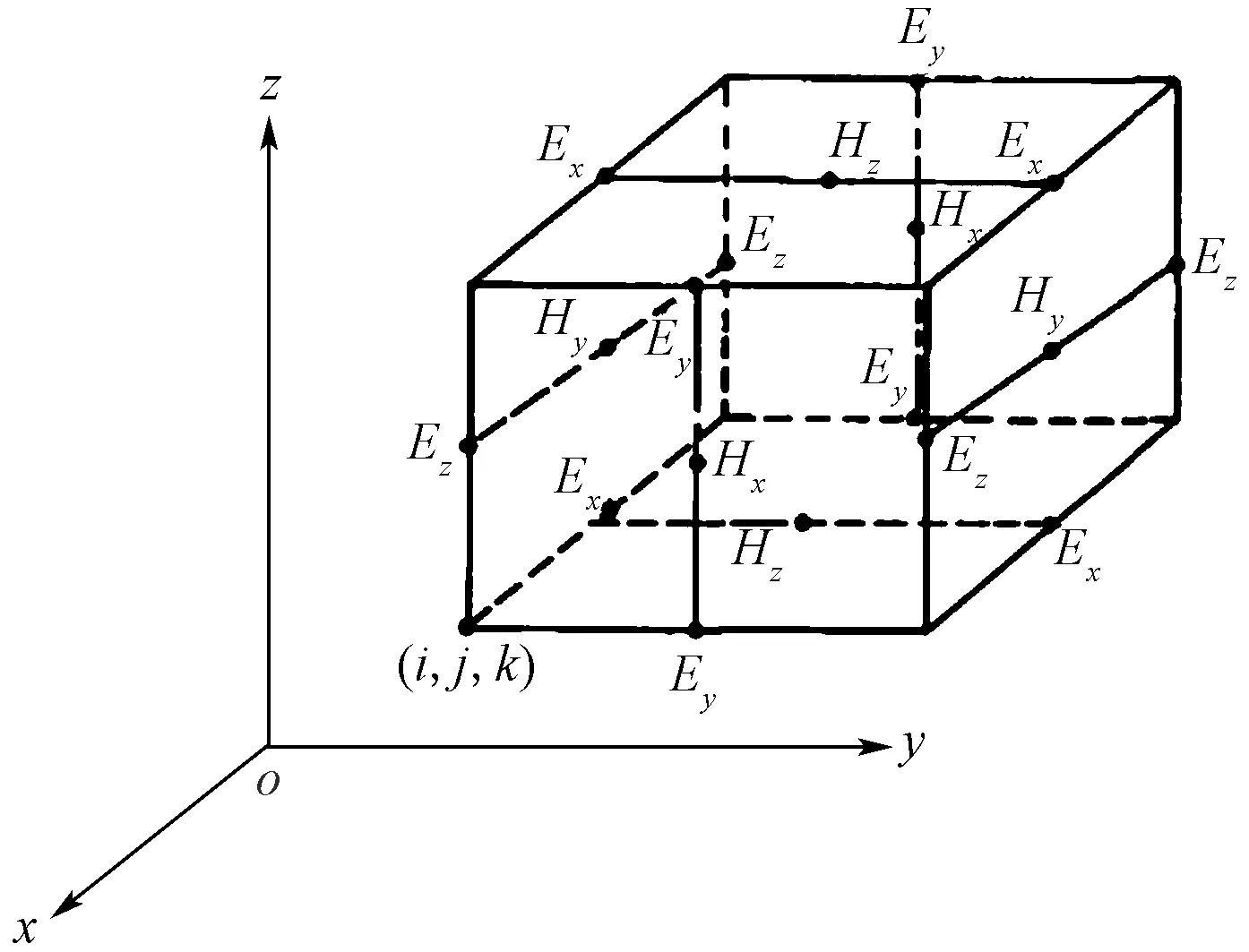
Ex、Ey、Ez为x、y、z方向的电场分量；Hx、Hy、Hz为x、y、z方向的磁场分量图1 有限差分Yee网格Fig.1 Finite difference Yee grid

有限差分法是一种直接将微分问题变为代数问题的近似数值解法，数学概念直观，表达简单，是发展较早且比较成熟的数值方法，该方法具有计算简单，运算速度快，迭代收敛也稳定的优点，特别是在介质模型形状规则简单，容易被剖分为单元四边形或六面体时，能够很好地解决内部介质中电磁差异引起的电场和磁场的不连续性,需要对整个区域进行网格离散；但是有限差分法不能基于非结构化网格剖分，不适合物性参数分布复杂且边界几何特征不规则模型的模拟。

1.3 有限元法

有限元方法(finite element method，FEM)是直接求解电磁场满足的微分方程，该方法以变分原理和分片插值为基础，通过变分导出相应的泛函，把求解域剖分为足够小的单元，在单元上对电磁场进行插值近似，并进行单元积分，再作计算区域内所有单元矩阵的组装合成，形成一个大型稀疏线性方程组，通过直接分解或迭代求解技术求解线性方程组可得到电磁场分布。

FEM最初是用于解决结构力学和应力分析的问题，直到20世纪70年代，Coggon[28]将其应用于电磁法领域，从电磁场能量最小原理出发，用有限元法实现了电磁场正演模拟。在三维频率域电磁法正演中，有限元法在处理复杂介质模型和起伏地形方面比较有优势，使得该方法在FEM模拟中得到了广泛的应用[29]。Badea等[30]进行了基于库伦规范的磁矢量势A和电标量势Φ(称为A-Φ方法)的三维各向异性介质可控源电磁的有限元正演模拟，常规的节点有限元不能满足界面上的连续性要求，需要强加散度条件来提高计算精度。近年来发展起来的矢量有限元把自由度取在单元的棱边上，能很好地满足电场的切向连续性，也能很好地施加边界条件，且一阶矢量有限元插值基函数自动满足散度为零的条件，相比节点有限元具有更大的优势，在电磁场模拟中得到越来越多的应用。Mukherjee等[31]和Silva等[32]使用矢量有限元法进行了三维标量CSAMT的正演模拟。

有限单元法在20世纪70年代末开始应用到电磁法数值领域中。近年来，中外对有限元的研究水平几乎相当。黄威等[33]对双旋度方程进行变分和离散后，采用压缩式储存总体刚度矩阵，采用直接分解法求解方程组，实现了三维矢量有限元法的航空电磁正演模拟计算；侯静等[34]提出基于有限元技术的传统木结构关键构造节点的性能研究与分析；为了易于模拟野外复杂地形和地下任意形状地电体模型，刘云等[35]推导出二维起伏地形条件下大地电磁法有限元数值模拟算法。王若等[36]用2D有限元正演来求取大地脉冲响应，实现多道瞬变电磁法的正演模拟研究。非结构自适应有限元方法能够解决复杂地电模型的数值计算问题，并可以根据计算误差自动地对网格进行细化，从而得到合理可靠的数值解。研究工作首先通过引入Cole-Cole模型，推导了在此模型下复电阻率二次场满足的边值问题;并利用有限单元法进行数值计算[37]。糜利栋等[38]提出基于有限元分析的页岩气扩散数值模拟。李长伟等[39]利用进行了电法测井的三维有限元模拟数值算例验证了方法的可靠性及计算效率,并对不同情形下的异常响应进行了分析,为进一步的反演工作奠定了基础。

有限元法的优点是求解过程规范，便于软件实现；内部边界条件互相抵消，成为本质边界条件，降低了边界处理的难度；可以采用非结构化网格剖分技术，适用于复杂形态异常体问题、多种介质和非均匀连续介质的问题，有较好的适应性和灵活性。但是有限元法也存在着不足，有限元方法离散后生成的是大型线性方程组，系数矩阵阶数很大，且常为病态矩阵，条件数很大，求解困难。

1.4 谱元法

谱元法是解偏微分方程的一种数值方法。其要点是把解近似地展开成光滑函数(一般是正交多项式)的有限级数展开式，即所谓解的近似谱展开式，再根据此展开式和原方程，求出展开式系数的方程组。对于非定常问题，方程组还同时间有关。谱方法实质上是标准的分离变量技术的一种推广。

谱元法(spectral element method,SEM)属于广义有限元法，是建立在波动方程的变分或弱形式理论基础上，求解偏微分方程的一种有效的数值计算方法，最早由Patera提出，并用于流体力学中[40]。随后，基于谱元法比较好的计算精度和它本身收敛的特性，中外一些学者便开始了一系列的研究。在计算地球物理领域里，谱元法在地震研究中得到很大的发展，Seriani等[41]率先将基于切比雪夫基函数的谱元法引入2D地震波场传播的模拟中，取得了很好的结果。随后，Komatitsch等[42]将基于勒让德基函数的谱元法引入3D地震波场传播的模拟中，对于介质物性剧化烈变的模型也能精确地模拟体波和面波的传播特性。Komatitsch等[43]在谱元模拟中逐步加入混合网格技术、最佳匹配层技术、区域分解技术、并行技术等，开发和维护了谱元法开源软件SPECFEM3D，同时在实际地震模拟中谱元法取得了很好的应用效果[44]。

王秀明等[45]引入基于预先条件下共扼梯度法的元到元算法，提高了谱元法的计算效率和精度。刘有山等[46]分别基于费克特节点和科恩节点实现了三角谱元法在地震正演模拟中的应用。魏亦文等[47]提出了谱元法波场模拟中的属性建模技术，并证明了单元属性和节点属性建模方式的有效性。谱元法也是计算电磁中应用较多的技术。Liu等[48]将混合谱元法应用到各向异性损耗开域波导分析中，其中基于棱边的矢量GLL多项式和基于节点的标量GLL多项式分别用于拟合电场横向和纵向分量，并在使用高斯积分求取质量矩阵时采用了质量集中技术[48]。该方法完全消除了伪特征值并具有谱精度。

谱元法结合了谱方法和有限元法的思想，其中谱方法是在整个求解域上通过正交高阶展开函数寻求区域内的解，理论上谱方法可以达到任意高精度且具有指数收敛性，但对于复杂求解域问题的求解有一定的困难;而有限元法将求解域划分成小单元，通过单元内的插值和单元之间的关系求取全局的近似解，具有很强的区域适应性。谱元法与有限元类似，将区域剖分为互不重叠的基本单元，在每个单元内进行谱展开，对未知量(如电磁场值)在配置点处利用正交插值多项式进行谱逼近，再借助伽辽金加权残差法形成单元矩阵，进而合成总体大型线性方程组，最后求解得到全局的近似解。在谱元法中，若正交多项式阶数选为N=1或N=2，则分别与传统线性插值和二次插值的有限元方法完全一致。因此，谱元法即进行了单元剖分又在单元内进行谱展开，具有和有限元法相当的良好几何区域适应性，以及和谱方法相当的高精度和收敛特性，是一种极具发展潜力的求解电磁勘探正演模拟问题的数值方法。

频域谱元法也是在分析波的传播方面的一种有限元方法，具有很高的精确度和计算效率，同时谱元法由于结合了有限元法处理比较复杂结构的几何灵活特性，还有伪谱方法的高精度、快速收敛的特殊性质，在当前已经成为进行大尺度、复杂地质结构模型数值模拟的重要工具。

1.5 有限体积法

有限体积法将计算区域划分为一系列不重复的控制体积，使每个网格点周围有一个控制体积(图2)，并将待解的微分方程对每一个控制体积进行积分，就可以得到一组离散方程。适于流体计算，可以应用于不规则网格，适于并行，但是精度基本上只能是二阶了。

有限体积法(finite volume method，FVM)又称为控制体积法，其基本思想是将求解区域剖分成一系列不交叉的控制体积单元，使得各个体积单元满足守恒原理，然后对控制方程在体积单元内进行体积分离散[49-52]。该算法是有限差分和有限单元法的一种中间产物：在规则网格剖分情况下，与有限差分法等价，在非结构网格下与有限单元法类似。Haber等[53]利用有限体积法求解耦合势方程实现电磁三维正演;随后又对考虑磁导率的电场方程进行求解。Haber等[54]利用八叉树网格和多重网格技术实现复杂介质模型的电磁三维有限体积快速正演，随后又实现二阶精度离散的八叉树网格三维正演;Novo等[55]利用有限体积法求解耦合势方程实现各向异性介质的电磁感应测井三维正演;Marchant等[56]实现电磁感应场激发的激电三维正演;Weiss[57]利用有限体积法求解Lorenz耦合势方程实现不同类型场源的电磁三维正演;Haber等[58]用多尺度网格剖分技术实现复杂地形的电磁三维正演;Caudillo等[59]利用局部加密技术实现频率电磁快速、高精度的有限体积三维正演。

近十年，频率域电磁有限体积三维正演才开始逐渐在中国发展起来，也取得较大进展。王宁等[60]在非结构化网格的基础上采用有限体积法开发了二维大地电磁各向异性正演模拟的新算法。杨波等[61]利用有限体积法求解电场方程实现海洋电磁海底地形起伏的三维正演;张烨等[62]利用有限体积法求解Coulomb耦合势方程实现各向异性介质下的感应测井三维正演;周建美[63]利用有限体积法求解Coulomb耦合势方程实现各向异性介质下的海洋电磁三维正演;韩波等[64]实现不同场源形态下的海洋电磁法三维有限体积正演，并随后利用并行求解库进行加速;陈辉等[65]利用有限体积求解Lorenz耦合势对称方程实现不同类型场源的地面频率域电磁三维正演;彭荣华等[66]利用拟态有限体积法实现频率域CSAMT三维正演。赵宁等[67]对频率域可控源进行了三维正反演研究，其中正演采用了基于库伦规范条件的耦合势有限体积算法进行计算。周建美等[68]利用三维拟态有限体积法对双轴各向异性介质中回线源瞬变电磁响应进行了模拟计算。

有限体积法是20世纪六七十年代逐步发展起来的一种主要用于求解流体流动和传热问题的数值计算方法。基于Yee氏交错网格的有限体积法，对麦克斯韦方程在各个单元上的积分进行离散处理，能有效降低方程的微分阶数，同时也减少了地层电导率不连续对离散结果的影响，在电磁场数值模拟中得到了较广泛应用。有一些离散方法，例如有限差分法，仅当网格极其细密时，离散方程才满足积分守恒;而有限体积法即使在粗网格情况下，也显示出准确的积分守恒。

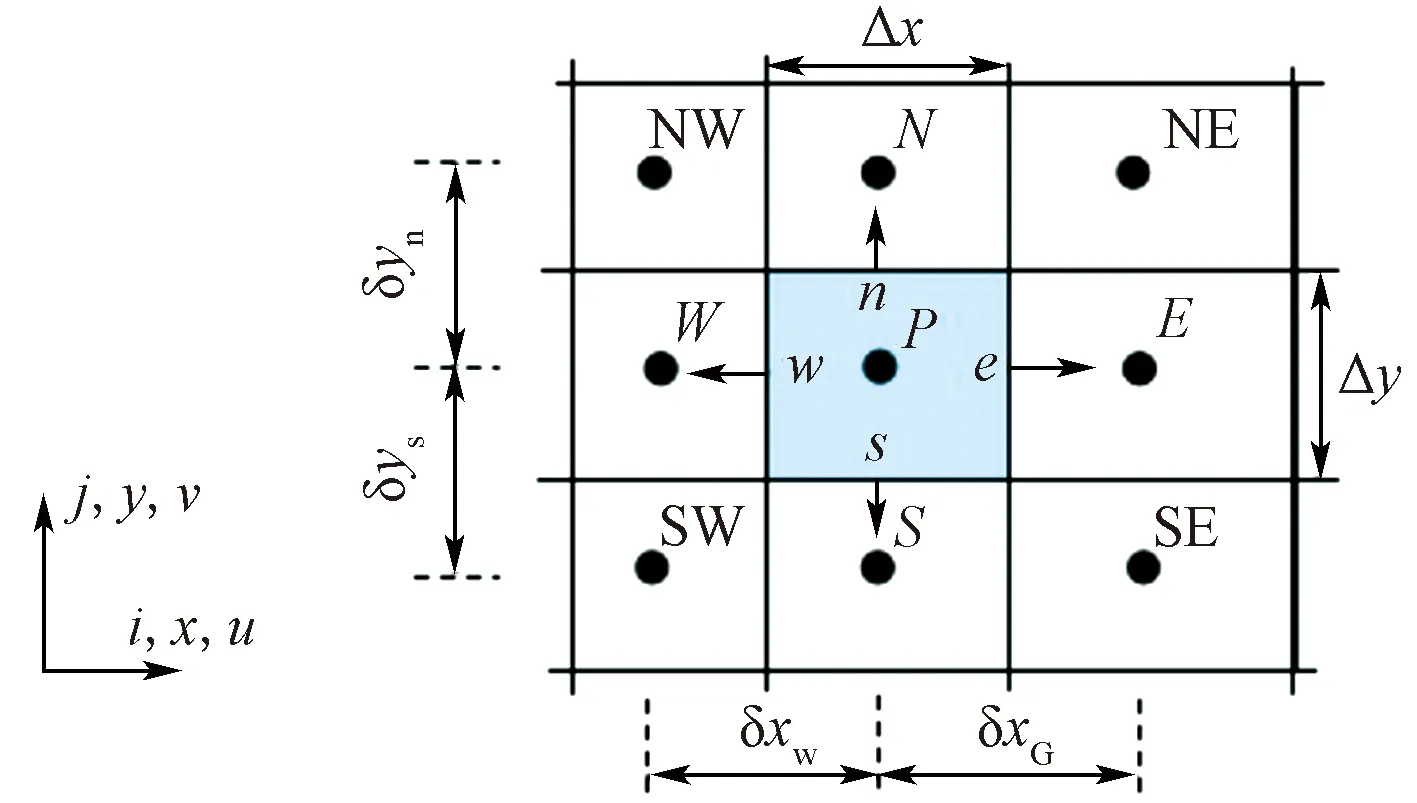
N、S、W、E、n、s、w、e分别为节点P所在的控制体积的单元界面;Δx和Δy 为WE方向和NE方向的间隔距离；δxW、δxG、δyS、δyn分别为各方向节点之间的步长图2 有限体积二维离散网格图Fig.2 Finite volume two-dimensional discrete grid diagram

2 线性方程组的求解技术

在电磁法正演计算过程中，首先是对其建立的数值模型进行网格剖分，其次对Maxwell方程组进行离散化处理，结合设定的边界条件，组成一个大型的稀疏性线方程组，最后求解该方程组得到地电磁响应。所以，如何高效、稳定且准确地建立三维数值模型并求解线性方程组，成为数值模拟中的主要问题之一。

三维电磁模拟生成的有限元线性方程组通常条件数较大，迭代求解收敛速度慢。采用基于LU分解的直接求解器在电磁场三维模拟中被广泛采用。直接求解器结合并行计算，则可进一步提高求解效率，如Pardiso、MUMPS等。Schwarzbach等[69]实现了在其高阶FE算法中使用Pardiso求解器解线性方程组，Grayver 提出一种采用非结构化六面体有限元法，结合MUMPS直接求解器求解线性方程组，实现三维电磁建模[70]；韩波等[71]使用并行化直接解法来求解离散线性系统，即对系数矩阵进行完全LU分解，通过调用大规模并行矩阵直接求解器(MUMPS)来实现，证明了直接解法的高精度性和稳定性；Puzyrev等[72]对各种直接求解数值方法在地球物理电磁正演中的应用效果和计算效率进行了系统性的分析[72]。

基于LU分解的直接求解器在矩阵分解过程中破坏了大型方程组系数矩阵的稀疏性，导致了求解器对内存的需求大大提高，这对于大规模三维问题的正反演求解而言具有很大的挑战，因此迭代求解方法在电磁法数值模拟中被广泛采用[73]。迭代求解器的弊端是经过几十次迭代之后，其性能就会下降。为解决这个问题，可根据频率域电磁法的系数矩阵方程的特征采用预处理方法降低矩阵的条件数，通过适当的预处理器加速Krylov子空间迭代方法[如双共轭梯度法(BICG)、双共轭稳定梯度法(BICGSTAB)；准残量最小化法(QMR)；最小残量法(MRM、Lanczos法)等]收敛。任政勇等[74]提出建立一个独特的电场强度-电场标量式(E-φ)联合系统，在求取得精确地电场E的情况下，BICGSTAB 迭代法可以有效地求解E-φ联合系统，为求解大规模地电磁感应数据计算奠定了基础。

一般的数值迭代方法对求解三维问题的大型稀疏线性方程组效率较低。多尺度计算方法的收敛速度与网格节点数及网格尺度大小无关，具有收敛速度快和计算工作量少等优点，其基本思想是用细网格光滑松弛将误差中的低频成分通过网格变换到粗网格上进行快速迭代消除，克服了一般数值迭代算法对于低频误差消除较慢的缺点，成为迭代求解大规模电磁问题的有效方法之一[75-76]。

3 结论

频率域电磁法的数值模拟技术近年来得到了快速的发展，三维的数值模拟已经实现，但是作为实用性反演解释软件的基础，其对复杂模型的模拟能力以及计算速度和精度需要进一步提高。

三维数值模拟大大增加了求解问题的规模，计算速度和内存需求是反演中需要解决的一个关键问题，制约了三维反演的有效应用，提升性能的方式之一是利用数值计算技术的发展，采用更优化的算法。另一种方式是采用更高性能的处理器，单纯依赖硬件升级来提高计算效率，但由于物理材料等的限制，短时间内单处理器的性能不会有大的突破。第三种方式是利用多个处理器资源或多台电脑，发展并行算法，对现有代码进行并行优化。目前计算机中主流处理器是拥有2～8个核心的多核CPU，及拥有数十乃至上百个核心的众核GPU，而且两者的核心数量仍会继续增加。多核和众核处理器的普及使得并行处理不再是大型机和集群的专利，这样必须由集群处理的任务，可以由PC 机来完成,特别适合野外勘探时进行数据资料解释。

实用的电磁法数值模拟软件应能处理包含起伏地形，介质各向异性，以及物性变化剧烈等各种复杂模型的模拟，采用无网格方法，非结构化网格、节点有限元、间断有限元方法，自适应有限元方法，谱元法等可以对复杂模型模拟的同时保持计算精度。而航空电磁和海洋电磁作为地球物理勘探技术未来发展的热点，对数值模拟的精度要求越来越高，在运用非结构有限元处理网格会应用的越来越广泛。网格边界运用有限元技术，与谱元法进行耦合，提高数值模拟的精度也将被更多的学者运用在研究中。在复杂介质下进行全频带电磁场模拟，采用多尺度的算法在不同尺度上离散，并通过不同尺度间的耦合可以有效地提高计算速度和精度，如多重网格方法，小波数值均匀化方法，多尺度有限元方法，多尺度有限体积方法等。这些数值模拟的技术发展将会进一步提高频率域电磁模拟的应用水平。