以“三会”为路径培育数学核心素养*
——以高三复习“导数的综合应用”为例
2021-02-25广东省广州市第六中学510300吴林
广东省广州市第六中学(510300)吴林
《普通高中数学课程标准(2017年版)》指出:“数学教育承载着落实立德树人根本任务、发展素质教育的功能.……提升学生的数学素养,引导学生会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界”,人们将其简称为“三会”.高中数学课程标准修订组组长史宁中教授指出:在本质上,这“三会”就是高中阶段的数学核心素养,是超越具体数学内容的教学目标.数学的眼光是什么呢?就是数学抽象.数学的思维是什么呢?就是逻辑推理.数学的语言是什么呢?就是数学模型.[1]
“三会”不仅表现为“结果”,也表现为“过程”.“三会”就是学习者面对情境中的问题,从数学的角度去分析和思考,直至找到比较满意的问题解决结果,其本质就是分析问题和解决问题的过程.[2]导数是研究函数的单调性、极值(最值)、图象和零点等性质最有效的工具,近几年高考中用导数研究函数性质的试题常常作为压轴题出现,对导数应用的考查颇为突出.本文以高三复习内容“导数的综合应用”为例,探讨如何依据“三会”来设计和实施教学主要环节,和学生一起寻找解题方法和策略.
人民教育出版社普通高中教科书《数学(必修第一册)》对函数零点的定义如下:对于一般函数y=f(x),我们把使f(x)=0 的实数x叫做函数y=f(x)的零点.这样,函数y=f(x)的零点就是方程f(x)=0 的实数解,也就是函数y=f(x)的图象与x轴的公共点的横坐标.所以方程f(x)=0 有实数解意味着函数y=f(x)有零点,而函数y=f(x)有零点意味着函数y=f(x)的图象与x轴有公共点.
以“数学的眼光”来看函数的零点求解问题,应该有两个策略:方程的角度——求解方程;函数的角度——函数的图象与x轴的公共点的横坐标,或者通过方程等价变形得到的对应的两个函数图象交点的横坐标.而研究哪两个函数的图象又是一个“用数学思维思考”的过程,对方程每一种等价变形都可以得到两个函数,通过研究两个函数图象的交点来研究原函数的零点,也就是我们俗称的“构造函数法”.通过研究和解决这类问题,按照“三会”来设计和实施教学,能很好地培养学生数学抽象、直观想像、逻辑推理和数学建模的核心素养.

用数学的思维思考 策略一中将原问题转化为两个函数的交点问题,是通过方程的等价变形实现的,最终是研究我们常见的函数.事实上,通过方程的恒等变形可以变换出无穷多对函数,我们需要引导学生思考:如何选择研究对象?转化的目的是让问题变简单,等价变形得到的函数应该是我们熟悉的函数或易于研究的函数,这也是转化思想的重要体现.
高三复习导数的综合应用时,我们需要特别关注培养学生“会用数学的眼光看世界”,即数学抽象和直观想像.以三次函数f(x)=ax3+bx2+cx+d(a>0)图象和性质为例,其导函数f′(x)=3ax2+2bx+c(a >0)为二次函数,二次函数的性质是学生们熟知的,两者的关系如下表:
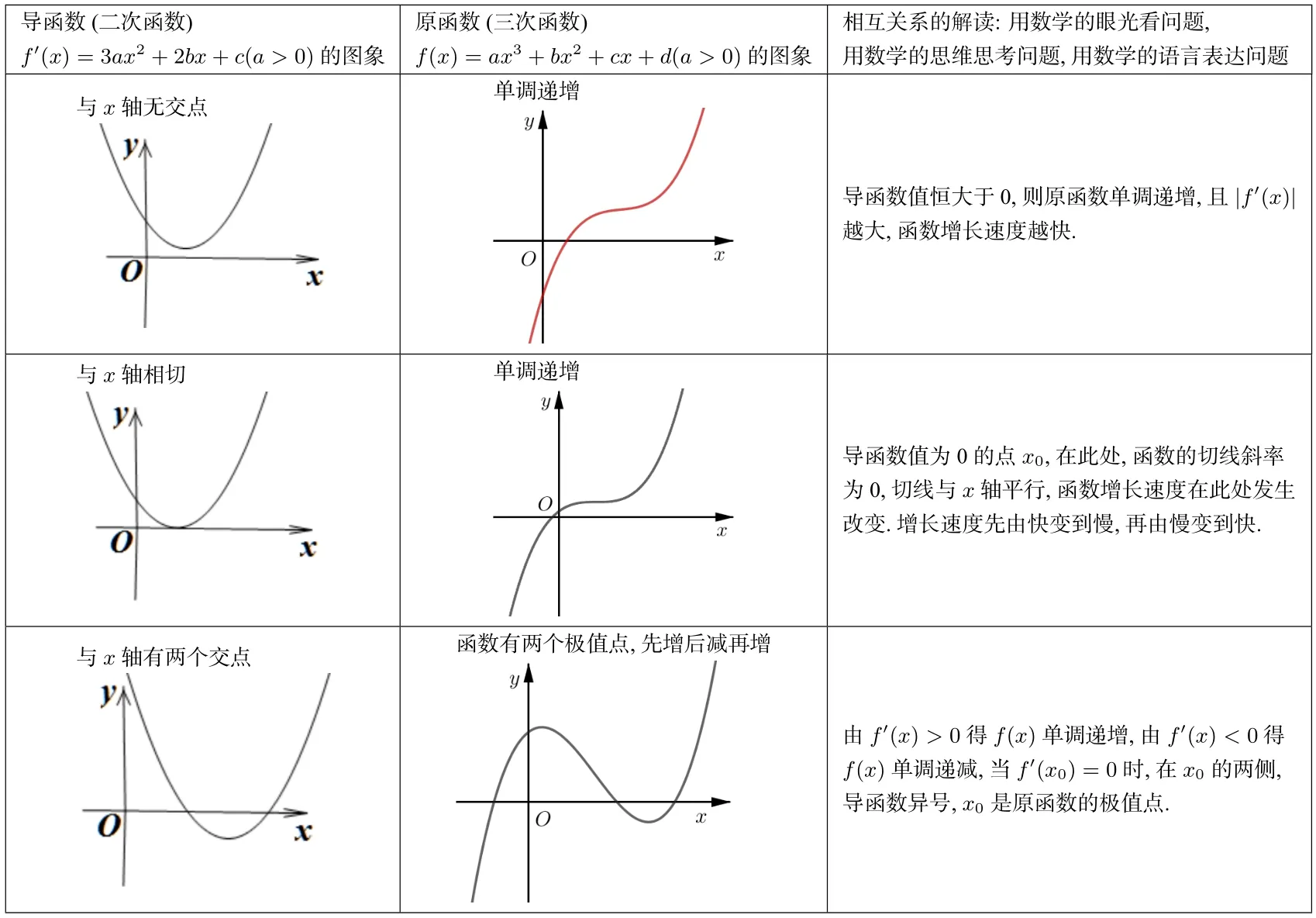
导函数(二次函数)f′(x)=3ax2+2bx+c(a>0)的图象原函数(三次函数)f(x)=ax3+bx2+cx+d(a>0)的图象相互关系的解读:用数学的眼光看问题,用数学的思维思考问题,用数学的语言表达问题与x 轴无交点images/BZ_41_500_1044_829_1307.png单调递增images/BZ_41_1039_1025_1350_1328.png导函数值恒大于0,则原函数单调递增,且|f′(x)|越大,函数增长速度越快.与x 轴相切images/BZ_41_500_1390_828_1675.png单调递增images/BZ_41_1039_1386_1351_1679.png导函数值为0 的点x0,在此处,函数的切线斜率为0,切线与x 轴平行,函数增长速度在此处发生改变.增长速度先由快变到慢,再由慢变到快.与x 轴有两个交点images/BZ_41_500_1754_829_2031.png函数有两个极值点,先增后减再增images/BZ_41_990_1737_1347_2048.png由f′(x)>0 得f(x)单调递增,由f′(x)<0 得f(x)单调递减,当f′(x0)=0 时,在x0 的两侧,导函数异号,x0 是原函数的极值点.
通过三次函数的实例,再次梳理导函数和原函数的关系,从实例中抽象出一般化结论,找到事物之间的相互联系,通过图象和文字语言表达两者的内在关系,并将这个研究结果建立成一般数学模型,用于研究类似的问题.通过这些策略能培养学生数学抽象、直观想象、逻辑推理和数学建模的核心素养,让学生会用数学的眼光看问题、用数学的思维思考问题、用数学的语言表达问题.
题目2(2021年高考全国II 卷第22 题)已知函数f(x)=(x−1)ex−ax2+b.
(1)略;
(2)从下面两个条件中选一个,证明:f(x)只有一个零点.①②.
用数学的眼光看 这是一个函数零点问题,可以直接研究函数图象,观察图象与x轴交点,若要画函数图象,需要先通过导数研究其单调性、极值和最值.“用数学思维思考”,导数f′(x)=x(ex−2a),通过定性分析和直观想像,学生能画出草图如右:
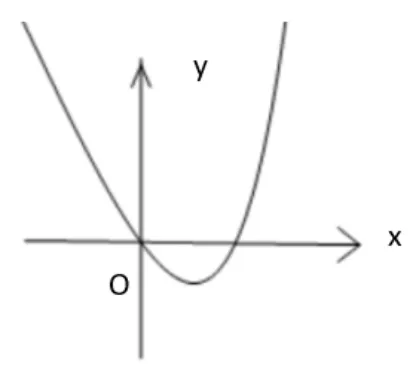
用数学的思维思考 引导学生类比三次函数模型,不难得出原函数先增后减再增,又x →−∞时,f(x)→−∞,又x →+∞时,f(x)→+∞,所以只需证明函数的极大值小于0(对应条件②),或函数的极小值大于0(对应条件①)即可.“用数学语言”函数极值与0 的关系来表达,使问题得到解决.
在用导数研究不等式、函数最值等问题时,我们可以把“三会”作为目标和路径,以数学知识为载体,自觉地利用数学抽象、逻辑推理、数学建模等最基本的思维方式和思维活动,去分析问题和解决问题.[3]
题目3(2021 高考乙卷第20 题)设函数f(x)=ln(a−x),已知x=0 是函数y=xf(x)的极值点.
(1)求a;
进一步,用数学的思维思考,换元t=1−x,可以使原式更简,换元得“即证tlnt−t+1>0 在t ∈(0,1)和t ∈(1,+∞)恒成立”.以下以“数学的语言”——函数的最值来表达,则问题归结为:证明函数h(t)=tlnt−t+1 最小值大于0,细节从略.
反思启示导数解答题题目众多,考查内容广泛,但若认真梳理近几年的全国高考题,会发现无论怎么变化,本质是用导数研究函数的单调性、极值、最值、图象和零点.在教学中,我们应立足“三会”,以“三会”为目标,同时,应以“三会”为教学设计的路径,教学生“看”——数学抽象、直观想像,教学生“思”——逻辑推理,教学生“表达”——数学建模,对每一个内容都立足于教材和学生的认知,明确研究内容在“三会”中的具体内涵与做法,使学生从旧知识中生长出新知识,从旧方法中生长出新方法,探究问题逐层递进、螺旋上升,从而培养学生的核心素养.
