关于解三角形平面图形类问题的策略研究——一道2021年高考题引发的思考

广东省东莞实验中学(523120)吴徐安娜

2021年高考已经落下帷幕,全国I 卷第19 题考察的是解三角形平面图形类问题,考完后学生哀嚎一片,可见此类问题是高考中的重点更是难点.笔者翻阅了许多文献,鲜有对这类问题归纳总结给出通法的.故本文将对此类问题作出总结,希望对各位有所帮助.

1 三角形中线模型

评注本题很多同学能够顺利的写到(∗)式,但是(∗)式后面的就无从下手,很多同学体会不到消元的思想方法,找不到认为两个方程,三个未知数就是无解,导致算不到最后结果.所以说除了总结模型和通法,学生的数学运算核心素养也亟需加强.

2 平面四边形模型

一般解三角形问题如果给出的平面图形是四边形,那么这其中所包含的三角形就有很多.笔者认为思考过程大致可以概况如下流程:设角→在某个三角形中由正弦定理用角表示边→在另一个三角形中用正弦定理或余弦定理找到等量关系→得出结论.

当然,如果题目众多三角形中有特殊三角形,比如直角三角形或等腰三角形,我们优先选择从这些三角形中设角.很多时候,学生没办法从一个三角形中找到等量关系,则尽可能多求图中的角.从而可以在两个三角形中找共同的边或角,从而得到一些等量关系,来解决问题.

2.1 通法展示

评析本题通过设角,巧妙的将面积的最值转化为了三角函数的最值,十分巧妙.笔者也尝试设AC=x,试图用x来表示∠ADC,但是过程相比此法要复杂的多.因此本道题虽然图形简单,但无疑是起到了一个通法的示范作用.

2.2 直角三角形模型

评析遇到这类复杂的三角形问题,要求哪个角,我们就可以设哪个角为θ.值得一提的是,ΔACD是一个直角三角形,所以我们可以先从这个特殊的三角形出发,用表示这个三角形的剩下的两条边.在解法一和解法二中,我们寻找了一个新的三角形用正弦定理寻找等式.但在实际上很多同学很难确定到底在哪个三角形中有等式,于是我们有了解法三,也就是可以在两个不同的三角形中,寻找到同一条边的不同的表达,从而得到一个等式.相对来说,解法一、二的思维要求更高,解答更方便;易见,解法三解答稍有复杂,但都不失为处理复杂三角形的好方法.

2.3 外接圆模型

评析三角形外接圆模型中,学生极易忽视用正弦定理处理三角形外接圆的半径.本题出现了两个角之间的关系,那么我们往往设其中一个小角为θ.解法一是利用题目中两

评析本题要特别注意的是直径所对的圆周角是直角,圆内接四边形对角互补,剩下的思路和前面的通法完全一致,这里留给读者完成.

2.4 相似三角形模型

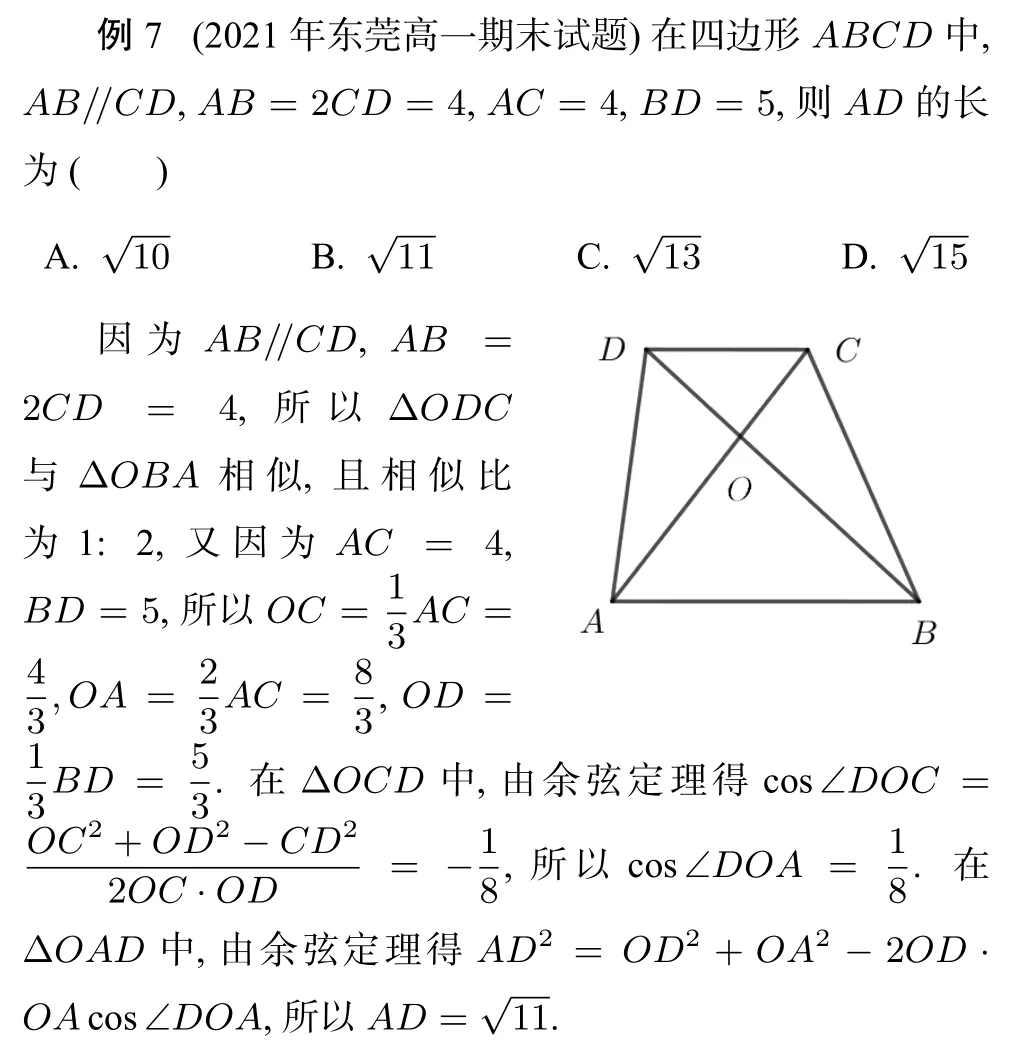
评析本题是东莞高一期末考试试题,我校的平均分才1.76,得分率35.13.这个数据充分说明高一学生对解三角形的问题尚属不得要领阶段.本题若设∠ABC=θ,依次在ΔABC,ΔBCD,ΔACD中用正弦和余弦定理,也能做出来,但花费时间显然要多的多.本题最显著的特征是,两直线平行,利用三角形相似求长度.倘若在解三角形习题课讲评时,多给两直线平行模型,也许学生会有更好的分数.

行文至此,相信大家对解三角形有了更深的认识.每年的高考题中的解三角形中的复杂平面图形问题都是难点,其实高一学生已经有所涉猎.倘若平时能够加以训练,相信对提升学生的逻辑思维大有裨益.