试用组合分析法表示广义Fibonacci数列

广东省东莞市麻涌中学(523130)吴贞霞

对于广义Fibonacci 数列的通项表示一般有三种方法,使用最多的便是采用特征方程或采用发生函数求解而得[1-5],其次还有不少学者采用类似文献[1]的行列式表示方法,且方法具有一般性.然而笔者发现很少有人采用组合分析法表示广义Fibonacci 数列通项,是否存在这样的表示方法呢?答案是肯定的,本文将采用组合分析法给出二阶广义Fibonacci数列的通项公式,并且进一步采用组合分析法研究了高阶广义Fibonacci 数列通项表示法.

1 准备

定义1数列Fn若满足Fn+1=uFn+vFn−1(u,v ∈+),F0=0,F1=1,则称数列Fn为二阶广义Fibonacci 数列.我们熟知的Fibonacci 数列实则当u=v=1 的情况.

定义2数列Fn若满足Fn=u1Fn−1+u2Fn−2+u3Fn−3,F0=0,F1=0,F2=1,则称数列Fn为三阶广义Fibonacci 数列.

定义3数列Fn若满足Fn=u1Fn−1+···+ukFn−k,F0=0,···,Fk−2=0,Fk−1=1,则称数列Fn为k阶广义Fibonacci 数列.

2 主要结论及证明

定理1若数列Fn为二阶广义Fibonacci 数列,则.

证明(用组合分析法进行证明)设G(n)表示一个司机要行驶到第n个城市的方法总数,规定

1.相邻两个城市间有u条路线可选择,称之为1 路.任意间隔一个城市的两个城市间有v条路可选择,称之为2 路,且2 路均不经过中间那个城市.

2.司机从第i个城市开至i+1 或开至i+2 个城市时都必须停车加油后才能继续前进.

3.司机每次加油后只能行驶1 个2 路,或行驶1 个1 路.

显见G(1)=1,G(2)=u,且

令G(0)=0,则

因此数列(2)与二阶广义Fibonacci 数列有相同的初始值和相同的递推关系,从而可知G(n)=Fn(n=0,1,2,···).

事实上,我们还可以采用数学归纳法证明.这类二阶广义Fibonacci 数列在现实生活中有着数学建模的作用,并且更加贴近生活.对其研究就显得更加重要了.我们将上述定理证明过程中的模型简单地应用于该类数列的性质定理,易得以下若干结论.

定理2若数列Fn为二阶广义Fibonacci 数列,则

Fm+n=FmFn+1+vFm−1Fn.

证明由定理1 证明过程中的模型,Fm+n表示司机到达第m+n个城市的线路总数,则我们可将其分类,即司机恰好在第m个城市加油的路线总数为FmFn+1,而恰好不在第m个城市加油的路线总数为vFm−1Fn,故Fm+n=FmFn+1+vFm−1Fn,证毕.

例1数列Fn二阶广义Fibonacci 数列,且满足u=2,v=3,求数列通项公式(采用组合分析法表示)

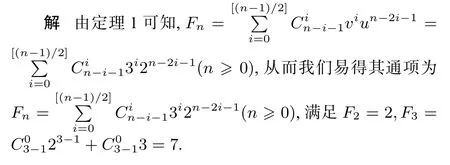
自然会问,对于高阶广义Fibonacci 数列的通项是否也能采用组合分析法进行表达呢?

本文所给出的结论均是在初始值给定的情况下而得,其实对于任意的初始值都能用组合分析法得出相关结论,只需要将上述的模型中改变前k个城市的路线数量即可,此处从略.

3 小结

采用组合分析法不仅给出了二阶广义Fibonacci 数列的通项公式,还进一步研究了高阶广义Fibonacci 数列通项公式.