相干接收机色散补偿FIR滤波器设计

朱旭飞, 陆叶*, 李传起, 武康康, 陈东, 孔一卜

(1 广西师范大学电子工程学院光电子与光通信实验室, 广西 桂林 541004;2 南宁师范大学物理与电子学院, 广西 南宁 530001;3 中国电子科技集团公司第三十四研究所, 广西 桂林 541004)

0 引 言

由于光纤中存在群速度色散(GVD),从而引起光脉冲在时间上的展宽,造成光信号失真。光纤色散不但限制信号传输距离,还限制传输速率,是制约光纤通信向长距离、大容量和高速率发展的关键因素。随着相干检测技术、高阶调制技术以及高速模数转换器(ADC)的发展,利用数字信号处理方法来进行色散补偿已是一大趋势[1-5]。已有的色散补偿方法有时域均衡滤波器[6,7]、权重优化FIR 滤波器[8]、重叠频域均衡滤波器[9]以及最优最小二乘滤波器[10],前三种滤波器均在全频带范围进行色散补偿,所需抽头数较多,硬件成本较高,增加了滤波器总延迟,在高速光通信中尤为不利。最优最小二乘滤波器能在窄频带范围补偿,但设计复杂度过高。

本文提出了利用神经网络训练的色散补偿滤波器,能在窄频带范围进行色散补偿,具有较少的抽头数,较低的滤波器延迟。由于具有固定神经网络结构,改变系统参数即可适用于QPSK、M-QAM 等不同调制格式的系统,设计复杂度较低。

1 滤波器原理

单模光纤中色散频域传输函数为[11]

式中λ、 ω、D分别是中心波长、信号角频率和光纤色散参数,c、z、T分别是光速、传播距离和采样周期。D与GVD 参数β2的关系可表示为

根据(1)式可将光纤中的色散频域传输函数看作全通滤波器，光信号的幅度不发生变化，但增加了额外与频率有关的相移。将(1)式中D取反,可得色散补偿滤波器理想频率响应

可推导出时域均衡滤波器抽头系数公式[6,7]

定义

理想滤波器频率响应为

单位冲击响应如(8)式所示的N-1 阶FIR 数字滤波器可用来逼近(7)式,其抽头系数为复数。

频率响应为

(7)、(8)式可表示为

在[-π,π] 上取M个频率采样点ωi(i= 0,1,··· ,M-1), 为每一个ωi设置一个权重系数ai≥0 (i=0,1,··· ,M-1),使用加权平方误差e2判断(11)式逼近(10)式的程度[12-14],e2可表示为

式中

滤波器的抽头数N是有限的,因此e2不可能为0,权重系数ai的大小决定了其对应的频率ωi在整体中占有的比重,在训练过程中可选取特定的ai值使e2尽可能小,ai越大表明在ωi频率点上(11)式的值越趋近于(10)式。

可选择如下的一组权重系数

式中阻带上的权重系数值可为任意比1 大的整数,其大小可根据实际情况进行调整。

定义两个矩阵

由(15)、(16)式可得(11)式的矩阵形式

由(10)、(17)式可得

在(18)、(19)式中,cos(Kω2)、sin(Kω2)是通带上的值,0 是阻带上的值。可以看出若频率点ω 均匀地分布在区间[-π,π]上,此时可以认为滤波器是在全频带上设计的。Eghbali 等[10]推导出信号在经过脉冲成型和匹配滤波之后有效带宽的变化情况。假设脉冲成型滤波器采用L倍采样,滚降系数为ρ,此时信号的有效带宽为如果将滤波器不在信号有效带宽范围内的频率点上的值均设置为0,即作为阻带,就是实现了滤波器的窄频带设计。

使用梯度下降法可以实现矩阵WR、WI中数值的更新[15]。迭代公式为

式中WRk、WIk分别表示向量WR、WI的第k+1 个元素,η 表示学习速率,文中取0.05。由(7)式可看出,理想频率响应的幅度恒定,其相位为频率的二次函数。因此平方误差e2达到最小的值并不为0。由于所需的目标滤波器抽头数为奇数个,且关于中心频率点呈偶对称。因此可得纠正公式

根据(24)、(25)式可得Wk,把Wk作为滤波器抽头系数h(n)。在下文中为表述简洁,用(4)表示时域均衡滤波器,(25)表示利用神经网络训练的色散补偿滤波器,BTB 表示背靠背系统。

2 数值仿真及分析

由(18)、(19)式可知,神经网络的训练过程可看作两个矩阵的乘积,矩阵可作为神经网络训练的样本,矩阵[WRWI]T是两个式子共有的因数,因此设计出的神经网络结构如图1 所示, 该结构左侧为输入端,中间为隐藏层,右侧为输出端,箭头上标注的是各端口上的权值。其中，输出端的权值排列构成了矩阵[WRWI]T。由上面的推导可以看出,神经网络中参与计算的值不包含虚数,这大大减少了网络的计算量。由(12)式可以看出,误差函数为权值矩阵的二次函数,因此若学习速率取适当的值,在训练后神经网络必定能收敛,且能取得全局最小值。

用MATLAB 搭建图2 所示的QPSK/QAM 仿真系统模型。用平方根升余弦滤波器实现脉冲成型及匹配滤波。光纤色散及非线性效应使用分步傅里叶方法进行模拟。在系统中不考虑光纤衰减,通过向传输信号中混入不同的高斯白噪声来测量系统的性能。

图1 神经网络结构Fig.1 Neural network structure

图2 QPSK/M-QAM 仿真系统模型Fig.2 QPSK/M-QAM simulation system model

表1 为设置的系统仿真参数,调制后的QPSK/QAM 信号将会分两路,即同相分量和正交分量。仿真实验结果表明,调制阶数和用户速率呈正相关,即调制阶数增大，用户比特速率也会增大。假设已调信号的星座图中坐标点数为M,通过表中列出的单路信号的符号率可以计算得出实际用户的比特速率是25 log2(M)bit/s,过采样率不仅会影响光纤的色散程度,而且决定了脉冲成型滤波器的上采样倍数。传输信号的有效带宽则受滚降系数和过采样率值的影响。假设滚降系数为ρ,上采样倍数为L,则信号的有效带宽范围为将区间[-π,π]称为全频带。

表1 QPSK/QAM 系统仿真参数Table 1 Simulation parameters of QPSK/QAM system

2.1 全频带

脉冲成型滤波器的过采样率设置为L= 2,滚降系数设置为ρ = 1,此时信号的有效带宽为[-π,π],(4)、(25)式均表示全频带上设计的滤波器。将系统的调制格式设置为16QAM,通过(5)式计算得到滤波器抽头数为315。图3 为在滤波器抽头数都是315 时,(4)、(25)表示的滤波器抽头系数模值|h(n)|,由图可见,(4)的模值是恒定的,这会给均衡效果带来较大影响[8]。

图3 (4)和(25)抽头系数的模值,N =315Fig.3 The tap coefficient modulus values of(4)and(25),N =315

将系统的信噪比RSN分别设置为10、12、14 dB,抽头数依次设置为305 ～405 的整数值,研究在不同的抽头数影响下滤波器均衡效果的变化情况,仿真结果如图4 所示(RBE表示误码率）。图中分别对(4)、(25)及背靠背(BTB)系统进行了仿真,从图中可看出,当抽头数增加时,(4)的均衡效果反而变坏,特别是当信噪比较高时,这种变坏的趋势更明显。(25)的均衡效果与抽头数有一定的关系,在抽头数增加的情况下,其均衡效果会比(4)更易趋于稳定。当信噪比取三种不同的值时,在抽头数相同的情况下,(25)的均衡效果比(4)更好。总之,改善(25)的均衡效果可以通过增加抽头数来实现,但是会有一个上限值,却又不像(4)会出现增加抽头数而均衡效果劣化的现象。

设置抽头数为315,在QPSK、16QAM 及64QAM 调制格式的系统中仿真(4)、(25)两种滤波器,观察在信噪比变化时系统误码率的变化情况。图5 为仿真结果，观察图5 可知,无论系统为何种调制格式,(25)相较于(4)其均衡效果都更优。当调制格式的阶数增加时,(25)比(4)具有更突出的优越性。当系统的调制格式为16QAM 时,若信噪比超过16 dB,(4)、(25)均衡后系统的误码率均最终稳定到一个恒定值。因为仿真中的用户总比特数设置为120000,所以系统的误码率最终无限逼近10-5。此外,非线性效应对系统也有一定的影响[16,17]。

2.2 窄频带

设置脉冲成型滤波器过采样率L=2,滚降系数ρ=0.25,此时信号有效带宽范围为表示的滤波器可在信号有效频带内设计。将系统的调制格式设置为16QAM/64QAM,此时利用(5)式计算得出(4)式表示的滤波器的抽头数为315,将(25)式表示的滤波器的抽头数设置为197。仿真实验结果如图6 所示。由图可见,当系统的调制格式为16QAM/64QAM 时,(25)滤波器的抽头数比(4)下降37.5%,但是仍具有更好的均衡效果。由于(25)滤波器的抽头数相对较少,所以其在硬件实现复杂度上的要求较低,这样可以节约一部分硬件成本。此外,由于(25)有较低的滤波器延迟,故更适用于有较低延迟要求的高速光通信系统。

图4 不同的抽头数目对滤波器均衡效果的影响Fig.4 Effect of different tap numbers on filter equalization effect

图5 在三种调制格式下(4)和(25)滤波器的均衡效果Fig.5 Equalization effect of(4)and(25)in three modulation format systems

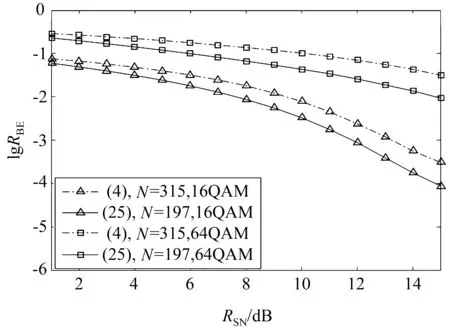
图6 滤波器(25)更少抽头系数的影响Fig.6 Effect of filter(25)with fewer taps

3 结 论

提出了利用神经网络训练的色散补偿滤波器,推导了滤波器的原理。通过分析得出,经训练后的神经网络一定会收敛到全局最小值, 这避免了有可能会陷入局部最小值的风险。利用MATLAB 分别对QPSK、16QAM 和64QAM 这三种系统中的滤波器性能进行了仿真实验。实验结果显示在全频带和窄频带中,与时域色散均衡器相比,所提出的滤波器均衡效果更好。此外,当信噪比增加时,所提出滤波器会有更大的领先优势。假设滤波器在窄频带中进行设计,那么与时域色散均衡器相比,抽头数可降至原来的62.5%，却能获得更好的均衡效果。抽头数的降低使其在硬件实现复杂度方面的要求较低,同时,其滤波器的延迟也有一定下降。这适用于设计有高速率、低延迟及低成本要求的相干光通信系统。