公铁平层超宽钢箱梁-列车系统气动参数数值模拟研究
2021-02-25段青松李建兴吴再新
段青松 李建兴 吴再新
(1.西南交通大学力学学院,成都 610041;2.四川省铁路产业投资集团有限责任公司,成都 610041)
横风作用下列车受到的气动力是影响其横向振动和安全性的关键荷载,受基础设施(如桥梁、路堤)的影响较大。原因是列车改变了桥梁主梁的气动绕流,而主梁的几何外形会对列车所受气动荷载产生影响,列车与主梁存在明显的相互气动作用。
流线形钢箱梁具有良好的截面外形,常用于大跨度桥梁中,其断面特征见表1。对于超宽的流线形钢箱梁断面,气流在主梁迎风侧产生分离后可能会再次附着,从而对车-桥系统的气动力特性产生一定的影响,因此有必要对超宽流线形钢箱主梁及列车系统气动特性展开研究。
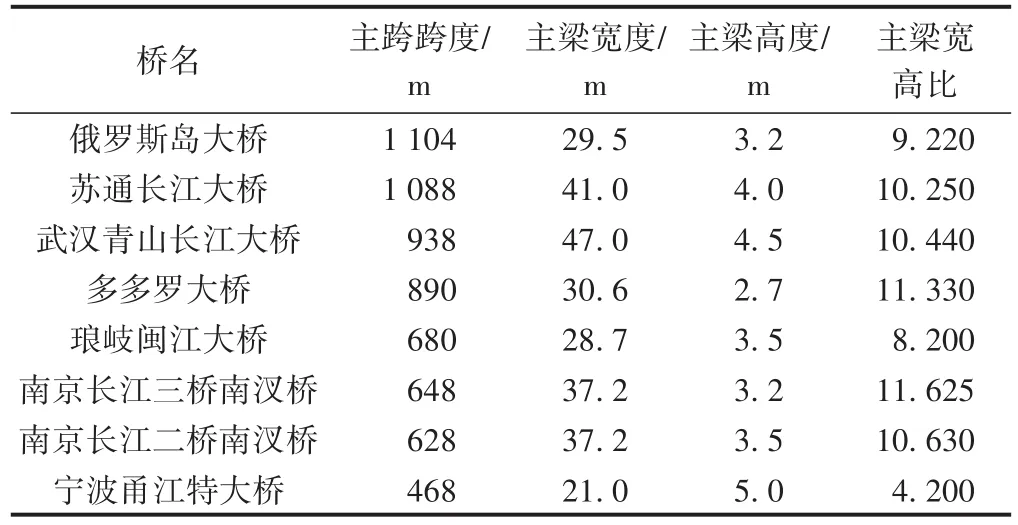
表1 大跨度斜拉桥流线形钢箱主梁断面特征
许多学者对横风中列车平均气动力系数进行了研究。文献[1]研究了不同截面类型主梁以及列车位置对列车所受平均气动力的影响。文献[2]分析了流线形截面主梁上不同类型列车所受平均气动力。文献[3]通过风洞试验分析了紊流风对列车所受平均气动力的影响。文献[4-5]基于节段模型对车-桥系统中列车的气动性能进行了分析。
在大气紊流风作用下,除了平均气动力,列车还会受到抖振力,气动导纳是抖振力的一个重要气动参数。文献[3]基于风洞试验的测压法得到不同紊流积分尺度和不同风偏角条件下列车的气动导纳函数。文献[6]基于准定常假定且考虑二阶修正理论,通过实地测量得到了列车气动导纳函数,并探讨了风偏角的影响。文献[7]总结了不同类型列车的气动导纳并拟合了列车气动导纳函数。文献[8]提出了列车气动导纳的数学模型并通过风洞试验进行了验证。
上述关于列车气动导纳的研究存在2个问题:①研究多集中于列车位于平地的情况,关于桥梁上列车气动导纳的研究相对较少;②研究多针对列车三维气动导纳函数,受紊流积分尺度、紊流度等参数影响较大,但列车作为细长的结构物运行于桥梁之上,其二维气动导纳函数有待于进一步研究。
本文以一座在建大跨度公铁平层超宽流线形钢箱梁斜拉桥为工程背景,对车-桥系统列车、桥梁主梁的气动力特性(平均气动力系数和气动导纳函数)进行数值模拟并研究。
1 气动力系数数值模拟
公铁平层超宽流线形钢箱梁断面如图1所示,主梁截面宽63.9 m,高5.0 m,宽高比为12.78。其中,左右车道为公路,中间Ⅰ车道—Ⅳ车道为铁路。
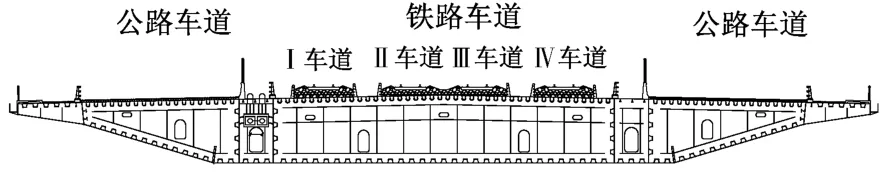
图1 流线形钢箱梁断面
采用FLUENT软件进行数值模拟,计算方法为:时间离散采用二阶隐式;对流项为二阶迎风格式,其他流动物理量的空间离散采用二阶格式;方程组求解时采用SIMPLEC算法,采用SST k-w流模型,连续性方程的收敛值为1×10-6;无量纲时间步长为2×10-4,以确保柯朗数小于1,并保证每步计算在20次迭代内完成。
模型的计算区域如图2(a)所示,B为主梁截面宽,计算域长度为18B,宽度为6B。计算域左侧边界为速度入口条件,上下边界为无滑移的Wall边界条件,右侧边界为压力出口边界条件,结构表面为无滑移的Wall边界条件。网格采用结构化体系网格,为保证计算精度和效率,断面周围1.5B的圆形区域采用贴体网格,远离断面的区域采用稀疏网格。靠近断面的第1层网格尺寸为5×10-5B,并以1.03指数增长率向外延伸。对栏杆、列车周围的网格加密,总网格数为6×105,数值网格划分如图2(b)所示。
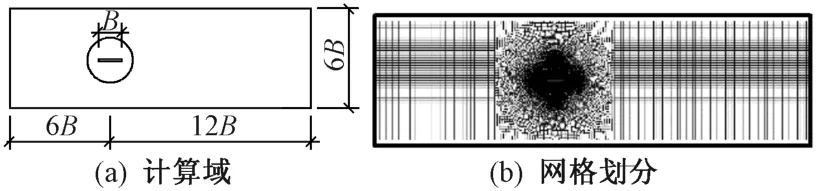
图2 数值模拟设置
计算时取截面的高度为阻力系数的特征尺寸,宽度为升力系数或力矩系数的特征尺寸。体轴坐标系下,0°风攻角时列车及主梁气动力系数数值模拟与试验结果对比见表2。其中,CD,CL,CM分别为体轴坐标系下阻力系数、升力系数和力矩系数。可知,数值模拟值与试验值吻合较好,验证了数值模拟方法的可靠性。

表2 列车及主梁气动力系数数值模拟与试验结果对比
1.1 列车位置对车-桥系统三分力系数的影响
车-桥系统中列车与主梁气动力会相互影响。因此,分析来流风攻角为0°时,列车位置对车-桥系统三分力系数的影响,见表3。

表3 列车位置对车-桥系统三分力系数的影响
由表3可知:
1)列车位于Ⅰ车道时,分离气流直接作用于列车,主梁受到的气动影响小,其阻力系数比单独主梁(桥上无列车)的阻力系数小。列车位于Ⅱ车道—Ⅳ车道时,列车气动力减小,主梁阻力系数逐渐增大。原因是当列车位于Ⅱ车道—Ⅳ车道时,桥梁断面钝化,气流在桥梁迎风侧栏杆处分离,使列车的阻力系数降低。Ⅲ车道—Ⅳ车道的列车阻力系数比较接近,且比列车位于Ⅱ车道时小,原因是气流在桥梁迎风侧分离,桥梁宽度较大,而位于Ⅲ车道—Ⅳ车道时列车距离桥梁迎风侧较远,其气动影响基本一致。
2)当列车位于Ⅰ车道时,列车阻力系数比列车位于其他车道时大。列车位于Ⅲ车道—Ⅳ车道时,主梁升力系数变化相对较小。
3)列车位于Ⅰ车道时,列车及主梁的力矩系数绝对值相对最大;列车位于Ⅱ车道—Ⅲ车道时,列车及主梁力矩系数较接近;列车位于Ⅳ车道时,列车力矩系数比Ⅱ车道—Ⅲ车道时略有增大,主梁力矩系数略有减小。与阻力及升力系数相比,列车及主梁力矩系数变化幅度相对较小。
1.2 风攻角对车-桥系统三分力系数的影响
桥梁断面钝化可能引起气流分离后上部分离流重新附着于列车。由于来流风攻角不同,导致气流流经钝体断面后的剪切层厚度不同,进而对气流再附着车辆产生的气动力有一定影响。不同风攻角下列车的阻力系数,见表4。
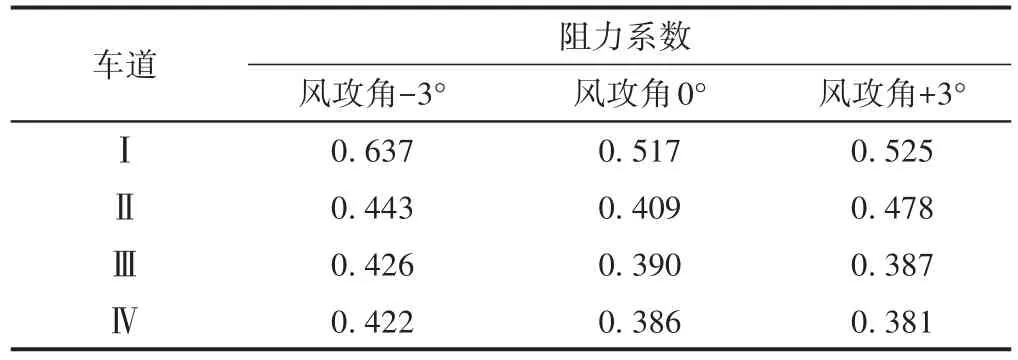
表4 不同风攻角下列车的阻力系数
由表4可知:风攻角为-3°~+3°时对列车阻力系数的影响相对较小。列车位于Ⅰ车道—Ⅳ车道时的阻力系数逐渐减小;风攻角为-3°时,列车迎风面积增大,桥梁迎风侧栏杆处的分离减弱,列车阻力系数比风攻角为0°,+3°时大;不同风攻角下,位于Ⅲ车道—Ⅳ车道的列车阻力系数较接近。
本文数值模拟结果均为列车静止于桥梁主梁的结果。根据文献[9]可知,列车运行在平坦的地面上时气动力系数会发生一定变化,变化幅度约在10%以内。列车运行于桥面时,钝体主梁断面可能对列车气动特性产生较大影响。
2 气动导纳数值模拟
边界条件:计算域左侧边界为速度入口条件,水平向速度保持恒定不变,竖向速度随时间简谐变化,通过用户自定义函数编程实现竖向速度变化;上下边界为无滑移的Wall边界条件;右侧边界为自由出流边界条件;结构表面为无滑移的Wall边界条件。
升力气动导纳χL(k)计算式为
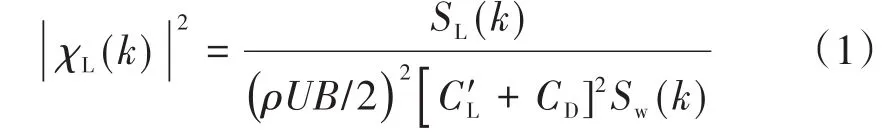
式中:SL(k)为升力力谱;k为无量纲的折减频率,k=fB/U,f为频率;U为来流平均风速;ρ为空气密度为升力系数对风攻角的导数;Sw(k)为风谱。
2.1 气动导纳数值模拟验证
建立宽为1.00 m,高为0.01 m的矩形平板,平板的阻力系数为0,升力系数斜率为2π。来流边界条件为:水平向为均匀流,风速为10 m/s;竖向为单频率的简谐波,幅值为0.336 m,湍流强度为2%。简谐脉动速度为单向的,时间步长为0.002 s。
平板气动导纳数值模拟见图3。可知,在高折减频率与低折减频率时,平板气动导纳的数值识别结果与根据势流理论推导的Sears函数吻合较好,可认为该数值识别方法可靠。

图3 平板气动导纳数值模拟
2.2 二维气动导纳函数数值模拟结果
正弦风场中,成桥状态主梁二维升力气动导纳见图4。可知,流线形钢箱梁的二维升力气动导纳比Sears函数略小,但二者数值基本一致,说明主梁二维升力气动导纳可用Sears函数表示。
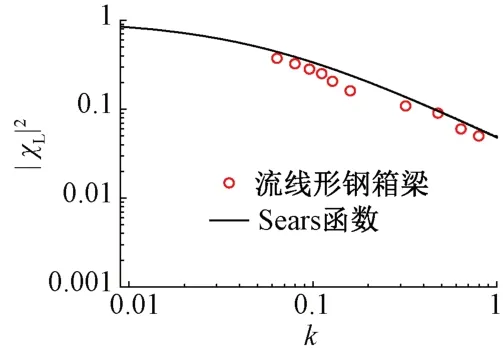
图4 主梁二维气动导纳
一列高速列车通常由多节车厢组成,中部车厢形状不变,故一般按头车、中车和尾车分类。本文主要针对列车的中车进行研究。列车模型底部忽略转向架等影响,简化为平面,且未考虑受电弓等构件。
静止列车二维气动导纳见图5。可知:①列车升力气动导纳比Sears函数偏大,但变化趋势基本一致。在折减频率小于0.05时,气动导纳接近1。随着折减频率的增大,气动导纳逐渐减小。②主梁上列车升力的气动导纳比单独列车升力的气动导纳小,比Sears函数略大。这说明不考虑主梁的影响,单独进行列车气动导纳分析是不准确的。
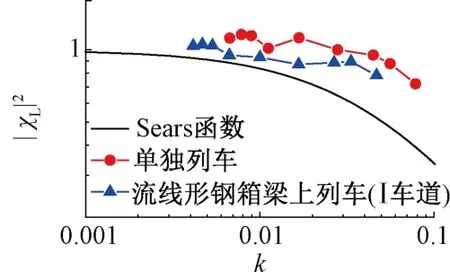
图5 静止列车二维气动导纳
对于无限展长的模型,其气动导纳函数为二维的[10]。当来流紊流相关性较好时,三维与二维气动导纳函数趋于一致。因此,对于多个编组的列车,其为细长结构物,结构长度远大于宽度,可以考虑用二维气动导纳分析车-桥耦合作用。
3 结论
1)迎风侧(Ⅰ车道)列车距离桥梁前缘较近,直接受来流风的作用,背风侧(Ⅱ车道—Ⅳ车道)列车距离桥梁前缘较远,桥梁断面钝化,气流在桥梁迎风侧栏杆处分离,故迎风侧列车的阻力系数比背风侧时大。
2)气流在桥梁迎风侧分离,当桥面宽度较大,列车位于Ⅲ车道—Ⅳ车道时,列车阻力系数比较接近。
3)平板升力气动导纳的数值模拟结果与Sears函数高度吻合,证明了数值模拟方法的正确性和可行性。超宽流线形钢箱梁断面升力气动导纳比Sears函数略小,但基本一致。桥梁上列车升力气动导纳比单独列车升力气动导纳偏小,比Sears函数略偏大,且随折减频率的增大而逐渐减小。
