GNSS与惯性导航组合系统在复杂环境下的定位研究

程保喜

(山西省信息产业技术研究院有限公司，山西 太原 030012)

0 引 言

随着现代科学技术的发展，人们对动态载体(车辆、飞机、导弹等)的追踪精度要求越来越高.全球卫星导航系统(GNSS)能够提供全天时的位置时间信息，精度不会随时间而变化，但信号在遮挡时会造成定位不准确.惯性导航系统不受外界环境制约，短时间内位置、速度等导航参数能够以较高精度输出，但随着时间积累其定位精度会明显下降，不能长时间单独工作.GNSS差分定位与惯性导航系统具有互补性，组合后可以提高GNSS接收机跟踪卫星的能力和抗干扰性，及惯性导航系统稳定的性能和精度.自20世纪80年代起，国内外开始对GNSS与惯性导航组合系统进行研究，美国斯坦福大学对于惯性导航系统辅助GNSS接收机载波跟踪环路研究工作比较深入；国内杨春钧教授研究了差分GNSS伪距和载波相位与惯性导航系统的组合定位情况，认为载波相位与惯性导航系统的组合可获得更好的效果.

在目前机动车驾驶人考试中，普遍采用的评判技术是基于GNSS差分定位技术，该技术具有精度高(能够达到厘米级)、成本低及可靠性好等特点，但一些复杂环境条件会对其定位效果影响较大.例如在考试过程中机动车通过高架桥、高楼、隧道以及有茂盛树木遮挡的复杂路段时，会出现信号较差或完全没有信号，定位精度误差可达到数十米，会对驾驶人考试造成错误的评判，GNSS差分定位的良好应用必须保证能够接收到信号源[1-4].为解决上述问题，将GNSS差分定位与惯性导航进行组合.本文对组合系统中的定位技术进行分析，将GNSS差分定位与惯性导航进行组合，并在复杂环境中(隧道、高架桥等)进行实验，与单独惯性导航系统进行对比，验证组合导航的实用性和可靠性.

1 GNSS差分定位与惯性导航原理分析

全球卫星定位系统GNSS是北斗导航、GPS、格洛纳斯、伽利略卫星导航定位系统的相加增强型系统.GNSS差分定位的工作原理是建立在基准站及移动站的载波相位上，载波相位差分和基站三维坐标信息通过基准站传递给移动站，移动站接收到GNSS的载波相位以及基准站的信息后进行及时处理并对其求差解算，从而得到高精度的定位结果.在定位过程中利用差分技术可以完全消除卫星时钟误差、星历误差、电离层误差以及对流层误差[5-8].

对于观测到的GNSS伪距和载波相位数据，其观测方程为[9]

p=ρ+c(dT-dt)+Δρi+Δρτ+V1,

(1)

λ(φ+N)=ρ+c(dT-dt)-Δρi+Δρτ+V2,

(2)

对式(1)和式(2)进行差分处理得到

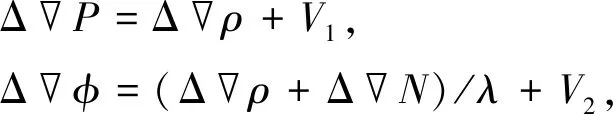
(3)

经过两次差分后去除了电离层、对流层、卫星星历以及接收机钟差的影响.

最小二乘法和卡尔曼滤波法是GNSS差分数据处理中最常使用的方法[10].最小二乘法使用静态模型，在对GNSS差分数据处理时无需取得车载移动端的信息数据.但在GNSS差分定位中，车载移动端是动态系统，其信息数据在不停地变化，最小二乘法不能精确观测到不同时刻的系统状态[11].卡尔曼滤波法是一种能够对观测数据进行还原的方法，通过对系统的输入和输出数据的观测，能够对系统的状态进行预测估计，并对实时采集到的数据进行处理，算法采用递推模式[12].通过卡尔曼滤波法和最小二乘法的对比可知，卡尔曼滤波法进行GNSS差分定位数据处理更加合适[13].

卡尔曼滤波的状态方程为

XK=φKK-1XK-1+ΓK-1WK-1,

(4)

观测方程为

ZK=HKXK+υK，

(5)

状态预测估计方程为

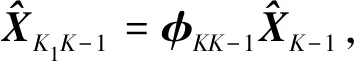
(6)

方差预测方程为

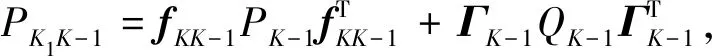
(7)

状态预测估计方程为

XK=XKK-1+KK(ZK-HKXK1K-1)，

(8)

方差迭代方程为

PK=(1-KK*HK)PK1K-1，

(9)

滤波增益方程为

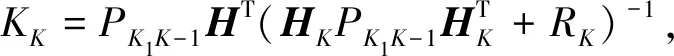
(10)

初始条件为

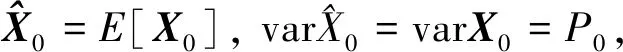
(11)

验前统计量为

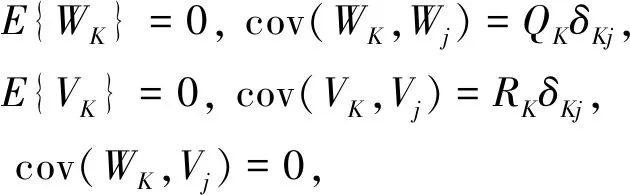
(12)

式中：φ为状态转移矩阵；X为参数的状态向量，

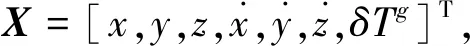
(13)

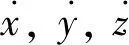
惯性导航系统是不依靠外部信息的自主式推算导航系统，其根据已知点的位置航向角和速度可推算出下一点的位置.惯性导航系统主要由陀螺仪和加速度计组成.陀螺仪形成导航系统，加速度计测量运动载体的加速度，通过积分得到速度和位移，在运动过程中，要计算出载体坐标以及导航坐标，并分析它们之间的关系.将东北天坐标系取为导航坐标系，陀螺仪计算出的载体坐标对导航坐标的角度变化率为

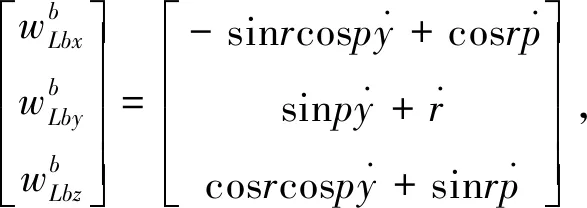
(14)

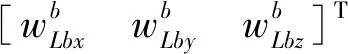
(15)

俯仰角、横滚角及航向角分别由载体中的x轴、y轴、z轴的陀螺测得.通过陀螺仪测到的角度变化率，因俯仰角和横滚角可以不考虑，载体导航坐标系的转换矩阵为[14-17]

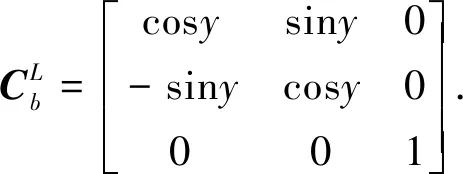
(16)

导航坐标系中速度增量为

(17)

载体的速度增量为

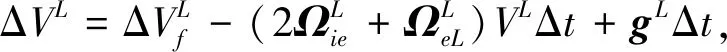
(18)

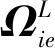
2 GNSS与惯性导航组合分析

GNSS与惯性导航组合系统在复杂环境下的定位定姿具有以下特点：

1) 整个系统可靠性高.GNSS与惯性导航进行组合的定位定姿系统中，当其中一个传感器出现问题时，另一个的传感器依旧可以工作.

2) 定位定姿精度高.在GNSS与惯性导航进行组合的定位定姿系统中，当不同的传感器在载体上完成安装后，可以利用相互之间的关系对系统定位的准确性进行核验，能够快速核验系统是否异常，组合系统的定位定姿精度较高[18].

在接收机信号缺失的条件下，惯性导航系统的位置与速度可对GNSS接收机进行跟踪环的辅助.卡尔曼滤波器会对初始状态下的GNSS测量信息进行解算，解算出的速度和位置等信息将传送到惯性导航卡尔曼滤波器中进行惯性导航的解算，根据滤波得到的误差估算值在导航解算过程中进行即时修正误差，修正后的惯性导航系统的输出为组合导航系统的结果.该方法能够避免由于误差积累导致模型失真，图1为组合系统流程图.

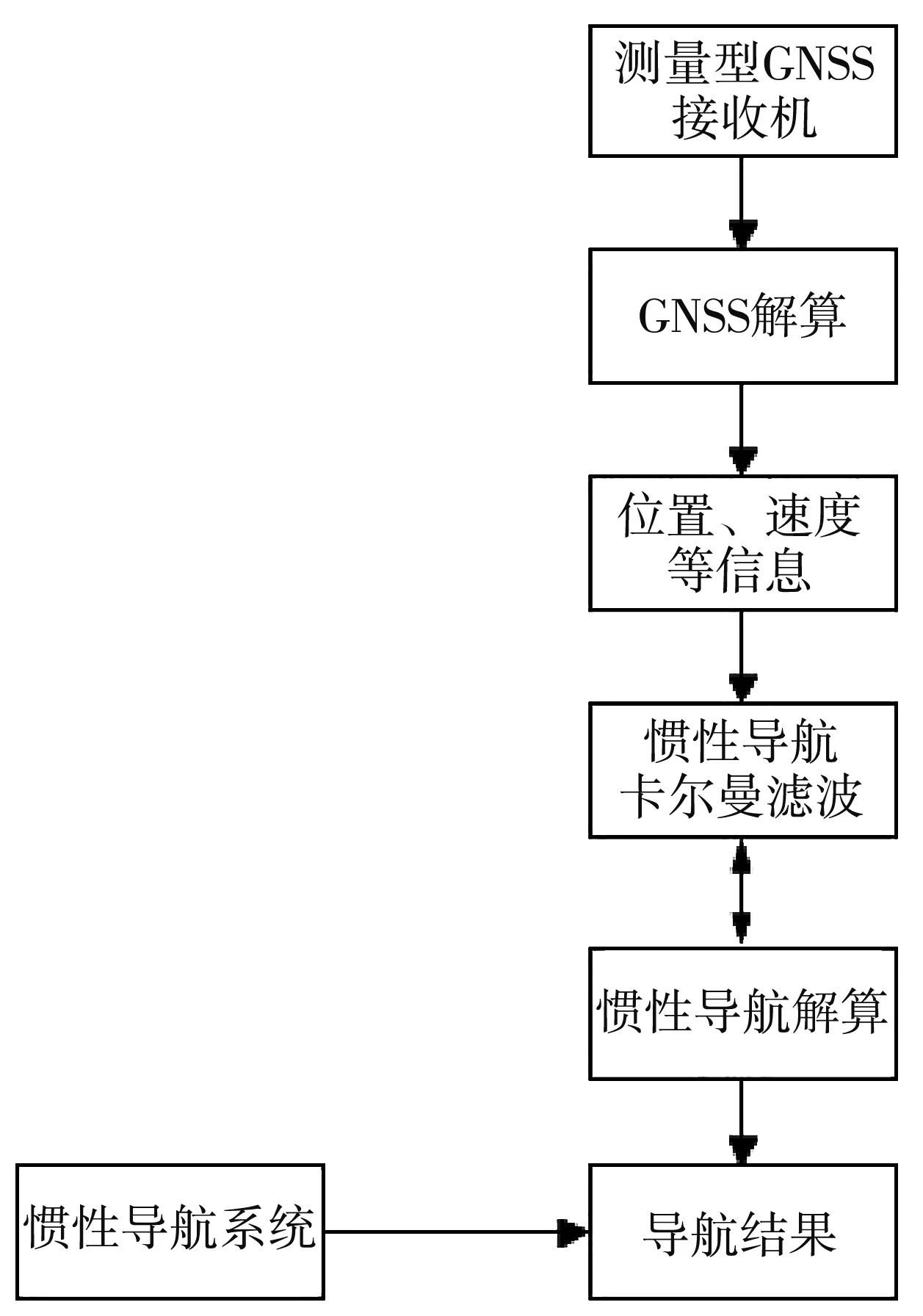
图1 组合系统流程图Fig.1 Flow chart of combined system

对GNSS与惯性导航组合系统建立误差模型，系统模型使用卡尔曼滤波器，位置、速度及姿态等状态量的误差方程为

(19)

本次惯性导航系统设计主要考虑随机误差，不考虑导航系统中的刻度误差和安装误差.

陀螺仪误差模型为

δwb=bg+sg+wg,

(20)

式中：wg为陀螺白噪声；bg为陀螺的零偏；sg为陀螺的比例因子.

加速度计误差模型为

δf=ba+sa+wa,

(21)

式中：wa为加速度计白噪声；ba为加速度计的零偏；sa为加速度计的比例因子.

惯性导航系统的状态方程为

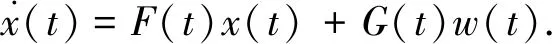
(22)

由陀螺仪误差模型中可以得到F(t)，由加速度计误差模型中可以得到G(t).

GNSS与惯性导航组合系统中的位置和速度模型分别为

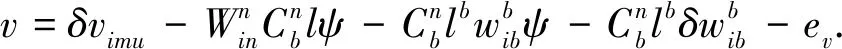
(23)

3 仿真试验与分析

3.1 惯性导航系统单独测量分析

本次实验将惯性导航系统中的陀螺仪和加速度计分别安装在车辆载体的不同方向(X轴、Y轴、Z轴).车辆在运行过程中，陀螺仪测定载体运动角速度，加速度计测定载体运动加速度，通过积分处理信息进行导航计算.实验中采用的惯性测量传感器的性能指标如表1所示.

表1 性能指标Tab.1 Performance index

当惯性导航系统单独测量时，载体的位置误差和速度误差如图2和图3所示.

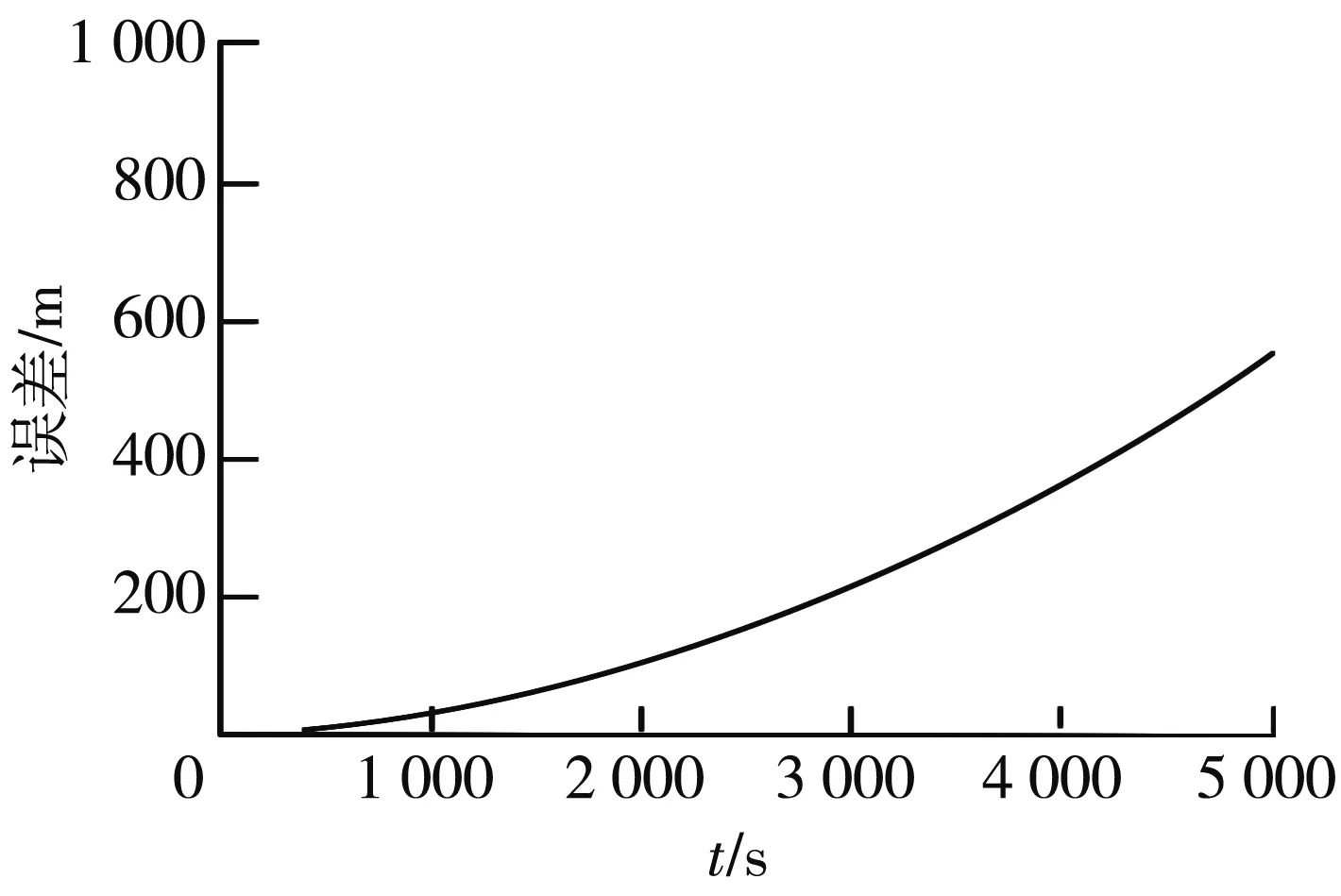
(a) 东向

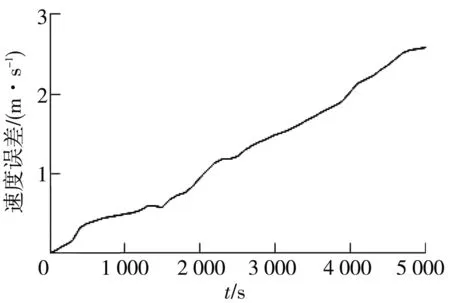
(a) 东向

从位置误差和速度误差仿真图可以看出，随着时间的积累，惯性导航系统的测量精度及定位输出会逐渐降低.下面利用GNSS接收机的信息限制惯性导航系统的误差累积，同时利用惯性导航系统的输出信息辅助接收机快速获取卫星信号.

3.2 组合导航系统试验与分析

组合导航系统会对初始状态下的GNSS测量信息进行解算，运用卡尔曼滤波器估计系统的误差状态，通过得到的结果对系统进行误差补偿.

为了充分利用GNSS原始观测数据，并且能在可观测的卫星数量少于4颗情况下进行精确定位，GNSS与惯性导航组合系统采用综合卡尔曼滤波器，该滤波器能估算GNSS与惯性导航的误差信息[19].组合导航系统流程图如图4所示.

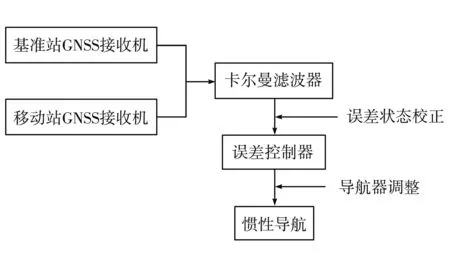
图4 组合导航系统流程图Fig.4 Flow chart of integrated navigation system

惯性导航提供速度及角度增量信息，移动站GNSS接收机提供考试车辆的双频观测信息及可视卫星的星历信息，实现考试车动态测距和测向.基准站GNSS接收机提供基准站处的观测信息和可视卫星的星历信息，作为移动差分过程中修正误差的依据.误差控制器通过卡尔曼滤波器产生的导航误差信息计算导航改正信息，并将其反馈到惯性导航解算中，该系统能将GNSS信息与惯性导航信息相互校准进行连续定位，以提供准确的定位信息.

卡尔曼滤波控制系统状态方程和量测方程表达式为

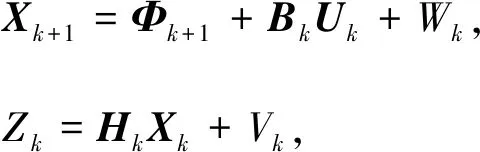
(24)

式中：Uk为控制输入矢量；Bk为n×r阶分布矩阵.

车载试验所用GNSS板卡为司南导航三系统双频双天线高精度定位板卡，将接收到的GNSS信号输入到此板卡中获取差分定位定向、姿态解算等信息，数据采样率为1 s，惯性导航系统的数据采样率为100 Hz，惯性导航系统初始姿态如表2所示.

表2 初始姿态Tab.2 Initial attitude

本次实验在晋城市机动车驾驶人考试路段进行测试，该考试路段整体接收GNSS信号较好，但会通过高架桥、高楼以及有茂盛树木遮挡的复杂路段.图5为测试路线.

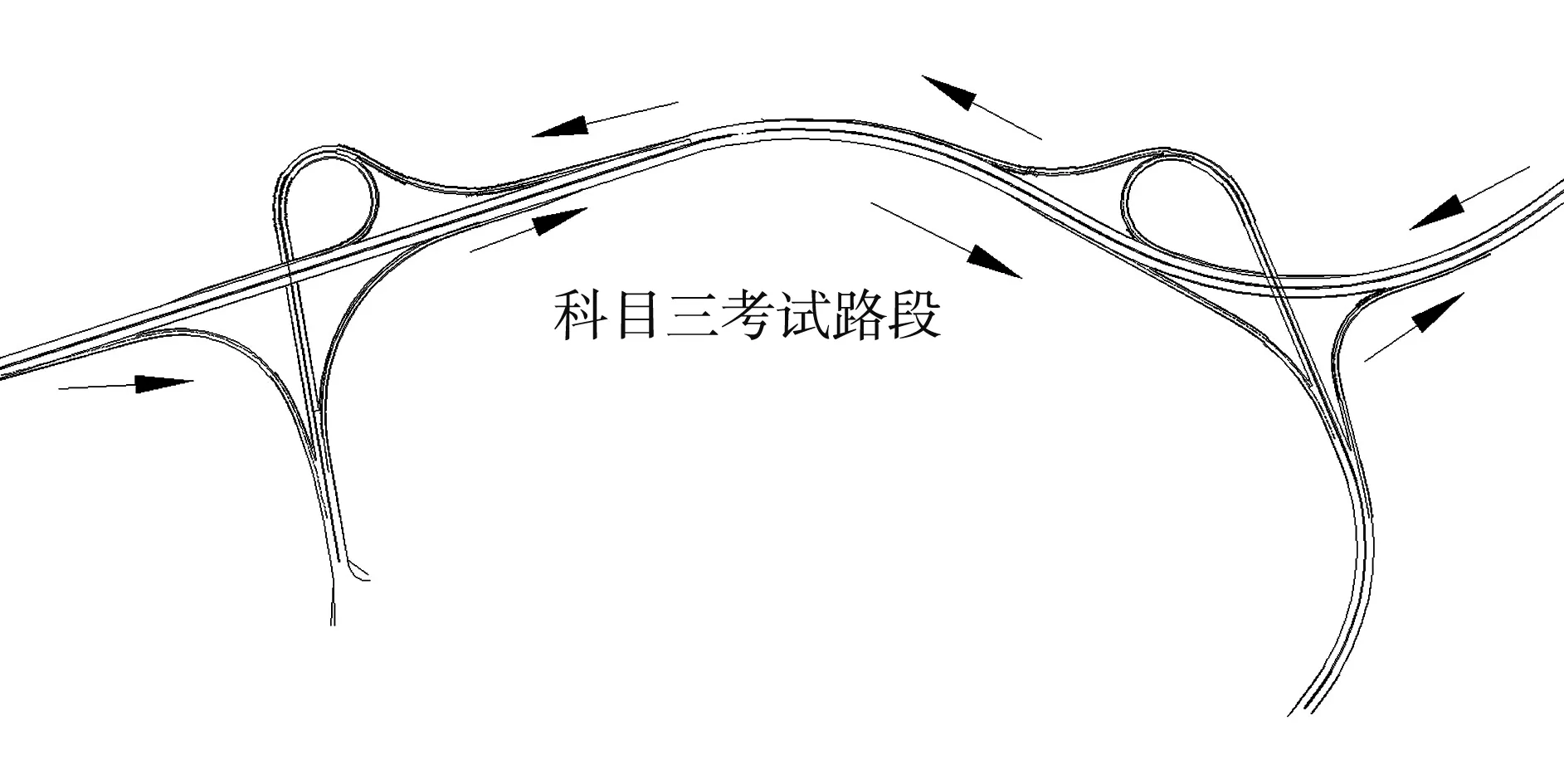
图5 测试路线Fig.5 Test route

车辆在考试路段运行一圈，定位初始结果与经角度融合处理后的结果如图6所示.

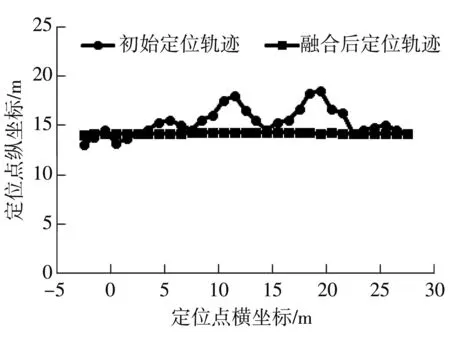
图6 信号遮挡定位结果对比Fig.6 Comparsion of signal occlusion location results

从图6结果对比看，大部分路段GNSS信号接收良好，车辆行进路线无遮挡，初始定位轨迹与融合后的轨迹相差不大.当车辆运行到高架桥、高楼以及有茂盛树木遮挡的复杂路段时，GNSS卫星信号被遮挡，接收到的卫星数量急剧下降，GNSS定位精度下降，会出现定位轨迹偏离的情况，通过与惯性测量传感器的角度融合，将偏离的轨迹点位拉回到了车辆正常行进的路线，使车辆定位的稳定性得到提升.表3分析了车辆在有遮挡的复杂路段的定位误差和定位方差.

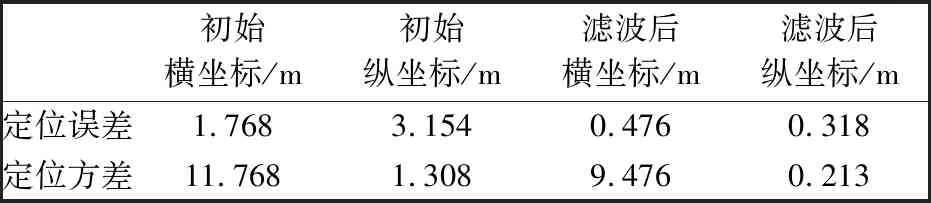
表3 信号遮挡路段误差分析Tab.3 Error analysis of signal loss section

由表3可以看出，在卫星信号有遮挡的路段经过惯性测量传感器角度融合后的定位误差小于初始定位误差，经融合后的定位方差也小于初始的定位方差，经过融合后的定位轨迹与车辆在考试路段的真实行进路线基本一致，定位精度在0.6 m 以内，说明车辆在经过高架桥、高楼以及有茂盛树木遮挡的复杂路段时，GNSS与惯性导航组合系统保证了定位的可靠性和稳定性.

3.3 仿真验证与分析

为了验证GNSS与惯性导航组合系统在复杂环境下的导航精度，进行了仿真实验，模拟汽车在道路上行驶一段距离，采用的轨迹由转弯、加速、爬升组成.

仿真参数设置如下：GNSS接收机的输出频率为20 Hz，速度随机噪声为0.05 m/s，位置随机噪声为5 m，加速度计常值零偏为10-3g，加速度计随机噪声为10-4g，陀螺仪常值漂移为0.1 °/h，陀螺仪随机噪声为0.02 °/h，输出频率为20 Hz.仿真结果如图7和图8所示，分别为卡尔曼滤波估计的速度及位置误差.

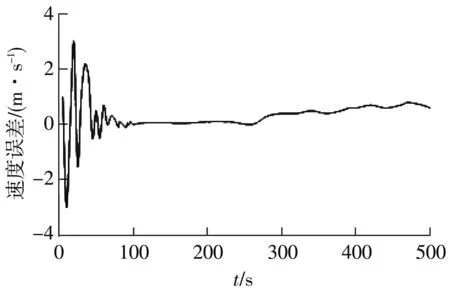
(a) 东向

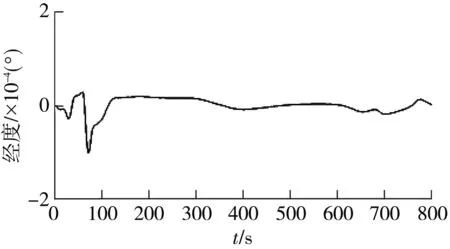
(a) 经度方向

由设定的仿真参数及仿真实验出的轨迹可以看出，在0 s～200 s内，载体进行大转弯等运动时会造成搜星数目骤降的情况，经过卡尔曼滤波估计的误差补偿量进行误差修正后，输出的结果如图9和图10所示.

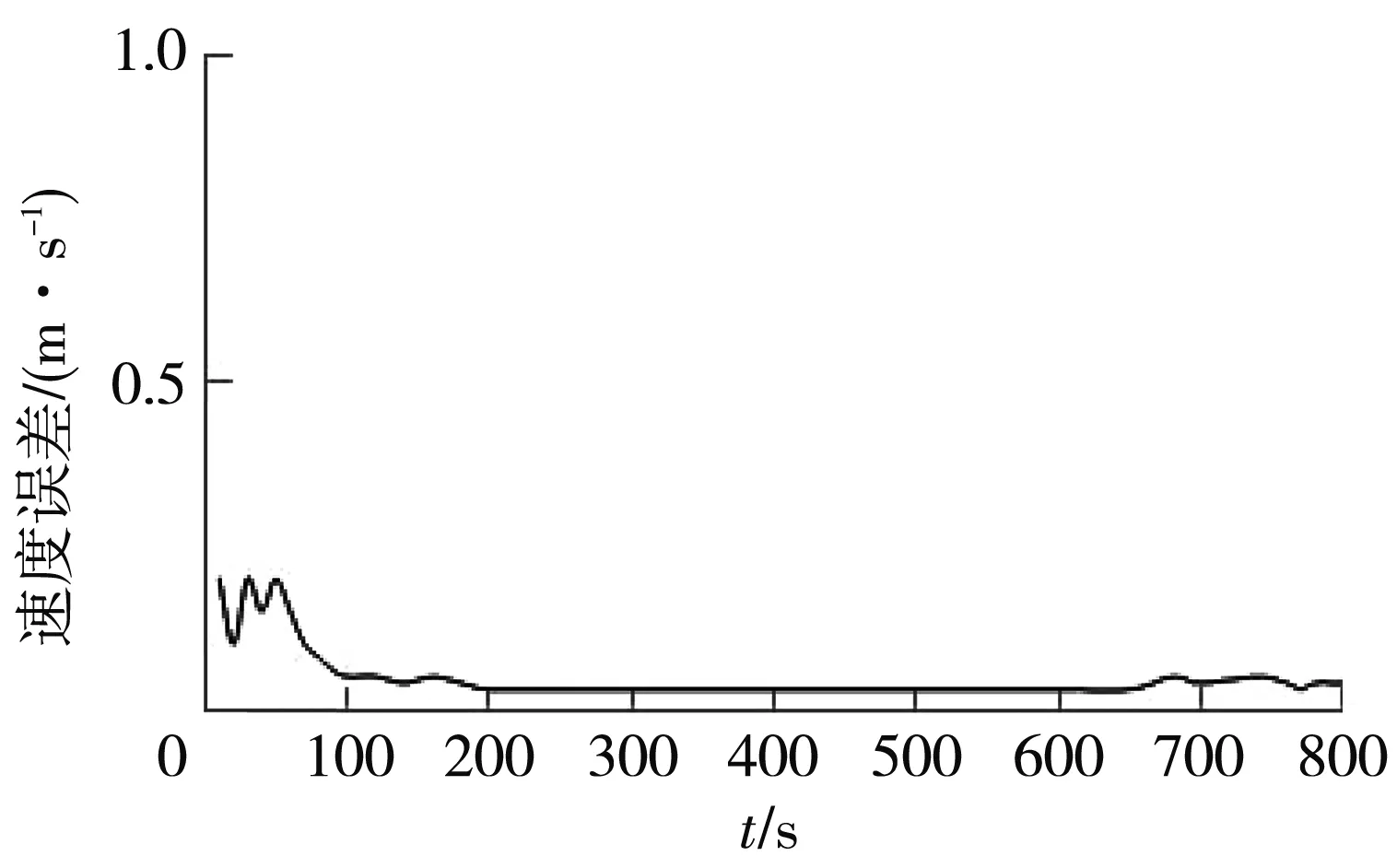
(a) 东向

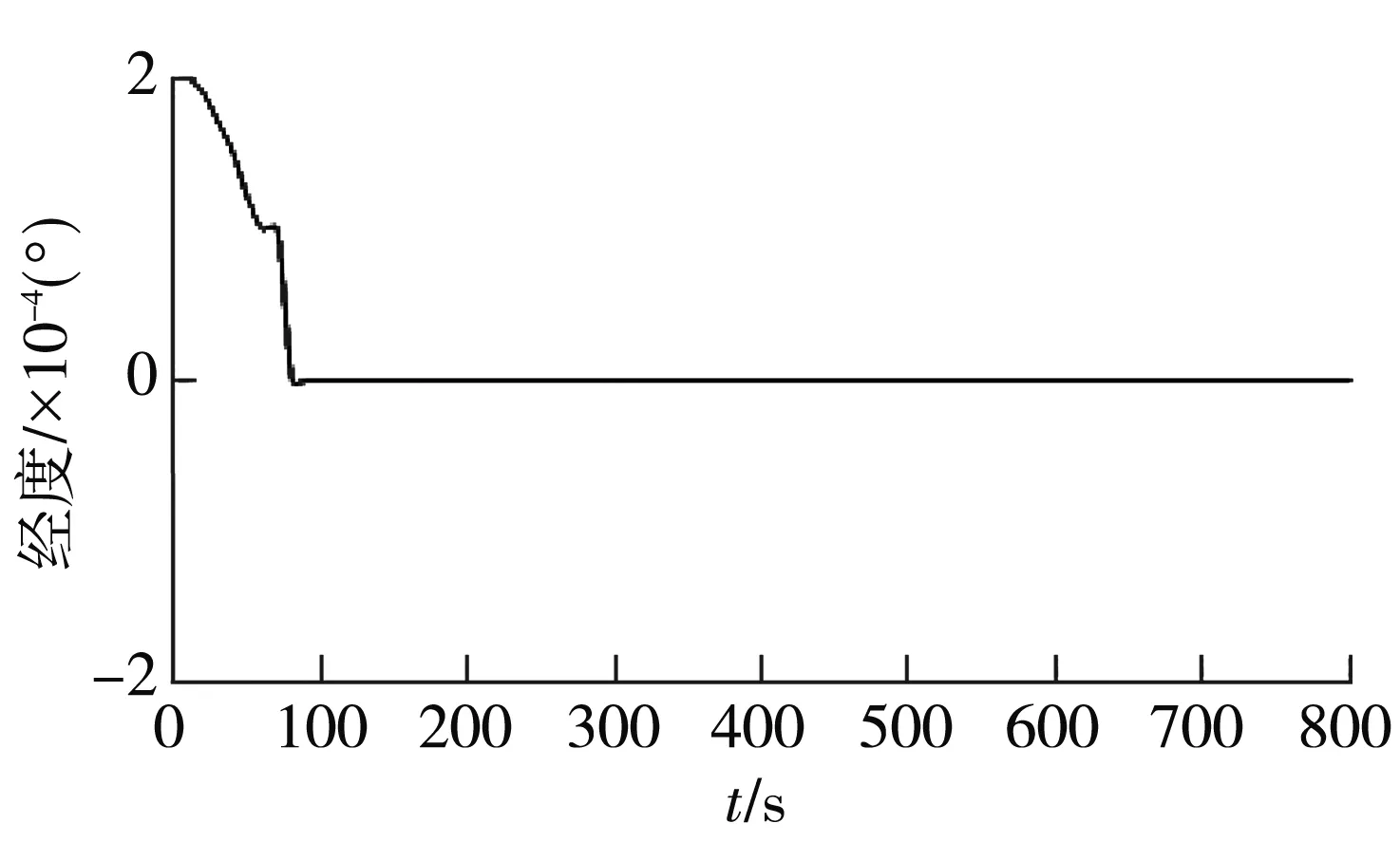
(a) 经度方向

表4为卡尔曼滤波估计的速度误差和位置误差在500 s时各个状态量的估计精度.

表4 状态量的估计精度Tab.4 Estimation accuracy of state variables

表5为卡尔曼滤波估计的误差补偿量修正误差后组合导航系统在500 s时各个状态量的估计精度.

表5 修正误差后的估计精度Tab.5 Estimation accuracy after error correction

由表4和表5可以看出，通过卡尔曼滤波估计的误差补偿量修正误差后，卡尔曼滤波趋于收敛，各个状态量的精度得到明显提升，组合导航系统使得每个状态量的估计误差得到很大改善，组合导航系统精度的可靠性得到进一步提升.

4 结 语

本文对GNSS与惯性导航组合系统在复杂环境下的定位原理进行了分析，并在不同环境下进行了实验，相比于惯性导航系统，组合导航系统在信号失锁的复杂环境下的定位定姿精度得到较大提升，该组合导航系统能够提供更加全面的导航信息.根据驾驶人考试在复杂环境下的应用需求，GNSS与惯性导航组合系统在复杂环境下的定位研究对推动驾驶人考试向智能化方向的发展具有重要意义，将为机动车驾驶人考试系统的推广应用提供理论和技术支撑.