非线性随机分数阶积分微分方程半隐式欧拉解的收敛性和稳定性
2021-02-25李晓卫贾宏恩
李晓卫,贾宏恩,郭 平
(太原理工大学 数学学院,山西 太原 030024)
0 引 言
积分微分方程是现代数学的重要分支,是人们解决各种实际问题的有效工具,它广泛应用于几何、力学、物理、电子技术、自动控制、航天、生命科学等领域,如反应堆动力学[1]、种群动态[2]和分层介质中的波传播[3],并且随着现实生活中的许多随机因素(如噪声等)被考虑进来,随机积分微分方程引起了国内外众多学者的关注与研究.
在现有研究中,随机积分微分方程被应用于随机力驱动的粘弹性结构构件的力学行为[4]、期权定价[5]及人口增长模型中[6].此外,一些学者证明了随机积分微分方程解的存在性、唯一性和稳定性[7-10].但在许多情况下,随机积分微分方程的精确解很难找到,因此,寻找求解此类方程近似解的数值方法引起了许多学者的关注.如,对于具有乘性噪声的随机微分方程,Tocino A等[11]提出了一种二阶显式RungeKutta格式,对于具有恒定扩散系数的标量方程,还得到了两种三阶RungeKutta格式;Babuska I等[12]采用蒙特卡罗Galerkin法和随机Galerkin有限元方法求解随机扩散和载荷系数的随机线性椭圆偏微分方程,当采用少量随机参数描述噪声时,随机Galerkin法为首选方法;Maleknejad K等[13]利用块脉冲函数求解随机沃尔泰拉积分方程,得到了精度较高的近似解.
随着分数阶微积分的发展,分数阶积分微分方程出现在信号处理的统计力学领域[14-16].目前,越来越多的研究者对随机分数阶积分微分方程进行了深入研究,探讨了此类方程解的存在性、唯一性和稳定性[17-18].而且,研究人员还研究了一些数值格式,并对这些数值格式的性质进行了探讨,如利用谱配置方法、欧拉方法以及径向基方法求解该类方程,并讨论了这些方法的性质[19-21].此外,Faedo-Galerkin方法、Legendre小波方法以及对应的收敛性也被研究和证明[22-23].
半隐式欧拉格式已被用于多种方程中,如随机受电弓方程和随机微分延迟方程[24-25],其精确解的稳定性已被证明[26].本文主要目的是给出随机分数阶积分微分方程的半隐式欧拉格式的收敛性分析和相应离散数值解的稳定性分析.
本文给出了一些必要的符号与准备,以及与原始方程对应的随机沃尔泰拉积分方程;分析了随机分数阶积分微分方程的半隐式欧拉格式的收敛性与收敛阶;给出了半隐式欧拉格式数值解的稳定性;最后通过数值算例验证了本文的理论分析.
1 符号与准备工作

考虑以下d维非线性随机分数阶积分微分方程


t∈[0,T],y(0)=y0,
(1)
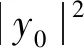
定义1 对函数f∶[0,+∞)→Rd的α阶Riemann-Liouvile 分数阶积分算子定义如下
α>0且I0f(t)=f(t),其中Γ(α)为Gamma函数,

定义2 对于函数f∈Cγ([0,+∞))的α阶Caputo导数可以记作
式中:γ-1<α<γ,γ∈N+.
由富比尼定理,式(1)可转化为以下随机沃尔泰拉积分方程(这两个方程的具体转化可参考文献[18])


(2)
其中
t∈[0,T],y(0)=y0,
i=1,2.
假设1 对于任意(t,s)∈Q,k1(t,s,0)与k2(t,s,0)是连续有界的函数,且存在正常数li,i=1,…,4,使得Ø,kj满足如下条件
|Ø(t1)-Ø(t2)|≤l1|t1-t2|,
|kj(t1,s,y)-kj(t2,s,y)|≤l2(1+|y|)|t1-t2|,
|kj(t,s1,y)-kj(t,s2,y)|≤l3(1+|y|)|s1-s2|,
对任意t,t1,t2,s,s1,s2∈[0,T],y,y1,y2∈Rd,j=1,2均成立.
在假设1的条件下,得到以下定理[18].
定理1 存在正常数Li,i=1,…,5,使得Φ(t),Kj(j=1,2)满足以下条件
|Φ(t1)-Φ(t2)|≤L1|t1-t2|,
|Kj(t1,s,y)-Kj(t2,s,y)|≤L2(1+|y|)|t1-t2|,
|Kj(t,s1,y)-Kj(t,s2,y)|≤L3(1+|y|)|s1-s2|,

|Kj(t,s,y1)-Kj(t,s,y2)|≤L5|y1-y2|,
对任意t1,t2∈[0,T],s1,s2∈[0,T],t,s∈[0,T],y∈Rd均成立.
下文中C代表一个任意的正常数.
2 半隐式欧拉格式的收敛性与收敛阶
精确解的存在性、唯一性和稳定性已在一些文献中有研究[18].本节讨论半隐式欧拉方法的收敛性与收敛阶.
首先,将整个时间区间分割为N个小区间,对于N≥1,令h=T/N,tn=nh,对于n=0,1,2,…,N,当t=tn+1时,


因此,定义

(3)


(4)

(5)
则得到以下半隐式欧拉格式

(6)
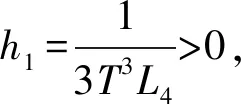

证明由式(3)和基本不等式,有

对上述不等式两端同时取期望,有

则得到
由离散Gronwall不等式
1+E(|Yn+1|2)≤
及Y(t)的连续性,得到
引理2 假定满足假设1,在h 证明对于任意的t∈[0,T],存在一个整数n使得t∈[tn,tn+1),由式(4)~式(6),得到 Y(t)-Y1(t)=Y(t)-Yn=Φ(t)-Φ(tn)+ 再由基本不等式,Cauchy-Schwartz不等式和It等距,得 同理, 再由基本不等式,Cauchy-Schwartz不等式和It等距,得 CL4h3≤Ch2. 定理2 在引理1的假设下,存在一个与h无关的正常数M使得 E(|y(t)-Y(t)|2)≤Mh2, 对任何t∈[0,T]均成立. 证明用式(2)减去式(6),并由基本不等式,Cauchy-Schwartz不等式和It等距,得 对上述6项分别进行处理得到 采用同样的处理方式,得到 那么 本节在假设1的条件下研究式(6)的数值解的稳定性. 定义3 设{Yn+1}n≥1为式(6)具有初始解ξ对应的解,{Xn+1}n≥1为式(6)对应初始值为λ的另一个解.对于任意的ε>0,存在一个正常数δ>0使得当E|ξ-λ|2<δ时,有 成立,即式(6)的解是均方稳定的. 证明由式(2)得 y(t)-x(t)=η-φ+ 对上式两端同时取期望,得 再由Gronwall不等式得 E|y(t)-x(t)|2≤ε. 定理4 设{Yn+1}n≥1,{Xn+1}n≥1分别为式(6) 对应于初始值ξ和λ的数值解,那么如果假设1成立,则式(6)的数值解就是均方稳定的. 证明由式(3)得到 对上述不等式两侧同时取期望,得 则 再由离散Gronwall不等式得 E|Yn+1-Xn+1|2≤ 因此,对任何的ε>0,存在一个正常数δ>0,当E|ξ-λ|2<δ时,有 E|Yn+1-Xn+1|2<ε 成立. 本节给出一个数值算例以验证随机分数阶积分微分方程半隐式欧拉方法的收敛率.类似于文献[18],使用样本均值逼近期望,更准确地说,使用以下表达衡量在最后时刻tN上的均方误差. 式中:y(i)(tN)和Y(i)(tN)分别为精确解与数值解. 例1 考虑1维随机分数阶积分微分方程且γ=1, 式中:t∈[0,1],且初始值y(0)=0. 注意到函数Ø,k1,k2均满足先前的假设条件,且将在时间步长为h=2-11下的数值解作为随机分数阶积分方程的精确解.在相同布朗路径上任意取3个不同的时间步长,即h=2-6,2-7,2-8,并分别求得其半隐式欧拉格式的数值解及相应的误差ε,相关结果如图1所示. 图1 例1中半隐式欧拉格式的均方误差Fig.1 Mean square error of semi-implicit euler scheme in example 1 当α=0.45与α=0.65时,图像斜率接近于1,即半隐式欧拉方法的一阶收敛率得到验证.3 半隐式欧拉格式的稳定性




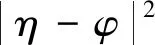



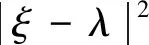
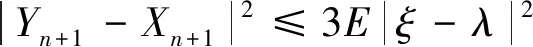

4 数值算例


