基于自然梯度的概率主组件分析在线学习算法

2021-02-25陈亚瑞秦智飞

天津科技大学学报 2021年1期

陈亚瑞，秦智飞

(天津科技大学人工智能学院，天津 300457)

数据降维[1]是指将高维样本数据通过线性或者是非线性变换映射到低维空间，获得高维数据在低维空间的一种表示.近年来，数据降维在众多领域变得越来越重要，高维的数据通过数据降维可以去除高维空间中不相关或者不重要的属性，减轻维数灾难，能够对数据的分类、压缩以及可视化带来良好效果.目前常用的降维方法有线性判别分析[2](linear discriminant analysis，LDA)、局部线性嵌入[3](locally linear embedding，LLE)、拉普拉斯特征映射[3](laplacian eigenmaps，LE)以及主组件分析[4-5](principal component analysis，PCA).LDA 是一种属于有监督学习降维技术，基本原理是使得投影之后的每一种类别数据的投影点尽可能接近，而不同类别数据的类别中心之间的距离尽可能大.LDA 在降维过程中可以使用类别的先验知识经验，但是LDA 不适合对非高斯样本分布进行降维，并且最多只能降到类别数减1 的维度.LLE 属于流形学[6](manifold learning)的一种.它将高维数据投影到低维空间中，并保持数据点之间的局部线性关系，其核心思想是每个点都可以由与它相近的多个点的线性组合近似，投影到低维空间之后要保持这种线性重构关系，并且有相同的重构系数.LLE 算法归结为稀疏矩阵[1]特征分解，计算复杂度相对较小，实现容易，但是算法对最近邻样本数的选择敏感，不同的最近邻数对最后的降维结果有很大影响.LLE 是用局部的角度去构建数据之间的关系，它的直观思想是希望相互间有关系的点(在图中相连的点)在降维后的空间中尽可能靠近，可以反映出数据内在的流形结构，但是局部特征保留特性使得它对孤立点和噪声不敏感.PCA 的主要思想是将n 维特征映射到k 维上，这k 维是全新的正交特征，也被称为主组件，是在原有n 维特征的基础上重新构造出来的k 维特征，消除了特征之间的多重共线性.通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵特征值的特征向量，选择特征值最大(即方差最大)的k 个特征所对应的特征向量组成的矩阵.这样就可以将数据矩阵转换到新的空间当中，实现数据特征的降维.但是PCA 在求解时需要计算数据的协方差矩阵，过程较为繁琐.概率主组件分析[7-9](probabilistic principal component analysis，PPCA)是从概率角度理解PCA，将PCA 纳入生成式框架，与传统的PCA 相比，PPCA 属于隐变量模型[10]，可以使用期望最大化[11](expectation maximization，EM)算法求解，避免了计算数据协方差矩阵.概率模型与EM 的结合能够处理数据集里的缺失值问题.PPCA 也可以用一种生成式的方式运行，生成新的样本.但是通过传统EM 算法求解PPCA 模型时会存在参数更新过慢的问题.

因此，本文首先介绍PPCA，针对PPCA 存在的问题提出基于自然梯度的概率主组件分析在线学习算法，结合实验验证该算法的有效性.

1 PPCA及EM算法

1.1 概率主组件分析(PPCA)

对于生成模型[12]p(x,z)=p (z) p(x|z)，其中x 表示观测向量，z 表示连续隐向量，p (z)表示隐向量先验概率分布，一般情况下先验概率分布为p (z)=N(z| 0,I)，p (x | z)表示条件概率分布.在生成模型结构下，观测样本 xi的生成过程如下：首先从隐变量先验分布 p (z)中随机生成一个隐向量样本 zi，然后根据条件概率分布 p (x | z)生成样本 xi.生成过程的概率表示形式为

生成模型 p(x,z)=p (z) p(x|z)对应的概率图模型形式如图1 所示，其中白色节点表示隐向量，黑色节点表示观测向量，节点之间的边表示变量之间的依赖关系.

图1 生成模型Fig.1 Generating models

概率主组件分析是生成模型的一种特殊形式，其中D 维观测变量x 由M 维隐变量z 的一个线性变换附加一个高斯噪声[13]定义，即

其中W 表示RD×M维的一个参数矩阵，ε 表示D 维零均值高斯分布的噪声变量，ε～ N(0,δ2I).

PPCA 模型的观测样本 xi的生成过程如下：首先从隐变量先验分布 p (z)中随机生成一个样本 zi，然后根据条件概率分布 p (x|z)生成样本 xi，即

对于观测数据集X={ x1,…,xN}，其中N 表示观测样本的个数，Z={ z1,…,zN}为对应的隐变量据集.PPCA 的学习任务是通过观测数据X={ x1,…,xN}学习模型(4)中的参数W、δ2和µ.

1.2 EM算法

EM 算法是求解隐变量模型最大似然问题的经典方法，其基本思想是通过 E(Expectation)步和M(Maximization)步两步不断迭代更新模型参数.其中 E 步是通过对完备数据集的对数似然函数ln p( X,Z | θ)求关于隐变量后验概率分布p (Z | X,θold)的期望，此步骤的目的是通过隐量后验概率分布处理隐变量.M 步是对于在E 步中的完备数据集对数似然函数的期望进行最大化处理，更新模型参数.

对于PPCA 模型，完备数据集的对数似然函数为

PPCA 模型采用EM 算法迭代计算模型参数.

E 步：对ln p (X,Z | θ)求关于p (Z | X,θold)的期望，即

其中计算E[ zn]和是该步骤的关键.根据后验概率分布计算可得

其中M=WTW +δ2I .

M 步：是最大化E[ln p (X,Z | μ, W,δ2)]更新模型参数

进一步求解可得

PPCA 模型EM 算法如下：

1.3 PPCA算法存在的问题

根据PPCA 模型的EM 算法描述，在进行一次参数更新的时候，需要首先计算出所有样本的Ε[ zn]和，然后再更新模型参数Wnew和该算法最大问题是每更新一次参数需要计算所有样本的隐变量后验概率分布的期望，会导致计算过于复杂，参数更新太慢；同时算法很难扩展到大规模数据集，因为每一次算法更新时都需要遍历整个数据集是不现实的.进一步，当数据量不断增加时，需要采用增量学习[14]算法，随着数据量增加不断提升算法的性能.基于以上问题，本文提出基于自然梯度的概率主组件分析在线学习[15]算法.

2 自然梯度

梯度上升方法[16]是求解优化问题的重要方法，它通过沿着目标函数梯度的方向进行参数迭代更新，求解最优化问题.在欧氏空间中，函数梯度方向是变化最快的方向，也是参数更新的最优方向.但是当优化的参数是概率分布时，欧氏距离不能有效地度量概率分布之间的距离.对称KL 散度[17](KL divergence)是度量两个概率分布之间相似性的一种度量方式，数学表述为

欧氏梯度是欧氏空间中上升最快的方向，而自然梯度[18]是黎曼空间(该空间采用对称KL 散度度量局部距离)内上升最快的方向.对于目标函数f(λ)，它的自然梯度为

3 本文算法

对于PPCA 模型的EM 优化算法，其中的最大化问题maxE[ln p (X,Z | μ, W,δ2)]，采用自然梯度上升方法求解该优化问题.根据自然梯度(式(13))及平均值场[7](mean field)理论可知

可以得到自然梯度具有以下的简单形式

在传统的PPCA 的EM 算法中，每一次参数的迭代更新都需要计算所有样本的后验概率分布，会使得算法的性能变得很差.在基于自然梯度的概率主组件分析在线学习算法中，使用单个样本对参数进行局部的更新，并在参数的更新时引入自然梯度.

对于单样本 xn，首先是计算样本所对应的隐变量后验分布

此时根据梯度下降算法，更新模型参数

基于自然梯度的概率主组件分析在线学习算法如下：

4 实验分析

本节在5 个数据集下设计一组对比实验，在不同训练样本个数下设计一组在线学习过程实验以及在MNIST 数据集下设计一组生成样本数据实验，分析实验结果，证明本文提出算法的有效性.

4.1 实验环境

本实验选用了5 个数据集，包括MNIST 数据集，Fashion-MNIST 数据集和 3 个 UCI 数据集(HOP、SDD、AREM).其中：MNIST 数据集为手写数字数据集，共有10 类；Fashion_MNIST 数据集包含有10 类不同商品的图片；HOP、SDD 及AREM 数据集是进行过特征提取后的数据集.数据集具体信息见表1.

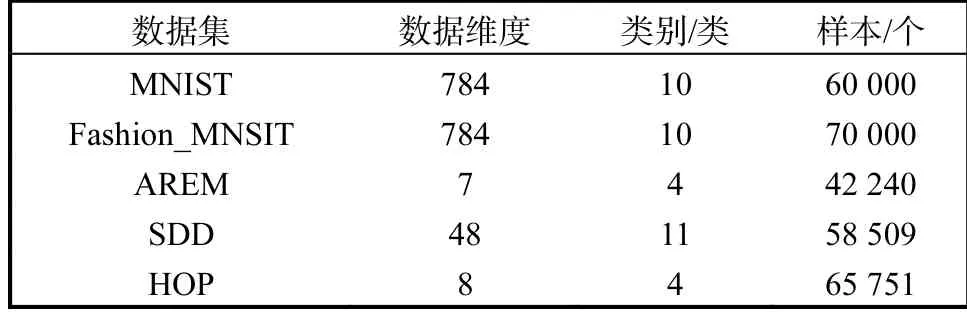
表1 数据集信息Tab.1 Data set information

实验平台信息如下：GPU 采用GTX1080，CPU采用i7-8700@3.30 Hz，运行内存为16 GB，操作系统Windows 7 旗舰版，运行平台工具python3.6.

4.2 实验设计

设计3 组实验.实验1(在线学习过程实验)：在基于自然梯度的概率主组件分析在线学习算法中，依次使用递增的训练样本个数对模型进行训练，比较分类正确率.实验2(精度对比实验)：在5 个数据集下分别运行PPCA 的EM 算法和基于自然梯度的概率主组件分析在线学习算法，并对比分析了算法运行时间及其分类正确率.实验3(生成样本实验)：在基于自然梯度的概率主组件分析在线学习算法中，依次使用递增的训练样本个数对模型进行训练，在训练好的模型中使用随机生成的隐变量生成新的样本，比较生成数据的效果.

4.2.1 在线学习过程实验

在基于随机化近似的在线EM 算法中，依次使用5 000、10 000、20 000、30 000、40 000、＞40 000 个数据样本对EM 算法进行训练，在训练好的模型下对数据进行降维，并将降维后的数据按照表2 所示分为训练集和测试集，通过单隐层全连接神经网络进行分类，batch-size 为32，在学习率0.1，epoch 为100，得到分类正确比见表3.

表2 分类数据集Tab.2 Classified data set

表3 基于不同训练样本个数的分类正确比Tab.3 Classification accuracy ratio based on different training samples

4.2.2 精度对比实验

在数据集上分别运行PPCA 的EM 算法和在训练基于自然梯度的概率主组件分析在线学习算法时，由于内存的限制，每个数据集都随机选用30 000 个样本用于训练EM 算法，最大迭代次数设置为500.在训练好的模型中，将MNIST、Fashion_MNIST 的数据样本降到200 维，将HOP 数据集样本降到4 维，将AREM 数据集降到5 维，将SDD 数据集样本降到22 维.将降维之后的数据集按照表2 所示比例分为训练样本和测试样本，通过单隐层全连接神经网络进行分类，batch-size 为32，学习率0.1，epoch 为100，得到分类正确比见表4，算法的运行时间见表5.

表4 分类精度Tab.4 Classification accuracy

表5 算法运行时间Tab.5 Algorithm running time s

4.2.3 生成样本实验

在基于自然梯度的概率主组件分析在线学习算法中，依次使用 5 000、10 000、20 000、30 000、40 000、＞40 000 个MNIST 数据样本对算法进行训练，隐变量的维度设置为2，从均匀分布中随机生成隐变量z，利用概率生成模型生成新的样本，样本的清晰度比较如图2 所示.根据图2 对比结果可知，在基于自然梯度的概率主组件分析在线学习算法中，随着训练样本的增多，所生成的样本越来越清晰，生成效果越来越好.