基于机器学习的建筑能耗SVM 模型降阶分析与研究

赵绍东

(天津市轻工与食品工程机械装备集成设计与在线监控重点实验室，天津科技大学机械工程学院，天津 300222)

根据节能和绿色环保要求，需要对独栋建筑实际产生的能耗情况进行预测.进行预测时可以在给定的条件下随机选择多种形式各异的特征样本用于模型训练，这些特征包括取暖能耗、天气变化、制冷能耗、独栋建筑自身的能源分布、通气排风等.

机器学习的目的是将现实问题模型化，使计算机模拟或者无限地接近于人类的学习行为，并且能够在现有的既定条件下精确地给出机器学习效果.对现实问题的真实模型的逼近程度往往取决于所选取的数据样本的科学性和合理性，因此在选取分类函数和分类器的时候，尽量选取贴近于真实模型的、精简的、具有代表性的准确数据[1-2].由于影响建筑能耗数值大小的因素种类非常繁多，如建筑形式与围护结构、电器设备系统、气象条件、室内环境需求等，因此对建筑能耗数据样本的选取和计算复杂度变得异常困难，无形中增加了分类函数的复杂度和VC 维度(Vapnik-Chervonenkis dimension).正因如此，借助于支持向量机(SVM)算法对样本的维数处理和模型降阶的强大优势和特性，解决建筑能耗数据文本特征子集和模型训练等问题.

1 建筑能耗特征选择算法

特征选择(feature selection，FS)在机器学习研究领域一直被研究人员所青睐，受到了极大的关注.特征选择的目的是为了更好地选择出最有用的特征集，并且为相关的学习算法建立一个性能良好的预报器.为了更加有效地降低维度，需要减少或者去除那些不相关的特征.

在进行探索性数据分析和训练预测模型研究中，主成分分析法(principal components analysis，PCA)和核主成分分析法(kernel principal component analysis，KPCA)是目前被研究者较为认可的两种常规的方法.通常情况下，在原始的样本数据集中，抽象出来的各个变量之间会或多或少存在某种或者多种内在的联系，而PCA 的特点则是在某种程度上尽可能地减少或者削弱变量之间的这些相关性，尽可能地避免所选取的样本数据的“近亲繁殖性”和“一致性”.PCA 通过采用正交变换的方式有计划、分步骤地将变量间可能存在的一系列“相关”的特征动态地转变为一系列“不相关”的特征，即主成分.经过PCA 处理后，虽然新增了部分新特征，但是总的特征数量实际上发生了大幅度减少.KPCA 可以理解为PCA 的核心扩展，主要包含和涉及了非线性主成分的核方法，并且能够在既定变量特征值范围内有效地获得原始变量之间的高阶相关性和潜在的新特征.

由于建筑能耗特征选择方面的研究较少且复杂性较高，因此本文在进行特征选择过程中主要采用两种方式：其一，根据每个特征与目标之间的相关系数对特征进行排序；其二，对每个特征分配权值，然后利用梯度上升进行特征权值的矢量评估.

2 SVM算法模型

SVM 算法是由Vapnik 等在数理统计方法和概率学习理论的基础上，针对线性分类器设计的最佳准则，适时提出的一种支持向量机机器学习方法[3-4].SVM 算法的主要特征是可以在线性不可分的情况下，通过精准地采用非线性映射算法成功地将低维输入空间线性不可分的样本动态地转化为高维特征空间，并且在理论意义上使其能够线性可分，在实际应用中实现将高维特征空间在给定条件下，通过采用线性算法的方式对随机抽取样本的非线性特征按照约定规则进行线性分析.该算法的特点是在应用结构风险最小化理论的基础上，按照给定的算法规则构造特征空间中可能存在的最优超平面，从而使抽象整理分析所得的学习器具有全局最优化的显著特点和优势.

在进行样本空间特征的非线性研究时，有时可以在特定的场景下，通过采用“非线性交换”的方式精准地转化为该场景下的某个高维空间中的线性问题，并且在转化的变换空间内按照既定的规则方法求解出对应的最优分类超平面[5-6].这种变换在真正的实现过程中具有一定的复杂性，因此可以采用寻找最优目标函数或者分类函数的方式对其进行逐步分析.例如，可以假定训练样本之间的内积运算为(x ⋅ xi)，设存在一种非线性映射函数Φ：Rd→ H，其中d 为维度向量，H 为高维特征空间.该函数可以成功地将输入空间的样本按照给定的规则动态地映射到高维(可能是无穷维)的特征空间H 中，当在特征空间H 中构造最优超平面时，训练算法仅使用空间中的点积，即Φ(xi)·Φ(xj)，而无需考虑单独的Φ(xi).因此，如果能够在合理范围内找到一个函数K，使其能够满足式(1)即可.

这样在高维空间实际上只需进行内积运算，而这种内积运算是可以用原空间中的函数实现的，甚至没有必要知道变换中的形式.根据泛函的有关理论，只要一种核函数 K (xi⋅ xj)满足Mercer 条件，它就对应某一变换空间中的内积.因此，在最优超平面中采用适当的核函数 K (xi⋅ xj)就可以实现某一非线性变换后的线性分类，而计算复杂度却没有增加.此时目标函数变为

而相应的分类函数也变为

算法的其他条件不变，这就是SVM.选择满足Mercer 条件的不同内积核函数，就构造了不同的SVM，这样也就形成了不同的算法.目前研究最多的核函数主要有3 类：

(1)多项式核函数

其中q 是所用多项式的阶次，所得到的是q 阶多项式分类器.

(2)径向基函数(RBF)

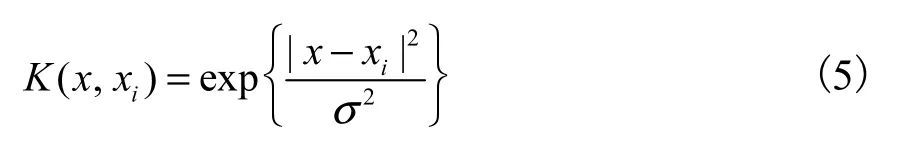
所得的SVM 是一种径向基分类器.它与传统径向基函数方法的基本区别是，这里每一个基函数的中心对应于一个支持向量.

(3)S 形核函数

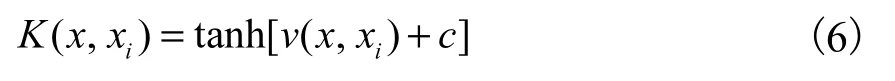
这时的SVM 算法中包含了一个隐层的多层感知器网络，网络的权值、网络的隐层结点数是由算法自动确定的，而不像传统的感知器网络那样由人凭借经验确定.此外，该算法不存在困扰神经网络的局部极小点的问题.

综合比较上述几种常用的核函数，鉴于建筑能耗数据样本特征的独特性和复杂性，本文对较为常用的多项式核函数和RBF 核函数进行对比研究，通过进行实验训练的方式，比较建筑能耗数据样本特征集的选择和预测分析，启发性地给出各个核函数在建筑能耗样本特征集的适用程度.

3 独栋建筑能耗的模型降阶

3.1 实验方法

在采用实验的方法进行建筑能耗样本集选取和比较分析过程中，选用相对具有代表性的特征子集对天津科技大学21#建筑能耗数据样本进行对应的统计模型训练.鉴于选取的样本集特征数目对于SVM训练过程中产生的计算成本影响相对较小，因此在实验的过程中只需考虑特征得分和选择方法的评价即可，同时将实验关注点集中在以下两个方面.

一是所选的特征应当具有唯一性和代表性，尤其对于预报器而言更加应该关注该特征的实效性，也可以通俗地理解为在特征选择完成后，模型的泛化误差必须控制在合理的范围之内[7-8].为了达到这种目的，必须在给定的目标中精确地加入高效率的特征选择算法，并且需要在一定程度上选择具有高排名或者较高得分的特征.

二是尽可能地确保在实验初期所选择的特征在日常的建筑能耗实践中具有普遍性和易获取性.对于具体的能量数据而言，通常情况下是可以采用从现实世界进行测量和调查中顺利获取的.例如，通过查询相关的建筑规划和建筑资料文件收集所需的数据信息，并且从每个给定的观测值中动态地选择最佳的特征值.但是，在实际的操作中很难得到有效、精简、实时、准确的数据，因此，在实验过程中尽量地减少不必要的或者对实验结果影响较小的特征[9-10].

以上两方面是本次实验采取的两个主要评价标准，同时选取两种方法来评价特征的有用性.方法一为在模型训练前就对原始数据进行预处理，并且根据每个特征与目标之间的相关系统对特征进行排序；方法二为回归梯度指导特征选择方法，首先对每一个特征分配一个权值，然后通过梯度上升等计算方法评估所有特征的权值矢量.目标数据集为正常的天津科技大学21#建筑在工作日所产生的建筑能耗，具体数据信息见表1.

表1 两种选择方法评估的特征得分Tab.1 Characteristic score of two selection methods

3.2 独栋建筑能耗数据仿真

为了使独栋建筑能耗研究更加的具体化，选取天津科技大学21#建筑作为研究对象，并且在供暖季节(2018 年11 月1 日至2019 年3 月31 日)对其进行仿真.对21#建筑特征描述见表2.为了表示21#建筑的更多细节特征，适当地提取该栋楼表面的材料，具体参数见表3.

由于研究对象选定的是供暖季节，因此该栋楼的主要能源消耗来自于研究对象室内的各个办公室和实验室的供热区域.为了方便本文实验数据的采集，可以假定该栋楼区域内的温度始终保持在一个平均的、恒定的值，同时还要考虑工作日的办公设施(如热水器、加湿器等)和正常的实验课程的开设所消耗的能源.对于楼宇内各个房间的墙壁，出于建筑材料热性能的考虑，可以设定为采用了如表3 所示的3 种建筑材料.21#建筑楼内的开启/关闭时间，以及楼内各个房间的设备设施运行时间为天津科技大学正常的教学办公时间.

表2 21#建筑特征描述Tab.2 Architectural characteristic description of 21#building

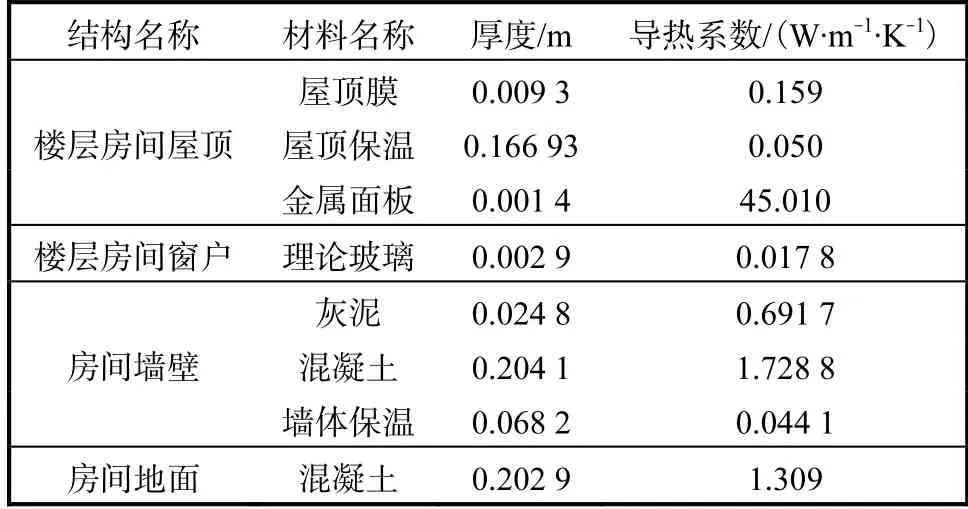
表3 仿真中用到的建筑材料Tab.3 Building materials used in simulation

将21#建筑楼的建筑能耗采用EnergyPlus 进行仿真处理，在仿真过程中提取时间序列数据，首先更新可变部分来使它具体到整栋楼宇，然后将它与稳定部分结合，产生EnergyPlus 最终的输入文件.这个过程一直重复到预先设定的所有建筑参数全部执行完成为止.为了对21#建筑的能耗仿真进行实例说明，选取11 月至12 月份的每小时电力能耗进行仿真实验，结果如图1 所示.

由图1 可以看出，设定这两个月的时间序列相同，均为30 d，其中紫色曲线代表11 月电力能耗，蓝色曲线代表12 月电力能耗.从图中的某些峰值点来看，每天的数值变化存在一定的差异性.

图1 21#建筑楼11月、12月每小时电力能耗仿真图Fig.1 Hourly power consumption simulation of 21#building in November and December

3.3 实验结果分析

通过从筛选出的实验数据集中按照评分等级进行区分，并且消除权值影响较小的特征，使之重新产生新的、精简的训练和测试数据集，在新生成的数据集基础上对该模型应用新的训练数据按照之前的操作进行重新训练，并将模型应用于测试数据进行预测.如此反复操作，最终得到如下结果：MSE 方法评价模型性能值为6.18×10-4，SCC 方法评价模型性能值为0.958.为了进一步发现和清楚展现在特征选择之前和之后模型性能的变化规律，以21#建筑的耗电量为例，在图2 中动态地绘制了21#建筑每日进行特征值选择后，日耗电量的测量值和预测值，并且在图3 中显示预测的相对误差范围.

图2 21#建筑每日耗电量的测量值和预测值Fig.2 Measured and predicted daily power consumption of 21# building

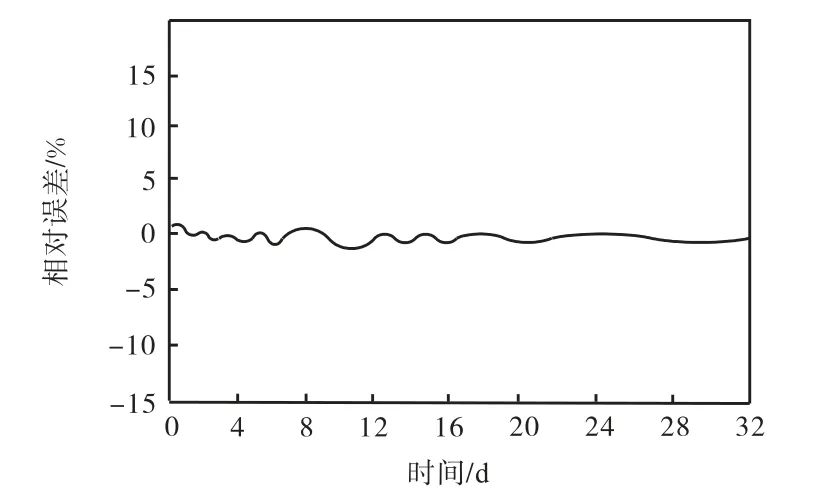
图3 预测的相对误差曲线图Fig.3 Predicted relative error curve

由于在特征重新进行选择后，剩余的特征数仅为8 个，这个数字相当于原始特征集中总体个数的1/2.但是，即便如此，与特征选择应用之前的数据结果相比，模型的预测效果和准确度能力依然保持较高水平，因此所选子集达到的效果可以认为是令人满意的，符合预期效果.

为了从实验的角度一步估算和评价所选的特征集是否能够达到优化状态，将其进行动态分组，并且整合成为4 个其他相互独立的子集(可参见表4 中的案例一至案例五).在案例二中，选择方法二单独评价下的顶部8 个特征，该操作的目的主旨在于在验证单一采取方法二是否能够在既定的条件下选择出最佳的特征集.在这种情况下，案例一忽略区内总热增益特征；案例二将选择的建筑周边室外空气密度、水管温度和建筑周边的区域平均气温换成室外相对湿度、风速和暖气出口温度；案例三将3 个选定的特征动态地换成其他3 个未选定的特征；案例四除了建筑周边区域内总热增益之外，所有选择的特征都用其他未选择的特征替换；案例五将两个得分最低的特征(人员数和建筑周边区域渗入量)从所选子集中动态地剔除.最终，基于以上5 种方案的考虑，相应地生成4 个新的数据集，同时加以训练和测试，并且对以上案例的每种情况重新训练模型，计算出不同特征集下模型性能的比较数据，计算结果见表4，其中NF为特征数，MSE(mean squared error)为均方误差法，SCC(squared correlation coefficient)为相关系数二次方法.

表4 不同特征集下模型性能比较Tab.4 Comparison of model performance under different feature sets

从表4 中的模型性能比较数据结果可以看出：本文所设计实验特征选择方法具有一定的合理性，对比结果较为显著，基本是可行有效的.比较分析可知，案例一中的模型性能从数据上显示具有一定的优越性；另外，具有RBF 核的SVR(support vector regression)模型较之其他具有更加稳定的性能，对所有4个数据子集总能获得较高的预测精度.

在天津科技大学21#建筑的特征集下模型性能比较的基础上，本文又引申设计了两个能耗数据集：第1 个数据集包括30 栋建筑；第2 个数据集包括60栋建筑.为了全面研究这两个数据集中特征选择针对SVR 模型产生的影响程度，引入两个核函数：RBF核函数和多项式核函数.由于所选的多栋建筑实验样本数据的特征值是在独栋建筑特征集的基础上，假定在相同建筑结构上的有限次累加，因此多栋建筑的特征选择将特征数从原来的17 个减少到12 个，这些数据集的MSE 和SCC 方法评价模型性能值见表5.

表5 具有两种核SVR对3个数据集的预测结果Tab.5 Two kernel of SVR predictions for three data sets

由表5 可知：对于30 栋建筑数据集来讲，MSE的值较之特征值重选之前有所增加，表明预测精度减小；然而，从SCC 的角度分析，具有RBF 核的模型性能与没有进行特征选择的情况所得的结果相对来说比较接近.

对于多项式核函数，当采用原始数据集进行对应的训练时，模型所达到的预测能力与RBF 核函数产生的效果基本相似.当采用特征选择后，模型性能在选取60 栋建筑能耗数据样本的实验环境下有了明显提高，但是，在选取30 栋建筑的环境下却出现了某种程度的降低.这种实验现象说明多项式核函数在某种意义或者环境下似乎没有RBF 核函数稳定，同时该现象也表明，当涉及实验环境采取的训练样本比较多时，本文所提出的特征选择方法在一定程度上可以提升模型的性能.

建筑能耗数据统计模型中特征选择同时也可以有效地减少训练时间.图4 展示了RBF 核函数的SVR 所消耗的训练时间比较，其中图中的时间级数呈对数形式.可以看出，特征选择后的训练时间较之特征选择前的训练时间相比有了一定程度的减少，提升了样本训练速度.

图4 特征选择前后RBF核函数训练时间对比Fig.4 Comparison of training time of RBF kernel function before and after feature selection

4 结语

本文为了有效地评估所提出的特征选择方法，首先由EnergyPlus 动态地生成3 个数据集，3 种数据集分别包括独栋建筑(以天津科技大学21#建筑为例)、30 栋建筑和60 栋建筑的时间序列下所产生的建筑能耗数据；然后假定将所开发的模型应用于实际建筑的能源需求预测，特征值根据操作中的可行性进行针对性的选择；最后给每一个特征赋予一定的分值，并且根据每个特征对预测的有用性进行分析和对比.根据实验分析，所选建筑能耗数据子集是可行的、有效的，并且获得了客观的预测结果和良好的模型性能.当涉及到的建筑能耗数据训练样本越多，模型性能效果越显著.在某些环境下，模型性能得到了明显的改善，例如，对于60 栋建筑能耗数据的预测，无论RBF 核函数，还是多项式核函数，模型的精度明显地提高，模型学习时间也有了一定程度减少.由于实验过程中需要估计更多的核函数参数，因此在下一步的研究中需要丰富和完善更加复杂的建筑能耗样本数据预处理工作.