幂零奇点的局部可积性及其分类

汪银姿,胡召平

(上海大学理学院, 上海 200444)

平面多项式微分系统的可积问题是微分方程定性理论的核心课题之一, 被刘一戎等[1]列为平面向量场的4 大经典问题之一. 尽管一般的系统都是不可积的, 但在研究数学模型时可积系统非常重要, 因为对一个可积系统进行扰动可以得到丰富的分支现象. 目前, 研究可积问题的成果相当多[2-14]. 另外, 退化奇点的分类也是微分方程定性理论的另一个重要课题. 韩茂安[15]对平面哈密顿系统的幂零奇点给出了一个有效的分类方法, 而这里的幂零奇点是一类特殊的退化奇点. 可见, 哈密顿系统只是一类特殊的可积系统, 目前也有相当多的学者研究哈密顿系统[16-22].

中心问题是另一个和可积性问题密切相关的经典问题, 也是同属于平面向量场理论中的4 大经典问题之一[1]. 所谓的中心问题是, 在什么条件下平面实多项式系统

以原点(0,0)为中心? 众所周知, 原点(0,0)为系统(1)的中心当且仅当具有如下形式的首次积分:

即函数F(x,y)满足方程

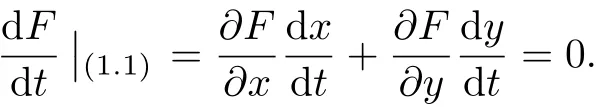
引入变换u=x+iy,v=, i dt=dτ, 并仍记τ为t, 则系统(1)变为如下复平面上的多项式微分系统:

因而, 中心问题等价于系统(2), 具有如下的首次积分:

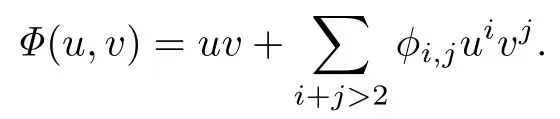
此时, 称原点为系统(2)的1:-1 共振中心.

进一步地, 该问题可以推广到如下更一般的复系统:

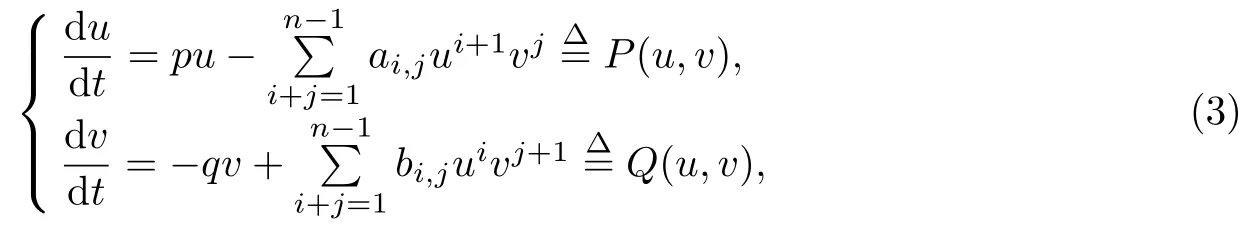
式中:p,q ∈N 且互素, 并将高次项的系数记为

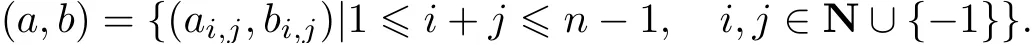
若系统(3)具有形式

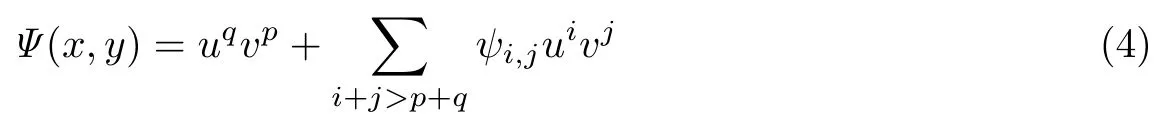
的首次积分, 则称系统(3)在原点局部可积, 亦称原点为系统(3)的p:-q共振中心.

由此可见, 上述可积问题可以看作是中心焦点问题的一个推广, 主要讨论实多项式系统的中心焦点和复多项式系统的p:-q共振中心. 而本工作将讨论幂零奇点的局部可积性. 幂零奇点是一类退化奇点, 比中心焦点的情形更复杂. 这里将讨论平面实系统

的局部可积性, 并在可积条件下讨论幂零奇点(0,0)的完全分类问题.

1 准备工作

1.1 局部可积性问题

系统(3)以原点为p:-q共振中心当且仅当系统具有形如系统(4)的首次积分. 因此,

即

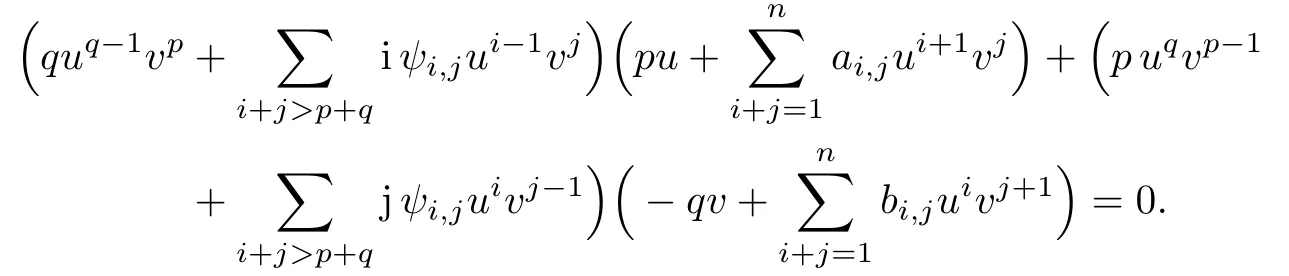
记gk1,k2为上式左端uk1+qvk2+p项的系数, 则有

若pk1-qk2=0, 且k1=kq, k2=kp, k ∈N, 则

多项式gkq,kp称为系统(3)的第k个可积量, 记作ik(a,b). 显然, 系统(3)可积当且仅当所有的可积量ik(a,b)均为0. 由所有的可积量生成的理想I=＜i1,i2,··· ,ik,··· ＞称为Bautin 理想, 而其簇类

称为系统(3)的可积簇. 因此,系统(3)可积的充要条件即为V. 进一步,记Ik=＜i1,i2,···,ik ＞,且Vk=V(Ik), 易知

由Hilbert 有限基定理可知, 存在有限的自然数N, 使得I=IN, 从而V=V(IN) =VN.这就使得通过得到有限可积量就找到系统可积的充要条件成为可能. 然而, 可积问题最大的障碍就在于如何得到尽可能多的可积量, 以及如何保证这些可积量是足够的. 为此, 通过Romanovski 等[13]给出的Singular 代数编程中的minAssGTZ 算法, 可以将这N个可积量构成的簇类分解为若干个不可约集C1,C2,··· ,Cm, 即

这样, 系统(3)可积的必要条件就是系数(a,b)至少包含在C1,C2,··· ,Cm中某个集合内.

接下来, 还需要证明上述条件急必要还是充分的, 即VN=C1∪C2∪···∪Cm ⊆V. 也就是说, 仅需要证明在每个条件Ck(1 ≤k≤m)下系统(3)是可积的, 即Ck ⊆V.

目前, 已有不少方法被用来证明系统(3)可积的充分性(如时间可逆性)、Darboux 首次积分法等. 在这里, 仅简略介绍Romanovski 等[13]给出的Darboux 首次积分法的几个结论.

定义1[13]对于系统(3), 若存在函数f(u,v)及多项式函数k(u,v), 使得

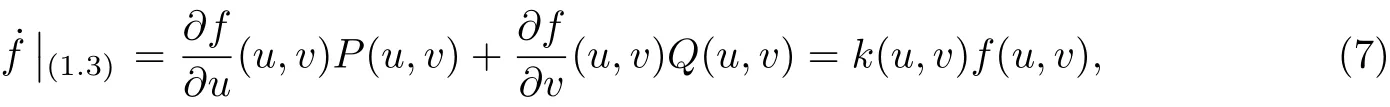
则称函数f(u,v)为系统(3)的一个Darboux 因子, 而k(u,v)称为对应的余因式.

为了构造系统(3)的一个Darboux 首次积分, 有如下的定理.

定理1[13]若系统(3)有Darboux 因子f1,f2,··· ,fm, 且对应的余因式k1,k2,··· ,km满足条件

则Φ=为系统(3)的一个Darboux 首次积分; 若满足

则系统(3)有一个Darboux 积分因子

故系统(3)可积.

由此不难看出, 研究多项式微分系统(3)的可积问题可以遵循如下步骤:

步骤1 利用Mathematica 等数学编程软件, 尽可能多地计算出系统(3)的前若干个可积量ik(a,b),k=1,2,··· ,N0;

步骤2 由minAssGTZ 算法将簇类VN0={(a,b)|i1(a,b) =i2(a,b) =···=iN0(a,b) =0}分解为若干不可约的集合C1,C2,··· ,Cm的并;

步骤3 在每个条件Ci下, 证明系统(3)是可积的,i=1,2,··· ,m.

1.2 幂零奇点的分类

在平面向量场理论中, 幂零奇点是指该奇点对应的线性近似系统的系数矩阵本身是非零矩阵而平方为零矩阵的情形. 显然, 幂零奇点是退化奇点的一个特殊情况. 此时, 该系数矩阵以0 为二重特征值, 对应的标准型矩阵为一个若当块. 而退化奇点在添加非线性项的情形下将变得非常复杂. 目前, 有不少关于退化奇点的讨论, 但给出完整分类结果的非常少, 仅有韩茂安[15]对平面哈密顿系统的幂零奇点提出了一个行之有效的方法, 并得到了完整的分类结果.

考虑平面多项式哈密顿系统

其对应的哈密顿函数为

易知Hyy(0,0) = 1. 由隐函数定理可知, 当|x|充分小时, 方程Hy(x,y) = 0 有唯一的解析解y=φ(x)=O(x2). 通过计算易得

其中

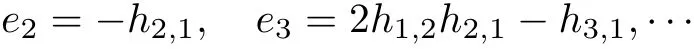
故将解y=φ(x)代入哈密顿函数H(x,y)并泰勒展开可得

其中

令k≥3 满足条件

则有如下的结论.

定理2[15]对于系统(8), 设系统(10)和(11)成立, 则

(i) 若k为奇数, 则原点为系统(8)的一个尖点;

(ii) 若k为偶数且hk ＜0, 则原点为系统(8)的一个鞍点;

(iii) 若k为偶数且hk ＞0, 则原点为系统(8)的一个中心.

定理3[15]对于系统(8), 设系统(10)和(11)成立. 则

(i) 当k=2m+1 时, 原点称为系统(8)的一个m阶幂零尖点;

(ii) 当k=2m+2 且hk ＞0 时, 原点称为系统(8)的一个m阶幂零中心;

(iii) 当k=2m+2 且hk ＜0 时, 原点称为系统(8)的一个m阶幂零鞍点.

2 几个推广的结果

考虑如下的平面实多项式微分系统

若系统(12)有如下的首次积分

则称系统(12)在原点是局部可积的. 此时, 有

通过计算可得

显然, 函数H(x,y)为系统(12)的首次积分当且仅当所有的ti,j=0 成立. 求解方程组ti,j=0,可以看出如下的项均必须为0:

类似地, 称ik(a,b)为系统(12)的第k个可积量.

如果找到了系统(12)的前N个可积量i1,i2,··· ,iN, 那么就找到了系统(12)可积的一个必要条件:

进一步地, 如果N足够大且V=VN, 就得到了系统(12)可积的充要条件V. 类似于第2 节中处理VN的方法, 并且关于可积充分性的结论对系统(12)仍然是成立的. 因此, 可遵循第2 节中的3 个步骤来研究系统(12)的局部可积性.

现在, 研究系统(12)在原点局部可积的条件下幂零奇点(0,0)的分类问题. 显然, 系统(12)有首次积分

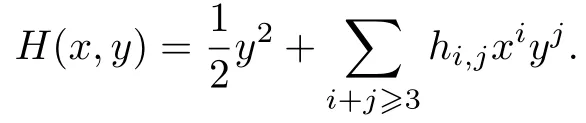
若存在满足条件μ(0,0)/=0 的函数μ(x,y), 使得

成立, 则μ(x,y)称为系统(12)的一个积分因子. 引入变换t=μ(x,y)τ, 系统(12)可化为如下的哈密顿系统

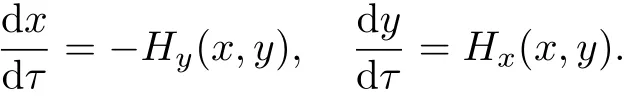
然而, 目前可积系统的积分因子μ(x,y)存在性问题仍然是一个公开的问题. 韩茂安[23]对系统(1)给出了一个积分因子μ(x,y)存在性的证明.

定理4[23]若系统(1)以原点为中心, 则存在解析函数H(x,y)=x2+y2+···, 且满足条件μ(0,0)/=0 的函数μ(x,y), 使得系统(1)可写为

对于原点为p:-q共振中心或幂零奇点的可积系统, 不能证明μ(x,y)的存在性, 但是也从未发现可积系统无积分因子的反例. 若找到了满足条件μ(0,0)/= 0 的积分因子μ(x,y), 则系统(12)在原点附近与对应的哈密顿系统是拓扑同构的. 因此, 可以由韩茂安[15]研究哈密顿系统幂零奇点的方法, 给出可积系统(12)的幂零奇点(0,0)的分类结果.

3 带幂零奇点的2 次系统

对于如下2 次系统

这里将讨论系统(13)在原点的局部可积性, 并在每个可积的条件下讨论幂零奇点(0,0)的完整分类情况.

3.1 可积条件

定理5系统(13)可积当且仅当下列条件之一成立:

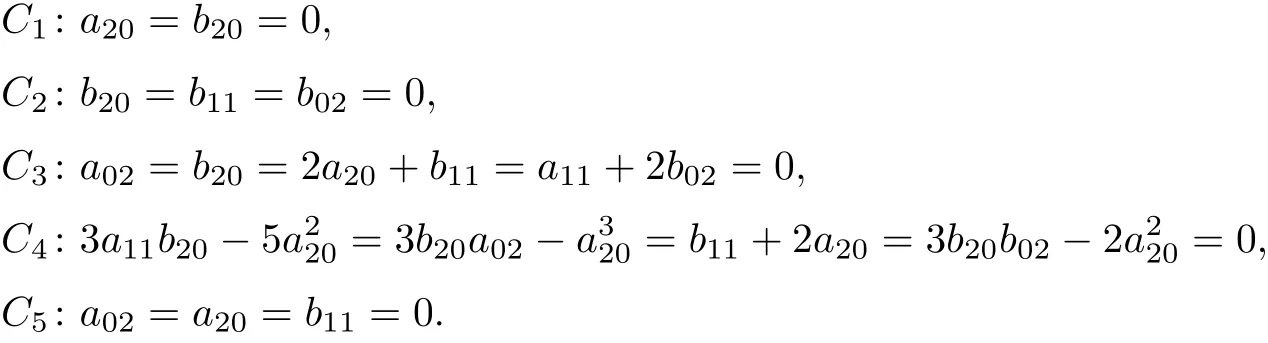
证明 首先证明必要性.

运用Mathematica 编程计算系统(13)的可积量, 易得i1=b20(2a20+b11). 由于计算比较复杂, 故分b20=0 和b20/=0 这2 种情况分别计算可积量. 得到了b20=0 情形下的前5 个可积量i1,i2,i3,i4,i5和b20/=0 情形下的前5 个可积量i*1,i*2,i*3,i*4,i*5如下:

由此可见,

这里,V(＜i1,i2,i3,i4,i5＞)和V(＜,1-λb20＞)各表示i1=i2=i3=i4=i5= 0 和= 0,b20/= 0 的解. 利用minAssGTZ 程序对V5进行不可约分解, 得到了5 个不可约集, 即分别满足定理中条件C1,C2,C3,C4和C5的解集, 仍记为C1,C2,C3,C4和C5, 从而得到

必要性得证.

下面证明充分性, 即C1∪C2∪C3∪C4∪C5=V5⊆V.

C1: 此时, 系统(13)可化为

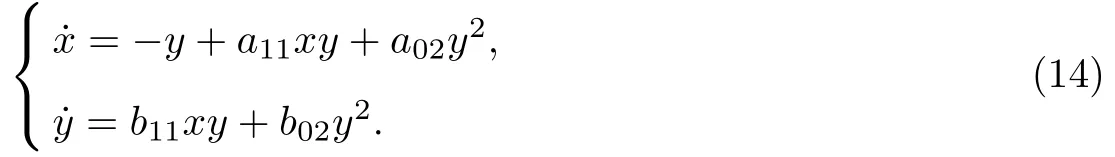
设系统(14)存在Darboux 因子f(x,y)和对应的余因式k(x,y)分别为

由定义1 有

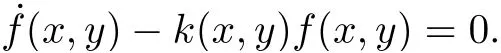
求解可得系统(14)有2 个Darboux 因子f1(x,y)=y和

对应的余因式分别为

而系统(14)的发散量为

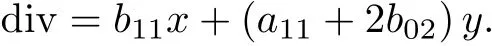
解方程

可得a1=a2=-1. 因此, 由定理1 可知系统(14)有积分因子

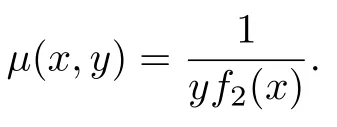
从而系统(14)可积.

C2: 此时, ˙y=0, 系统(13)显然可积.

C3: 此时, 系统(13)为哈密顿系统, 故必可积.

C4: 若b20= 0, 则为C3的情形. 故仅考虑b20/= 0 的情形. 不失一般性, 不妨设b20= 1,则系统(13)变为

系统(15)中的Darboux 因子和余因式分别为

由定理1, 可得系统(15)有首次积分

因此, 该系统可积.

C5: 此时, 系统(13)可以写为

该系统有Darboux 因子f(x,y)=1-a11x, 对应的余因式为k(x,y)=a11y.

另一方面, 系统(16)的发散量为(a11+2b02)y. 由定理1, 可得该系统有积分因子

故系统(16)可积.

综上所述, 有V=C1∪C2∪C3∪C4∪C5.

3.2 幂零奇点的分类

考虑系统(13)可积时相应的幂零奇点的分类情况. 显然, 条件C1或C2下系统的原点为非孤立奇点, 故不予考虑; 而条件C3下系统(13)为哈密顿系统

对应的哈密顿函数为

这是一个2 次哈密顿系统, 韩茂安[15]已经给出了该系统原点详细的分类情况.

对于条件C4和C5的情形, 有如下的结论.

定理6条件C4下的系统(13)为

此时, 原点必为尖点, 且阶数为1.

证明 由定理5 可知, 系统(17)有首次积分

从而可得系统(17)的一个积分因子

因此, 系统(17)等价于如下的哈密顿系统:

由隐函数定理可知, 当|x|充分小时方程Hy(x,y)=0 有唯一的解析解

式中,

因此,

由定理2 及3 可知, 原点必为1 阶尖点.

定理7条件C5下的系统(13)为

当b20/=0 时, 原点为1 阶尖点; 当b20=0 时, 原点为非孤立奇点.

证明 由定理13 可知, 系统(18)有积分因子

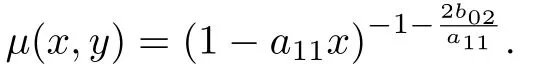
故系统(18)等价于如下的哈密顿系统:

其对应的哈密顿函数为

此时, 有φ(x)=0, 且

其中,

故当b20/=0 时,h3/=0, 原点为1 阶尖点; 当b20=0 时, 直线y=0 上所有的点均为奇点, 即原点为非孤立奇点.

4 含幂零奇点的3 次系统

考虑如下的3 次系统

对于系统(19)的局部可积性, 有如下的结论.

定理8系统(19)可积, 当且仅当下列条件之一成立:

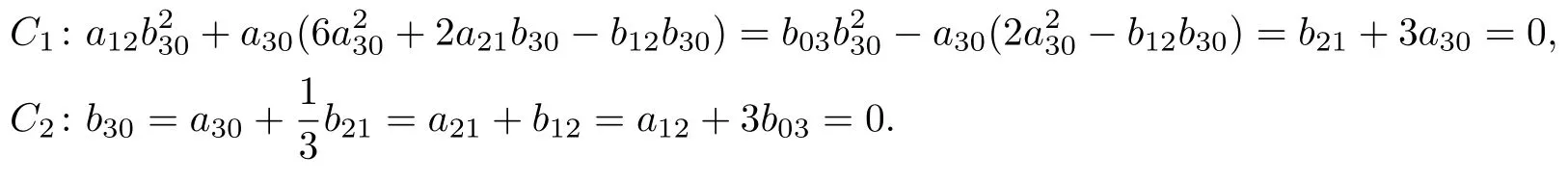
证明 首先证明必要性.

假设系统(19)有首次积分

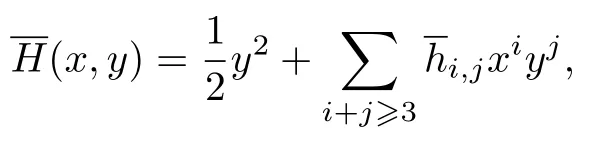
即

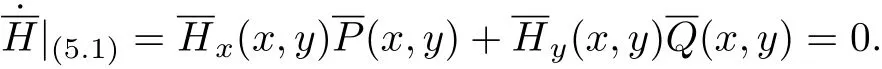
通过计算可知,

这样, 得到了系统(19)可积的一个必要条件为

利用minAssGTZ 程序对V5进行不可约分解, 得到了2 个不可约集, 分别满足C1和C2的解集,仍记为C1和C2. 因此,C1∪C2=V5⊇V. 必要性得证.

为了证明充分性, 即V5⊆V, 需要证明C1⊆V且C2⊆V.

C1: 若b30=0, 则a30=b21=0, 此时系统(19)显然可积.

当b30/=0 时, 有

因此, 系统(19)可化为

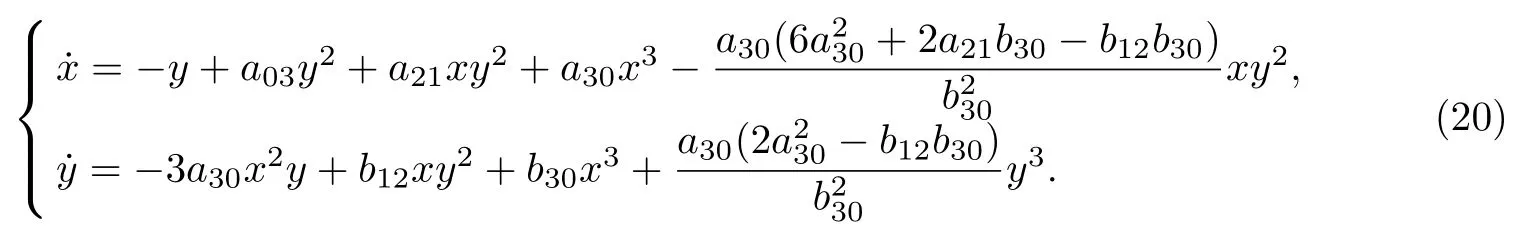
计算可得, 系统(20)有Darboux 因子

和

并且对应的余因式分别为

和

而系统(20)的发散量为

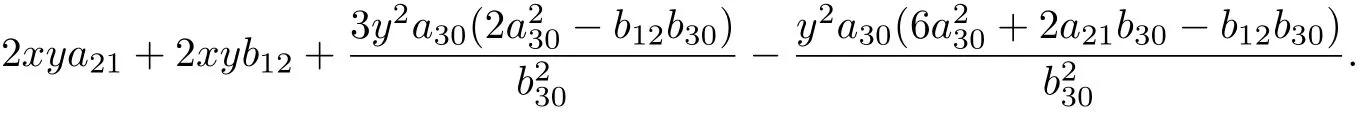
由定理1, 得到积分因子

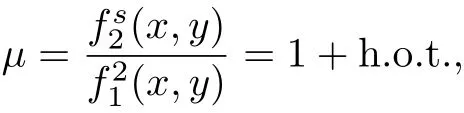
其中,

由定理1 可知, 系统(20)可积.

C2: 此时系统(19)为哈密顿系统, 显然可积.

最后, 考虑系统(19)在可积条件下幂零奇点(0,0)的分类情况. 条件C2下系统为哈密顿系统, 具体的分类结果已在文献[15]中给出. 而条件C1下有如下的结果.

定理9对于满足条件C1的系统(19), 当b30＞0 时, 原点为1 阶幂零中心; 当b30＜0 时,原点为1 阶幂零鞍点; 当b30=0时, 原点为非孤立奇点

证明 由定理8 可知, 当b30/=0 时系统(20)有积分因子

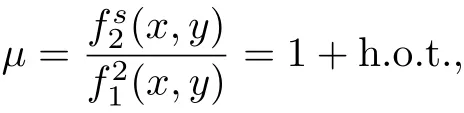
对应的哈密顿函数非常复杂, 但可以得到其泰勒展开式的前若干项:

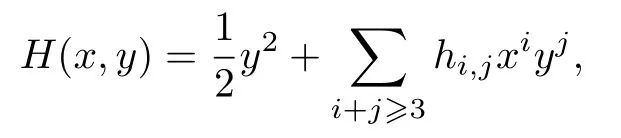
其中,

因此, 当b30＞0 时,h2=h3= 0,h4＞0, 原点为1 阶幂零中心; 当b30＜0 时,h2=h3=0,h4＜0, 原点为1 阶幂零鞍点; 当b30=0 时,a30=b21=0, 则直线y=0 上所有的点均为奇点, 即原点为非孤立奇点.