通过波函数单元探索化学键: DVMS 方法

刘 禹,李永乐,任 伟

(上海大学理学院量子与分子结构国际研究中心, 上海 200444)

1 化学键历史简介

化学键是描述分子结构、化学反应等化学现象的关键成分之一, 如何正确描述化学键, 在化学研究中具有举足轻重的地位. 人们对于化学键的探索, 最早可以追溯到公元前. 早在公元前410 年, 希腊哲学家德谟克利特(Democritus)将化学键假想为钩子的形状, 认为固体间的原子就是通过保持钩子形状连接在一起的[1]. 在8 世纪中叶, 中国古人在书中记载, 水是由阴气和阳气紧密结合, 故难以被分解[2]. 图1 选自牛顿Opticks一书, 牛顿在18 世纪初认为粒子与粒子由某种力结合, 该种力在粒子靠近时极强, 之后使各粒子稳定在一定的距离上[3].

图1 牛顿Opticks 中的关于化学键的表述Fig.1 Depiction of chemical bonds in Opticks by Newton

在18～19 世纪, 有多位化学家对化学键的表述方式提出过自己的观点. 如Higgins 等[4]在1789 年提出用分力理论来解释化学键的强弱; Frankland[5]和Couper[6]都认为化学键的性质会受两端原子性质的影响.

1861 年, Loschmidt[7]首次对不同化学键做了具体的定性定量描述(见图2), 他用不同大小的圆圈组合代表不同的原子, 详细解释了不同原子间形成单键、双键和三键的过程, 如小圆是氢原子, 大圆是碳原子, 氧原子和氮原子分别用2 个圆圈和3 个圆圈描述. 一些分子, 如图2 中的70 号和117 号, 可以明显分辨出是CH2CHCHO 和CH3CONH2. Boltzmann[8]在1898 年提出的理论中认为, 原子的外层有活性区域, 只有当活性区域接近或重合时, 才能产生化学键用以连接对应的原子.

图2 Loschmidt 用圆圈对化学键的描述Fig.2 Loschmidt indicated circles to demonstrate various chemical bonds

Lewis[9]在1916 年发表了The atom and the molecule, 他归纳了电子结构的想法后, 提出了立方体的原子分子价电子结构(见图3), 原子或分子中的价电子轨道为立方体, 电子占据立方体的各个顶点, 且当立方体的8 个顶点都有电子占据时, 其结构最为稳定. 分子通过原子的立方体结构结合, 并共享电子, 形成单键、双键等. 另外, 原子在分子中形成8 电子立方体结构后, 电子两两结合形成电子对, 并重新以四面体的形状排布. 之后, Langmuir[10-11]进一步提出原子的价层理论和八重电子理论; Lewis[12]更是提出了分子中的原子通过共享电子对形成化学键, 同时满足8 电子结构, 从而形成了Lewis 结构式理论.

图3 Lewis 的立方体原子电子结构Fig.3 Lewis’ cubic molecular electronic structures

在Lewis 结构式理论被提出之后, 利用量子力学原理的现代化学键理论开始逐步形成.Heitler 等[13]在1927 年提出的Heitler-London 波函数方程奠定了价键理论的基础. 由于电子不可区分且是费米子, 故在加入Heisenberg[14]的共振部分后, 描述氢分子基态的Heitler-London 波函数基本表述为ΨA和ΨB的双重简并的形式:

式中:ψ1,ψ2为电子1、2 在氢原子a 上的本征函数;φ1,φ2为电子1、2 在氢原子b 上的本征函数; 重叠积分由S=∫ψ1φ2ψ2φ1dτ表示.

图4 为2 个电子在ΨA部分分别沿原子核a, b 的键轴移动z1,z2时, 波函数的3 维与2 维投影图像. 可以看出, 波函数有2 个红色区域代表的波峰, 表明不同的电子占据不同的原子轨道; 而当2 个电子在原子中心靠近时, 2 个波形会产生重叠从而成键. 但是, Heitler-London波函数忽略了同极键的电离能[13,15], 从而导致成键能量被低估.

图4 在氢分子中沿键轴移动时的Heitler-London 波函数ΨA 部分等值面Fig.4 Iso-surface of H2’s electrons’ Heitler-London wavefunction ΨA

现代基于价键理论的方法已经可以描述分子基态与激发态、富电子键等不同化学体系[16-20]. 总的来说, 在价键理论中电子对原子轨道的占据相对独立, 2 个自旋不同的电子可以组成电子对, 原子间通过共享电子对形成化学键, 其中仅价层电子参与成键过程. 这样, 电子在价键理论中就以定域化的形式存在. 由于价键理论基于人类3 维认知且易于理解, 故相关研究人员倾向于用类似价键理论的电子存在方式来理解化学现象. 但是, 价键理论最初受到的挑战是因为无法正确描述基态氧气分子的顺磁性, 而其对于诸如苯环的共轭效应的描述也不甚准确.

分子轨道(molecular orbital, MO)理论比价键理论稍晚提出. 不同于价键理论, 分子轨道理论认为单个电子的贡献是对于整个分子, 即电子以离域化的方式存在[21]. Mulliken[22]在1928 年提出了分子中电子的量子数概念; Lennard-Jones[23]在1929 年写下的首个波函数, 被视为分子轨道理论的起源. 在分子轨道理论中, 分子被描述为由多个分子轨道组成的整体,一个分子轨道波函数φj可被多个原子轨道χi的线性组合所定义:φj=cijχi, 这里系数cij可经过变分法解相关的Schrödinger 方程=EΨ来得到, 其中为哈密顿算符,E为本征值. 分子轨道理论将氢分子的波函数Ψ写为

相比于Heitler-London 波函数,ψ1φ2+ψ2φ1部分是一致的,ψ1ψ2+φ1φ2为被忽略的电离项部分. 图5 为和Heitler-London 波函数类似的分子轨道理论氢分子波函数的等值面图.由于加入了电离项, 当一个电子在原子成键轴上移动时, 其在2 个原子位置都会产生波峰, 说明对于2 个原子都有贡献, 导致该电子无法被明确定位和分辨.

图5 在氢分子中沿键轴移动时的分子轨道波函数Ψ 等值面Fig.5 Iso-surface of H2’s electrons’ wavefunction Ψ in terms of molecular orbitals

Hartree[24-25]在1928 年提出了自洽场(self-consistent field, SCF)法, 认为多电子体系的哈密顿算符可以看成是单电子哈密顿算符的线性相加. 这样一来通过电子的空间坐标, 多电子体系的波函数就可以由单电子波函数的简单乘积求得. 但是, Hartree 的方法没有考虑Pauli不相容原则, 于是其学生Slater[26]和Fock[27]在1930 年将Slater 行列式加入SCF 法得到波函数的反对称形式, 得到了从头算的Hartree-Fock(HF)法. H¨uckel[28-29]从1930 年开始在分子轨道方面做了很多工作, 尤其是通过分子轨道理论成功解释了苯环的电子结构, 据此提出了日后成为判断芳香烃基准的H¨uckel 规则. 这些工作不仅体现出分子轨道理论的优势, 也使分子轨道理论成功地被化学界接受. 但是, HF 方法得到的单行列式波函数由于没有考虑电子相关性[30-31], 导致电离项的数值较大从而使键能被高估. 于是, 后来研究人员通过组态相关(configuration interaction, CI)方法[32], 即用各个组态的波函数线性组合成的波函数来描述无法用单行列式波函数描述的分子体系.

总之, 分子轨道理论和价键理论各有优势. 分子轨道理论的数学表示以微积分和线性代数为主, 使得通过计算机编程解Schrödinger 方程十分便捷高效, 由此化学体系需要的能量、光谱等性质都可以通过对应的波函数计算得出. 但是, 人类的直观认知是建立在3 维空间内的,高维波函数不仅难以想象, 而且离域化的电子也无法在化学反应内被标记. 而价键理论则通过电子对来描述化学体系, 符合人类的思维认知, 通过电子的流动解释化学反应, 易于被研究人员所接受.

图6 为基态水分子的电子结构, 图中价键理论与分子轨道理论给出了完全不同的描述. 图6(a) Lewis 结构式标示了成键和孤电子对; 图6(b)描绘了价键理论的电子结构猜想;图6(c)展示了计算得出的水分子基于价键理论的轨道, 其中成键和孤电子轨道可以明显地被分辨出来; 图6(d)解释了计算得出的水分子离域化分子轨道, 最高占据轨道(highest occupied molecular orbital, HOMO)与最低空轨道(lowest unoccupied unmolecular orbital, LUMO)由虚线分割. 由此可以看出, 价键理论可以比较明确地反映出氢氧单键和孤电子对的位置; 而分子轨道理论采用成键和反键轨道, 以及轨道间的杂化来反映化学键. 水分子的分子轨道采用Gaussian09W D.01[33], 在RHF/6-31G(d)[34]的计算水平下, 由Gaussview5[35]绘制得出.

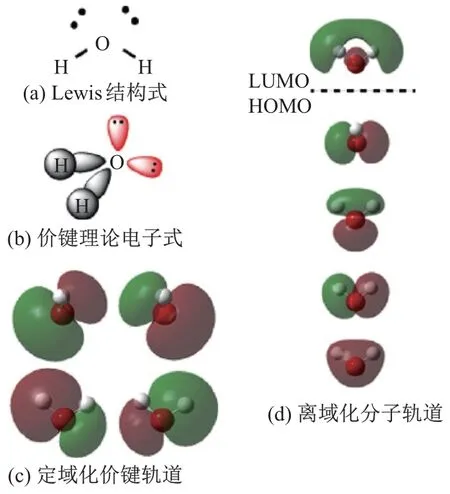
图6 基态水分子的电子结构Fig.6 Electronic structure of water molecule at its ground state

由此可见, 即使分子轨道理论和价键理论最终都可以收敛[36-37], 但其对于同一体系大相径庭的表述, 使得化学界关于孰优孰劣的讨论从未停止. 事实上, 研究人员一直在寻找如何在2 个理论间转换的办法,如Edmiston-Ruedenbery 法[38]、Foster-Boys 法[39],以及Pipek-Mezey法[40]等建立在分子轨道理论上的定域化方法, 但是这些方法所给出的定域化轨道不尽相同.另外, Hiberty 等[18]和Scemana 等[41]也曾将分子轨道拓展到价键理论, 但是他们的方法侧重于权重, 即从多个可能的电子结构中选取占比最大, 亦或出现频率最高的结构作为参考. 如何连接分子轨道理论和价键理论, 成为理论化学的热点问题之一. 而由于多电子波函数的高维空间无法被可视化, 使得波函数的边界界定问题成为一个难点.

根据前人经验, 本课题组结合HF 波函数、动态蒙特卡洛(dynamic Monte Carlo)模拟和拓扑(topolagy)结构等概念, 提出了dynamic Voronoi Metropolis sampling (DVMS)法, 可以在一定程度上简便地由HF 波函数推导到定域化的分子电子结构.

2 DVMS 方法介绍

2.1 波函数(wavefunction)

DVMS 法的分子构型由Gaussian09[33]在B3LYP/6-31G(d)[34]的理论水平下优化得来.波函数由Firefly[42]利用稳定的分子构型在HF/6-31G(d)[34]的理论水平下计算求得.

2.2 波函数单元(wavefunction tile)

一个波函数单元由单元内所有电子的空间坐标来定义.

在用反对称Slater 行列式描述的空间波函数Ψ中, 考虑同自旋的3 个电子的位置交换, 会对波函数产生如下影响:

在电子位置的交换过程中, 只有波函数的象限根据电子交换次数的奇偶性发生了改变, 而其他属性都不变. 因此, 如果仅考虑波函数的正值象限, 则对于体系内含有N个同自旋的电子,在固定另一组自旋电子的假设下, 其空间波函数具有0.5N!种可能的排列, 每一种排列被称为波函数单元, 用3N维向量r1表示.

波函数单元在多电子波函数中的意义, 最早被Glauser 等[43]研究. 结果显示, 对于锂和铍原子, 仅仅绘制一个波函数排列单元就可以得到包含核电子与价电子的电子结构. 然而, 当出现3 个同自旋电子时, 电子可以在不改变波函数正负值的情况下周期性地排列. 于是需要定义波函数排列单元之间的边界, 用以区分这些单元.

2.3 Voronoi 拓扑图形(Voronoi tessellation)

波函数单元的边界界定是采用拓扑结构Voronoi 图形来完成.

在Voronoi 分解中, 分布着不同位置的多个Voronoi 单元. 将一个随机子置入其中, 判断该随机子离哪个Voronoi 单元最近, 即将其归于该Voronoi 单元. 据此, 如果引入的随机子数量足够填满整个Voronoi 图形, 则每个Voronoi 单元的边界将由这些随机子的归属给出. 图7为经典的Voronoi 图形在2 维空间内的反映, 图中的黑点代表Voronoi 单元, 每个单元的区域由不同颜色的点根据边界判定条件分布得来.

图7 2 维空间的Voronoi 分解Fig.7 A Voronoi tessellation at two-dimensional space

在高维波函数单元内, Schmidt[44]提出用波函数的极大值点的波函数单元来定义Voronoi 单元位置, 通过随机3N维向量vm与间的距离来描绘波函数单元的边界.

Scemama 等[45]做的研究工作, 展示了水分子的波函数极大值单元, 是一种价层电子以氧原子为中心形成的接近正四面体的电子结构. 但是, 极大值的波函数单元并不总是正确的, 尤其对于分子来说, 如何寻找正确的波函数单元是面临的问题[46].

2.4 动态蒙特卡洛(dynamic Monto Carlo)

利用Metropolis[47]算法, 让波函数单元沿波函数正值区域自动扩散, 使其最后能收敛平衡. 以极大值的波函数单元的电子向量rlmax为起点, 在单一时间线t上通过正态分布, 产生随机子rt, 满足如下迭代条件:

式中:σ为正态分布标准差;μ为正态分布期望;ζ为0 到1 之间的随机数.

2.5 动态Voronoi Metropolis 取样

L¨uchow 等[48]在电子的自洽场中心方法中, 提出波函数单元可由随机电子的对应平均位置来定义. 据此, 通过与以上概念的结合形成了DVMS 算法的雏形.

首先, 对给定的收敛波函数Ψ, 输入对应体系所有电子的3 维随机坐标r, 计算波函数的极大值Ψmax, 输出对应电子组的坐标, 将其作为DVMS 法中波函数单元V0的初态坐标. 然后, 通过Voronoi 图形原理在该单元内产生n个平行独立随机子rnt, 下标t为时间单位; 采用Metropolis 算法使这些随机子能在判据条件下在单元内扩散, 同时波函数单元随着时间推移由同一时间内随机子的平均值动态更新. 最后, 当波函数单元对应的Ψ值稳定时, 波函数单元视为收敛, 并用该时的波函数单元中随机子在各个维度的平均位置代表分子的稳定电子结构.具体公式表述为

3 结果与讨论

3.1 原子

图8 展示了通过计算相应原子波函数的极大值的电子空间坐标, 得到的非金属原子诸如碳、氮、氖原子的电子排布. 较大的球形代表原子核, 较小的黄色球形代表α电子, 绿色球形代表β电子. 内层电子位于原子核中心, 价层电子与原子核距离相对较远.

图8 碳、氮、氖原子的电子在波函数极大值时的空间坐标Fig.8 Electrons’ positions at their maximum wavefunction value of carbon, nitrogen and neon atom

从图中可见, 各个原子中都含有2 个内层电子, 这2 个电子位于原子核位置, 而价层电子的排布较为特别. 碳原子的4 个价层电子按照自旋的不同分为3 个α电子和1 个β电子;3 个α电子呈类似等边三角形排列在一个平面内,β电子和内层电子的连线, 与α电子所在平面垂直, 这些电子到原子核距离相同. 氮原子比碳原子多1 个α电子, 4 个α电子围绕原子核呈正四面体结构. 氖原子的4 个α与4 个β电子分别组成2 个正四面体, 围绕原子核组成一个立方体, 暗示了8 电子稳定结构的构型应由2 个四面体组成. 虽然这样的电子排布不符合Mulliken[22]的原子轨道概念, 但在很大程度上还原了图3 中Lewis 的八角结构[9], 说明分子轨道理论与价键理论有着潜在的共通性. 波函数极大值的电子空间位置可以较好地描述原子, 但对于分子来说, 极大值已经不足以正确描述其电子结构, 因此需要引入DVMS 方法.

3.2 单行列式波函数

氮气(N2)的波函数极大值的电子结构显示的是单键[46], 与认知上的氮氮三键不符. 分子轨道理论认为, 氮氮三键由2 个Π 轨道和1 个Σ 轨道组成, 通过DVMS 算法氮氮三键的电子对结构被分析出来. 图9 展示了氮气分子DVMS 计算过程, 图片选自文献[46], 图中k代表时间步数, 蓝色球形代表原子核, 黄色球形代表α电子. 由于没有加入电子相关性,α和β电子的位置理论上可重叠, 故仅显示各个α电子的平均值位置. 随着时间k的增大, 在DVMS 迭代过程中, 电子位置由极大值的单键逐渐过渡到氮氮三键, 并稳定在此位置. 在氮气的平衡电子结构上, 各个电子的平均值位置显示, 2 对孤电子对分别位于2 个原子核的外侧, 原子核中间由3 对成键电子对组成三键电子结构. 因此, 氮气的分子轨道波函数可以还原出符合认知的电子结构.

图9 氮气分子的DVMS 计算过程Fig.9 DVMS computational process of dinitrogen molecule

水(H2O)、乙烯(CH2CH2)、氟气(F2)等分子的电子结构也可以通过对应的波函数成功还原出来[46,49]. 图10 展示了乙烯、水、甲醛(CH2O)和氟气分子的DVMS 平衡态下的电子结构,波函数由一个行列式描述, 依然仅显示所有的α电子, 以之来代表电子对位置. 较大的球代表原子核, 其中氢原子为灰色, 碳原子为黑色, 氧原子为红色, 氟原子为绿色; 较小的黄色球代表α电子. 内层电子位于原子核中心, 价层电子与原子核距离相对较远. 由图可知, 乙烯的碳碳双键结构由2 个电子对与原子形成的弯曲键表示; 水分子中的氧原子孤对电子对和单键电子对与价键理论的结构相似; 甲醛的碳氧双键在形式上与乙烯相近, 但更靠近氧原子, 表明氧原子具有更强的电负性; 氟气分子由单键以及原子侧的各3 对孤电子对描述, 符合经验认知.

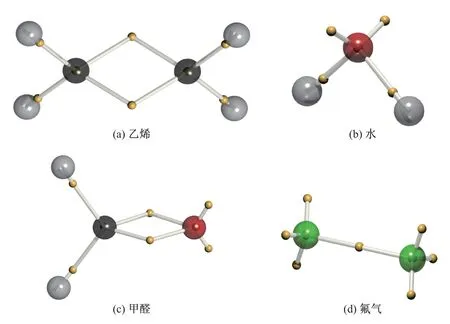
图10 乙烯、水、甲醛和氟气的DVMS 电子结构Fig.10 DVMS electronic structures of ethylene, water, formaldehyde and difluorine

Linnett[50-51]提出的双四重理论暗示氧(O2)分子的基态不应严格以电子对的方式来描述,从而可以在价键理论层面上解释氧分子的基态三重态电子结构(见图11). 通过氧分子三重态的限制性开壳层HF 波函数, DVMS 法从分子轨道理论中解析出了和Linnett 设想一致的结构. 图11 中, 较大的球代表原子核, 其中氧原子为红色, 氮原子为蓝色; 较小的黄色球形代表α电子, 绿色球代表β电子, 而图11(a)为Linnett 描述的三重基态氢气的双四重电子结构. 实际上, 由于采用限制性开壳层波函数描述三重态氧分子, 故氧分子的9 个α电子可认为是遵循氟气分子的波函数轨道性质, 而7 个β电子则遵循氮气分子的波函数轨道性质. 因此, 氧分子的电子结构可以理解为分别由氟气和氮气分子的DVMS 电子结构的线性组合形成. 一氧化氮(NO)的结构也可以解释为单重态氧气分子的双键结构和氮气分子的三键结构的DVMS 电子结构的线性组合, 故DVMS 的一氧化氮结构也没有展示电子对, 但是每个原子都保持了8电子稳定结构.

图11 三重基态氧气与一氧化氮的DVMS 电子结构和Linnett 结构Fig.11 Electronic structures of triplet dioxygen and nitrogen oxide by DVMS and Linnett

3.3 电子的组态相关性

双碳(C2)分子电子结构的描述在化学界是一个争议已久的话题, 有一种观点认为双碳分子含有四键结构[52-53], 但是四键结构应该如何存在？

图12(a)展示了双碳分子的波函数导出的DVMS 电子结构的一种四键结构, 碳原子核以黑色大球表示, 不同自旋的电子以不同颜色小球表示[46,52]. 如果考虑双碳分子中的价层电子对2 个碳原子的贡献是相同的, 那么该四键结构是合理的. 但是, 振动频率分析暗示双碳分子的结构接近于双键, 于是双碳分子的Lewis 结构式经常被写为:C==C:, 那么孤电子对与成键电子对针对2 个碳原子的贡献明显不同. Shaik 等[52]将双碳分子的电子结构描述为含有碳碳三键的单重态双自由基结构, 其中在每个碳原子侧的1 个自旋不同的孤电子通过耦合形成第4根化学键(见图12(b)). 实际上, 单行列式波函数已经不足以准确描述双碳分子的电子态, 众多研究表明, 双碳分子的电子态需要采用引入电子相关性的组态相关的线性组合波函数方法来进行描述[54-55]. 由于DVMS 法本身不改变波函数, 故DVMS 法的一个优势就是适用于不同形式的波函数上. 对双碳分子的组态相关计算中发现, 除了基态组态外, 另外一个电子从Σ 反键轨道跃迁到Σ 成键轨道的组态也占有较高比重, 正确的波函数应由这2 个组态线性组合而成. 图12(c)展示了在通过将对应的多组态波函数进行DVMS 计算后, 双碳分子的平衡态电子结构. 从其结构可以看出, 双碳分子的碳碳键近似于三键, 而二端各有1 个孤电子, 为单重态双自由基结构. DVMS 计算结果在一定程度上论证了Shaik 的猜想, 证明了用电子相关性描述双碳分子的必要性和合理性. 此外, DVMS 法也适用于其他非碳分子的电子相关性计算, 如氧化亚镁(Mg2O). 图13 显示了氧化亚镁DVMS 结构的单重态双自由基结构, 图中的中心氧原子(红色大球)为8 电子稳定结构, 2 个镁原子(黄色大球)外侧各有1 个自旋相反的孤电子.

图12 双碳分子的DVMS 研究Fig.12 DVMS research upon dicarbon

图13 氧化亚镁分子的DVMS 研究Fig.13 DVMS research upon Mg2O

3.4 共轭分子

单环芳香烃分子在生物医药、石油工业、太空探索等方面都有较大的应用价值[56-57], 这使得该类分子的研究具有重大的科学意义, 其中苯环作为最基本的芳香烃化合物之一, 对其电子结构的讨论也一直持续至今.

1825 年, Faraday[58]首次报道了苯环分子; 之后, Kekul´e[59-60]提出的单键与双键交替的结构, 一直到现在都是苯环结构的主要描述之一, 但是Kekul´e 的结构式无法解释一些实验现象. H¨uckel[29]利用离域分子轨道将苯环的化学键描述为覆盖在6 个碳原子上的化学键, 从而得到了能较符合实验现象的共轭结构. 在苯环的共轭结构中, 所有碳碳键一共包含18 个电子, 由6 个碳原子共享, 这用Lewis 结构式难以描述. 那么, 定域化的电子能否描述苯环的Π 键电子结构呢？

本课题组利用DVMS 法分别对苯分子的基态单行列式波函数和组态相关的线性组合波函数, 进行了电子结构的计算[61], 结果如图14 所示. 图中, 黄绿色小球代表α、β的电子, 黑、灰色小球分别代表碳原子和氢原子. 在不引入电子相关性的前提下, DVMS 法会收敛到类似于Kekul´e 结构式的由电子对组成单双键交替的电子结构(见图14(a)). 在引入电子相关性, 仅考虑电子从Π 成键轨道到Π 反键轨道的跃迁, 随着加入的组态数增加到21 个, DVMS 法收敛到了一个不同于Kekul´e 结构式的电子结构. 在该电子结构中, 化学键以单电子组合而非电子对组合呈现; 每组碳碳键都由3 个电子组成, 并由组合(2α+β)与(α+2β)交替排布. 采用这种方式后, 18 个电子被平均分布在6 个碳碳键中, 从而在价键理论层面解释了共轭π 键. 事实上,无论是Kekul´e 还是共轭的电子结构式, 都可以转换为1 个与原结构镜面对称的结构, 因此苯分子也是一个共振分子. 波函数组态数目的增加导致收敛的共振电子结构改变, 在文献[59]中有着详细的说明.

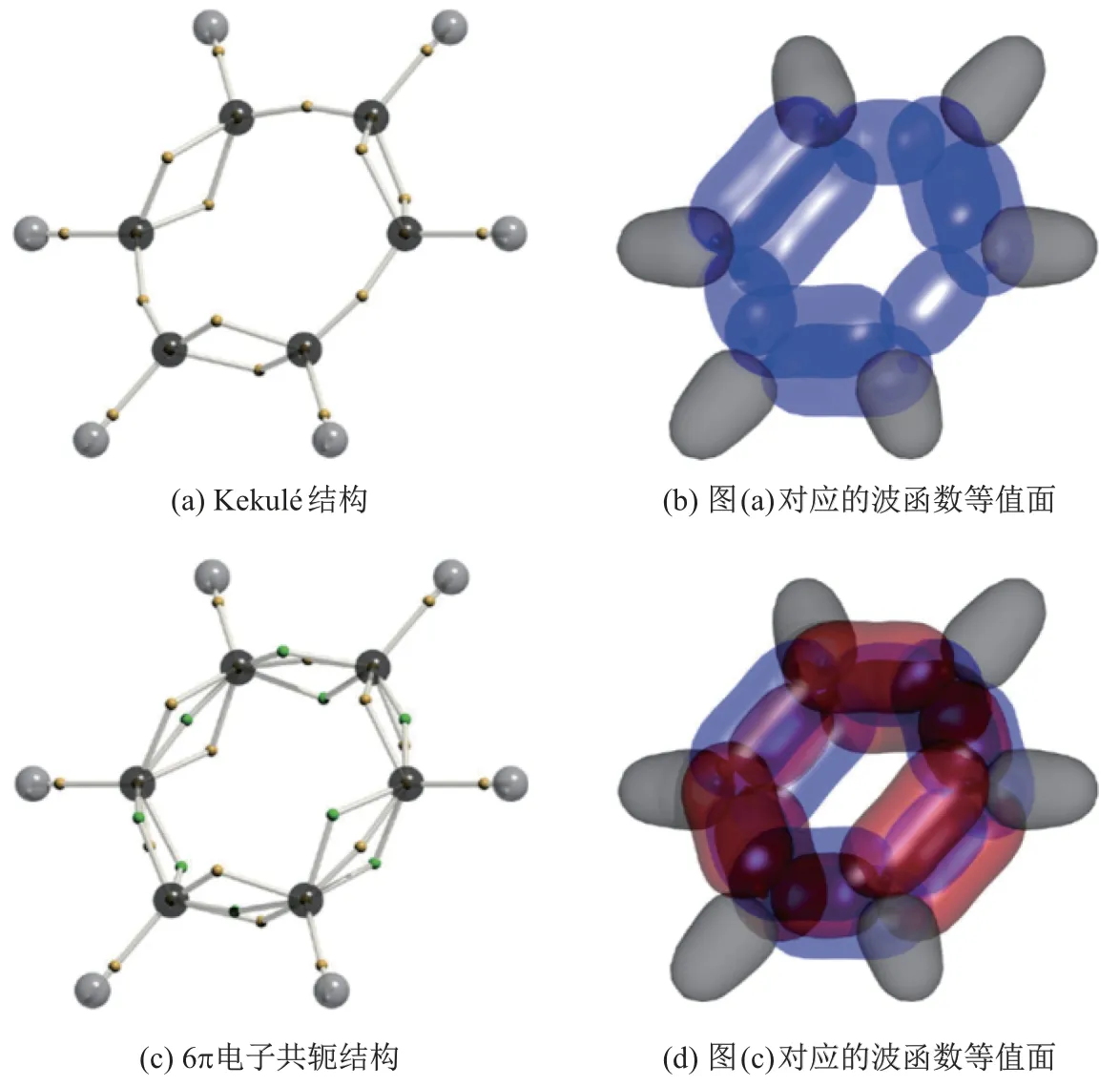
图14 苯环的DVMS 电子结构Fig.14 DVMS electronic structure of benzene

3.5 化学反应

在实际应用中, Kermack 等[62]、O’Hagan 等[63]、Budzikiewicz 等[64]、邢其毅等[65]提出的化学反应箭头描述法一直被运用至今. 通过将轨道定域化, 内禀成键轨道法与电子定域法已经能够成功计算出某些特定化学反应机理的电子流向[66-67]. 然而, 箭头描述法依靠的基础是通过电子对的形式展现的Lewis 电子结构式, 而且很多分子及其跃迁结构都不能被单行列式波函数或定域化轨道法正确地描述. 但是, DVMS 法已经被证明可用于各种不同形式的波函数.

由丁二烯与乙烯反应生成环己烯的反应即是著名的Diels-Alder[4+2] 反应(DA 反应).高等学校教材中通常用箭头表示的3 对电子对的转移来描述该反应的化学机理[65,68](见图14(a)), 而分子轨道理论强调分子轨道从反应物平缓过渡到生成物. 图15 展示了DVMS 从分子轨道理论中模拟出的DA 反应的可视化描述[69]. 图15(a)和(b)为通过弧线箭头对该反应的描述; 图15(c)为势能面上数字所对应各片段的DVMS 电子结构, 以波函数等值面的形式展示.图15(c)中, 灰色气泡代表碳氢化学键; 绿色气泡代表反应中没有变化的碳碳键; 红色与紫色气泡代表反应中移动的电子.

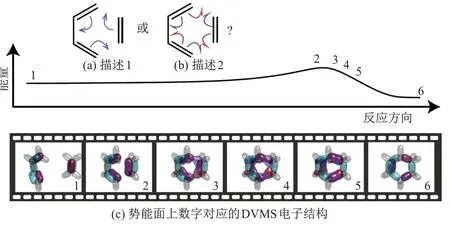
图15 Diels-Alder[4+2]反应的化学路径势能面和DVMS 电子态描述Fig.15 Depiction of transitions in terms of electronic states during Diels-Alder[4+2] reaction by DVMS

本课题组从DA 反应路径的势能面上选取了一些片段的分子构型, 包括反应物、过渡态和生成物, 之后通过DVMS 法计算每个构型的电子结构, 最后将每个构型的DVMS 结构串联起来, 组成一个完整的DA 反应电子转移路径. 片段2～5 主要描述了反应的关键过程, 即从旧键的断裂到新键的生成. 在等值面描述中, 绿色半透明区域的电子对保持化学键状态, 红色半透明区域反映了化学键的断裂与生成. 片段3 的对应等值面显示, 参与反应的化学键从电子层面断开,α(红色半透明区域)与β电子(紫色半透明区域)分别向相反方向移动, 与另外的β和α电子组成新的成键电子对. 同时, 反应物的双键中未参与新成键的电子(绿色半透明区域)让位或补位形成对应的双键或单键. 其反应方式可以用鱼钩箭头[65]表述成图15(b)中所示: 参与反应的化学键电子对先拆分, 再组合. DVMS 法给出的电子转移方式, 与通过自旋耦合价键理论描述的均裂机理十分相似[70]. 但是, DVMS 法仅通过分子轨道理论的化学反应路径计算结果,配合组态相关的对应波函数, 就模拟出了此反应过程, 说明DVMS 法在计算化学反应方面也有潜在的能力. 文献[69]对DVMS 法在化学反应方面的工作, 有着更为详细的介绍.

4 结束语

本课题组自主开发了具有创新性的化学键分析算法——DVMS 法, 并详细介绍了DVMS法现阶段版本的一些成功应用. DVMS 法的目的是定义和探索多电子波函数单元, 描述化学键结构, 从而建立分子轨道理论与价键理论的连接, 打破理论与实验的认知壁垒. DVMS 法证明了波函数单元可以推导出电子定域化的Lewis 和Linnett 结构式, 其形式符合实验化学认知. 通过探索波函数单元, 解释了双碳分子的双自由基结构, 同时首次解释了苯分子的共轭π键中稳定的电子排布形式. 另外, DVMS 法也能从电子层面模拟化学反应的反应机理. 由于DVMS 法本身不改变波函数的任何性质, 故理论上可以广泛地适用于任何波函数形式, 不管是单行列式的, 还是多组态相关的. 综上所述, 作为一款探索电子结构的有效工具, DVMS 法的应用前景十分广阔.

致谢感谢DVMS 法的联合发明者、新南威尔士大学的Timothy Schmidt 教授与Terry Frankcombe 副教授对该研究的指导; 感谢澳大利亚DATA61 的Phillip Kilby 博士提供的搜索算法; 感谢上海大学Jeffrey Reimers 教授对此研究的支持.