不平衡数据中基于异类k距离的边界混合采样
2021-02-25于艳丽江开忠盛静文
于艳丽 江开忠 盛静文
(上海工程技术大学数理与统计学院 上海 201620)
0 引 言
不平衡数据指的是数据集中存在不同类别样本的数目相差很大。以二分类数据为例,征信领域中诚信与违约、医疗领域中健康与绝症、邮箱里正常邮件与垃圾邮件,这些二分类数据中某一类数据数量远多于另一类,这样的数据就称为不平衡数据[1-4]。将数量较少的类别称为少数类,将数量较多的称为多数类。现实世界中,随处都有不平衡数据,且错分两类数据的代价是不同的,通常对少数类的正确判断更有意义[5]。传统的分类方法对于平衡的样本数据已经表现出很好的性能,但是对于不平衡数据,分类器的性能在下降。如何提升传统分类方法对少数类的识别准确率成为机器学习中一个急需解决的问题[1,6]。目前,解决不平衡数据问题的方法可以分为如下两类:
1) 改进分类算法以提高对少数类样本的识别,如:代价敏感学习[7]、集成学习[8]和单类学习等。AdaBoost算法[9]就是其中比较经典的处理不平衡数据的集成算法,本身就具有代价敏感的特性,能够给予误判样本更高的权重。一些算法通过更改AdaBoost算法中样本更新权重来增加正确率,如AdaCost算法[10]和RareBoost算法[11]。还有些算法将采样算法与集成算法相结合,例如NIBoost[12]、RSBoost[13]和PCBoost[14]。另外还有其他分类算法,如:SVM[2]、决策树、神经网络等,它们也经常被用来处理不平衡数据。
2) 通过处理原始数据来提高对少数类样本的识别,即对数据进行欠采样或者过采样来达到数据平衡的目的。欠采样是剔除多数类样本数量,过采样是增加少数类样本数量。欠采样算法有基于密度的欠采样[1]、基于权重的欠采样[15]等,其很容易造成有用信息的减少。过采样算法中的SMOTE[16]算法是主流算法,其通过线性插值的方法增加少数类虚拟个体,使得分类结果得到改善,但具有如下缺点:① 参与合成的少数类可能是噪声样本,进而影响新样本质量;② 没有根据少数类样本的重要性,进行区别化选择;③ 生成新样本时,正负类样本混杂,从而导致边界模糊问题;④ 合成样本仅在2个点的连线上产生,分类器易过拟合等[17]。针对SMOTE算法存在的问题,学者提出了很多改进的SMOTE算法。董燕杰[18]研究了Random-SMOTE方法,把直线插点改成三角形内插点;袁铭[19]提出了R-SMOTE算法,在n维球体进行插点。这些方法对减少过拟合现象均有一定作用,但都是对全体少数类样本进行过采样,准确率提升有限。候贝贝等[20]用np-SMOTE方法在边界少数类周围合成少数类,使其从非安全样本变成安全样本,突破了原有的少数类样本点的范围,但易产生噪声。Han等[21]用Borderline-SMOTE算法定义了边界,解决了没有区分少数类点重要性的问题,但对于边界的定义仅依靠异类点的数量,不够细致。古平等[5]提出了SD-ISMOTE算法,采用了不同的过采样算法,能够解决过拟合的问题,但是目标依旧是全体少数类样本。Batista等[22]提出了SMOTE与Tome Link结合的算法,Last等[23]提出了一种基于k-means聚类的SMOTE过采样方法,两者都有效地解决了噪声问题。上述过采样方法的改进在处理不平衡数据上都有一定优势,但大部分没有对参与新样本合成的少数类样本进行区别化对待,或者区分度不高,从而导致少数类的识别率不够高。
本文提出一种不平衡数据中基于异类k距离的边界混合采样算法,主要目标是区分边界样本与非边界样本,对参与合成的边界少数类样本做精细区分,以便增加产生新样本的质量,提高少数类样本的分类正确性。首先,生成边界集,只对其中的少数类样本进行过采样,从而对少数类样本点进行区别选择;其次,根据支持度对边界集中的少数类样本进行细分,能够更加细致严谨地给每一个少数类样本定位,少数类样本虚拟个体的产生根据类别的不同分别采用SMOTE、R-SMOTE、Random-SMOTE的过采样方法,改善过拟合现象;最后,对非边界集多数类样本基于异类k距离进行剔除,保留有意义的样本。
1 相关知识
1.1 分类问题
1.1.1二分类理论
假设在一个两分类问题中,数据集C=C0∪C1,C0∩C1=∅,其中C0为多数类样本,C1为少数类样本。标准化后的样本观测矩阵为:
当xi∈C1时,yi=1,称个体xi为阳性个体;即少数类个体;否则,yi=0,称个体xt为阴性个体,即多数类个体。
分类器超平面表示为:
w1x1+w2x2+…+wpxp=wTx=c
(1)
通常,超平面的系数和常数的估计可表示为下面优化问题的解:
(2)
即分类器的超平面法向量和常数是使得F1取最大值时的(w1,w2,…,wp,c),F1指分类评价指标中的F1分类(F-Score)。
1.1.2分类评价指标
通常来说混淆矩阵是评价一个算法分类效果的不二选择,混淆矩阵如表1所示。

表1 混淆矩阵
将实际为正类的样本分为预测为正类和预测为负类两部分,将实际为负类的样本分为预测为负类和预测为正类两部分,它们的个数分别简记为:TP、FN、TN和FP,则分类器的性能表示如下:
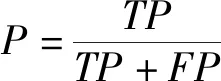
1.1.3最小距离分类法
已知类C及其中心μ,个体x到类C的距离定义为:
d(x,C)=d(x,μ)=(x-μ)T(x-μ)
最小距离判别准则为:已知两类C0和C1,对任意x,若d(x,C0) 1.2.1SMOTE算法[16] SMOTE算法流程如下: 1) 对于少数类样本中每一个个体x,以欧氏距离为标准计算它到少数类样本集C1中所有样本的距离,对所有距离排序,距离其最近的k个样本便是其k近邻。 2) 根据样本不平衡比例设置一个采样比例以确定采样倍率N,对于每一个少数类样本x,从其k近邻中随机选择样本yi。 3) 对于每一个随机选出的近邻yi,分别与原样本按下式构建新的样本: xnew,i=x+rand(0,1)×|x-yi| (3) 1.2.2R-SOMTE算法[19] R-SMOTE算法在n维球体内插值,算法流程如下: 1) 根据数据集不平衡比例设置一个采样倍率N,从少数类样本C1中循环选择样本x。 2) 从x的k个同类最近邻中随机选择样本y,构建新样本。 zi,j=xj-|yj-xj| (4) z2,j=xj+|yj-xj| (5) xnew,j=xj+rand(0,1)×|z2,j-z1,j| (6) 式中:xj代表样本x的第j个属性。 3) 如果D(x,xnew)>D(x,y),则废弃xnew,重新生成xnew。 4)xnew加入C1,当C1的样本数等于或相当于C0的样本时,结束过采样。 1.2.3Randmon-SOMTE算法[18] Random-SMOTE算法在三角形内生成新的样本点,算法流程如下: 1) 根据数据集不平衡比例设置一个采样倍率N,从少数类样本C1中循环选择个体x。 2) 在x的k近邻中随机寻找两个同类个体a、b,在两点连线上随机确定一点y,最后在个体x与y之间合成新的样本点xnew: xnew=x+rand(0,1)×(x-y) (7) BHSK算法作为混合采样算法,综合过采样与欠采样算法于一体。主要思路是凸显不同位置样本不同的采样重要性,所以采样方法要因样本位置而异,这样能产生有助于提高分类精确度的新样本,而如何区分样本的重要性是本文算法的重点之一。对于过采样部分,BHSK算法采用两种方法实现了对少数类样本递进式区分,分别是基于异类k距离边界集的识别、支持度的判定,从而筛选出不同层次的少数类边界点。对于欠采样部分,BHSK算法主要是通过异类k距离判别,从而删除远离边界的多数类点。 另一个相关问题是如何寻找适合各种不同位置少数类样本的采样方法与采样倍率。根据不同位置样本的不同特点,本文算法采用了三种过采样算法和倍率,有针对性地对不同样本进行过采样,产生更有意义的位于边界的新样本。 从数据层面对数据集进行分类,为了使类之间的样本数量均衡,实现较好的分类效果,基于支持向量机(SVM)的分类思想,超平面只与支持向量有关,而支持向量大都位于多数类样本和少数类样本的边界,所以在处理不平衡数据时边界集的识别是极其重要的[20]。BHSK算法的边界集是基于异类k距离来定义的,本文通过改进文献[24]中的k距离,提出一种异类k距离。 换言之,x的异类k距离是所有与x异类的点中,由近到远第k个异类点到x的距离。异类k距离可以评价一个样本点附近异类点的密度,异类k距离越大,说明附近异类点密度越小,反之则越大。 (8) (9) 定义4边界噪声点。若x=A0或A1,且其k近邻全是异类点,可以理解为深入异类点内部,则x为边界噪声点;由边界噪声点产生的新样本,可能存在质量较差的问题,所以以下B0和B1表示已经删除了噪声点的边界0类点与边界1类点。 定义5支持度。设x∈B1,m(x)表示x的最近k个近邻中属于B1的个体数,则m(x)为x的支持度。 根据支持度将B1分为三类,具体情况如下: (10) 在区分边界集的基础上再对边界集进行细分,目的是为了更加细致地对每一个少数类样本进行重要性评估,从而选择出每一个类别少数类样本适合的采样方法。 对于边界集少数类样本B1进行过采样。对于过采样方法,BHSK算法根据每个点对分类做出的贡献不同对三类边界点采用不同的过采样方法和过采样倍率,按照近边界则优的原则进行如下采样。总采样数量是D=C0-C1,按照3∶2∶1的比例确定三个类别中新生成样本的数量。 本文提出的BHSK算法具体如下: 输入:训练数据集C,近邻参数k,插值数量D。 输出:均衡数据集T。 2) 将B1根据支持度细分为B11、B12和B13。 5) 将train 1和train 2合并为train。 本文从UCI数据库选取8个数据集Abalone、biodeg、Ecoli、Shuttle、pima、glass、yeast、spambase,其中有些数据集是二分类数据集,比如biodeg、spambase、pima;有些是多分类数据集,比如Abalone、Ecoli、shuttle、glass、yeast。将abalone中”F”定义为少数类,其余为多数类;Ecoli数据中的标签为“pp,om”的样本定义为少数类,其他为多数类;将shuttle数据集中标签为“1”定义为多数类,其他为少数类;将glass标签中“2”定义为少数类,其他为多数类;将yeast数据集标签中“MIT”定义为少数类其他为多数类。数据集信息如表2所示。 表2 数据集信息 表3 不同算法在8个数据集上Recall对比结果 表4 不同算法在8个数据集上的F1-score对比结果 (a) Abalone (b) biodeg (c) ecoli 从表3可以看出,BHSK算法在少数类的识别上是比较有优势的,大部分数据集在本文算法的处理后得到的Recall值都高于文中列举的其他对比算法。因为本文在处理数据时,对少数类的边界点做了相应处理,较好地降低了由边界点分错而带来的不良影响,同时对非边界的多数类基于异类k距离进行删除,较好地保留了对分类有价值的样本点。虽然在Yeast、Spambase数据集上没有取得最优值,但相差不大,说明BHSK算法能够在一定程度上提高少数类的分类性能。 从表4可见,针对Yeast数据集,R-SMOTE算法的结果优于本文,由于该数据集的不平衡比率较大,且边界点重叠度较大,本文边界集阈值的设定可能对该数据集的分类性能产生影响,使得球体插值更适合于这个数据集。但是从整体来看,BHSK算法经过一系列处理以后,能够使少数类的准确性提高。 为了更加可视化本文算法与其他算法的比较情况,图1列举了本文算法与所有对比算法在不同数据集不同指标的得分情况,横坐标都表示打分的指标Precision、Recall、F1-score和Accuracy。纵坐标是分类结果打分情况,其范围在0~1之间。综上所述,BHSK算法优于SMOTE、R-SMOTE、Borderline-SMOTE和KOCDE算法,它可以更合理且有效地改善不均衡数据集中样本分布的不均衡程度,从而提高分类器的性能。 本文针对非平衡数据分类问题,提出一种基于异类k距离边界混合采样分类算法。一方面能够通过两次判别:边界判别与支持度判别,更加具体区分少数类样本重要性,并对细分的不同类别少数类采取不同的分类方法和不同的采样倍率,给距离边界越近的少数类越高重视;另一方面对非边界集的多数类点根据异类k距离阈值,删除远离边界的一部分点,从而构造平衡数据。实验结果表明,本文算法在一定程度上提高了数据集的分类性能,可将其应用于一系列评估和检测问题。但本文算法也存在一些不足,如边界集阈值与多数类非边界集阈值的选取方面理论依据不足,未来将在阈值方面进行研究。1.2 相关过采样算法
2 边界混合采样的BHSK算法
2.1 算法思想
2.2 基于异类k距离的边界集识别
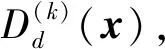

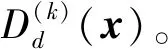
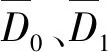
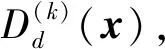
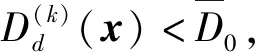
2.3 少数类边界样本集的细分
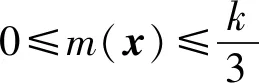
2.4 边界集的过采样方法与数量
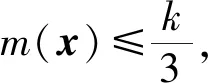
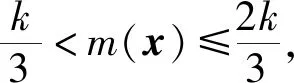

2.5 非边界集的欠采样
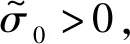
2.6 算法步骤
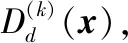
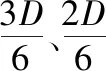
3 实 验
3.1 数据集的选择与分析
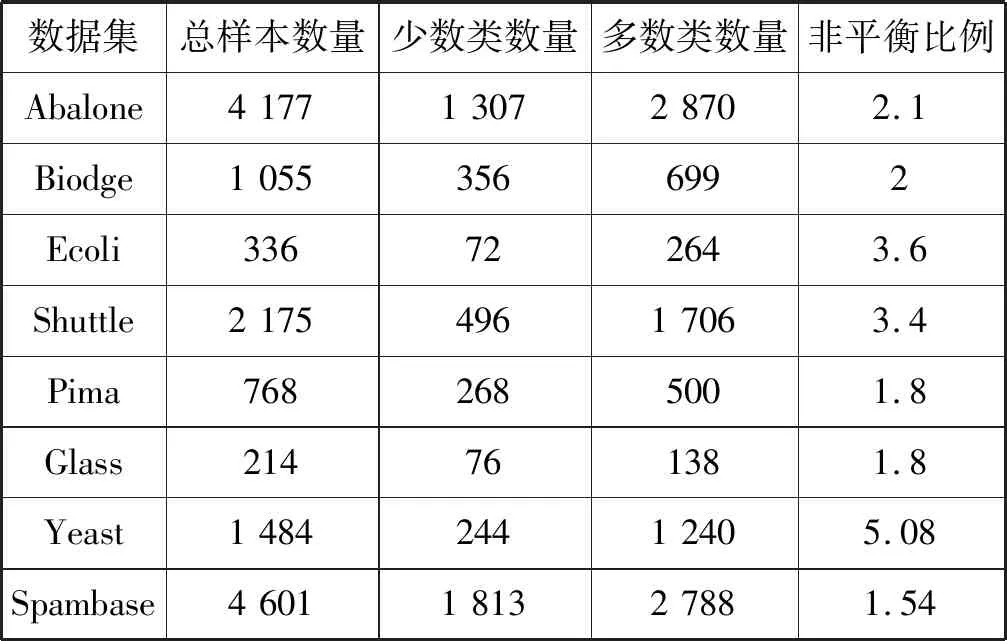
3.2 实验结果分析
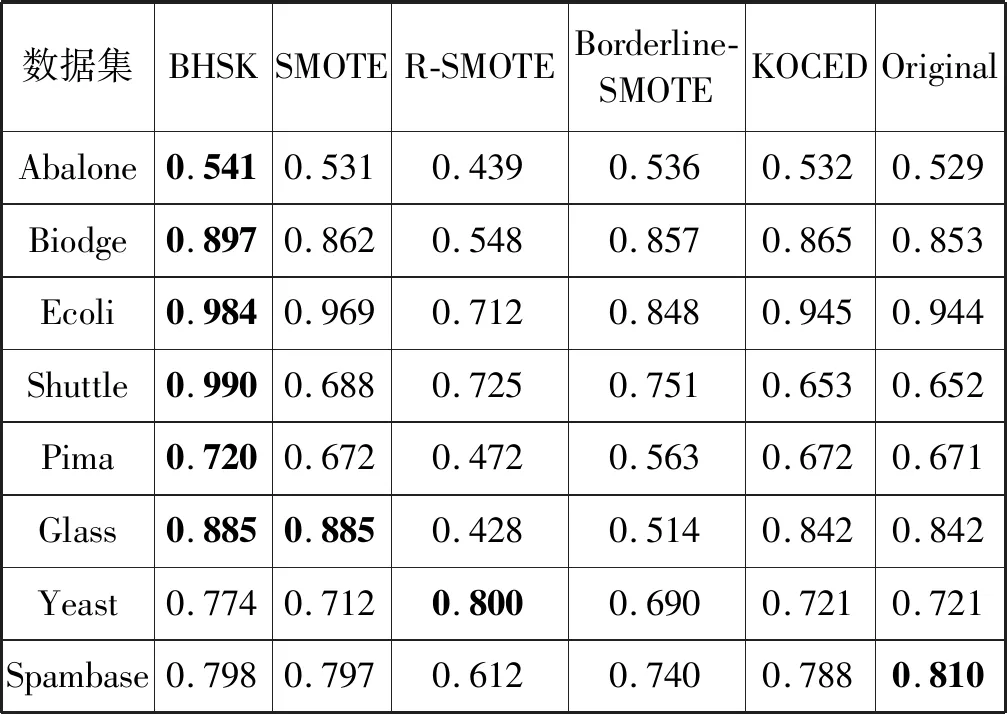
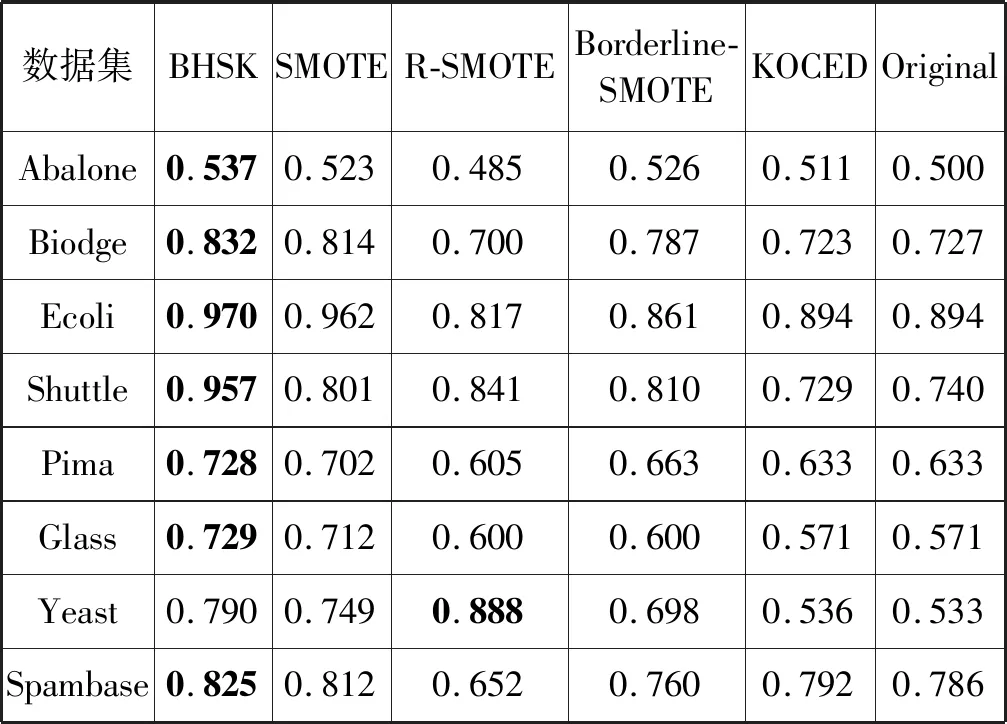

4 结 语
