大断面隧道机械化施工支护结构设计方法——以郑万高铁湖北段隧道为例

童建军, 刘大刚, 张 霄, *, 王志龙, 赵思光, 李佳旺

(1. 西南交通大学 交通隧道工程教育部重点实验室， 四川 成都 610031； 2. 西南交通大学土木工程学院， 四川 成都 610031)

0 引言

21世纪以来，随着经济的快速发展及综合国力的日益提高，我国隧道建造技术发展迅猛。当前，我国已经成为世界上隧道工程建设规模最大、建设速度最快、地质条件最复杂的国家。至2019年底，中国运营铁路隧道总长达18 041 km，在建铁路隧道总长约6 419 km，规划铁路隧道长约16 326 km[1]。然而，目前我国隧道施工的机械化程度较低，主要采用人工分部法施工，其开挖次数多、施工效率低、劳动力需求量大、劳动强度高，且难以适应高海拔、高地温、高寒、缺氧等极端环境。

为推动我国隧道施工技术的发展，提高隧道施工机械化，2017年5月，中国国家铁路集团有限公司批准了《郑万高铁大断面隧道安全快速标准化建设关键技术研究》科研立项，对大断面隧道机械化施工系列装备、隧道支护设计方法、大断面隧道施工工法及工艺等关键技术开展系统、深入的研究，目前已在18座隧道(47个工区)实现了机械化全断面法施工[2-7]。大断面隧道机械化施工主要采用全断面法[5]，该工法与传统分部法相比，在掌子面围岩及洞身围岩稳定性2方面存在较大的差异： 1)隧道掌子面围岩稳定性。全断面法与分部法相比[2]，掌子面面积大，导致掌子面挤出变形大、围岩稳定性差，合理的超前支护措施是控制掌子面稳定性的有效手段，因此，需研究适应于软弱围岩隧道全断面法的超前支护设计方法。目前，国内外学者针对隧道掌子面稳定性分析及超前支护设计方法开展了大量的研究工作，提出了多种掌子面稳定性分析模型[8-9]，建立了超前管棚力学分析方法[10]，并开展了注浆加固体强度参数方面的研究[11]。然而，目前的计算模型主要针对单一的超前支护措施，且尚无综合考虑多种加固措施的掌子面稳定性分析方法。2)隧道洞身围岩稳定性。与分部法相比，全断面法具有一次成型、及时支护、封闭快速等优势，减少了洞身段围岩扰动范围，隧道变形小，围岩稳定性高，支护结构所受围岩压力小[4-6]。因此，全断面机械化施工时隧道支护结构所受的荷载不是塌方荷载，需要研究形变压力计算方法。国内外学者采用理论推导、数值模拟、现场实测等手段，提出了多种形变压力计算方法[12-15]。其中，基于现场实测结果建立的半经验形变压力(围岩压力)计算方法在工程实践中应用最为广泛。然而，国外常用的隧道形变压力计算公式(Q法[12]和RMR法[13])都是基于当地的实测样本通过数理统计方法提出的，与各国施工工法工艺、管理水平等密切相关，具有区域性和局限性。因此，国外的隧道形变压力计算公式并不能直接应用到我国，必须广泛收集实测样本，统计出适用于我国隧道工程的形变压力计算公式。

为此，本文研究了隧道掌子面围岩稳定性分析方法及形变压力计算方法，并提出掌子面超前支护及洞身支护结构设计方法，以期为大断面隧道机械化施工支护体系设计提供理论支撑。

1 掌子面围岩稳定性分析方法

相关研究表明，砂质、土质围岩掌子面前方破坏面为直线或对数螺旋形[16-17]。由于目前缺少碎石土、块石等围岩掌子面破坏模式方面的研究，因此，将砂质、土质围岩掌子面破坏模式应用于其他软弱围岩(纯黏性土不在本文的研究范围)。基于经典棱柱-楔形体模型[18]，提出考虑3种超前支护措施(超前管棚、掌子面锚杆和掌子面预注浆)的三维掌子面稳定性分析模型，如图1所示。

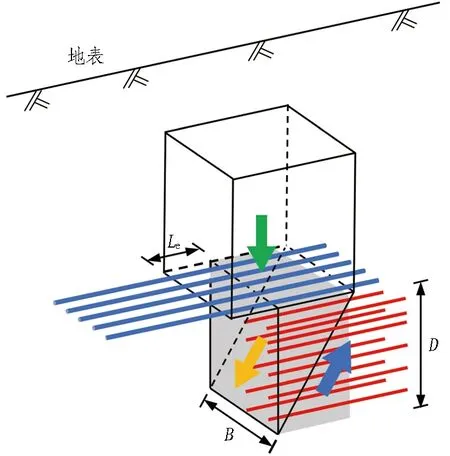
(a) 轴测图

假设围岩为满足Mohr-Coulomb强度准则的理想刚塑性材料。掌子面受力模式如图2所示。

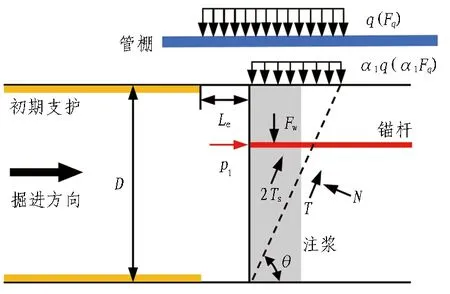
θ为破坏面与水平方向的夹角； T为掌子面前方滑动面切向摩阻力; Ts为两侧滑动面切向摩阻力; N为前方滑动面法向作用力; Fq为围岩压力合力; Fw为掌子面滑移体自重; p1为掌子面锚杆支护力; α1为超前管棚传力系数。

根据极限平衡法，定义隧道掌子面稳定系数

(1)

式中:F1、F2分别为沿掌子面前方滑动面方向的抗滑力和下滑力。

根据掌子面水平、竖向静力平衡条件，得：

p1+(T+2Ts)cosθ=Nsinθ；

(2)

α1Fq+Fw-(T+2Ts)sinθ=Ncosθ。

(3)

根据掌子面几何参数(如图1和图2所示)，得：

Fq=qB(Dcotθ+Le)；

(4)

(5)

式(4)—(5)中：q为围岩压力;γ为围岩重度。

根据文献[19]，Ts的计算公式为

(6)

式中:α2为掌子面预注浆加固后围岩黏聚力增大系数；c为黏聚力;λ为围岩侧压力系数；φ为内摩擦角。

为了消去T和Ts，将式(2)乘以sinθ、式(3)乘以cosθ后相加，得

N=(α1Fq+Fw)cosθ+p1sinθ。

(7)

根据线性Mohr-Coulomb准则，得

(8)

沿滑动面切向分解各力，得：

F1=T+2Ts+p1cosθ；

(9)

F2=(α1Fq+Fw)sinθ。

(10)

联立式(1)—(10)，得

(11)

其中：

(12)

(13)

β3=cotθ·tanφ;

(14)

(15)

(16)

式(11)—(16)中：Fc为掌子面前方及两侧滑动面黏聚力合力；Fφ为掌子面两侧摩擦力合力；β1、β2、β3为与φ相关的系数,为考虑超前支护措施对掌子面破坏模式的影响，取0°<θ<90°范围内K的最小值作为掌子面稳定系数；p1、α1、α2的计算方法及超前支护体系设计流程参考文献[20]。

2 基于BQ系统的隧道洞身形变压力计算方法及支护结构设计模型

2.1 BQ系统

在GB/T 50218—2014《工程岩体分级标准》[21]中，岩体基本质量指标BQ由岩石饱和单轴抗压强度(Rc)和岩体完整性指数(Kv)共同决定。基于153组样本数据，采用数理统计分析方法，建立岩体基本质量指标BQ的计算公式为

BQ=100+3Rc+250Kv。

(17)

采用GB/T 50218—2014《工程岩体分级标准》[21]对地下工程岩体进行分级时，需要对岩体基本质量指标(BQ)进行修正。主要修正指标有3项，即地下水影响修正系数(K1)、主要结构面产状影响修正系数(K2)和初始应力状态影响修正系数(K3)。最终，将地下工程岩体基本质量[BQ]的计算公式修正为

[BQ]=BQ-100(K1+K2+K3)。

(18)

通过BQ围岩分级系统将我国岩体基本质量划分为5个等级，见表1。

表1 岩体基本质量分级[21]

2.2 洞身围岩稳定性设计模式

通过现场实测形变压力[6]及文献[22]可知，Ⅱ级和Ⅲ级及部分Ⅳ级和Ⅴ级围岩支护结构受局部荷载作用较为明显，Ⅳ级和Ⅴ级围岩支护结构受拱形荷载作用较为明显。局部塌方和拱形塌方示意图见图3。

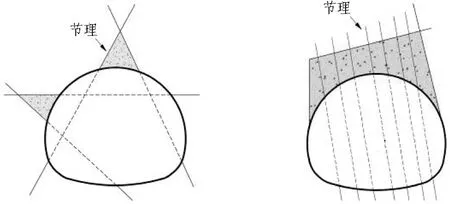
(a) 局部塌方 (b) 拱形塌方

故针对不同围岩等级支护结构所受荷载模式的不同，提出整体形变压力计算方法及局部形变压力计算方法，并提出对应的支护结构设计模型。

2.3 整体形变压力计算方法及支护结构设计模型

本文通过获取大量的现场实测样本数据，采用数理统计方法，建立基于BQ值的形变压力计算方法。为了保证数据的丰富性及分析结果的合理性，本次样本除获取机械化施工隧道(郑万高铁隧道)的监测数据外，还收集整理了其他国内较为典型的隧道的监测数据。样本包括国内44座隧道、205个断面形变压力监测数据，主要分布在我国华北、华中、华东、华南以及西南地区，具有一定的代表性。通过多元非线性回归分析，以GB/T 50218—2014《工程岩体分级标准》[21]围岩BQ值分级为依据，提出隧道BQ法形变压力计算公式为：

q=0.33γ(0.2+0.1B)exp(-0.006BQ+4.2)。

(19)

e=2.7exp(-0.006 6BQ)q。

(20)

式中：q为竖向形变压力；e为水平向形变压力。

为了将提出的BQ法形变压力计算公式与RMR系统、Q系统形变压力计算公式进行对比分析，根据BQ、Q、RMR值三者之间的转化关系，建立以BQ值为变量的Q系统、RMR系统形变压力计算公式。具体过程如下：

1)根据已有研究成果可知，RMR值与BQ值存在如式(21)所示的转化关系[23]，Q值与RMR值存在如式(22)所示的转化关系[13]，进而可得到Q值与BQ值之间的相互转化关系(见式(23))。

RMR=(BQ-80.79)/6.09。

(21)

Q=exp[(RMR-44)/9]。

(22)

将式(21)代入式(22)，可得

Q=exp[(BQ-348.75)/54.81]。

(23)

2)将RMR系统、Q系统形变压力计算公式[12-13]中的RMR值和Q值用BQ值代替，得到以BQ值为变量的RMR系统、Q系统形变压力计算公式。

(24)

(25)

式(24)—(25)中：H为隧道埋深；Jr为围岩节理粗糙度系数。

通过控制变量法，分析对比了RMR系统、Q系统、BQ系统下形变压力的变化规律，分析结果如图4所示。

由图4可知： 各形变压力计算方法考虑因素不一，变化规律及量值也存在较大差异；Q系统的形变压力对Q值及Jr较为敏感，RMR系统的形变压力计算方法对RMR值、隧道埋深及隧道跨度较为敏感，而BQ系统的形变压力对BQ值及隧道跨度较为敏感。由于各形变压力计算方法均为根据现有资料统计分析得出，代表了各国的实际地质环境及施工技术情况，可借鉴，但不能直接套用。

对于Ⅳ级和Ⅴ级软弱围岩，喷射混凝土和围岩之间的黏着力较小，支护结构一般受径向均布荷载作用，此时，可以按整体计算模型进行设计。模型中喷射混凝土可以作为梁单元，根据围岩条件确定荷载大小，考虑到喷射混凝土与围岩有一定的黏着力，采用径向、切向弹簧来模拟喷射混凝土与围岩之间的抗拉、抗剪作用。整体支护结构设计模型如图5所示。根据以上整体计算模型，可以计算获得梁单元内力、弹簧抗力等。对于梁单元，根据内力计算出梁单元安全系数，据此可以判定梁单元的安全性，并进行喷射混凝土厚度设计。

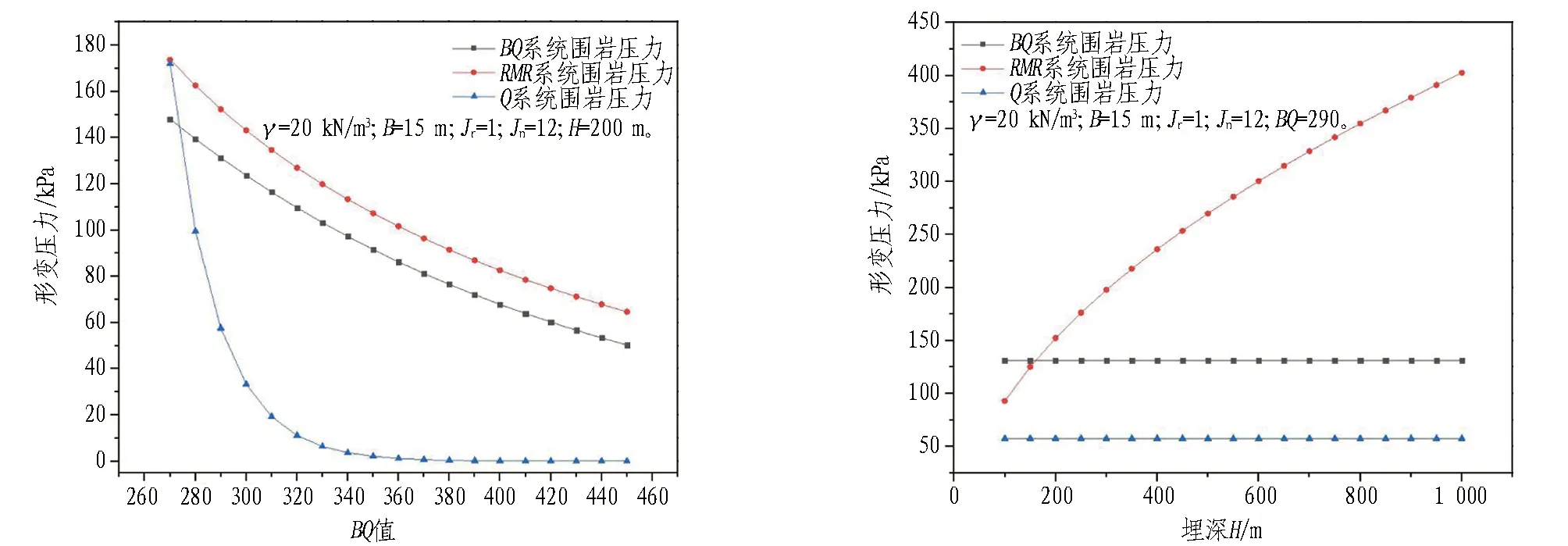
(a) 形变压力随BQ值的变化规律

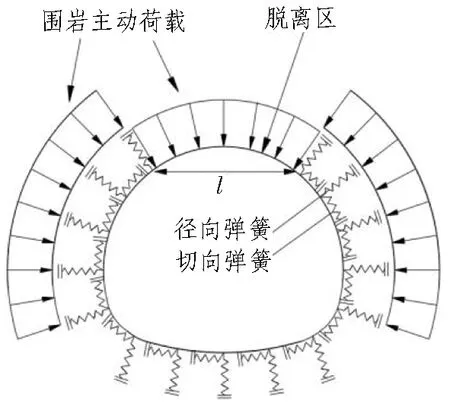
图5 整体支护结构设计模型

2.4 局部形变压力计算方法及支护结构设计模型

通过对现场实测形变压力数据进行分析，基于整体形变压力计算公式，建立了局部形变压力计算方法。

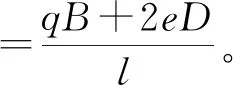
(26)

(27)

q局=ηq径。

(28)

式(26)—(28)中：η为局部最大荷载(qmax)与径向均布荷载(q径)的比例系数，可由统计分析得到；l为荷载作用范围;q局为局部荷载。

对于Ⅱ级和Ⅲ级围岩，喷射混凝土能够与围岩壁面大面积黏附，是一种有效的支护手段，其作用主要来自喷射混凝土与围岩壁面的黏着力所产生的抗剪阻力，由此建立局部计算模型，如图6所示。模型中，喷射混凝土可以作为梁单元，根据围岩条件确定荷载大小和作用范围，考虑到喷射混凝土与围岩有较强的黏着力，荷载作用范围外的两端一定长度范围内，可以采用径向、切向弹簧来模拟喷射混凝土与围岩之间的抗拉、抗剪作用，最外端可按固定支座处理。

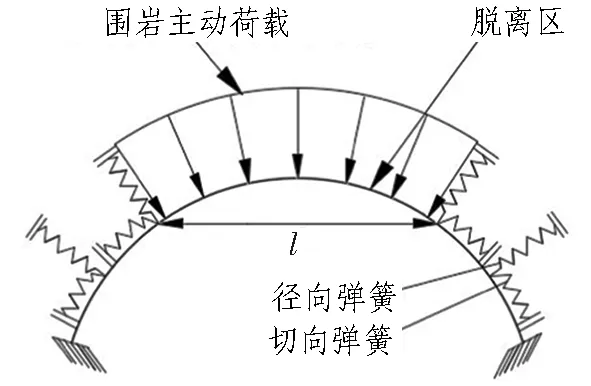
图6 局部支护结构设计模型

3 工程应用

郑万高铁湖北段是我国高速铁路隧道全地质(Ⅱ—Ⅴ级围岩)、全断面实施机械化施工的先行者，目前已在18座隧道(47个工区)实现了大型机械化全断面工法，相关研究成果[2-6]为我国隧道工程施工技术的发展奠定了坚实的基础。

3.1 郑万高铁隧道掌子面超前支护参数

基于本文的超前支护设计方法，提出郑万高铁隧道掌子面超前支护参数(见表2)，通过现场1 115个掌子面的系统应用，证明了该参数的合理性及本文设计方法的实用性。其中，围岩力学参数取值参考TB 10003—2016《铁路隧道设计规范》[24]，工法说明参考文献[5]。

表2 郑万高铁隧道掌子面超前支护参数

3.2 郑万高铁隧道初期支护参数

基于本文建立的隧道洞身形变压力计算方法(BQ法)及支护结构计算模型(荷载-结构模型)，提出郑万高铁隧道初期支护设计参数(见表3)，初期支护安全系数如表4所示。最终将该洞身支护结构设计参数应用到郑万高铁湖北段隧道群中，并通过对现场13座隧道、101个监测断面结构受力、结构变形的监测数据进行分析，可知各监测断面均处于安全状态，进一步验证了本文所提隧道洞身支护结构设计方法的合理性。其中，围岩及支护结构力学参数取值参考TB 10003—2016《铁路隧道设计规范》[24]。

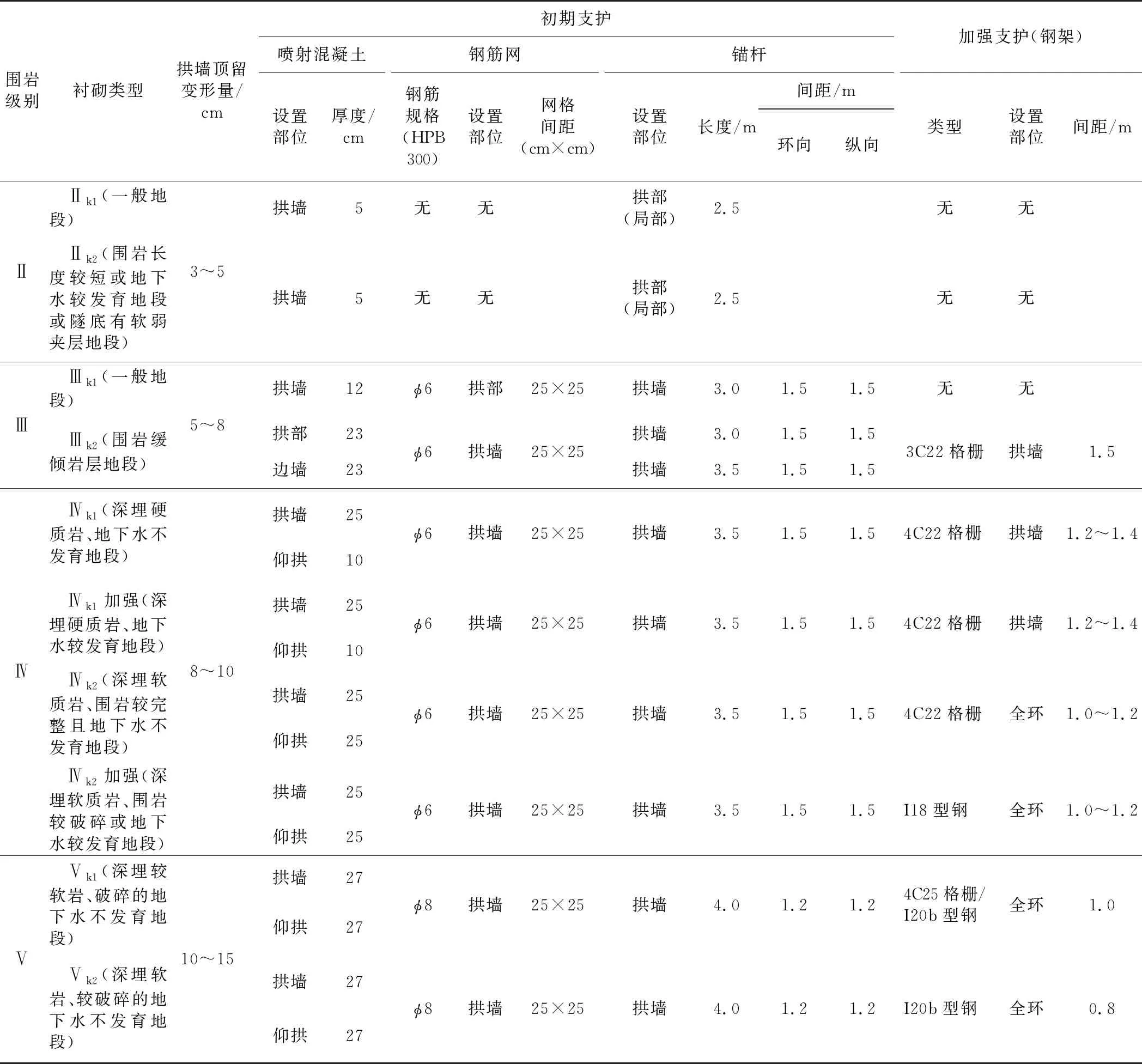
表3 郑万高铁隧道初期支护参数

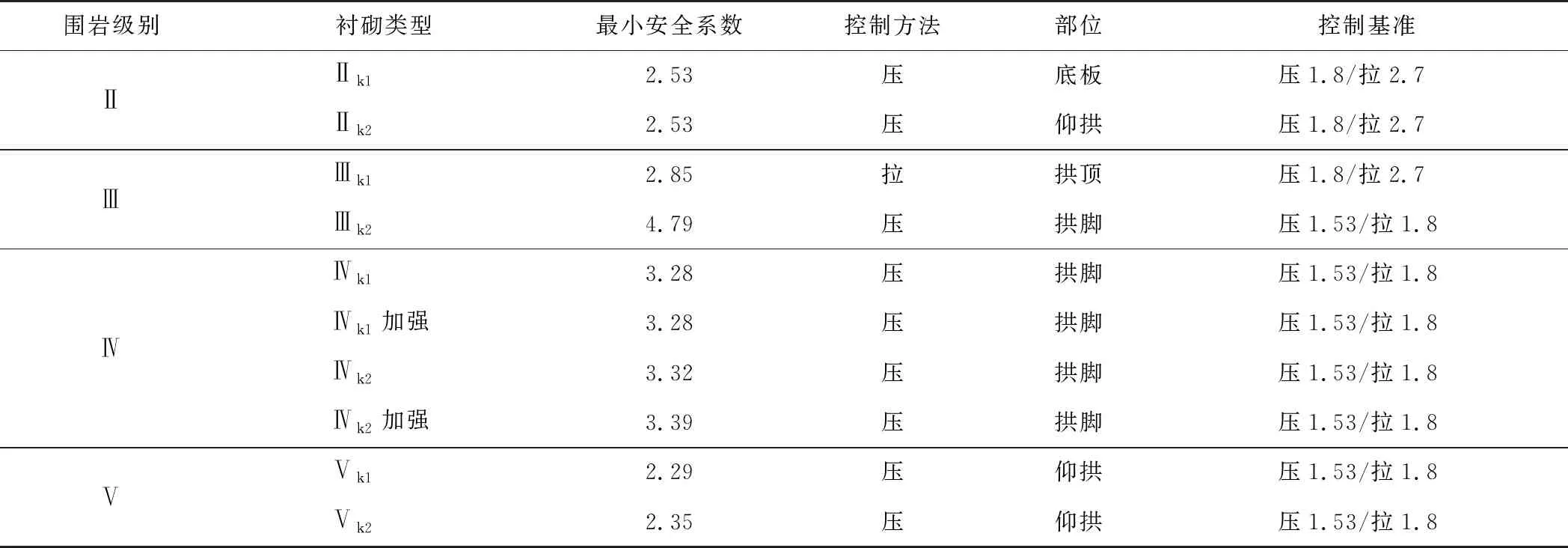
表4 初期支护安全系数

4 结论与讨论

本文提出了一种考虑超前管棚、掌子面锚杆、掌子面预注浆等3种加固措施的隧道超前支护设计方法。基于形变压力现场实测数据，拟合推导了基于BQ系统的形变压力计算公式，建立了洞身支护结构设计模型，并通过工程应用证明了本文设计方法的合理性。然而，仍存在以下问题：

1)为了简化计算方法，掌子面稳定性分析模型中的各子部分均采用了一些假设条件，且部分假设条件难以验证，导致计算结果的误差难以估计；因此，在今后的研究中需要减少假设条件，建立更为合理的计算模型。

2)形变压力与围岩应力状态、时间、支护刚度等因素相关，但由于测试数据的局限性，本文并未考虑时间和支护刚度的影响；因此，在今后的研究中需要更广泛地开展形变压力现场测试，进一步完善形变压力计算公式。

3)本文提出的形变压力整体及局部计算模式，为与现存支护结构设计参数检验方法相配套，近似地采用了松动压力的计算模式，且其中的相关计算参数做了一定的简化，计算结果存在一定的误差；因此，在今后的研究中应进行深入分析，减少相关假设条件，建立更合理的计算模型。