基于层次分析法-模糊综合评价法的盾构掘进适应性评价
2021-02-24张瑉嘉张家铭尚玉杰
姜 伟,杨 磊,石 强,张瑉嘉,张家铭,尚玉杰
(1.中国水利水电第七工程局有限公司,成都 610213;2.中国地质大学(武汉)工程学院,武汉 430074)
近年来,中国经济迅猛发展,城市化步伐加快,城镇人口密度急剧增大,由此导致的城市交通拥堵问题愈发突出,而地铁以其运输量大、快捷准时、绿色环保等特点成为缓解城市交通压力的理想选择[1]。目前用于盾构隧道施工的方法主要包括明挖法、浅埋暗挖法、盾构法等,其中盾构法以其对环境危害小、施工质量高、速度快、安全等优势,被广泛应用于地铁隧道建设中。地铁建设往往投资巨大、施工环境复杂,若对盾构掘进的适应性分析不够,很可能会在施工中遇到很大困难,造成工期延误,资源浪费。因此,盾构掘进适应性的研究对保证盾构施工顺利进行、控制盾构隧道施工成本具有十分重要的意义。
目前,中外学者对盾构掘进适应性做了大量的研究,主要集中在盾构选型、模型试验、掘进参数、风险分析等研究方向。如丁志诚等[2]分析了影响盾构选型的因素,提出盾构选型的流程,并对不同地层的切削机理进行了阐述;Edalat等[3]采用多标准分析法为盾构机械选型;吴贤国等[4]基于接近理想点(technique for order preference by similarity to an ideal solution,TOPSIS)法确定了盾构选型流程,利用主客观赋权法确定指标权重,提出了盾构选型的评价方法。Champan等[5]通过螺旋出土器研究了双孔盾构隧道的开挖;刘纪峰等[6]通过模型试验,研究了考虑土-水耦合的地表沉降规律;夏光辉等[7]通过室内模型试验分析了盾构隧道施工对临近基坑围护结构的影响效应;朱合华等[8-10]通过室内模型试验研究软土地层中盾构适应性问题及参数之间的影响关系。在对盾构掘进参数进行研究时,一般选取能够反映盾构掘进控制与掘进状态的关键参数,采用数理统计方法[11]、对比分析方法[12-13]、误差逆传播(back propagation,BP)人工神经网络方法[14]研究掘进参数对盾构施工的影响,为参数选取和优化提供指导。潘茁等[15]通过高频率采集数据,采用数理统计的方法对扭矩和盾构施工引起的土体位移的相关性进行了讨论。盾构施工风险分析一直是盾构掘进适应性研究的重要内容。黄俐等[16]采用案例分析的方法对北京地铁6号线盾构施工的风险进行了分析;陶洋等[17]从统计学角度出发,提出因子分析和BP神经网络相结合的分析方法,为成本风险分析提供了新思路;陈建福[18]以厦门轨道2号线跨海段盾构隧道为依托,针对特定工程问题,提出了盾构适应性的总体要求。
现有文献中关于盾构掘进适应性的研究多针对特定的工程,且以定性分析为主,而对系统的盾构掘进适应性评价体系研究较少,无法对盾构掘进的适应性做定量评价,限制了评价结果的客观性、准确性。鉴于此,现联合运用模糊综合评价法和层次分析法(analytic hierarchy process,AHP),构建盾构掘进适应性定量评价模型,并以深圳地铁12号线某标段为例,结合实际情况,构建模糊综合评价体系,对盾构掘进适应性进行定量评价。
1 AHP-模糊综合评价模型
在对实际问题进行评价时,信息与数据往往具有模糊性(不确定性),无法进行精确划分,这阻碍了人们对模糊信息的处理。基于此,Zadeh[19]于1965年提出了模糊集的概念,用精确的数学方法处理模糊现象,这标志着模糊数学的诞生。模糊综合评价法以模糊数学为基础,其基本思想是将评价目标根据影响因素进行分解,构造评价指标体系并赋值确定权重,通过模糊集合变换原理,以隶属度描述各指标及其模糊界限,构造模糊矩阵,通过复合运算,确定评价目标的可靠性。权重是通过数量对比,权衡被评价目标总体中各指标相对重要程度的量化值,其确定方法有多种,包括统计法、专家调查法、AHP法等。AHP法作为一种处理多目标决策的定量与定性相结合的理论方法,所需数据量少,评分花费时间短,计算工作量小,便于理解掌握,计算准确性较好,被广泛应用于指标权重的确定[20-21]。AHP与模糊综合评价法的联合使用可对盾构掘进适应性进行定量评价。
确定评价指标体系是进行适应性评价的关键。建立科学合理的评价指标体系要视具体问题而定,一般来说,要遵循层次性、效度、简明性等原则。层次性原则指评价指标的选取要从整体层次上把握评价目标协调,保证评价指标全面性、科学性;效度原则指评价指标的选取要分清主次,具有代表性;简明性原则指评价指标要简单、明了、便于操作,且具有代表性[22-23]。
1.1 AHP法确定权重
AHP法是将与决策问题按一定原则条理化,构成完整的结构模型,在此基础上进行定性定量分析的方法。其具体步骤[20]如下。
(1)建立递阶层次模型。将决策问题层次化,构造有层次的结构模型,将其分解成目标层、准则层、方案层三个层次。
(2)构造判断矩阵。采取因子两两比较建立矩阵的办法,以bij表示影响因素指标Bi和Bj对目标A的影响,同理,1/bij表示Bj和Bi对目标A的影响,建立矩阵B=(Bij)n×n,Bij的确定采用1~9及其倒数作为标度,其赋值标准如表1所示。

表1 判断矩阵中标度赋值标准[24]Table 1 The evaluation standard of elements in judgment matrix[24]
(3)层次单排序及一致性检验。将判断矩阵B对应于最大特征值λmax的特征向量,经归一化后,可得到同层次相应因素对上一层次某因素相对重要性的排序权值,即为层次单排序。
判断矩阵的一致性检验需计算一致性指标(CI、RI)及一致性比例(CR),当CR<0.1时,认为判断矩阵的一致性是可以接受的。CI、RI及CR的计算公式为

(1)
式(1)中:λ′max为采用随机方法构造的500个样本矩阵,并随机从1~9及其倒数中抽取数字构造正互反矩阵的最大特征值的平均值。
(4)层次总排序及一致性检验。基于层次单排序的结果将权重进行合成,得到各因素对总目标的排序权重。
1.2 模糊综合评价法
1965年,Zadeh[19]提出将客观世界里存在的模糊概念纳入数学的应用范畴。这些模糊概念通过微积分、线性代数、数理统计和概率论等精确数学方法处理后,可使其具有数学的共性,进行定量评价分析。模糊数学不是让数学变得模糊,而是将模糊概念定量化。模糊综合评价法是一种以模糊数学为基础,针对评价目标,构造评价体系及隶属函数,通过模糊集合论的相关运算和变化,对模糊对象进行定量评价的分析方法。具体步骤[25]如下。
(1)建立因素集。因素集为影响评价对象的因素构成的集合,记为
U={u1,u2,…,um}
(2)
式(2)中:ui(i=1,2,…,m)为各影响因素,常具有不同程度模糊性;m为影响因素的个数。
(2)建立评价集。评价集为对评价对象可能做出的评价结果的集合,记为
V={v1,v2,…,vn}
(3)
式(3)中:vi(i=1,2,…,n)为评价指标,一般用模糊语言描述,在模糊数学中用[0,1]间取值的隶属函数量化。采用的三角形、偏小型、偏大型分布分别为

(4)
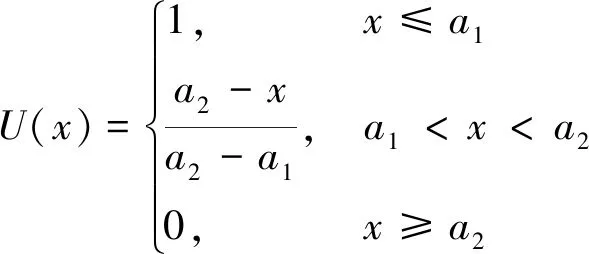
(5)
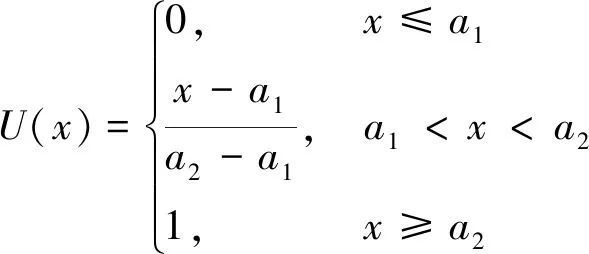
(6)
(3)单因素评价。确定因素集对评价集的隶属度,构成单因素评价矩阵,记为

(7)
(4)确定各因素权重集。权重指表征各因素对应重要性大小的值,记为
A={a1,a2,…,am}
(8)
ai归一化后,有

(9)
(5)模糊综合评价。将因素集上的模糊集合通过模糊变换为评语集上的模糊集合,即为模糊综合评价。其模糊变换式为

(10)
式(10)中:C为评语集上的等级模糊子集;ci(i=1,2,…,n)为等级模糊子集的隶属度。
比较各因素隶属度的大小情况,根据最大隶属度原则,最大数为被评价对象最有资格属于的等级。
2 AHP-模糊综合评价法应用实例
2.1 工程概况
深圳地铁12号线某区间右线设计起点为YCK14+750.648,设计终点为YCK15+663.153,长度为912.505 m;左线设计起点为ZCK14+750.586,设计终点为YCK15+663.153,长度为912.512 m(短链0.004 m)。拟采用土压盾构法施工,顶板埋深7.1~17.6 m。线路两旁多为厂房、民宅、商用建筑。地铁沿线穿越地层包括第四系全新统人工堆填层(Q4ml)、全新世海冲积层(Q4m)、全新世海陆交互相冲积层(Q4mc)、全新世冲洪积层(Q4al+pl)、晚更新世冲洪积层(Q3al+pl)、坡积层(Qdl)、残积层(Qel),下伏基岩为燕山第四期粗粒花岗岩(γ53)。隧道穿越的地层主要为花岗岩(最大岩石强度130 MPa)、砾质黏性土、粉质黏土、淤泥、含泥中粗砂等。区间地层剖面如图1所示。
盾构机最大开挖直径6.44 m,所采用的管片由3块标准管片+2块邻接管片+1块封顶块组成,错缝拼装,弯螺栓连接。管片外径6.2 m,内径5.5 m,宽度1.5 m,厚度35 cm。盾构机主机长度约9 m,整机长度85 m,重约530 t,装机功率约1 850 kW(仅设备上)。所用土压盾构机如图2所示。图3为管片拼装过程。
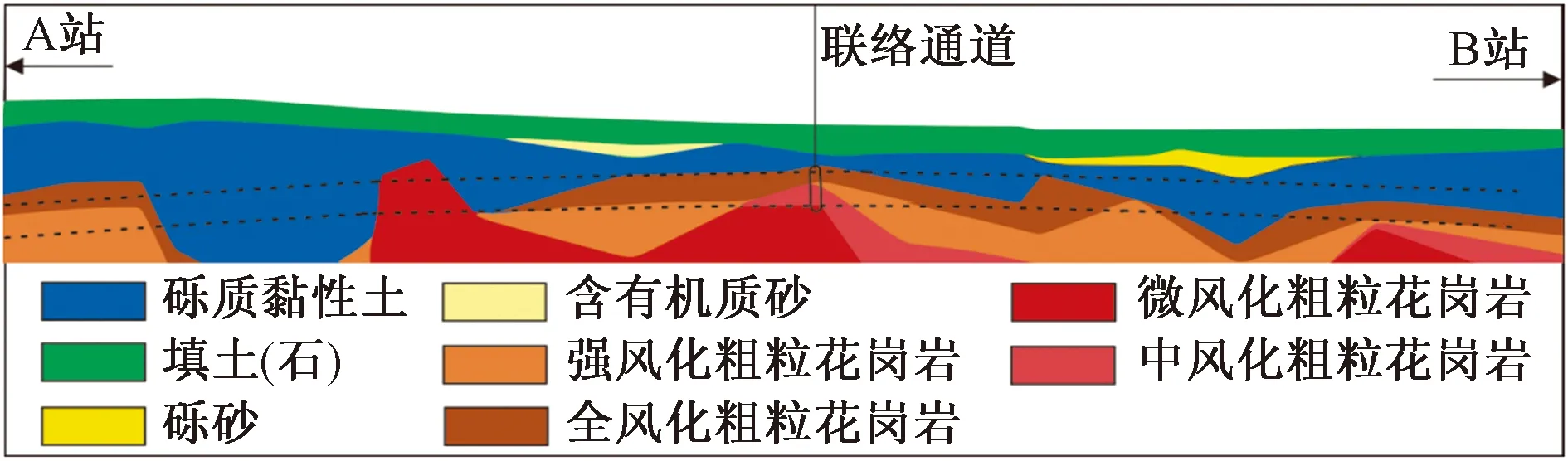
图1 研究区域地层剖面图Fig.1 Stratigraphic profile of study area

图2 土压平衡盾构机Fig.2 Earth pressure balance shield machine

图3 管片拼装Fig.3 Segment assembly
2.2 适应性评价指标的选取及权重确定
通过调研国内外相关资料、向专家及经验丰富的从业人员发放调查问卷的方式,选取了三大类11项盾构掘进适应性评价的指标,确定了目标层—准则层—指标层判断矩阵,并进行了一致性检验,如表2~表7所示。
总排序的一致性比例为
层次总排序的一致性比例CR<0.1,说明排序具有较好的一致性。

表2 土压平衡盾构适应性评价指标及其物理量纲Table 2 The evaluation index and physical dimension of earth pressure balance shield adaptability

表3 目标层—准则层判断矩阵A-BTable 3 Target layer—rule layer judgment matrix A-B
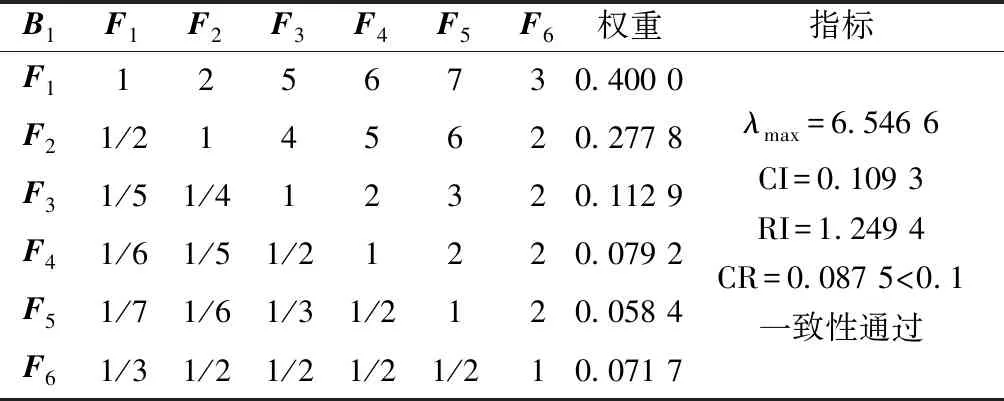
表4 “盾构设计”对指标层的判断矩阵B1-FTable 4 “Shield design” to scheme layer judgment matrix B1-F
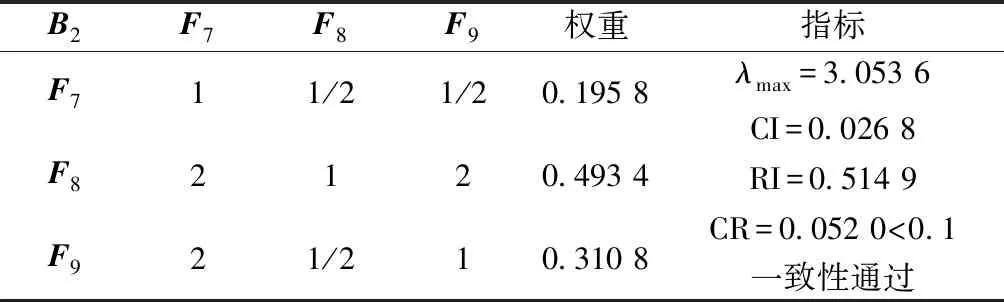
表5 “地质条件”对指标层的判断矩阵B2-FTable 5 “Geological conditions”to scheme layer judgment matrix B2-F
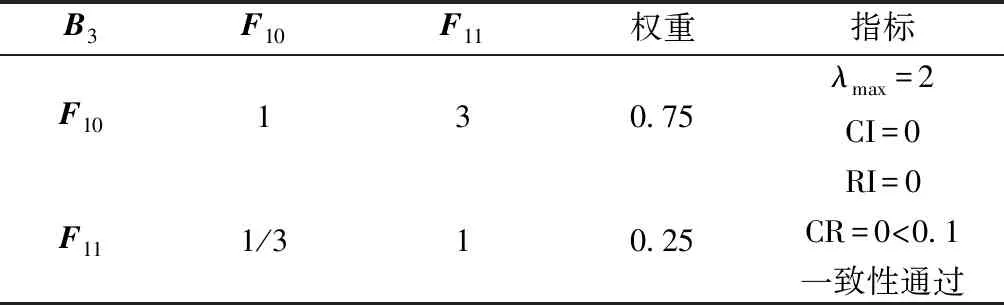
表6 “施工组织”对指标层的判断矩阵B3-FTable 6 “Construction organization” to scheme layer judgment matrix B3-F

表7 层次总排序计算表Table 7 The total sorting table
2.3 评价指标隶属函数的确定
盾构掘进适应度的确定往往涉及多项指标,其属性、单位、重要性各异存在着模糊性。因此,为消除模糊性,构建了隶属函数进行定量化的评价。用[0,1]的数值表示不同的适应程度,0表示完全不适应,1表示完全适应,并采用线性关系确定隶属函数值。各评价指标计算方法及针对工程条件确定的评价标准如表8所示。根据评价标准,构建各评价指标隶属函数如表9所示。
2.4 评价指标数据
根据工程实际条件,列出如表10所示适应性评价指标数据。
2.5 模糊综合评价
根据模糊综合评价式(9)对盾构掘进适应性进行评价,计算如下。
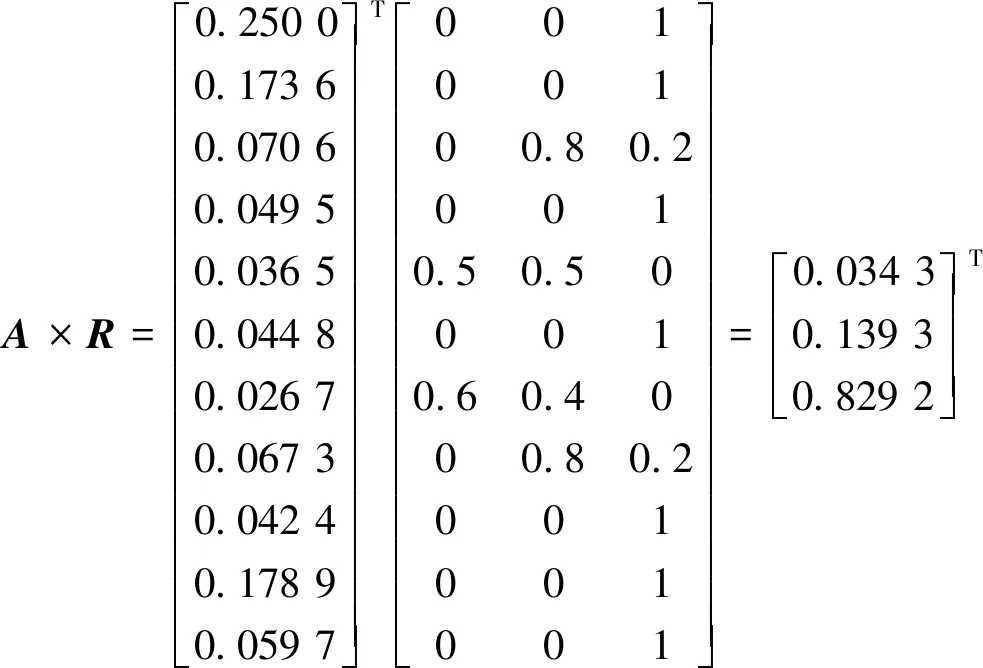
计算结果{0.034 3,0.139 3,0.829 2}分别表示盾构掘进对应于不适应、基本适应、适应的隶属度。其中,最大隶属度数值为0.829 2,根据最大隶属度原则,此区间盾构掘进适应性为适应。

表8 评价指标的计算方法及评价标准Table 8 The evaluation index calculating method and evaluation standard

表9 评价指标隶属函数Table 9 The membership function of evaluation index
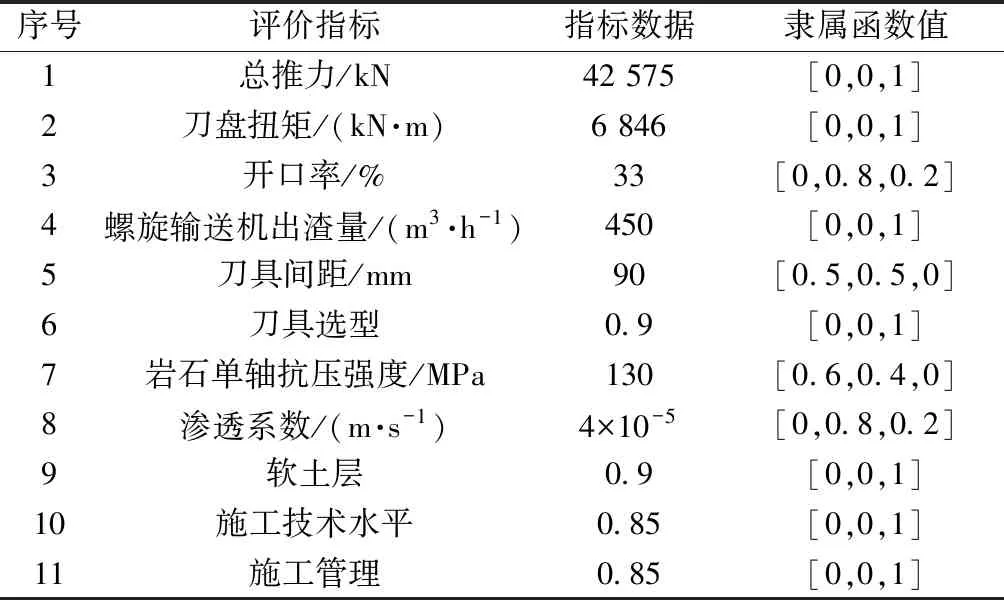
表10 适应性评价指标数据及隶属函数值Table 10 The adaptability evaluation index data and membership function values
3 结论
提出联合运用模糊综合评价法和AHP法对盾构掘进适应性进行评价的方法,并结合工程背景,构建模糊综合评价模型,对深圳地铁12号线某区间工程盾构掘进适应性进行评价,得出如下结论。
(1)采用AHP法和模糊综合评价法,对盾构掘进适应性进行定量评价,既发挥了专家经验的作用,又减少了人为主观臆断导致的误差,提高了评价结果的客观性和准确性。
(2)结合工程背景对深圳地铁12号线某区间工程盾构掘进适应性进行评价,盾构掘进适应性为适应,为类似工程提供一定借鉴作用。
(3)在实际工程应用中,要根据特定条件,确定评价指标因素及权重,提高评价结果的客观准确性。
