分数阶耦合电感的无源性

马 龙,王 璐,梁贵书

(1.华北电力大学电力工程系，保定 071003；2.华北电力大学科技学院，保定 071051)

近年来，分数阶微积分理论的发展为人们提供了一种解释复杂现象和动态系统的强大工具，其特有的对于“in between”特性以及记忆特性的描述能力，使其在黏弹性、控制、分形、信号分析处理等方面广泛应用[1]。在电气工程领域，学者指出实际存在的电容、电感均存在分数阶效应[2]；导体高频体现出的集肤效应可以用0.5阶分数阶微积分来描述；硅钢片等需要用0.5阶系统进行准确描述；现有的DC-DC变换器[3]、超级电容器[4]、传输线、电缆[5]等器件和设备使用分数阶微积分建模能够获得更高的精度[6-7]。目前，电力电子器件的分数阶建模正在成为研究热点。

为了方便地表征分数阶微积分，在建模过程中提出了分抗[8](fractance)的概念。该类元件通过在赋定关系中引入电压或(和)电流的非整数阶微分和积分，极大地拓展了传统的电路元件范畴。当分抗元件的阶次分别取为0、+1和-1时，该元件就退化成已有的整数阶电阻、电感和电容。为了应用方便，学者们又提出了分数阶双口元件[9]、分数阶耦合电感以及众多含分数阶元件电路[11-18]，包括分数阶次的RLC电路、振荡器、滤波器和控制器等。此外，学者们对传统的电网络理论也进行了相应的拓展，探索研究了分数阶网络的灵敏度分析方法[19]和分数阶网络综合方法[6,20-23]。

作为一类重要的电路元件，整数阶耦合电感在各类测量仪器、通信系统、控制系统、信号处理、设备建模、模拟滤波器等方面应用广泛，耦合电感在各领域的应用能够显著提高设计的灵活性和系统的性能[24-25]。同时，整数阶耦合电感也是无源电路综合的重要组成部分。最近，考虑实际电感元件的非理想特性以及射频领域内耦合电感阶次明显小于1的特性，文献[10]提出了分数阶耦合电感(fractional mutual inductors,FMI)的概念及实现方法，并以双调滤波器为例对其特性进行了研究；文献[26]研究了FMI的阻抗和相位特性并将其应用在无线电能传输领域；文献[27]讨论了含FMI网络的灵敏度分析方法。文献[28]提出了一种大功率分数阶电感电路的等效模型，并应用到并联谐振电路中。目前，学者们正在积极探索分数阶元件的产业化，但分数阶元件的互易性及无源性鲜有研究。

在电路分析和综合理论中，无源性这一术语用以描述元件或网络吸收能量的特性[29]。一方面，无源网络具有很多优异的特性，已经推导证明了无源网络的诸多结论，例如：线性无源网络一定是稳定的；由无源元件构成的网络无源等；另一方面，无源性也是无源电路综合的重要前提。因此开展FMI的无源性证明意义重大。

现从频域角度入手，首先介绍广义坐标和耗散矩阵的定义，然后借助耗散矩阵的概念，推导获得FMI的无源性条件，并通过实例对其无源性条件进行说明。分数阶耦合电感的提出进一步丰富和完善了已有的电路元件体系，开展该类分数阶元件的无源性研究将促进相关的电路分析和综合理论的发展。

1 FMI元件定义

1.1 分数阶微积分

分数阶积分定义[1]为

(1)

式(1)中：D-α为分数阶微分算子；α为任意正数；Γ(·)为欧拉伽玛函数。

Caputo分数阶微分定义[1]为

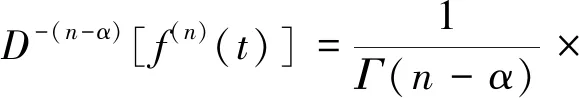
(2)

式(2)中：n-1<α≤n；Dα为分数阶微分算子；函数f的n阶导数f(n)在区间[a,t]可积。

1.2 FMI元件

FMI的符号表征如图1所示，其定义式[8]为

(3)

对应的频域形式为

(4)

图1 FMI符号表征Fig.1 Notation of FMI

当γ1=γ2=β=α时，式(4)描述了一类特殊的FMI，即

(5)

图2所示为互易FMI的电路符号。

图2 互易FMI符号表征Fig.2 Notation of reciprocal FMI

2 FMI的无源判据

从频域角度入手，首先介绍广义坐标和耗散矩阵的概念，并以此为基础推导获得FMI的无源条件。

2.1 广义坐标与耗散矩阵

定义1n口元件的广义坐标[25-26]ξ和θ为

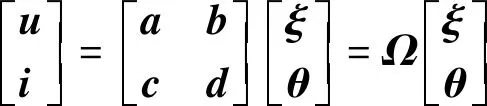
(6)

(7)

定义2n口元件的耗散矩阵[25-26]定义为

D(s)=[cΛ(s)+d]H[aΛ(s)+b]

(8)

式(8)中：Λ(s)为元件的赋定矩阵，即满足

Ξ(s)=Λ(s)Θ(s)

(9)

引理1 线性元件N无源等价于矩阵D(s)+DH(s),对于一切右半开平面内的s为半正定矩阵[27-28]。

引理2 将引理1结论分别应用于网络的阻抗参数矩阵Z、导纳参数矩阵Y、混合参数矩阵H、传输参数矩阵T和散射参数矩阵S时，可得到相应的等效无源判据[27-28]，即

(1)Z(s)+ZH(s)半正定。

(2)Y(s)+YH(s)半正定。

(3)H(s)+HH(s)半正定。

(4)I-S(s)SH(s)半正定。

需要指出，将引理1和引理2进行分数阶拓展，上述定理仍然成立。

2.2 FMI的无源性条件

定理1 由式(3)和式(4)定义的FMI无源条件为

α+β=2γ1=2γ2

(10)

L11≥0,L22≥0

(11)

(12)

(13)

证明：对式(4)所述的FMI，可以方便地获得其阻抗表征为

(14)

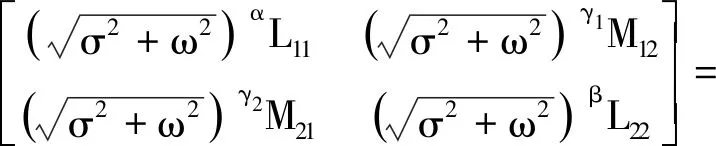
(15)

对ZF(s)取共轭转置，得到其厄尔米特阵为

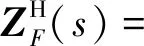
(16)

因此，有

(17)

式(17)中矩阵对右半开平面内的一切s为半正定矩阵的条件[27]为

L11Aαcos(kα)≥0

(18)

L22Aβcos(kβ)≥0

(19)

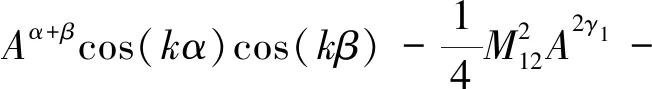
kγ2)≥0

(20)

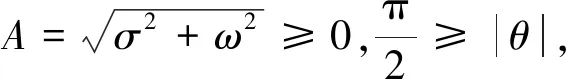
α+β=2γ1=2γ2

(21)

否则，取ω=0，σ≥0，故θ=0，A=σ，式(20)变为

即

(22)

可以得到：

考虑式(21)，对式(20)进行简化可得

L11cos(αθ)≥0

(23)

L22cos(βθ)≥0

(24)

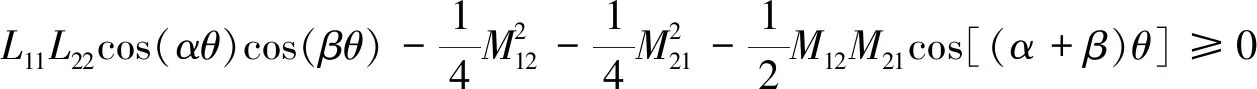
(25)

由式(25)可知，F(θ)是θ的偶函数，故可仅考虑[0,π/2]区间内的情况。使用积化和差公式，F(θ)可等价表征为

(26)

式(25)在θ=0时成立，可得

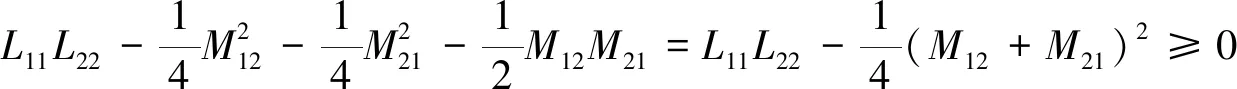
(27)

对式(27)求导可得

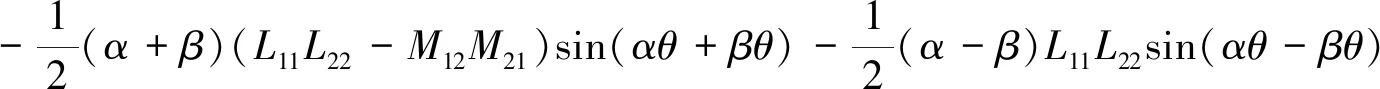
(28)

由式(28)可知，在满足式(26)的条件下，函数F(θ)在区间[0,π/2]单调减小。故此时再保证θ值取为π/2时F(θ)≥0成立即可。从而可得到式(10)～式(13)给出的无源条件。

证毕。

(1)对互易FMI，其无源条件变为

α+β=2γ，1≥α,β≥0；

L11≥0，L22≥0；

L11L22-M2≥0；

(2)对由式(5)定义的同元次FMI，其无源性条件为

L11≥0,L22≥0，1≥α≥0；

需要指出，传统整数阶耦合电感对应式(14)中的分数阶次参数均为1，此时式(10)给出的条件自然满足，由式(11)～式(13)推导可得整数阶耦合电感的无源条件为

L11≥0,L22≥0；

即L11≥0，L22≥0，M12=M21=±M，且L11L22-M2≥0，与已有结论相一致。

3 FMI的无源判据

例1 讨论无源FMI一二次侧线圈串联和并联所得电路(图3)的无源性。

图3 无源FMI同名端电路Fig.3 Circuit of a passive FMI

当无源FMI按图3(a)所示方式进行连接时，有I1(s)=I2(s)，U(s)=U1(s)+U2(s)，得到其阻抗表达形式为

Zs=sαL11+sβL22+sγ1M12+sγ2M21

(29)

当无源FMI按图3(b)所示方式进行连接时，有U1(s)=U2(s)，I(s)=I1(s)+I2(s)，可知其导纳表达形式为

(30)

式(30)中：Δ=L11L22-M12M21。

由于该FMI无源，可知其满足定理1中式(10)～式(13)给出的条件。因此，Zs的实部可以表达为

Re(Zs)=AαL11cos(αθ)+AβL22cos(βθ)+

(31)

式(31)中：θ∈[-π/2,π/2]。由于Re(Zs)为变量θ的偶函数，故可仅考虑[0,π/2]内Re(Zs)的符号。对式(31)右侧前两项，使用重要不等式可得

(32)

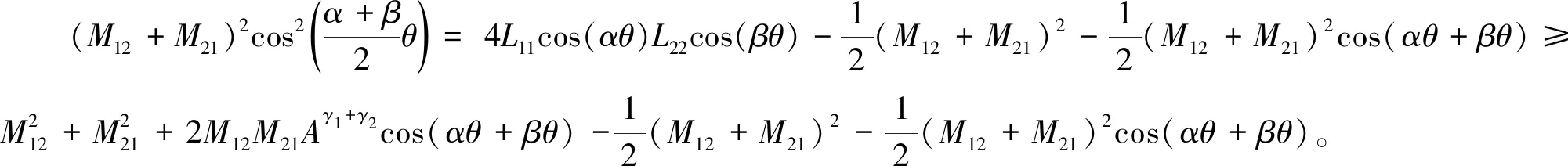
因此minG(θ)=G(0)=0，故Re(Zs)≥G(θ)≥0,θ∈[-π/2,π/2]。故可知串联得到的阻抗无源。

并联情况下，可知其导纳矩阵的实部为

(33)

对式(33)右端前两项使用重要不等式可得

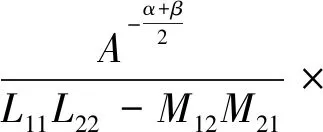
(34)

后续证明过程与阻抗证明过程相同，在此不再赘述。

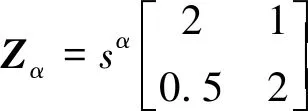
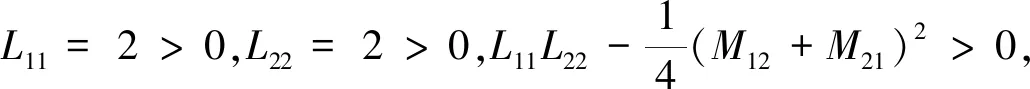
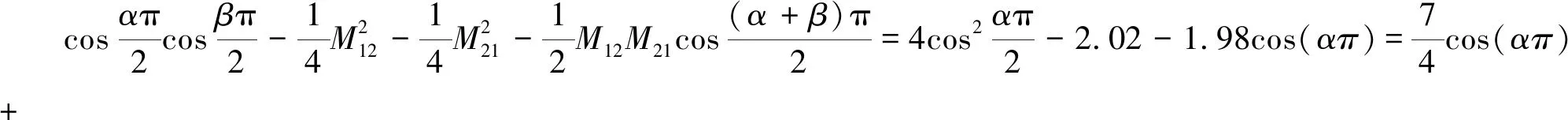
(35)

为了对本例进行直观说明，图4和图5中分别给出α=0.5和α=0.95时式(26)中F(θ)随θ变化的2D及随(σ,ω)变化的3D图。

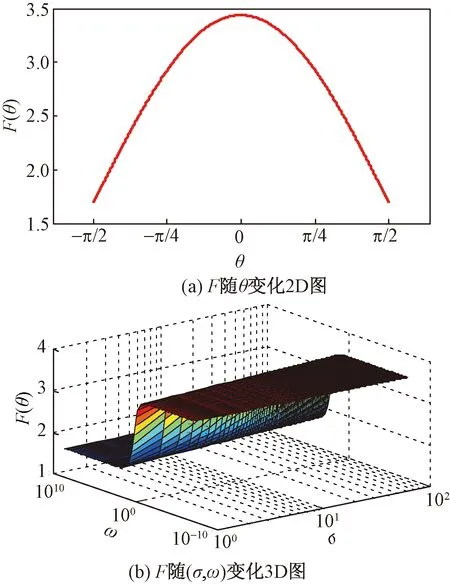
图4 α=0.5时F随参数变化情况Fig.4 Variations of F when α=0.5

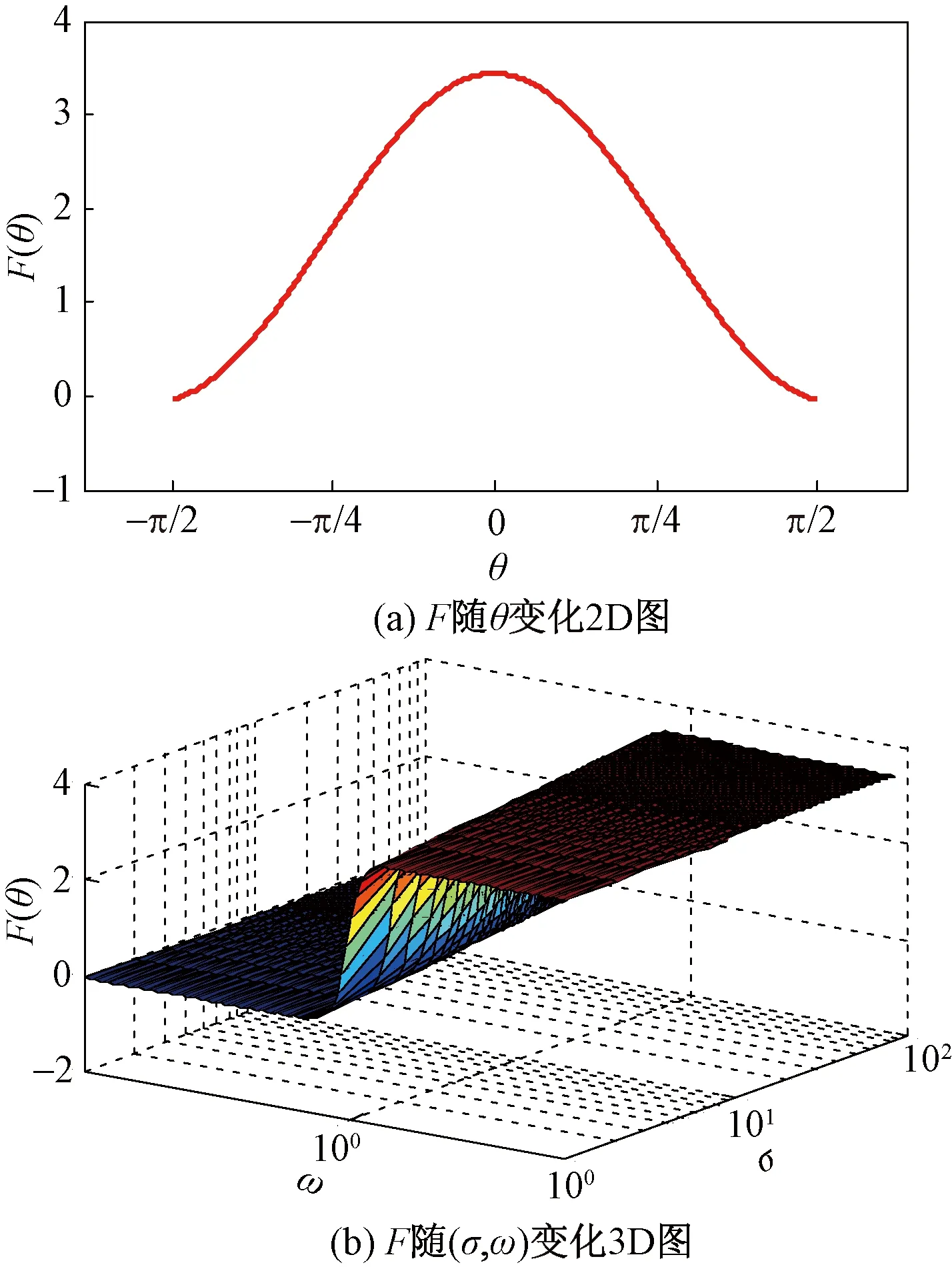
图5 α=0.95时F随参数变化情况Fig.5 Variations of F when α=0.5

由图4可知，在α=0.5时，F均为正值，其最大和最小值分别为3.437 5和1.687 5，此时元件无源；图5中，α=0.95时，F不能保证恒为正，其最大和最小值分别为3.437 5和-0.041 0，故这种情况下FMI元件有源。

现通过图6所示电路对α=0.95时该FMI有源性进行说明。

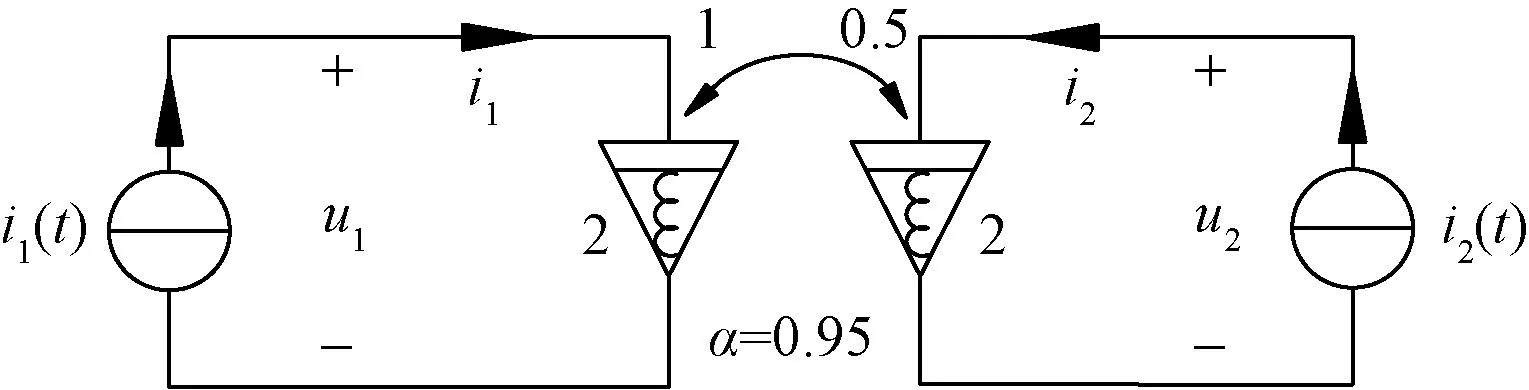
图6 例2验证电路Fig.6 Verification circuit for example 2

取i1(t)=sin(t-80°)，i2(t)=sin(t+60°)。正弦稳态下，由式(3)可以求得电压为：u1(t)=2sin(t+5.5°)+sin(t+145.5°)=1.391 3sin(t+33.015 7°);u2(t)=0.5sin(t+4.5°)+2sin(t+145.5°)=1.648 6sin(t+134.258 3°)。

可知该元件在α=0.95时，不断向外发出能量，故可知该元件有源。图7中给出了两个端口的电压、电流及瞬时功率；图7(c)中总瞬时功率的最大值和最小值分别为：0.733 7和-0.830 4，该FMI在向外电路提供能量。

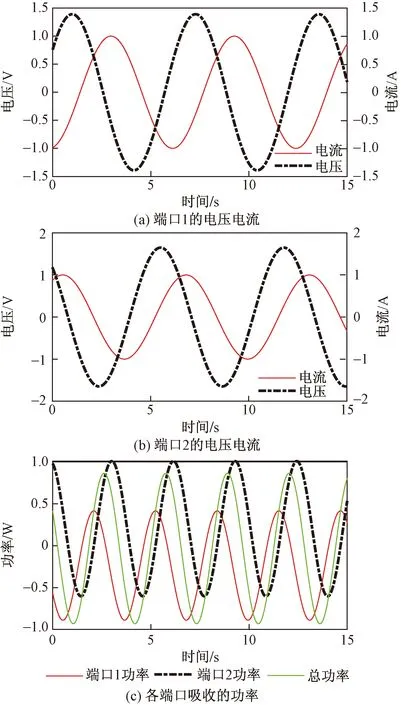
图7 验证电路正弦稳态下的电压电流及功率(例2)Fig.7 Voltages,currents and powers of circuit depicted under sinusoidal steady state(Case 2)

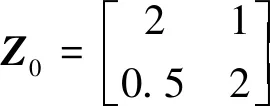
因为L11=1，L22=4，M12=-1，M21=3，α=0.7，β=0.9，γ=0.8满足式(10)～式(12)的条件，则可根据式(13)判定该元件的无源性。图8给出了F随θ变化的2D图及随(σ,ω)变化的3D图。由图8可以看到，F随θ变化过程中，最大值和最小值分别为：3和-3.429 4，因此该元件有源。

图8 例3中F随参数变化情况Fig.8 Variations of F in example 3

为了验证所得结论，现通过图9所示电路对其进行说明。取端口电流为：i1(t)=sin(t-63°)，i2(t)=sin(t+150°)，正弦稳态下由式(3)可以求得端口电压分别为：u1(t)=sint-sin(t+222°)=1.867 1sin(t+20.996°)；

u2(t)=3sin(t+9°)+4sin(t+231°)=2.616 7sin(t-80.413 0°)。

图10中给出了端口电压、电流及瞬时功率；图10(c)所示总瞬时功率的最大值和最小值分别为：0.561 7和-2.033 9，可以看到该FMI在向外界提供能量，故知该元件有源。

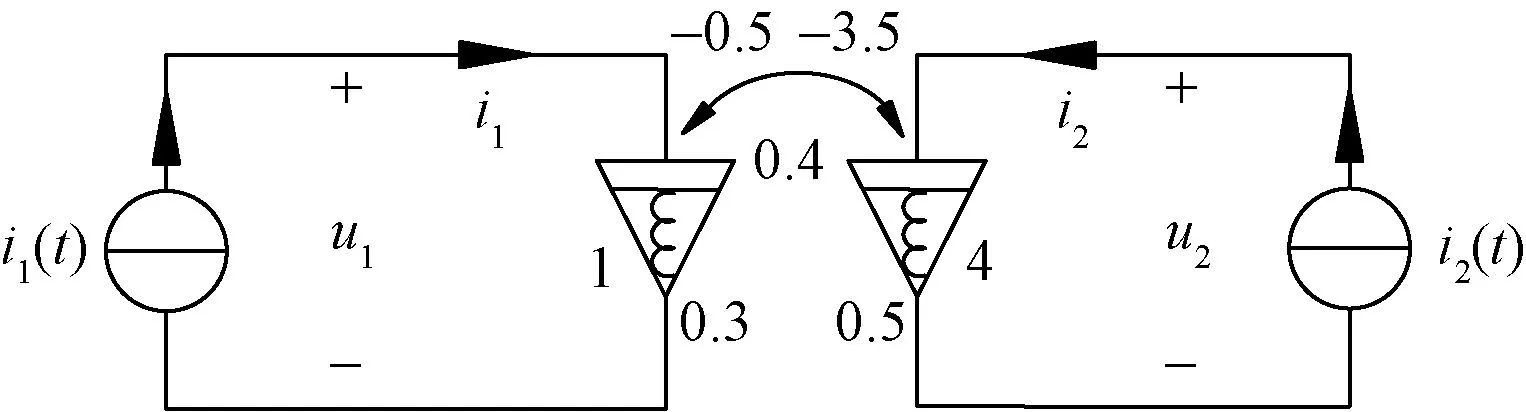
图9 例3验证电路Fig.9 Verification circuit for example 3

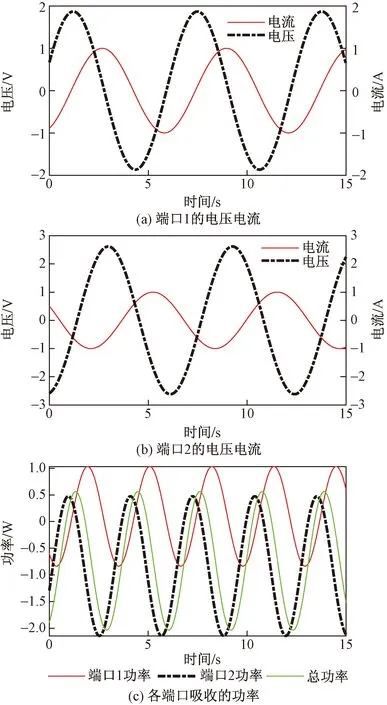
图10 验证电路正弦稳态下的电压电流及功率(例3)Fig.10 Voltages,currents and powers of circuit depicted under sinusoidal steady state(Case 3)

由例1～例3可知，FMI的无源性除了与参数矩阵相关外，分数阶次的影响也非常大。FMI的无源性结论与传统整数阶耦合电感的无源性结论存在差异：①无源整数阶耦合电感一定是互易的，而无源FMI可以是非互易的；②电感矩阵相同的同元次FMI的无源性与分数阶阶次密切相关；③非同元次FMI的无源性与参数矩阵和阶次均密切相关。

4 结论

FMI的提出进一步丰富和完善了电路元件体系，研究其无源性对分数阶电路的分析与综合具有重要意义。从频域入手，基于广义坐标和耗散矩阵的概念，推导获得了FMI的无源条件。该条件不仅与元件的伪自感和伪互感相关，而且与阶次关系密切。可以看到，FMI的无源性结论与传统耦合电感的无源性结论存在较大差异，无源FMI可以是互易的，也可以是非互易的。已有的整数阶耦合电感仅为FMI中极为特殊的一类。讨论FMI的无源性将为分数阶电路的分析与综合奠定重要理论基础。未来的研究方向将包括分数阶网络的无源性判据及相关的电路综合方法研究。