基于改进自适应粒子群算法的混合核函数最小二乘支持向量机大坝变形预测

2021-02-24梁耀东栾元重刘方雨纪赵磊

科学技术与工程 2021年1期

梁耀东,栾元重,刘方雨,纪赵磊,庄艳

(山东科技大学测绘科学与工程学院，青岛 266000)

建立合理精准的分析预测模型是大坝安全监测中的一项重要工作[1]。大坝变形监测时间序列是多种内力的宏观表现，期望能从含有内部力学演化的已知观测数据中，找到演化的规律以及能够预测未来的发展动态，进而反馈给安全管理部门，可以及时采取相应的处理措施[2-4]。

近年来，神经网络、支持向量机(support vector machine，SVM)和最小二乘支持向量机(least squares support vector machines,LSSVM)等算法开始应用于坝体变形时间序列的模拟预测分析。李松等[5]研究表明神经网络是基于大样本的一种学习方法，当样本量较少时会造成预测误差过大，同时该方法容易出现过学习现象。SVM模型可以较好地解决局部最优、非线性、小样本训练等问题，LSSVM模型将不等式约束替代等式约束，通过求解最小二乘线性方程组得到决策函数，更加便于求解，也避免了SVM的二次规划问题[6-8]。核函数的选择对模型的特性有决定性影响，为了提高模型的精度，提出一种由全局多项式核和局部高斯核线性组成的混合核函数。由于LSSVM模型的参数严重影响预测结果，而粒子群算法(particle swarm optimization，PSO)有简单、收敛速度快和全局寻优的特点，现采用一种加入变异因子的自适应PSO算法对非线性LSSVM模型参数寻优，并将之应用于水坝变形分析与预测，以验证混合核函数PSO-LSSVM模型在水坝变形预测中的应用效果。

1 基本原理

1.1 最小二乘支持向量机

SVM的基本思想是通过内积函数定义的非线性变换将输入空间变换到一个高维空间，在这个高维空间中寻找输入变量和输出变量之间的一种非线性关系[9]。LSSVM是标准SVM的一种扩展，将不等式约束替代等式约束，把误差平方和损失函数作为训练集的经验损失，从而把问题转换成一个线性矩阵求解问题[10-12]。

假如有一组样本数据集{(xi,yi)|xi∈Rm,i=1,2,…,n}，其中xi为输入向量，yi为输出值，n为样本总数。通过非线性函数φ(x)将输入空间映射到高维特征空间[13]，可得回归估计函数为

f(x)=wTφ(x)+b

(1)

式(1)中：w为超平面n维权值向量；b为偏置量。

LSSVM定义优化问题的目标函数为

(2)

式(2)中：c为惩罚系数；ei为松弛变量。

约束条件为

yi[wTφ(x)+b]=1-ei

(3)

将式(3)代入Lagrange函数可得

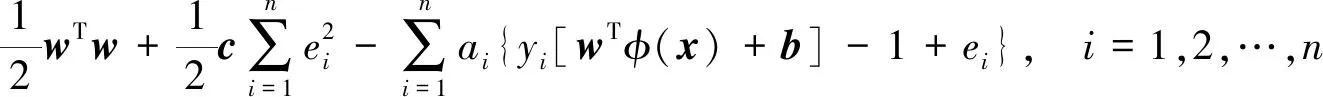
(4)

式(4)中：ai为拉格朗日乘子，且ai≥0。

由KKT(Karush-Kuhn-Tucker)优化条件可得

(5)

式(5)中：e=(1,1,…,1)T；α=(a1,a2,…,an)T；Y=(y1,y2,…,yn)T；K为核函数矩阵。

传统的核函数包括线性核函数、多形式核函数、高斯径向核函数(radial basis function，RBF)、拉普拉斯核函数等函数，Smits等[14]提出了一种混合核函数，即将两个不同的核函数组合起来，使得混合后的核函数性能更佳。核函数组合的方法很多，但最终的混合核函数要满足 Mercer 条件。通过组合两种具有代表性的高斯径向核函数和多项式核函数的映射特性，构造一种混合核函数，此混合核函数满足Mercer 条件[14]。该混合核函数拥有高斯径向核函数的局部特性(函数的学习能力强)，也可拥有多项式核函数的全局特性(泛化能力强)，且多项式核函数选择二阶。传统的多项式核函数、高斯径向核函数和混合核函数表达式分别为

K(x,xi)=(xTxi+1)q

(6)

(7)

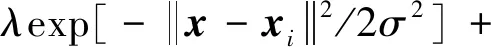
(1-λ)(xTxi+1)q

(8)

式中：σ为RBF核函数宽度；q为多项式核函数系数；λ为混合权重系数。

最终得到LSSVM的回归函数模型为

(9)

根据回归理论可知,它的主要参数是RBF核函数参数σ、多项式核函数系数q、惩罚参数c和混合权重系数λ,这4个参数对模型的学习和泛化能力影响很大，现采用改进的自适应粒子群算法来优化选择4个参数σ、q、c和λ，在一定程度上减少了主观经验选择的盲目性。

1.2 改进的自适应粒子群算法

粒子群算法是模拟鸟群觅食行为，其原理是粒子从随机解出发迭代寻找最优解，并通过追随当前搜索到的最优值来寻找全局最优[15-17]。假设在N维空间m个粒子组成的一个群体，粒子的位置由{xi=(xi1,xi2,…,xiN),i=1,2,…,m}来表示，粒子对应的飞行速度由[vi=(vi1,vi2,…,viN),i=1,2,…,m]来表示，通过根据各粒子的适应度值来评价其优劣性，并迭代找到每个粒子的当前最优位置即个体最优值Pbest=(pi1,pi2,…,piN)和所有粒子的当前最优位置即局部最优值Gbest=(g1,g2,…,gN)，粒子群的速度、位置更新公式分别为

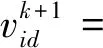
(10)

(11)

图1 改进自适应混合核函数PSO-LSSVM算法流程图Fig.1 Improved adaptive hybrid kernel function PSO-LSSVM algorithm flow chart

在PSO搜索中，惯性权重系数w的选择十分重要，线性递减权重并不适合优化搜索过程，改用非线性权重递减可以提高预测精度，w的表达式为

(12)

(13)

式中:yi为第i个样本的实测值；Yi为第i个样本的预测值；f(xi)为粒子当前的适应度值；favg和fmin分别为当前粒子中的平均和最小适应度值，通过粒子的离散程度来动态调节粒子的惯性权重。

2 改进自适应PSO-LSSVM模型的建立

采用改进的自适应PSO算法对LSSVM模型中的两个参数(RBF核函数参数σ、多项式核函数系数q、惩罚系数c和混合权重系数λ)进行优化寻优，其具体实施步骤如下：

(1)输入训练样本数据和预测样本数据，并对数据进行归一化处理，并对粒子的速度和位置进行初始化处理。

(2)对参数进行设置，粒子群规模m=20；迭代次数取kmax=100,对于加速度常数，c1值较小会导致粒子缺失认知能力，c2值较小会降低粒子间的信息共享能力，其取值范围通常为0～2。根据经验一般都取2，本文取c1=1.5，c2=1.8；对于惯性权重系数w，初始化w0=1.0，设置变化范围为0.3～0.9；RBF核函数参数σ∈[0.01,100]，多项式核函数参数q∈[0.1,4]，惩罚系数c∈[0.01,2 000],混合权重系数λ∈[0,1]。

(3)建立PSO-LSSVM模型，由式(10)、式(11)更新粒子的速度和位置，根据式(13)计算粒子的适应度值f(xi)，并与所有粒子的最优适应度值f(Gbest)进行比较，选取最小的f(xi)值，并代替f(Gbest)，由式(12)计算、更新惯性权重系数w，最终终止条件为kmax=100或者满足f(xi)≤0.001，最后寻找出全局最优参数，并建立改进自适应混合核函数PSO-LSSVM模型。

模型确定后算法程序实现如图1所示。

3 工程应用

丰满大坝为混凝土重力坝，长1 080 m，高91.7 m，实验数据为丰满大坝30#坝段监测成果[18]，包括水平变形、同期观测水位值、温度，将同期观测水位值和温度作为属性特征。选取1985年4月20日—1987年10月25日的140组数据作为原始数据，其中选取前125组数据作为训练样本数据，后15组数据作为预测数据。

3.1 模型训练结果与分析

利用MATLAB 2014b软件上的LSSVM工具箱，编码实现了改进的自适应粒子群算法分别对混合核函数的最小二乘支持向量机、多项式核函数最小二乘支持向量机和RBF核函数最小二乘支持向量机进行参数寻优，寻优结果如表1所示，拟合结果如图2所示，3种不同核函数的拟合误差结果如图3所示。

图2 不同核函数PSO-LSSVM结果与原始数据对比Fig.2 Comparison of PSO-LSSVM results with different kernel functions and original data

表1 不同核函数PSO-LSSVM模型的参数寻优结果Table 1 Parameter optimization results of different kernel function PSO-LSSVM models

由图2可知，混合核函数PSO-LSSVM模型的拟合度最高，多项式核函数PSO-LSSVM次之，RBF核函数PSO-LSSVM则最差。根据不同核函数模型的拟合值与真实值的对比分析可得：RBF核函数PSO-LSSVM模型的拟合曲线的均方根误差为0.42 mm，多项式核函数PSO-LSSVM模型的拟合曲线均方根误差为0.3 mm，混合核函数PSO-LSSVM模型的拟合曲线均方根误差为0.26 mm，因此混合核函数的PSO-LSSVM模型和传统的单个核函数PSO-LSSVM模型拟合精度高，另外从图2中可以看出，混合核函数在曲线波动较大处或拐点处，依然有很好的拟合值。

图3为3种不同核函数模型对坝体的水平位移的拟合误差对比，从图3中可以发现RBF核函数PSO-LSSVM拟合误差波动比较大，相对比较离散，误差范围主要在[-1.2,1]；多项式核函数PSO-LSSVM模型的拟合误差值相对于前者更加向0轴附近靠拢；而较之前两者，混合核函数PSO-LSSVM模型的拟合误差值就更加稳定且更小，其误差值在[-0.4,0.3]范围内。

图3 不同核函数模型拟合误差对比Fig.3 Comparison of fitting errors of different kernel function models

3.2 模型预测结果与分析

表2给出了RBF核函数PSO-LSSVM模型、多项式核函数PSO-LSSVM模型和混合核函数PSO-LSSVM模型的预测值，以及对应的相对误差和中误差。由表2可知，RBF核函数PSO-LSSVM模型的预测相对误差绝对值范围为1.8%～20.3%，其中误差为0.23 mm；多项式核函数PSO-LSSVM模型的预测相对误差绝对值范围为0.7%～16.8%，其平均值为6.7%，中误差为0.21 mm；混合核函数PSO-LSSVM模型的预测相对误差绝对值范围为0.3%～10.8%，其平均值为5.2%，中误差为0.16 mm，对比前两种模型，可以看出其预测精度提高了。发现在具有良好发展趋势的情况下，预测精度较高，而在曲线波动较大处或拐点处，传统的单核函数模型的预测精度都相对降低了，比如预测序号11处，说明时间序列趋势性是否良好将影响预测精度，对于这种情况，混合核函数模型发挥了两种核函数的兼容性，能够很好地提高预测精度。