离散单元法分析隔振沟引起的强夯变形和应力变化
2021-02-24李玉岐杨赋安张文杰
李玉岐, 杨赋安, 张文杰
(上海大学土木工程系, 上海 200444)
强夯法作为一种地基加固方法, 是通过重锤所具有的夯击能在极短的时间内对地基土体施加一个巨大的冲击能量, 使一定范围内的土体孔隙挤密、地基强度增加, 从而达到地基加固的目的.由于具有施工工艺简单、加固效果明显、适用范围广等优点, 强夯法得到了广泛的应用.然而, 强夯法施工会产生巨大的冲击能量及强烈的地表振动, 对周围环境造成很大的影响.方磊等[1]通过现场检测得到了不同夯击能下强夯地基处理施工时所产生的地面振动, 认为强夯引起的地面振动加速度衰减到0.1g(g 为重力加速度)时, 对建筑物几乎没有危害;李福民等[2]通过分析地表振动加速度的传播规律, 研究了隔振沟的隔振效果及其对振动传播规律的影响, 得到了强夯加固地基安全距离的估算方法;杨龙才等[3]通过考察瑞利波的径向振动量和竖向振动量沿地基深度的衰减特性, 认为竖向振动量是引发环境安全的主要因素;李润等[4]通过分析强夯振动加速度、速度随测点距离的衰减关系, 评价了隔振沟的作用;李盼盼等[5]通过现场试验记录了强夯振动加速度在平面和斜坡的传播和衰减过程, 探讨了强夯振动波延水平面和斜坡的传播规律以及能级对振动加速度的影响;周洋等[6]探讨了振动加速度与强夯能量、传播距离之间的关系, 建立了2 种能级振动加速度衰减公式, 提出了建筑物最小安全距离的确定方法及减轻强夯振动影响的工程措施.国外很多学者也进行了相关研究, Andersen等[7]通过建立的二维数值模型研究了3 种隔振措施的隔振效果, Chiang 等[8]采用二维边界元方法、Jiang 等[9]采用有限元-边界元相结合的方法分析了不同参数对隔振沟隔振效果的影响.
综上可以看出, 前人研究都是从宏观角度进行考虑, 且大多是从隔振沟对振动加速度的影响方面分析隔振效果, 较少从隔振沟对地表变形和应力变化影响的角度分析隔振效果.本工作以强夯法加固地基为切入点, 基于离散元理论建立数值模型, 从微观尺度分析不同隔振沟深度和位置对冲击荷载引起的地表隆起变形的影响, 探讨隔振沟对地基应力传递的影响, 以期丰富强夯法地基处理的理论, 指导强夯法地基处理的设计, 并为其他冲击荷载的隔振设计提供借鉴意义.
1 模 型
1.1 本构模型
选取颗粒流程序PFC(Particle Flow Code)[10]自带的一种特殊本构模型——滞回阻尼接触模型模拟土体在强夯施工过程中的动力特性, 其本构关系如图1 所示.由图1 可知, 模型的法向刚度在加载和卸载阶段并不相同, 且卸载刚度远大于加载刚度.

图1 滞回模型本构关系Fig.1 Constitutive relation of hysteresis model
因为本工作中的干砂土体不考虑颗粒之间的抗拉强度, 所以动力滞回圈只在接触力的正向区域出现, 这一特性很好地反映了土体在冲击荷载作用下的刚度变化.加卸载刚度为

式中:Rh为滞回阻尼系数, 取0.75;k0为颗粒加载刚度和卸载刚度的平均值, 取静力作用下颗粒的初始法向刚度, 由数值双轴试验确定.
1.2 模型的建立及参数确定
本工作模拟Takada 等[11]进行的强夯离心机试验, 有关装置和参数参考文献[11-12].考虑离心机模型试验的对称性, 建立二维轴对称模型, 编写程序, 生成符合离心机试验所选土样颗粒级配的数值模型.首先, 将级配曲线分段, 得到分段点的粒径及对应的质量分数, 两个分段点对应的质量分数差即为粒径区间段土样占整个土样的质量分数;然后, 以排斥法随机生成每个区段所对应的土体颗粒;最后, 设置数值模型的离心加速度为50g, 与室内离心机试验的加速度一致, 运行程序, 颗粒相互排斥充斥整个空间形成土样模型.图2 为离心机试验土样的颗粒级配曲线.为了提高数值计算的运行效率, 剔除小于0.3 mm 粒径的颗粒后, 数值模型的颗粒级配曲线见图2(b).

图2 土样的颗粒级配曲线Fig.2 Particle grading curve of soil sample
本工作参考文献[12]中数值模拟的细观参数(见表1).另外, 轴对称模型的孔隙率为0.12,泊松比为0.3, 时间步长为1.0×10−6s, 数值模型的强夯能级与离心机试验的强夯能级一致, 均为4 380 kN·m.室内离心机模型试验的模型尺寸较小(高0.13 m, 半径0.15 m), 为了研究隔振沟对强夯冲击荷载的隔振作用, 本工作中的数值模型适当增加了离心机试验模型的水平方向尺寸(高0.13 m, 半径0.3 m).数值模型如图3 所示, 其中隔振沟中心距离夯坑中心(模型左边界)0.072 m, 隔振沟宽度为0.024 m、深度为0.04 m.

图3 数值模型Fig.3 Numerical model

表1 数值模型的细观参数[12]Table 1 Microscopic parameters of numerical model[12]
在PFC 数值模型中, 配位数、孔隙率、应力和应变率均是在一定测量范围内近似计算求得的, 该测量范围一般用测量圆来划分.为了研究夯锤冲击荷载作用下土体颗粒的接触应力变化, 在数值模型中设置75 个测量圆, 测量圆半径为0.006 m, 其具体布置方式和编号如图4 所示.建立其他隔振沟深度和位置的数值模型时, 采用上述模型的生成方法以及标定的细观参数, 只用进行隔振沟深度和位置的变化, 其他参数及测量圆布置方式均相同.

图4 测量圆布置图Fig.4 Distribution of measuring circles
2 结果及分析
考虑到分析问题直观方便, 下述的距离和变形都为真实的距离和变形, 即将模型尺寸和数值计算的结果乘以50(数值模型的离心机加速度为50g).
2.1 隔振沟深度对地表变形的影响
隔振沟设置于距离震源中心(位于模型左边界处的夯坑中心)3.6 m 处, 隔振沟宽度1.2 m,深度分别为1.0、2.0、3.2 和4.4 m.为了避免地表颗粒位移太大或飞出, 监测位移的颗粒位于地表下20 cm, 与震源中心水平距离分别为5、6、7、8、9、10、11、12、13 和14 m.
图5 为地表下20 cm 深度监测点的竖向位移时程曲线.由图5 可知, 随着时间增加, 各监测点的竖向变形增大, 在约0.4 s 时开始趋于稳定, 反映了强夯施工过程中强大的冲击力和侧向挤压引起周围土体隆起.未设置隔振沟时, 距离震源(夯坑中心)5 和10 m 处的监测点竖向变形较大, 而在距离震源中心7 和14 m 处监测点的竖向变形较小.这是由于在夯锤的冲击和侧向挤压作用下, 夯坑周围土体颗粒以水平运动为主, 且有向上运动的趋势, 造成夯坑周围土体发生隆起变形, 并在距离夯坑5 m 处达到最大值.这与贾敏才等[13]提出的土体动应力影响距离区间在2 倍左右锤径范围的结论相吻合.对于距离夯坑较远的地方, 地表的隆起则主要是由夯击锤体斜下方土体颗粒表现的竖向冲击压密与水平挤密作用相结合引起深部土体发生侧向位移引起的.由于隔振沟的隔断作用, 距离震源5 m 处, 土体受到的水平挤压作用明显减弱,该处的最大隆起量大大减小.同时, 由于隔振沟本身的变形, 使得深层土体的侧向挤压作用减小, 因而距离震源10 m 处的地表的最大隆起量也大大减小.
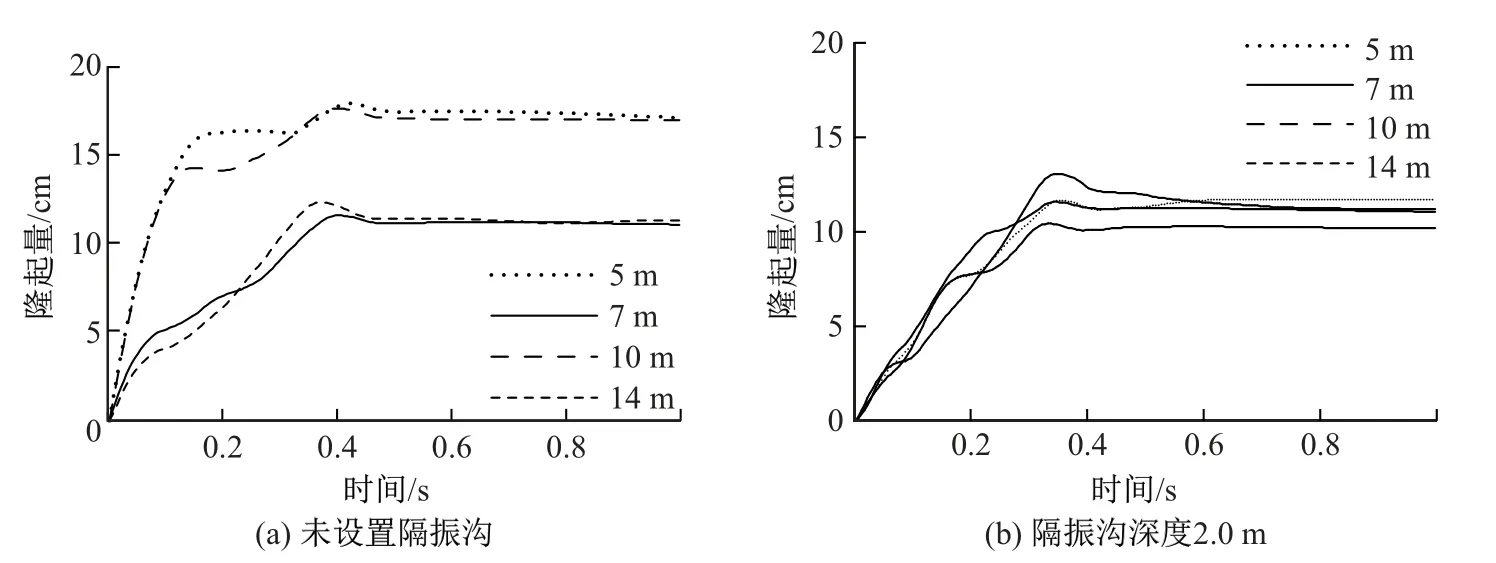
图5 地表不同测点的竖向位移时程图Fig.5 Vertical displacement diagram of different measuring points at the ground surface
图6 为隔振沟深度与地表隆起量的关系.由图6 可知: 在距夯坑中心5 和6 m 距离处, 设置不同深度的隔振沟都能较好地抑制土颗粒的运动, 使得地表的隆起变形量较无隔振沟时大大减小;在距夯坑中心7 m 处, 由于该点位于夯击水平挤压引起的隆起变形与深部土体的侧向挤压引起的隆起变形分界处, 地表隆起变形较小;对于距夯坑中心距离大于7 m 的区域, 隔振沟的设置对于地表的隆起变形同样具有很好的抑制作用.因此, 设置隔振沟可以大大减小地表的差异沉降量, 有效避免因差异沉降引起的地面开裂.随着隔振沟深度的增加, 地表竖向位移基本呈递减的趋势[14], 但变化并不是很大.综合考虑隔振沟的施工成本和对地表隆起的抑制效果, 设置隔振沟深度为2.0 m 比较合适.

图6 地表隆起与隔振沟深度的关系Fig.6 Relationship of maximum vertical displacement and depth of isolation trench
2.2 隔振沟位置对地表变形的影响
为了优选隔振沟的位置, 对比分析隔振沟位置对地表隆起的影响, 其中隔振沟深度为2.0 m, 隔振沟中心与震源的距离分别为3.6、4.2、4.8、5.4 和6.0 m, 隔振沟宽度均为1.2 m.图7 为地表隆起与隔振沟位置的关系, 其中由于研究隔振沟与震源之间地表隆起值的工程意义不大, 故未绘制这些范围的地表隆起值.由图7 可知, 距离震源不同位置的隔振沟, 都对地表隆起变形起很大的抑制作用, 尤其对于未设置隔振沟时距离震源5 和11 m 的地表隆起, 抑制作用更加明显.地表隆起变形受隔振沟位置的影响较小, 说明隔振沟对抑制地表隆起变形作用明显, 但受隔振沟位置影响不大.因为当隔振沟位于夯点之外3.6 m 时的地表隆起变形较小, 所以隔振沟布置在夯点之外3.6 m 处比较合适.

图7 地表隆起与隔振沟位置的关系Fig.7 Relationship of maximum vertical displacement and location of isolation trench
2.3 隔振沟对应力的影响
为了进一步说明隔振沟的作用, 对比分析隔振沟对颗粒接触应力的影响, 本工作选取隔振沟右侧(远离夯坑的一侧)3 m 范围内的测量圆(27∼31、38∼42、49∼53、60∼64、71∼75 号)进行分析.
图8 和图9 分别是由71-75 号测量圆测得的水平应力和竖向应力时程曲线.由图8 和图9可知: 未设置隔振沟时, 初始的水平应力和竖向应力均较大(120 kPa), 但随着时间的变化迅速减小, 在0.45 s 左右趋于稳定;当设置隔振沟时, 初始的水平应力和竖向应力则相对较小(小于40 kPa), 从衰减开始到趋于稳定约为0.45 s.因此, 设置隔振沟可以显著减小隔振沟外土体的初始应力水平.从图8 和图9 还可以看出, 水平应力和竖向应力有多个峰值, 这是由于当距离夯坑达到一定范围时, 在夯锤竖直线周围小于60◦的范围以外是以瑞利波为主, 土体动应力会出现第二峰值[15].

图9 竖向应力时程曲线Fig.9 Vertical stress curves versus contact time
为研究不同深度处的应力受隔振沟深度变化的影响, 本工作以设置在距离震源3.6 m 的隔振沟为例, 此时监测点与震源中心水平距离5.1 m.选取72 号(0.3 m 深度)、61 号(1.7 m 深度)、50 号(2.9 m 深度)、39 号(4.1 m 深度)、28 号测量圆(5.3 m 深度)的初始应力与衰减后稳定的应力之差进行对比分析, 结果如图10 所示.由图10 可知: 隔振沟深度对土体的水平应力和竖向应力变化影响较小, 但基本都小于未设置隔振沟的应力衰减值;监测点的应力衰减值随着深度的增加先增大后减小, 并且在距离地表2.9 m 深度时达到峰值;随着监测点深度的增加,设置隔振沟的应力衰减差值与未设置隔振沟时的差值逐渐靠近, 说明隔振沟对应力的影响随深度的增加逐渐减小;当深度大于4.0 m 时, 隔振沟的设置对远离震源一侧监测点处的应力影响甚微, 这说明隔振沟的隔振效果在达到临界沟深以后不再随沟深的增加而显著提高[16].因此, 隔振沟的隔振作用主要是削弱强夯施工过程中的应力传播路径, 并且隔振沟对土体应力的影响具有一个影响深度, 当超过这个影响深度时, 隔振沟对土体应力传递的影响可以忽略不计.另外, 设置隔振沟应注意保护地下深处的管线和建筑物.

图10 应力变化与隔振沟深度的关系Fig.10 Relationship of the change of stress and the depth of isolation trench
3 结 论
本工作采用离散数值模拟方法研究了隔振沟深度和位置对场地周围地表变形以及土体应力变化的影响, 得到如下结论.
(1)未设置隔振沟时, 震源之外5 和11 m 处的地表隆起较大;设置隔振沟可以有效减小地表的隆起变形, 但隔振沟深度达到临界深度后, 隔振沟深度和位置对地表隆起变形的影响较小.综合考虑施工成本等因素, 认为隔振沟深度为2.0 m、隔振沟距震源3.6 m 比较合适.
(2)隔振沟是通过切断颗粒间的应力传播路径来减少对周围环境影响的.隔振沟的设置可以显著减小隔振沟外土体的初始应力水平, 并对隔振沟以下一定深度范围内的土体应力传递有较大影响, 但当超过隔振沟的影响深度后, 隔振沟对土体应力传递的影响可以忽略不计.在实际施工过程中, 针对较深处的地下建筑物和管线应另做专门的方案.
