耦合谐振子的量子绝热捷径设计
2021-02-24杨冠卓
杨冠卓, 陈 玺
(上海大学理学院, 上海 200444)
量子绝热定理是量子力学中的一个重要结论, 在量子绝热操控、量子绝热计算和量子绝热模拟方面具有重要的应用价值.量子绝热过程是指当外参量随着时间缓慢变化时, 量子态沿着其瞬时本征态演化[1].在实际过程中由于量子绝热的慢过程, 量子态的制备或操控往往会受到退相干的影响, 而失去保真度.为此, 人们提出了量子绝热捷径技术[2-4], 旨在加快量子绝热的慢过程, 从而减小退相干的影响.量子绝热捷径技术包括了许多不同的方案, 例如基于量子不变量的反控制法[4]、反向透热补偿法[5-6]、无跃迁量子驱动法[7-9]等.这些方法在冷原子或囚禁粒子中转移、冷却得到了实验验证.例如, Schaff等[10]利用量子绝热捷径技术实现了冷原子和玻色爱因斯坦凝聚态在囚禁势中的无摩擦快速冷却.清华大学An 等[11]利用反向透热补偿实现了相空间中囚禁例子的快速转移.Deng 等[12]和Diao 等[13]利用反控制方法实现了简并费米气体的量子绝热捷径, 并用于设计超绝热热机.目前, 量子绝热捷径技术作为量子调控的一个有效手段, 被广泛应用于原子、分子和光物理以及统计物理等领域[14-18].
量子绝热捷径技术是基于谐振势动力学及其量子不变量理论提出的[4], 该模型不仅可以等效描述光学囚禁势中的原子冷却, 还可描述机械谐振子冷却[4]、晶格中光学传播[19]、RC 电路(resistor-capacitance circuit)[20]等.然而, 在某些情况下, 耦合谐振子而非单个谐振子模型及其相干操控则显得尤为重要.例如, 耦合谐振子可以描述光力机械振子[21-22]、多个相互作用囚禁离子[23]、囚禁势中相互作用的冷原子气体[24]等.由于耦合谐振子的两个振子因耦合相互影响, 与单个谐振子相比更难操控.特别地, 在机械谐振子等实验中常规绝热调频方案往往会因两个谐振子的相互干扰而产生非绝热的激发, 很难实现精准操控和基态能级的冷却.
针对这些问题, 本工作将基于Lewis-Riesenfeld 量子不变量[25-26]推广研究耦合谐振子的量子绝热捷径设计.通过推导Ermakov 方程反设计耦合谐振子的频率, 从而实现量子态的快速精准制备或操控.
1 量子不变量理论
对于含时哈密顿量H(t)描述的系统, 波函数Ψ(t)满足含时薛定谔方程

如果可以构造一个厄米算符I, 使它满足

则称I为该体系的动力学不变量(Lewis-Riesenfeld 不变量).I的本征方程可以写为

式中:n=0,1,··· ,|φn(t)〉;λn为I(t)的本征值.薛定谔方程的解可表示为I(t)本征函数的线性叠加,
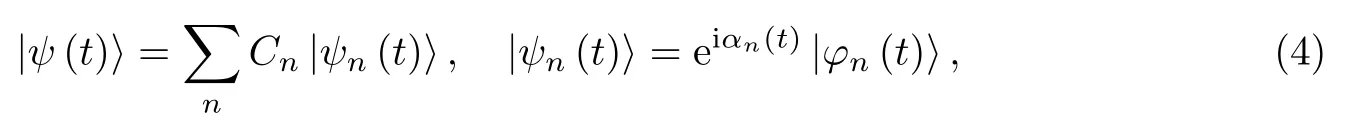
式中: 常数Cn满足归一化条件,Lewis-Riesenfeld 相位可以表示为

综上所述, 系统的演化算符可以表示为

根据H(t)=iħ可以得到

通常, 人们利用量子不变量来求解复杂的含时薛定谔方程, 而我们则根据系统量子态的演化,通过式(7)设计哈密顿量.接下来, 进一步展示如何利用量子不变量的动力学设计量子绝热捷径, 即先设计含时演化的路径, 从而反解哈密顿量的含时参量.一般来讲,I(t)和H(t)不一定对易.也就是说,I(t)的本征态所对应的态演化与H(t)的瞬时本征态不一致.为了达到量子绝热捷径的效果, 系统需要在初末时刻处于I(t)的本征态, 同时也处于H(t)的本征态[4,27].这要求I(t)和H(t)在初末时刻(t=0 和T=tf)具有同一组完备正交基矢, 即要求两者对易, 即有
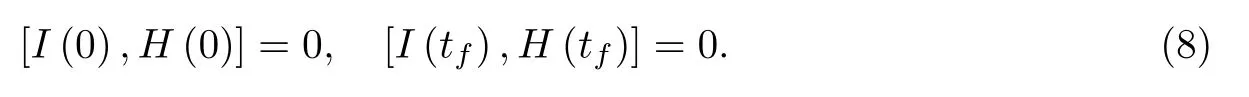
以式(8)作为边界条件设计出相关参数的演化路径, 可以取得量子绝热捷径的效果.接下来, 将以上述理论研究耦合谐振子的量子绝热捷径技术.
2 耦合谐振子模型
考虑一对耦合谐振子a 和b, 其哈密顿量可以表示为

式中:ma和mb分别为两个谐振子的质量;ωa(t)和ωb(t)分别为两个谐振子的含时频率;λ代表两个谐振子之间的耦合强度.式(9)中的位置算符和动量算符可以由产生算符ca()和湮灭算符cb()表示, 即其中,i=a,b.
于是, 体系的哈密顿量可以改写为

把这个哈密顿量对角化, 可以得到简正模式, 即


图1 为本征频率ωA、ωB随ωb/ωa的变化.单位频率为1 Hz, 耦合系数λ= 0.2.由图1 可以看出, 耦合谐振子的本征模式出现了类似冷原子二能级的能级反交叉.一般情况下, 人们只能通过缓慢绝热变化ωb/ωa, 才能进行量子态的操作.当绝热条件满足时, 系统的演化将始终保持在各自的模式上, 不出现非绝热跃迁.进一步分析可知, 2 个简正模式可以写成2 个新的简谐振子, 哈密顿量分别表示为

图1 耦合谐振子本征频率Fig.1 Eigenfrequencies of coupled oscillators

对于每一个简谐振子的哈密顿量, 都可以找到相应Lewis-Riesenfeld 不变量,


为后续设计方便,参照文献[4]中给出的方法,这里的ω0A(B)可以设置为初始简正频率ω0A(B)=ωA(B)(t=0).同样, 整个系统的第n能级的瞬时平均能量为

这样就可以通过量子绝热捷径技术设计此类耦合谐振子的频率, 实现上述末态基态能量(n=0)的减小, 从而实现快速无摩擦的冷却.
3 反设计方法
根据式(17), 两个简正模式的绝热捷径路径应满足式(8), 即有

式中:其中ωA(B)(t0)和ωA(B)(t0)为初末时刻的简正频率, 可以由初末时刻的裸频率ωa和ωb代入式(12)得到.为了设计量子绝热捷径, 可以选择满足这些边界条件的多项式作为拟设, 即有

式中:s=t/tf.把式(20)代入方程(17), 即可得到两个简正模式的绝热捷径演化路径.由此,根据式(12)进而可以得到裸频率ωa和ωb与简正频率ωA和ωB关系.
(1) 当ωa<ωb时,

(2) 当ωa>ωb时,


由此, 可以把从式(17)∼(20)得到的简正频率的绝热捷径路径代入式(22), 即可得到裸频率的绝热捷径路径, 实现耦合谐振子的绝热捷径路径设计.为了更好地理解上述设计量子绝热捷径的过程, 特此归纳为: ①由初末时刻的裸频率ωa(b)(t0)和ωa(b)(tf), 通过式(12)得到初末时刻的本征频率ωA(B)(t0)和ωA(B)(tf);②将满足边界条件(式(17))的标度参数bA(B)(t)代入式(19), 得到本征频率的绝热捷径演化路径ωA(B)(t);③将本征频率的绝热演化路径ωA(B)(t)代入式(22), 得到裸频率的绝热捷径演化路径ωa(b)(t).
图2(a)为量子绝热捷径设计的频率ωa(t)和ωb(t), 其中耦合系数为λ=0.1 和量子绝热时间为tf= 1 s.初始时刻ωa(0) = 1 Hz,ωb(0) = 10 Hz, 末时刻ωa(tf) = 1 Hz,ωb(tf) = 1 Hz,耦合系数为λ= 0.1, 量子绝热捷径演化时间为tf= 1 s, 绝热过程的演化时间为tf= 10 s.作为比较, 将整个演化时间变为tf= 10 s.此时, 整个演化过程转换为绝热调频, 如图2(b)所示.由图2(b)可知, 频率ωa不变化, 频率ωb则缓慢呈线性变化.这非常类似于二能级体系中的Landau-Zener 方案, 即Rabi 频率是常数, 失协量随时间线性缓慢变化.在上述两个例子中,选取初始时刻2 个振子的频率分别为ωa(0) = 1 Hz,ωb(0) = 10 Hz, 末时刻2 个振子的频率分别为ωa(tf)=1 Hz,ωb(tf)=1 Hz.

图2 两种调频方案的对比Fig.2 Comparision of two protocols
图3 为量子绝热捷径过程中的基态平均能量变化, 进一步表明可以利用量子绝热捷径技术调节频率ωa(t)和ωb(t), 实现耦合谐振子的基态(n=0)能量减小, 即耦合谐振子的冷却.此外, 绝热捷径的总演化时间tf越小, 中间激发能量就越大.这反映了能量和时间的测不准关系,即在物理上给出了量子绝热捷径的速度极限.

图3 量子绝热捷径过程中的基态平均能量Fig.3 Average energy of ground state in shortcut-adiabaticity modulation protocol
4 结束语
本工作基于量子不变量利用反控制法设计耦合谐振子的量子绝热捷径的演化方案.结果表明, 用量子绝热捷径技术调节耦合谐振子的频率时, 两个谐振子的频率需要变化.与绝热调频相比, 本方案中频率变化速度更快, 变化幅度更为剧烈, 但是整体的演化时间缩短, 并取得与原来绝热调频相同的结果.因此, 根据耦合谐振子量子基态的量子绝热捷径操控, 可以同时快速调节耦合谐振子的频率并且保证最终无非绝热的跃迁.从而避免了因两个振子耦合产生的相互影响导致的误差以及由此产生的非绝热跃迁.如前所述, 耦合谐振子广泛存在于机械谐振子等不同的物理模型中, 因此上述结果可以应用于量子热机中, 从而取代热机循环过程中的绝热冲程, 以期改善量子热机的热力学性能.此外, 这些结果还可以推广至3 个或多个耦合谐振子, 并实现量子纠缠态的超快操控.
