声脉冲传播法测定纤维动态弹性模量方法实证与标准化

徐星颖，刘方义，李红杰，李德利，刘洪涛

1.武汉纺织大学省部共建纺织新材料与先进加工技术国家重点试验室，武汉 430200；2.武汉纺织大学材料科学与工程学院，武汉 430200；3.上海市纺织工业技术监督所，上海 200082；4.中国化学纤维工业协会，北京 100020

0 引言

弹性模量是材料在弹性变形阶段应力和应变的比值以表征其刚性，也是纺织纤维的基本物理量之一。通常采用准静态拉伸法获得应力—应变曲线[1]，弹性变形区域直线段的斜率即为弹性模量的几何意义，其物理意义是产生100%弹性变形所需的应力。此法因具备同时计算拉伸强度、断裂伸长率、定伸应力、断裂功等系列参数的强大功能而被广泛采用，但拉伸时常伴弛豫，单调持续重载应力不能反映实际受力状态和材料结构变化，且破坏试样而不可重复。

基于声波高频交变轻载扰动致使纤维微小变形的声脉冲传播法测定动态弹性模量（声模量），构成了从另一角度接近实际应力和应变状态的重要方面。该方法通过测量波长远大于直径的声波在纤维中的纵向传播速度，巧妙利用纤维材料低维轻质特征，合理避开密度环节，仅用线密度即可精准表达弹性模量，并与分子取向结构参数相关联，无需分析拉伸曲线，可实现试样无损、重复利用，且操作简便、快捷、可靠，不仅适用于传统化纤生产过程的例行监测，还可用于芳纶[1]、超高分子质量聚乙烯纤维[2]、碳纤维[3]等国防高性能纤维及其前驱体，聚乳酸[4]、聚己内酯[5]等医用生物纤维的研发应用，但迄今未形成标准化操作方法。

1 试验

1.1 方法原理

根据声学理论，通过测定声波在纤维中的纵向传播速度C，结合纤维密度ρ即可计算其模量E=ρC2（E—Pa；ρ—kg/m3；C—m/s）。如图1，纤维试样左端固定，右端陆续经过脉冲声波发送换能器0、接收换能器L1（或L2），再由转向滑轮和施加预张力的夹式砝码垂向地面，试样平直但未被拉伸。

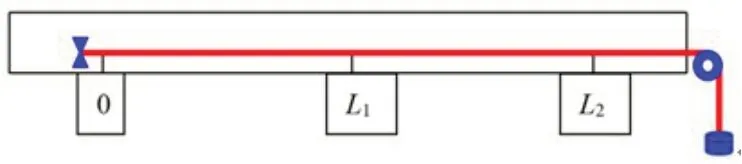
图1 声速法纤维弹性模量测定仪

当发送换能器与接收换能器分别在0 和L1处时，测得声波旅行时间TL1（travel time，见ASTM F89-68: Method for determination of the modulus of a flexible barrier material by sonic method）；当发送换能器与接收换能器分别在0和L2处时，测得声波旅行时间TL2；当发送换能器与接收换能器分别在0和Li处时（i=1,2,3,......,n），测得声波旅行时间TLi。TLi可由仪器直接读取，它包含声波在纤维中的传播时间Ttran和仪器系统的延迟时间T0（零距离传播时间），Ttran和T0都不能由仪器直接读取，但两者之和等于TLi，且一般认为T0是仪器系统所固有而恒定不变[6-7]，由电声、声电转换和节点传输所致。

可用多点外推法和两点倍长法计算延迟时间T0和声速C。由于存在延迟时间，不可采用单点数据进行计算。外推法是根据Li和TLi散点数据（Li,TLi）进行拟合直线作图，当以Li为x轴、以TLi为y轴时，拟合直线外推在y轴上的截距即为延迟时间T0；当以TLi为x轴、以Li为y轴时，拟合直线的斜率即为声速C。倍长法计算过程为：当L2=2L1时，C=L1/（TLi-T0）=L2/（TL2-T0）=2L1/（TL2-T0），故T0=2TL1-TL2。由此可进一步计算C。

任意两点法声速计算公式C=（Lm-Ln）/（TLm-TLn）。

冗长繁复的多点外推法通常更具统计意义且更为准确，而简便易操作的倍长法则受试样预张力和换能器隔距影响较大。本文旨在验证和优选两点倍长法参数设置以更接近多点外推法结果。

由于纺织纤维线密度X的定义隐含密度ρ和直径d，三者之间的关系为：X=250 πρd2（X—tex；ρ—g/cm3；d—mm）。上述模量计算式E=ρC2可变换为与ρ无关的公式，即：E=11.3C2（E—gf/den；C—km/s）或E=C2（E—N/tex，C—km/s）。

考虑到常用模量单位还有MPa、GPa，在此列出换算式，即：1 cN/dtex=1.13 gf/den；δ=100ρT（δ—MPa；ρ—g/cm3；T—cN/dtex）。

此外，如纤维无规取向的声速值Cu已知，则可进一步根据赫尔曼公式和莫斯莱公式计算无因次的取向度F和取向角θ：

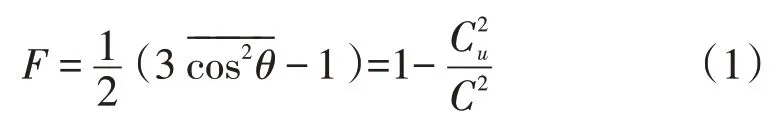
1.2 试验部分

直径为0.2 mm 的涤纶单丝为南通新帝克单丝科技股份有限公司产品，线密度44 tex，密度1.4 g/cm3，无规取向声速值Cu为1.35 km/s[8]。

从丝筒随机取长7 cm 单丝试样，按GB/T 6529—2008《纺织品 调湿及试验用标准大气》进行调湿处理。采用上海东华凯利新材料科技有限公司的SCY-IV型纤维取向度测量仪在室温环境下操作，脉冲声波频率为5 kHz，预载荷分别为10、20、30、40、50、60、70、80 g，对应预 张 力 分别为0.022、0.045、0.067、0.089、0.111、0.134、0.156、0.178 cN/dtex。换能器隔距组（L1,L2）分别为（50,100）、（50,150）、（50,200）、......、（50,450）；（100,150）、（100,200）、（100,250）、.......、（100,450）；.......；（400,450），共36 组，即在50～450 mm，每50 mm 及其整数倍的9 种隔距Li均测量8 次，读取（共计36 组72 个）声波旅行时间TLi数据，并计算在不同预张力作用下每种隔距的声波旅行时间平均值。

2 结果与讨论

2.1 多点外推法结果计算

表1 列出了不同预张力作用下涤纶单丝中声波旅行9种距离的平均时间。根据表1所列（Li,TLi）散点数据，以Li为x轴、以TLi为y轴，采用最小二乘法拟合直线外推在y轴上的截距即为延迟时间T0；以TLi为x轴、以Li为y轴时，拟合直线的斜率即为声速C。不同预张力下不同测量距离（换能器隔距）的延迟时间T0和声速C，汇总见表2带*两列。

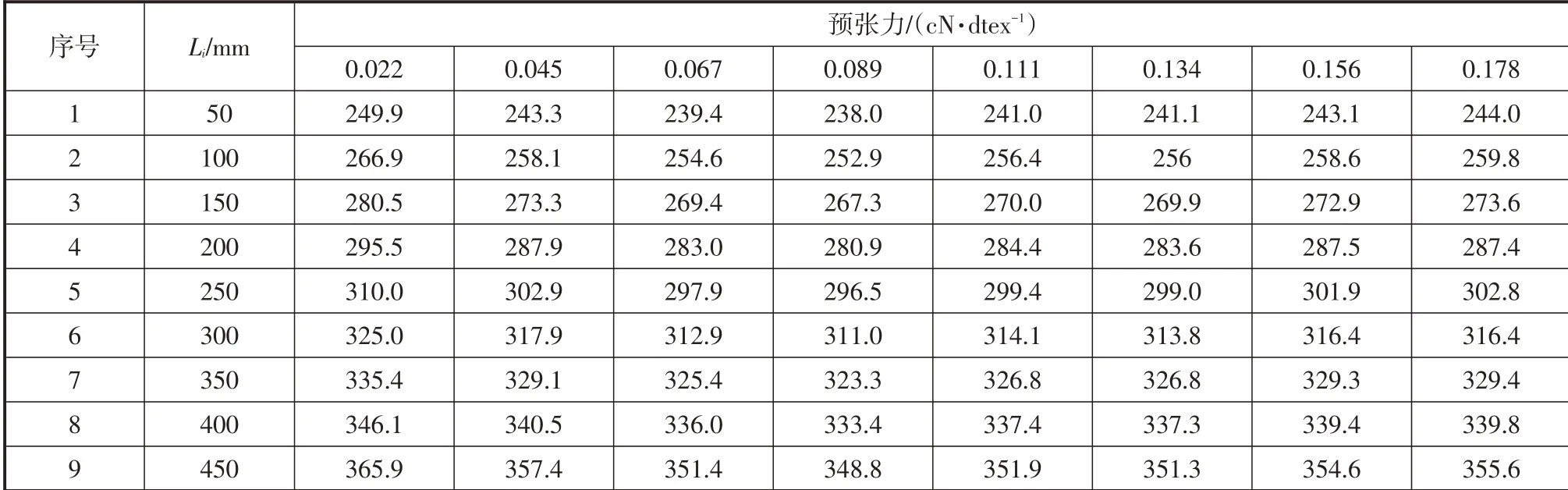
表1 在不同预张力作用下的涤纶单丝中声波旅行9种距离Li的平均时间TLi μs

根据声速C可计算声模量E，再结合Cu=1.35 km/s[8]，由公式（1）进一步计算取向度F和取向角θ，结果详见表3 和表4 带*两列。本文重点瞄准模量值E，测得值为17.5～18.3 GPa，略高于应力—应变法测得值12～18 GPa[9]，符合动态法模量测定值通常高于准静态法测定值这种一般规律[1-2]。如表5所示，在不同预张力作用下的涤纶单丝中声波旅行8种起点距离的平均延迟时间，除了400 mm起点距离仅一个数据无法平均之外，平均延迟时间都随换能器隔距增大而略有增大趋势，而不完全是理论上的固有不变[6-7]。

表5 在不同预张力作用下的涤纶单丝中声波旅行8种起点距离Li的平均延迟时间T0 μs

2.2 两点倍长法结果计算

选用仪器支架能触及的（50 mm, 100 mm）、（100 mm, 200 mm）、（150 mm, 300 mm）、（200 mm,400 mm）4 个倍长组数据，分别陆续计算延迟时间T0、声速C和声模量E，再结合Cu进一步计算取向度F和取向角θ，结果详见表2、表3和表4。

表3 外推法和倍长法所测声速C和声模量E

表4 外推法和倍长法所测取向度F和取向角θ

2.3 预张力影响分析

试验结果显示，不同预张力下所测得的声波旅行时间TLi—换能器隔距Li散点数据与最小二乘法拟合直线高度相符，表明可由外推法计算仪器系统的延迟时间T0、纤维中的声速C、动态弹性模量E的准确值可靠。由表2 可知，在不同预张力下，延迟时间最大238 μs，最小226 μs，相差12 μs，测得值波动范围约为5%，表明它与试样预张力间也有一定的关联，整体呈现先变小、后变大规律，且在预张力0.089 cN/dtex时为极小值。

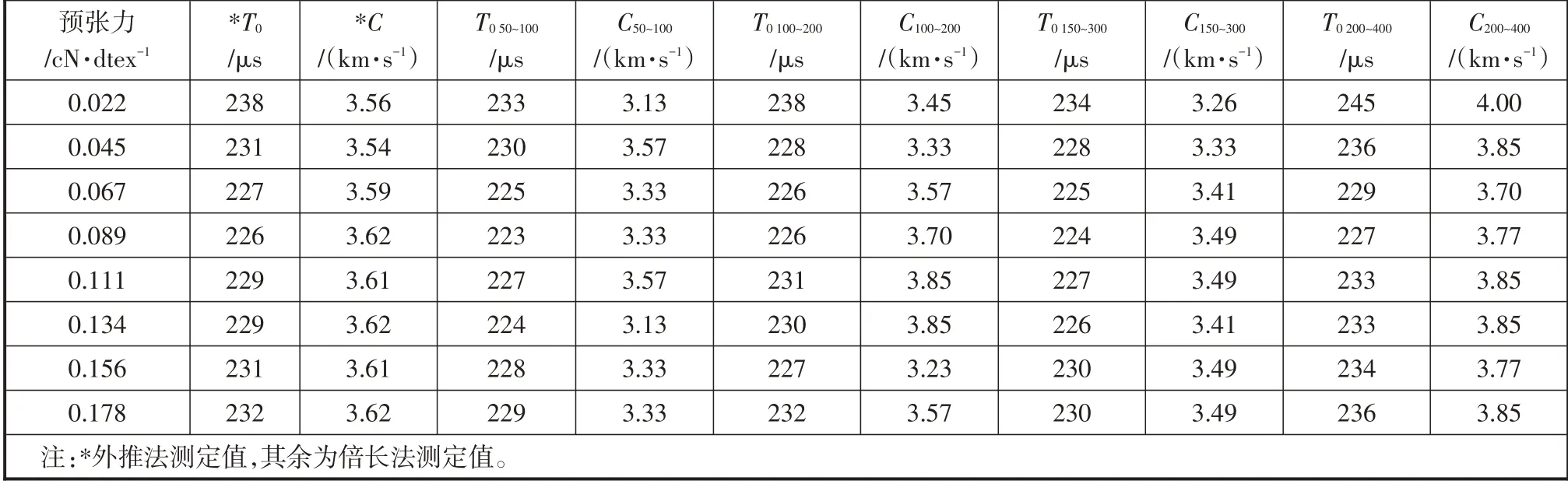
表2 外推法和倍长法所测延迟时间T0与声速C

根据表2、表3 和表4 数据作图2，可见优选的预张力为0.09～0.18 cN/dtex（过大张力潜在导致拉伸），在该区间的测定值趋于稳定，这与前期相关研究结果[10]和仪器说明书要求（0.1～0.2 gf/den）一致，即在试样保持平直但未被拉伸的前提下，随着预张力的增加，测定值趋于恒定。

图2 预张力对声速C、声模量E、取向度F测定值的影响

2.4 倍长法隔距优选

以预张力0.089 cN/dtex 为例，根据表2、表3 和表4数据作图3，与多点外推法结果（棱形实线五元环）相比，4组两点倍长法结果（圆点虚线五元环）最为接近，即优选的换能器隔距是100 mm和200 mm。这一结果与前期采用丙纶为试样进行的类似测定[10]和仪器说明书建议的200 mm 和400 mm 不同，说明倍长法隔距优选对试样品种存有一定的依赖性。

图3 延迟时间、声速、声模量和取向参数外推法与倍长法测定值的比选

2.5 方法标准化

现行关于声波在材料中传播速度和模量测定的相关国家标准有3 项。中科院声学所牛凤岐等编制的国标GB/T 18022—2000《声学1～10 MHz 频率范围内橡胶和塑料纵波声速与衰减系数的测量方法》，描述了采用插入取代法，即在测试水槽中，将被测材料（橡胶和塑料以及以它们为基料的复合材料）样品插在发射换能器与接收换能器之间平面波声束路径上，令其取代相同长度的水，借助于样品插入前后声脉冲信号传播时间和幅度的变化，从而测得该材料的声速和声衰减系数。该方法要求试样厚度大于10个波长，且测得值为径向声速，而非轴向声速，对纤维和薄膜等低维轻质材料无法适用。GB/T 38897—2020《无损检测弹性模量和泊松比的超声测量方法》和GB/T 23900—2009《无损检测材料超声速度测量方法》仅适用于块状固体材料，迫切需要解决适用于纺织纤维的类似方法的标准化研究。

现行国际标准化组织标准ISO 6721-9:2019《塑料—动态力学性能的测定—第9部分：拉伸振动—声脉冲传播法》（Plastics—Determination of dynamic mechanical properties—Part 9:Tensile vibration—Sonic-pulse propagation method）描述了声脉冲传播法测定聚合物拉伸存储模量E’（等效于动态弹性模量或声模量）的原理，所用声波为3～10 kHz的非连续频率声波。该方法适用于测量0.01～200 GPa的存储模量，在10 kHz时损耗因子低于0.1，其适用于测量薄膜或细纤维和长试样中的轴向声速，典型样条为薄膜300 mm×5 mm×0.1 mm（长×宽×厚）或纤维300 mm（长）×0.1 mm（直径）。但如需根据E=ρC2计算材料模量，还要进一步测定其密度，潜在干扰因素较多。

本试验所用试样为常规涤纶单丝（直径0.2 mm），前期工作中已用直径为0.16 mm 的普通丙纶单丝，且均已验证该方法可靠有效[10]，这也从侧面说明该方法已具备转化为制定国家标准的理论、技术、试验和设备基础。

综上所述，多点外推法通过测量波长远大于直径的声波在纤维中的纵向传播速度，巧妙利用纤维材料低维轻质特征，合理避开密度环节而仅用线密度即可精准地表达弹性模量并与分子取向结构参数相关联，无需分析拉伸曲线，实现试样无损可重复，操作简便、快捷、可靠，是传统准静态拉伸应力—应变曲线分析法的对等重要方法，不仅能用于传统化纤生产过程的例行监测以预判后续工艺设置和产品性能，还能用于高性能和生物纤维研发应用。

3 结论

（1）采用国产声速法纤维取向度/动态弹性模量测定仪，不同预张力下所测得的声波旅行时间-换能器隔距散点数据与最小二乘法拟合直线高度相符，表明由多点外推法计算仪器系统的延迟时间T0、纤维中的声速C、动态弹性模量E的准确、可靠；进一步可根据已知的无规取向声速值Cu计算赫尔曼取向因子F和取向角θ。此外，发现仪器延迟时间随换能器隔距增大而略有增加趋势，而不完全是理论上的固有不变。

（2）两点倍长法计算优选预张力为0.09～0.18 cN/dtex，换能器隔距为100 mm 和200 mm，其对试样品种存有一定依赖性，适合只需相对比较的工业应用和教学演示。

（3）多点外推法更适于精确定量科研，这些试验数据验证了声脉冲传播法测定纺织纤维的动态弹性模量的多点外推法标准化的可行性。