混合梁斜拉桥双悬臂施工塔梁临时固结有限元分析

温东昌， 高树威， 杨烨， 马超

(1.中交路桥华南工程有限公司， 广东 中山 528400；2.长沙理工大学 土木工程学院， 湖南 长沙 410114；3.苏交科集团股份有限公司， 江苏 南京 210000)

双悬臂施工具有节约成本、缩短工期的优点，在混合梁斜拉桥施工中应用广泛。如川藏公路迫龙沟大桥采用双悬臂施工，边跨预应力砼梁采用牵索挂篮悬臂浇筑，中跨结合梁由架梁吊机悬臂拼装。但由于混合梁斜拉桥边中跨主梁截面形式及材料自重不同，施工中易产生较大不平衡力矩，对塔梁固结的锚固措施要求较高。针对这一问题，该文以广东中开(中山—开平)高速公路银洲湖大桥双塔三跨斜拉桥为工程背景，利用ABAQUS有限元软件建立塔梁固结处空间模型，采用降温法模拟预应力筋，提取MIDAS/Civil整体计算模型中的内力作为边界条件，分析验证固结处的受力情况。

1 工程背景

1.1 结构总体布置

银洲湖大桥双塔三跨斜拉桥跨径布置为(188+530+188) m，全桥共4×24对斜拉索，钢混结合部位于中跨过主塔8.75 m处，梁中心线高3.5 m，全宽为36.4 m，顶面设置2%双向横坡，中跨采用PK箱形组合梁，边跨采用PK箱形砼梁。砼箱梁采用C55砼，钢箱梁采用Q345C钢。边跨砼梁采用牵索挂篮悬浇，中跨钢箱梁采用吊机悬臂拼装。主梁标准断面及索塔横断面见图1。

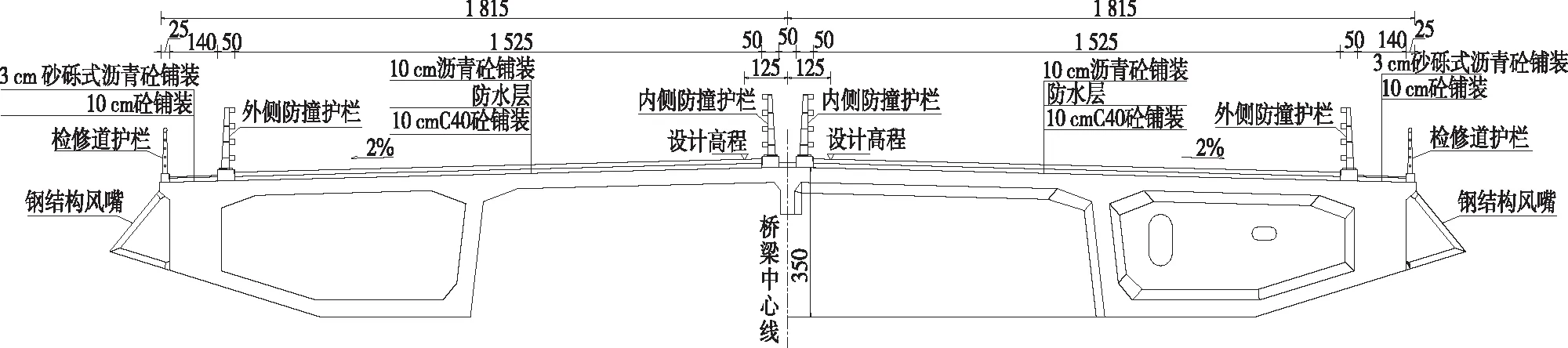
图1 砼箱梁标准断面(单位：cm)

主梁边跨施工至第8节段后，再悬臂浇筑一两个节段，即将主梁与施工临时辅助墩临时固结，以减小主梁施工悬臂长度。边中跨合龙后解除塔梁固结处的竖向预应力，解除塔梁临时固结。

1.2 塔梁临时固结措施

桥梁纵向采用半漂浮体系，索塔与主梁之间设置纵向限位约束装置。塔梁固结时，将8束φ15-17预应力钢绞线一端锚固在索塔下横梁内，穿过临时固结垫石和主梁边腹板在桥面进行张拉，以抵抗不平衡力矩。单侧索塔共设置4个固结垫石，张拉4×8根预应力束。临时固结断面见图2。

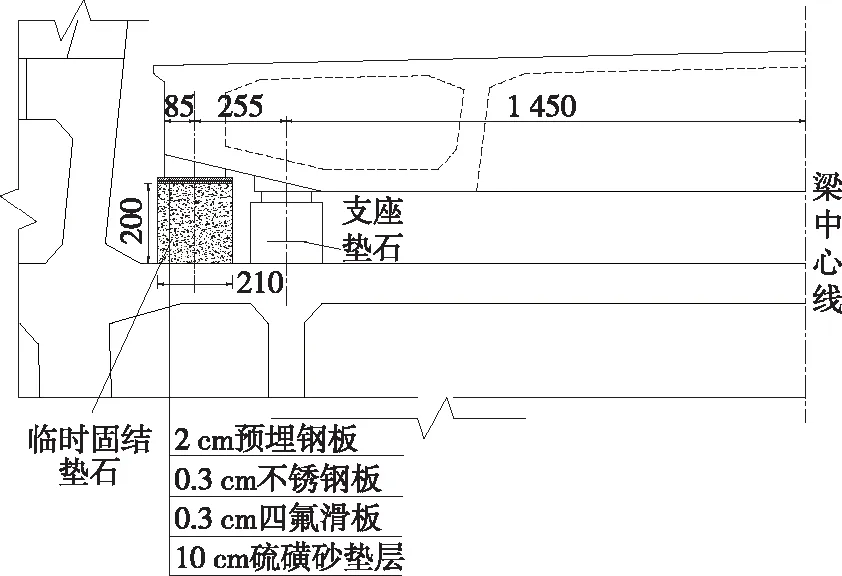
图2 塔梁临时固结纵断面示意图(单位：cm)

1.3 施工步骤

全桥主梁共划分24节段，边中跨主梁从第3节段开始进行双悬臂施工。施工步骤见图3。

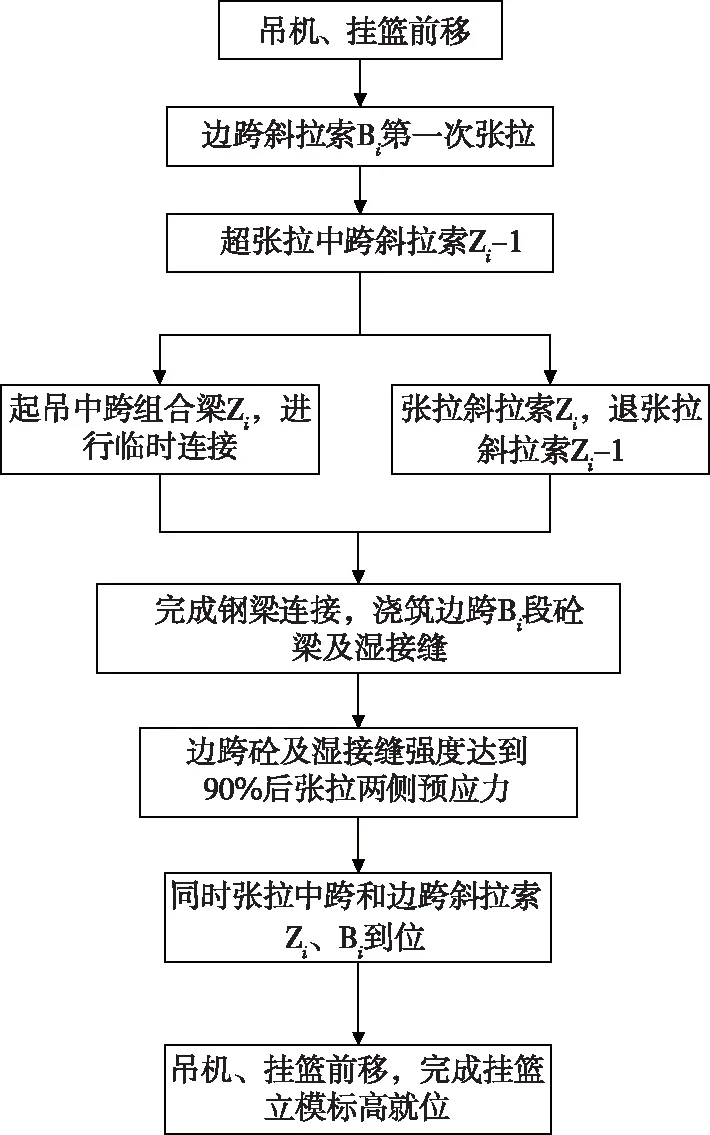
图3 桥梁施工流程

如图4所示，以临时固结垫石作为永久结构，塔梁固结时，在主梁纵向挡块与临时固结垫石之间以填充可靠措施的方式约束主梁纵向位移。

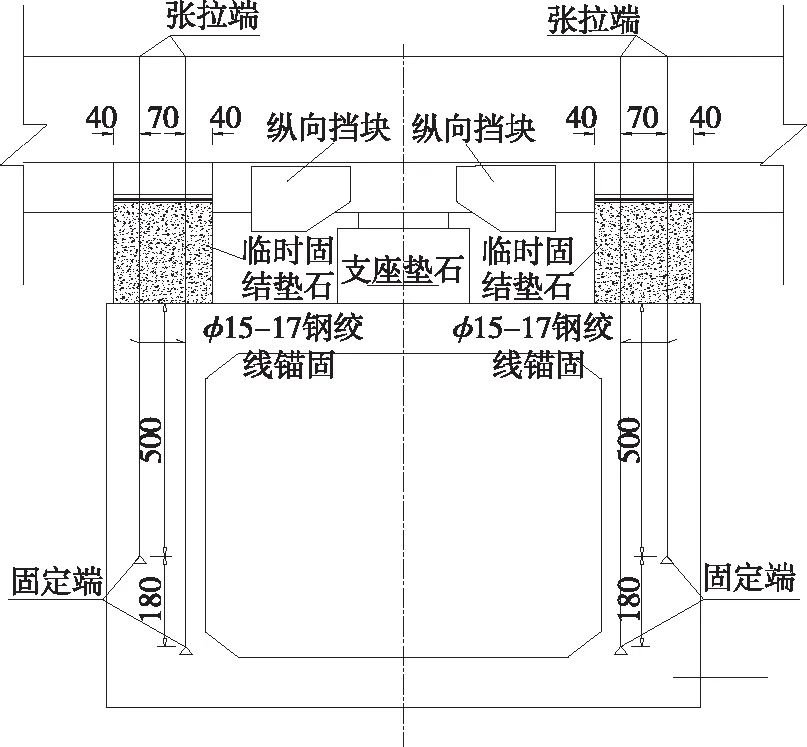
图4 塔梁临时固结横断面示意图(单位：cm)

2 全桥结构整体有限元分析

2.1 全桥整体有限元模型建立

除斜拉索外，其余结构全部采用梁单元模拟，桥塔底部固结约束，塔梁固结阶段索塔下横梁与主梁之间设置刚性连接。图5为全桥1/2结构有限元模型。

图5 全桥1/2结构有限元模型

2.2 模型计算结果

边跨砼梁及中跨砼桥面板应力计算结果见图6、图7。

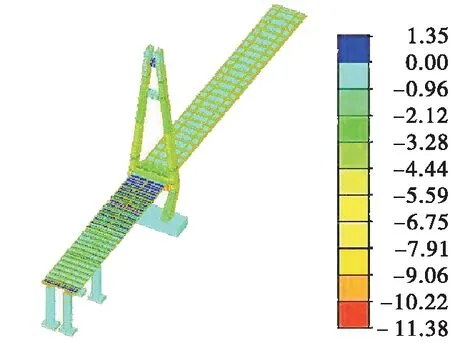
图6 索塔与边跨砼施工阶段最大应力(单位：MPa)

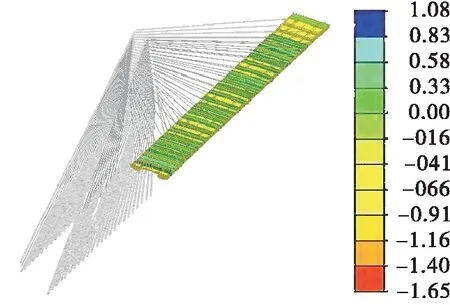
图7 索塔与中跨桥面板施工阶段最大应力(单位：MPa)

由图6、图7可知：施工阶段全桥砼梁和中跨砼桥面板最大应力不超过1.5 MPa，满足要求。

2.3 最大不平衡力矩工况

提取塔梁固结处主梁两端的内力，全桥共划分253个施工阶段，统计并筛选出最大不平衡力矩出现的工况，最后代入三维空间有限元模型进行分析。各工况下杆端内力情况见表1。

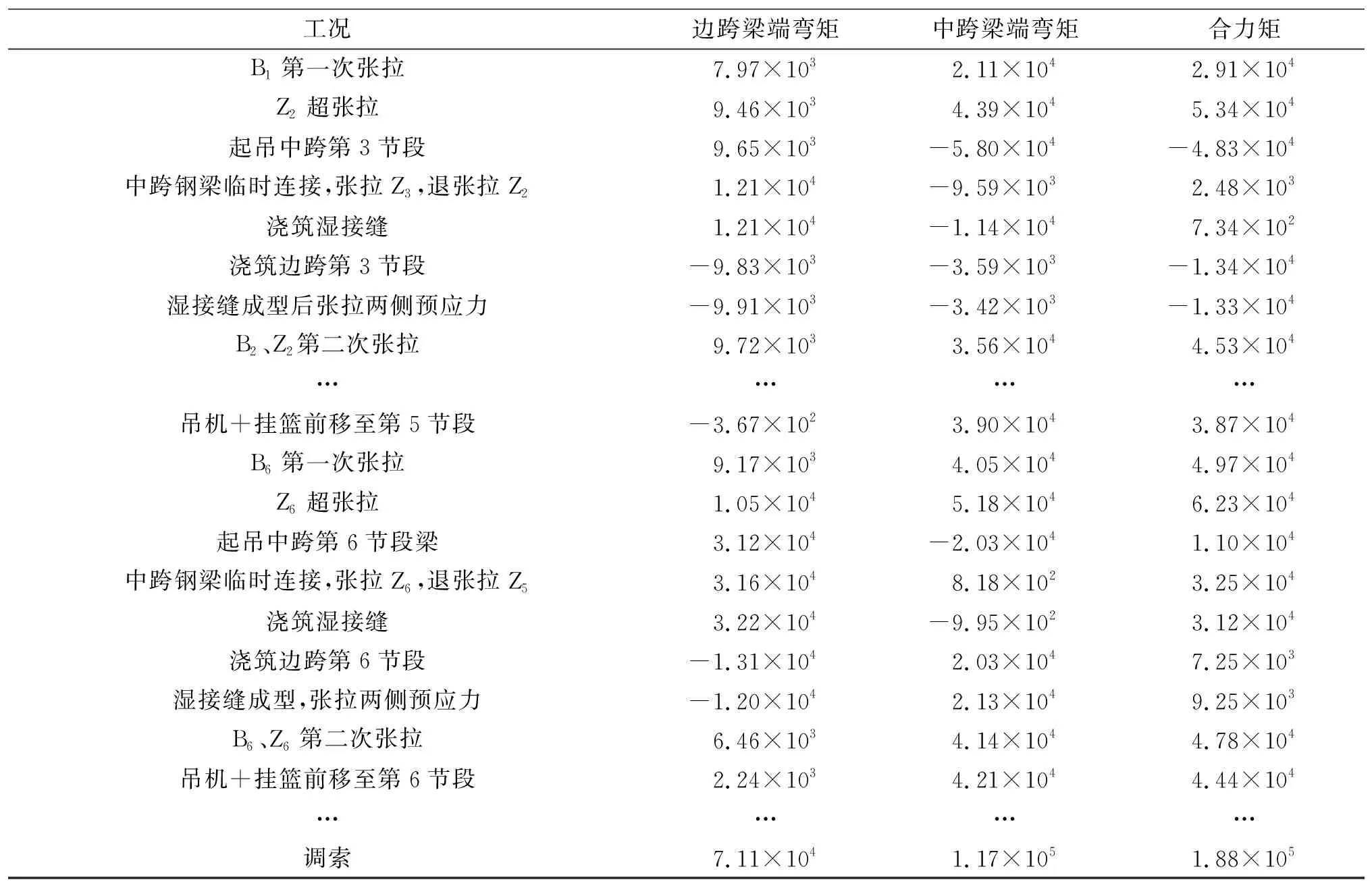
表1 最大不平衡力矩工况 kN·m

由表1可知：最大不平衡力矩出现在超张拉中跨第6对拉索时，最大不平衡力矩为62 300 kN·m。

3 塔梁固结空间有限元分析

3.1 模型选取范围

根据圣维南原理，若将物体的一部分边界上的面力变为分布不同但静力等效的面力(主矢量相同，对同一点的主矩也相同)，其近处的应力分布会受到显著影响，但远处所受影响可忽略不计。为使模型受力状况与实际受力状况接近，模型从远离固结区域选取，取边跨距离索塔中心线10.55 m处到中跨距离索塔中心线8.75 m处共19.3 m砼梁，索塔选取距下横梁顶面9.875 m段，下部结构取至距下横梁底面8.5 m段(见图8)。

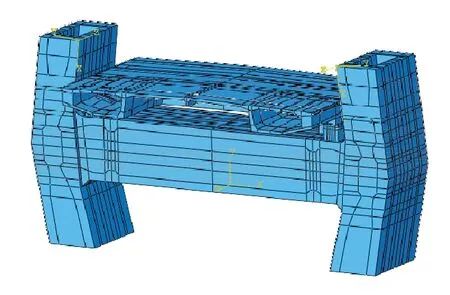
图8 塔梁固结有限元模型

3.2 模型约束条件

索塔底部采用全固结约束，索塔下横梁与主梁之间建立竖向与纵向约束，竖向由主梁与下横梁的支座垫石和临时固结垫石硬接触模拟，纵向由临时固结垫石与主梁纵向挡块之间的弹簧单元约束主梁纵向位移。模型竖向与纵向之间的约束见图9。

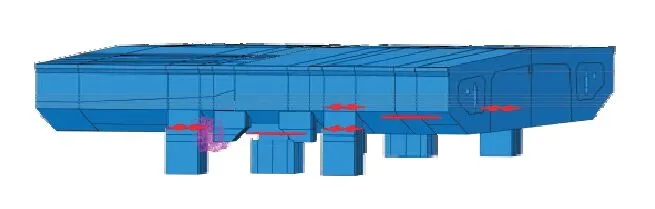
图9 塔梁竖向及纵向约束

3.3 模型荷载条件

(1) 通过MIDAS/Civil分析提取最不利荷载工况下杆端各项内力(见表2)。模型自重参数按照重力加速度9.8 m/s2施加在模型整体上。

(2) 预应力荷载。采用降温法对塔梁固结处施加预应力。其原理是温度降低时，预应力筋收缩，通过预应力筋与砼之间建立内置区域，使预应力筋与砼之间共节点，将预应力筋的收缩应变传递到砼区域。计算公式如下：

表2 最大不平衡力矩工况下杆端内力

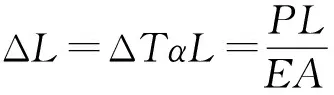
(1)

(2)

式中：α为预应力筋的线膨胀系数，α=1.2×10-5℃-1；E、A分别为预应力筋的弹性模量和横截面积；P为初始预应力值。

模型中预应力参数及降温计算结果见表3。

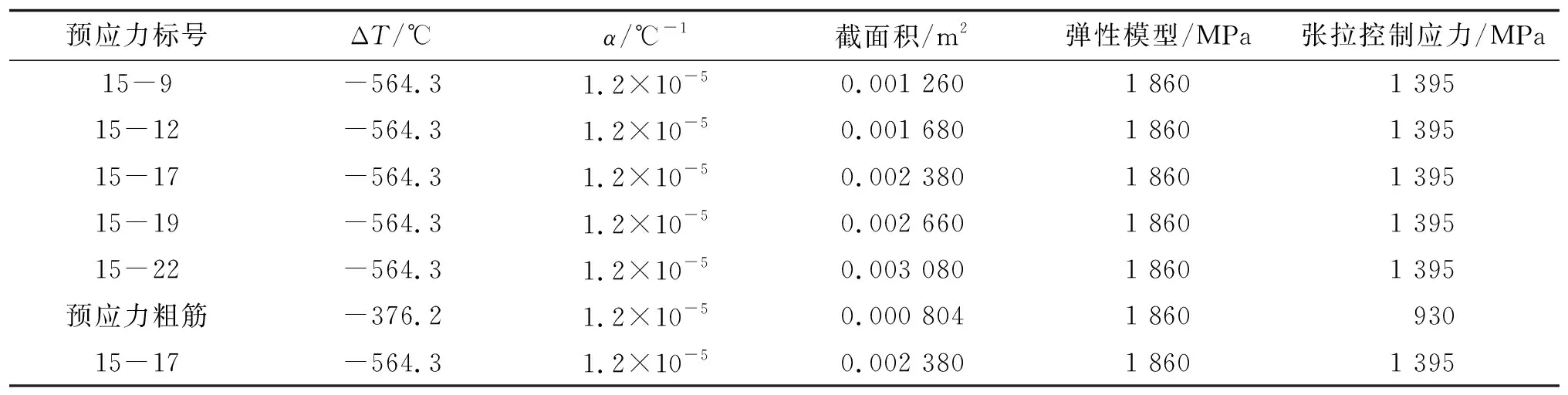
表3 预应力参数

考虑工程的实际情况，模型中用温度预定义场先设定所有预应力筋初始温度为20 ℃，再利用另一分析步定义所有预应力筋-564.3 ℃的降温值，使之产生收缩变形。模型中预应力布置及张拉情况见图10。

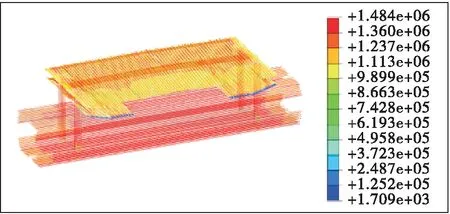
图10 塔梁固结处预应力布置及张拉情况(单位：kPa)

3.4 模型材料参数

模型中主梁采用C55砼，索塔采用C50砼，临时固结垫石顶层采用Q235钢板。模型中材料参数见表4。

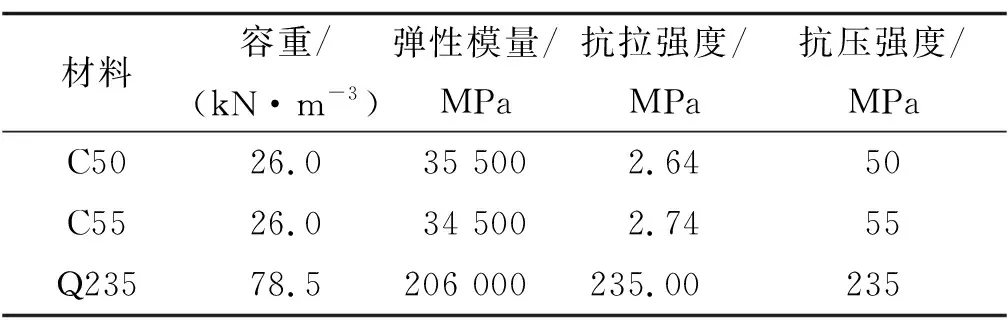
表4 模型中材料参数

3.5 模型网格划分

索塔采用C3D8R八节点线性六面体减缩积分单元，共150 000个单元；砼梁由于截面复杂程度较高，采用C3D8R八节点线性六面体减缩积分单元和C3D4四结点线性四面体单元混合，不同梁端之间采用绑定的方式连接。为使节点之间传力过渡平顺，参与绑定的几何体网格划分尺寸一致。预应力筋采用T3D2桁架单元，共80 000个单元，总体网格尺寸为0.3 m。模型整体网格划分见图11。

图11 模型网格划分

3.6 空间模型分析结果

代入荷载及位移边界条件后，经过初步计算，得到索塔、主梁应力和竖向位移(见图12～14)。

图12 索塔最大主应力云图(单位：kPa)

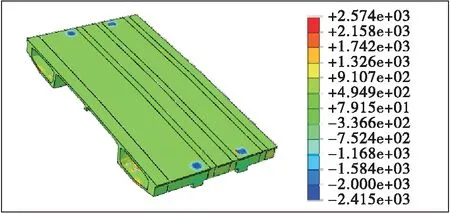
图13 砼梁最大主拉应力云图(单位：kPa)

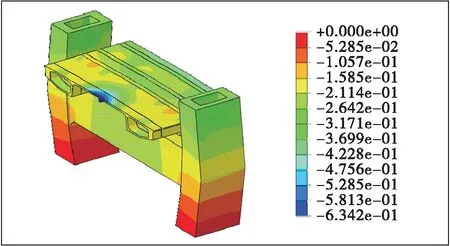
图14 索塔与砼梁竖向位移云图(单位：m)

由图12、图13可知：索塔最大拉应力为1.28 MPa，出现在下横梁根部，满足规范要求。主梁大部分拉应力不超过1.17 MPa，最大拉应力出现在边跨侧临时固结预应力束附近，具体位于主梁边跨段靠近实心段主梁的边腹板内侧与顶板过渡面相交处，最大值为2.57 MPa，小于材料的抗拉强度。出于安全考虑，可对局部结构加强构造配筋。

由图14可知：在两侧不平衡负弯矩作用下，主梁整体朝向中跨侧倾斜，使边跨侧相对位移呈向上的趋势。但临时固结的预应力筋抵抗了不平衡负弯矩的作用。由于标准段主梁截面顶板较薄，顶板与边腹板厚度差异较大，较厚的边腹板在固结预应力作用下位移趋势向下，较薄的顶板在不平衡负弯矩作用下位移呈向上的趋势，两处竖向位移趋势不同导致交界处有拉伸的趋势，使顶板向边腹板厚度过渡处容易产生应力集中。说明不平衡负弯矩对主梁安全较为不利。

除主梁与索塔外，其余固结措施的应力及位移见图15～18。

图15 主梁纵向挡块最大主应力云图(单位：kPa)

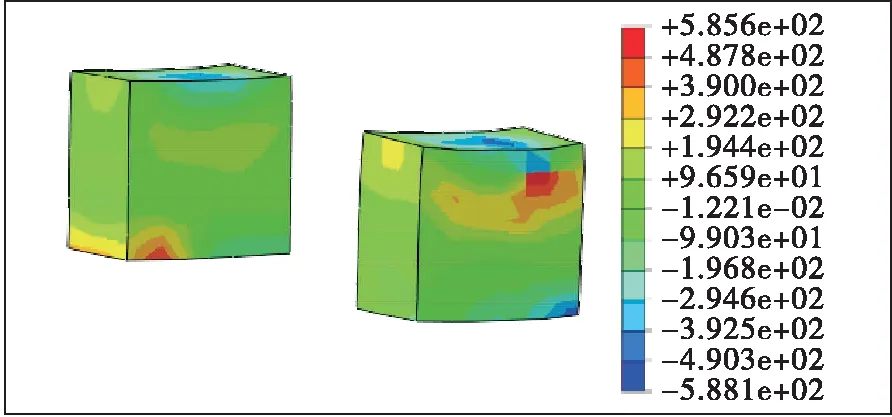
图16 临时固结垫石最大主应力云图(单位：kPa)

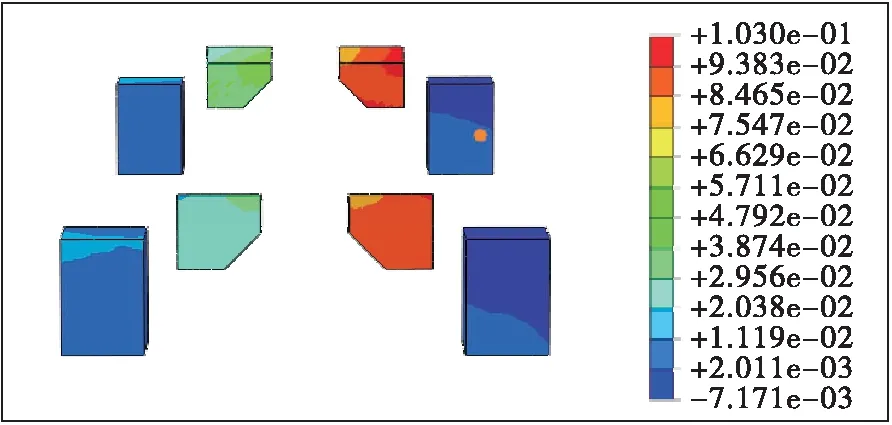
图17 固结垫石与纵向挡块纵向位移云图(单位：m)

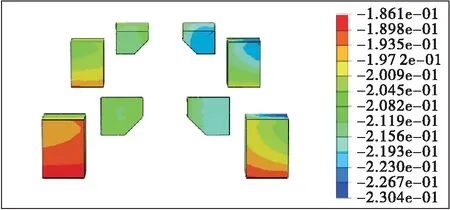
图18 固结垫石与纵向挡块竖向位移云图(单位：m)

由图15、图16可知：纵向挡块在不平衡力矩与水平力作用下出现局部应力集中，最大主拉应力为2.24 MPa，范围较小。出于安全考虑，可加强局部构造配筋。固结垫石最大主拉应力为0.59 MPa，满足要求。

由图17、图18可知：边跨侧固结垫石与纵向挡块的纵向位移略大于中跨侧，说明在不平衡水平力及不平衡力矩作用下边跨侧纵向挡块容易出现较大拉应力。

4 结论

(1) 塔梁固结处主梁和索塔结构受力均匀，传力明确。固结预应力与主梁内纵横竖向预应力能确保大部分结构在最大不平衡负弯矩及不平衡水平力作用下其应力处于合理范围。

(2) 主梁在不平衡力矩作用下存在一定应力集中，最大主拉应力为2.5 MPa,小于材料轴心抗拉强度标准值2.74 MPa，满足要求。出于安全考虑，可对局部结构适当加密钢筋。

(3) 主梁纵向挡块对抵挡主梁不平衡水平力起到主要作用，在最大不平衡力矩工况下最大拉应力为2.2 MPa，拉应力出现范围较浅，大部分拉应力出现在纵向挡块表面。可通过适当添加纤维材料提高纵向挡块的劈裂抗拉强度。