各向异性应力边界条件下不同方向裂缝的变形特征
2021-02-23冯月丽刘月田丁祖鹏毛小龙
冯月丽,刘月田*,丁祖鹏,陈 健,毛小龙
(1.中国石油大学(北京),油气资源与探测国家重点实验室,北京 102249;2.中海油研究总院有限责任公司,北京 100028)
裂缝内的流体压力可以承担和分散作用在裂缝壁面上的力,同时裂缝内流体压力的存在改变了基质的应力分布状态,进而对储层的力学性质造成影响。二维平面内任意角度裂缝壁面受到的法向应力不仅与有效应力有关,还与裂缝方位有关。诸多学者对裂缝的变形规律进行了研究,对裂缝应力敏感渗透率的表征,这些研究大部分采用实验数据拟合得到经验公式或引入渗透率模数。袁士义等[1]通过实验研究了低渗透裂缝性油藏开采过程中裂缝的变形特征及其对渗透率和油井产能的影响,其中裂缝变形特征的数学表征采用基于实验数据得到的应力敏感经验模型。曹耐等[2]针对裂缝型储层中不同类型的裂缝,分别设计和进行了5种裂缝贯穿程度、4种裂缝充填模式的致密岩心渗透率应力敏感实验,并分析了各种裂缝模式的岩心渗透率应力敏感性差异,该研究中使用经典的指数式来表征压力敏感。陈文滨等[3]借助三维激光扫描、物理模拟试验和数值模拟方法研究了存在张裂缝和剪裂缝时油井的生产差异,研究结果表明当地层中裂缝为剪裂缝时油井的产能大于张裂缝,该研究中的应力敏感特征分析主要基于物理实验研究。赵光宇[4]以高温高压裂缝型储层为研究对象,通过实验方法测定了不同围压下渗透率的应力敏感特征。刘礼军等[5]利用页岩油藏数值模拟器分析了页岩油藏中应力敏感效应对多级压裂水平井产能的影响,该研究中对应力敏感部分的处理同样采用的是经典的指数式。刘建仪等[6]结合多级压裂水平井特征和页岩吸附气特性,将应力敏感系数引入Forchheimer渗流方程,建立了考虑吸附和应力敏感的页岩气水平井二项式产能方程。张海勇等[7]通过改变孔隙压力试验,模拟测定微裂隙低渗透储层的应力敏感特征,应力敏感渗透率的数学表征基于渗透率模数。张艳玉等[8]、Kikani等[9]引入渗透率模数来表示介质变形对渗透率的影响。李勇明等[10]根据双重介质渗流理论,综合考虑页岩储层的吸附解吸、扩散运移、天然裂缝的应力敏感效应,建立了页岩储层的渗流模型,并编程计算出产能特征曲线,研究中应力敏感的表征形式同样为指数式。毛小龙等[11]从岩石颗粒的角度出发,在对Terzaghi和Skempton这2个经典有效应力原理深入分析的基础上,综合考虑颗粒变形和颗粒间变形,建立了精确计算孔隙压缩系数的新关系式,并进行了规律分析与实例验证。段慕白[12]基于裂缝表面形态理论基础,分析了常规裂缝特征的识别技术,利用Eascan-D光电岩心测量系统,开展了碳酸盐岩裂缝表面参数获取与分析、裂缝表面微凸体形貌特征描述实验,建立了裂缝表面及空间三维模型,继而分析了裂缝闭合变形机理。王鑫朋等[13]应用川东龙马溪组页岩进行测试渗透率各向异性和应力敏感性实验,实验结果表明,不同岩样的渗透率随有效应力的增大呈现指数递减的规律。张烨等[14]通过实验对龙马溪组页岩的应力敏感性进行评价,X射线衍射和全应力-应变结果表明龙马溪组页岩具有明显的硬脆性特征,破裂前曲线均呈现明显的线弹性变形。丁景晨[15]为了研究稠油油藏特有的应力敏感特征,分别采用室内岩心流动实验装置和 RUSKA 在线高压毛细管黏度测试仪,对稠油油藏岩心的渗透率应力敏感性和稠油的黏度应力敏感性进行了测试,结果表明:随着孔隙流体压力的降低,稠油油藏岩心的渗透率呈指数式降低,在实验基础上,建立了产能方程,方程中渗透率的应力敏感采用指数式表征。祝春生等[16]从室内实验和理论研究两方面出发,深入研究了低渗透储层的应力敏感特征及其变化规律,在此基础上,利用渗透率应力敏感系数,结合分形理论,建立了考虑岩石内部结构、外部有效应力变化等多种因素影响下的渗透率变化规律的方程。研究表明,由于孔隙结构的特殊性,有效应力变化对储层渗透率的影响较大,而对孔隙度的影响很小。
上述学者研究的应力敏感数学表征基本都需要介质变形系数,但该系数不易确定,在实际应用中存在一定的局限性。在实验中要实现裂缝角度可控,同时施加各向异性应力技术要求难度高。因此,有关各向异性应力条件下不同角度裂缝变形特征研究的成果还很少。
基于上述问题,分别从实验上和理论上对裂缝的压力敏感特征进行了详细的探讨,如在物理模拟实验中采用造缝容易、变形明显的相似多孔介质材料,实现了实验中裂缝参数可控;同时设计制作了特殊的实验容器,实现了施加在模型各个边界上的应力不同。并以容易测量的基本弹性参数为基础,建立了各向异性应力边界条件下裂缝的新型变形计算模型,在此基础上进一步给出了考虑裂缝应力敏感特征的裂缝系统渗透率和介质整体渗透率张量的计算方法。该模型可解决介质变形系数不易确定的问题,同时能够综合考虑多种因素对裂缝变形的影响,对预测各向异性条件下复杂裂缝网络的变形、计算裂缝性渗流介质的渗透率动态变化具有重要参考价值。
1 定应力边界裂缝动态渗透率模型建立
1.1 不同角度裂缝条数计算
取渗流单元内包含一组或多组平行裂缝的典型微元作为研究对象,该微元在下文中统称为特征单元体。如图1所示,建立参照直角坐标系xoy,裂缝走向与x轴的夹角为β(下标i表示第i组裂缝)。平面上裂缝间距为d,纵向上裂缝垂直贯穿整个单元体。特征单元体的宽和长均为L,高为h,单元体四周均为定应力边界,边界AD和BC上垂直施加的应力为σ2,AB和CD上垂直施加的应力为σ3。
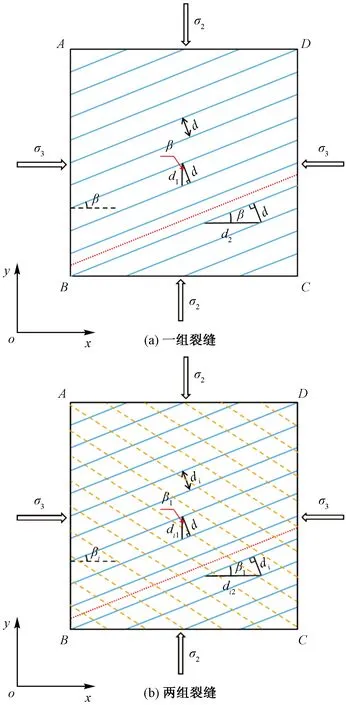
图1 裂缝分布理论模型示意图
如图1(a)所示,红色虚线左侧即AB边上的裂缝条数n1(取正整数)可计算为
n1=L/d1=Lcosβ/d
(1)
同理,CB边上的裂缝条数n2(取正整数)为
n2=L/d2=Lsinβ/d
(2)
则整个特征单元体包含的裂缝总条数n为
(3)
因此,当特征单元体内发育多组裂缝时,裂缝总条数[17]为
(4)
式中:n、n1、n2分别为特征单元内包含的总裂缝数、AB边上的裂缝条数、CB边上的裂缝条数;L为特征单元体的长和宽,m;d、d1、d2分别为垂直裂缝面方向的裂缝间距、AB边的裂缝间距(y方向)、CB边的裂缝间距(x方向),m;β为裂缝走向与x轴的夹角,(°);βi为第i组裂缝走向与x轴的夹角,(°);m为特征单元体内包含的裂缝组数,组;mt为特征单元体内包含m组裂缝时的总裂缝条数。
1.2 定应力边界条件下多角度裂缝渗透率计算模型
为建立裂缝变形计算模型,提出如下假设:①基质部分为各向同性线弹性体;②裂缝的应力-位移满足线性关系;③不考虑剪切应力的影响。
依据单条裂缝受力分析(图2),可求得倾斜角为β的裂缝面所承受法向应力(σn)为

图2 裂缝面受力分析
σn=σ2cos2β+σ3sin2β
(5)
结合有效应力原理[18]和模型假设可得单条裂缝的法向位移为
(6)
式(6)中:un为裂缝的法向位移,mm;b0为孔隙流体压力为p0状态下的初始裂缝开度,mm;σn为裂缝面受到的法向应力,MPa;σ2和σ3分别为模型x方向和y方向受到的法向应力,Mpa;Ef为裂缝系统弹性模量,MPa;αf为裂缝系统有效应力系数;β为裂缝倾斜角,(°);p为孔隙流体压力,MPa。
结合式(3)可得单元体内发育一组角度为β的裂缝时,裂缝系统的法向总位移为
uT=nun=Lb0(cosβ+sinβ)(σ2cos2β+
σ3sin2β-αfp)(dEf)-1
(7)
式(7)中:uT为裂缝系统的法向总位移,m。
同理,结合式(4)可得单元体内发育m组不同角度裂缝时,裂缝系统的法向总位移为
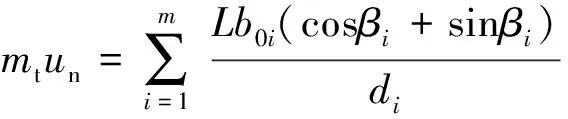
(8)
式(2)中:umT为单元体内发育m组不同角度裂缝时,裂缝系统的法向总位移,m;b0i为第i组裂缝的初始开度,m;di分别为第i组裂缝的裂缝间距,m;Efi为第i组裂缝系统弹性模量,MPa;αfi为第i组裂缝的裂缝系统有效应力系数。
从而,裂缝系统变形后开度(b)如下。
一组缝:

(9)
式(9)中:bT为一组裂缝的总开度,m。
多组缝:

(10)
式(10)中:bmT为多组裂缝的总开度,m。
多组裂缝的内蕴渗透率(kffm)为[19]
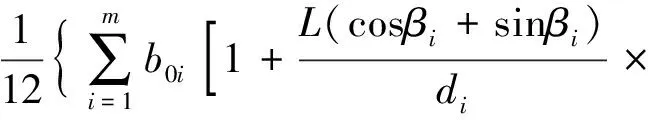
(11)
式(11)中:kffm为单元体内包含多组裂缝时的总的内蕴渗透率,m。
由孔隙流体压力为p0时的裂缝渗透率(k0)和孔隙流体压力为p时的裂缝渗透率(k)与裂缝开度的关系[20]为
(12)
式(12)中:k为孔隙流体压力为p时的裂缝渗透率,10-3μm2;k0为孔隙流体压力为p0时的裂缝渗透率,10-3μm2;Δb为流体压力变化时的裂缝开度变化量,m。
可得特征单元体平行裂缝方向的裂缝渗透率(没有特殊说明裂缝渗透率均指平行裂缝方向的值)为
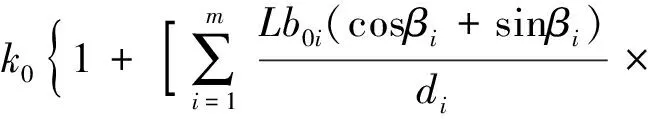
(13)
式(13)中:kf为裂缝系统渗透率,10-3μm2。
再以裂缝发育方向为x′轴建立裂缝直角坐标系x′o′y′,假设基质渗透率为km,则单元体的渗透率张量可表示为
(14)
式(14)中:K′为x′o′y′参照坐标系下的单元体的渗透率张量。
将其转换为xoy参照坐标系下的渗透率张量,表达式为[21]
(15)
式(15)中:K为xoy参照坐标系下的单元体的渗透率张量。
裂缝性渗流介质为各向异性渗流介质,当典型单元体内裂缝密度足够大时,其渗流效果可等效为各向同性渗流介质,等效的各向同性介质渗透率为
(16)
式(16)中:K为等效各向同性介质渗透率,10-3μm2;kx、ky分别为各向同性介质x方向和y方向的渗透率,10-3μm2;km为基质系统渗透率,10-3μm2。
等效前后渗流边界发生变化,但流量不变,即各向异性渗流介质和各向同性渗流介质的流量相等,即
(17)
式(17)中:Qani为等效各向同性介质的流量,mL/min;Qiso为各向异性介质的流量,mL/min;Wiso为各向异性介质的模型宽度,m;hiso为各向异性介质的模型厚度,m;Liso为各向异性介质的模型长度,m;μ为流体黏度,mPa·s;ΔP为流体压力变化量,MPa。
当裂缝密度不够大时,裂缝各向异性介质就不能等效为各向同性介质,流量只能通过数值方法来计算。
2 物理模拟验证理论模型
为验证上述计算模型的正确性,设计了两种实验方案。方案1:裂缝与驱替方向平行[图3(a)];方案2:裂缝与驱替方向呈45°角[图3(b)]。在上述两个方案中,模型四周均施加了各向异性应力。模型主要物理参数如表1所示。基质部分为各向同性应变介质,实验流体为单相蒸馏水。实验中通过改变模型中的平均孔隙流体压力,研究不同应力边界条件下,裂缝的开度变化及其对流量的影响。

表1 裂缝性渗流介质主要物理参数

图3 实验模型示意图
由图4(a)、图4(b)可看出,实验测试和理论计算结果一致性好,说明建立的裂缝渗透率计算模型是合理的、可靠的,可以用来计算定应力边界条件下的裂缝变形量及裂缝渗透率随孔隙流体压力、边界应力的变化规律。
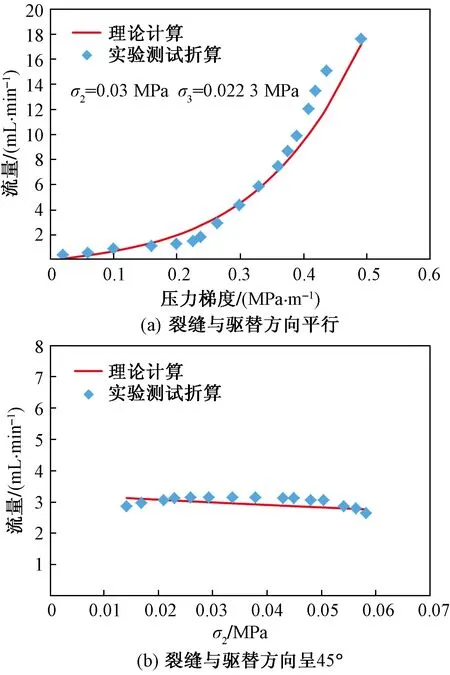
图4 实验实测折算与理论计算值对比
3 裂缝变形特征及全张量渗透率主值变化规律
基于建立的定应力边界应力敏感方程,研究各向异性应力作用下不同角度裂缝变形特征的影响因素及其对裂缝渗透率的影响。
3.1 裂缝变形特征及其影响因素
3.1.1 裂缝角度β
如图5所示,裂缝面与最大应力方向夹角越小,作用在裂缝面上的法向压应力越小,当孔隙流体压力增大时,裂缝开度减小量越小,因此,裂缝性渗流介质四周加载各向异性应力,与最大主应力方向夹角越小的裂缝渗透率越大。
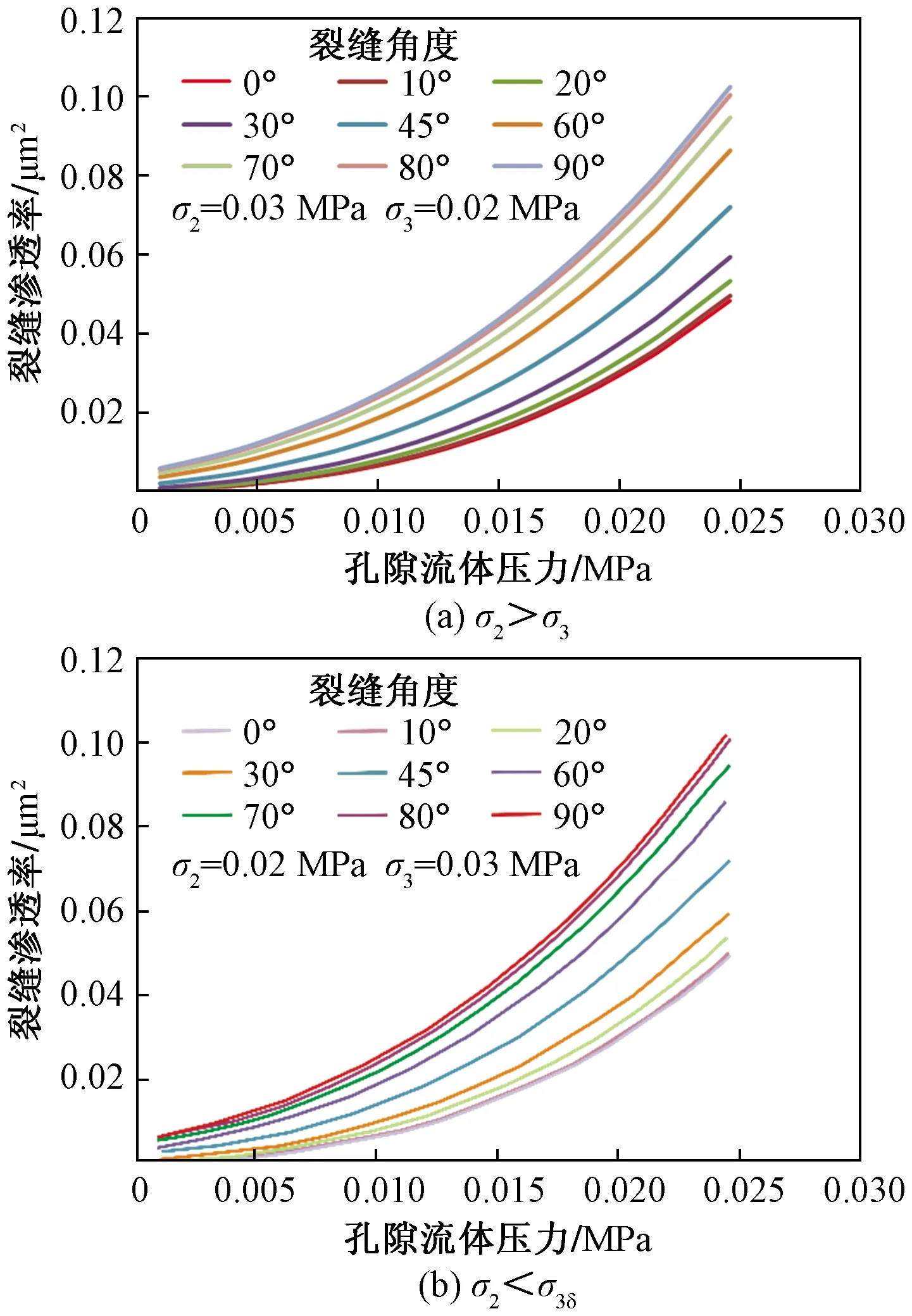
图5 裂缝角度对裂缝渗透率的影响
3.1.2 初始裂缝开度b0
如图6所示,裂缝初始开度越大,相同压力梯度下随孔隙流体压力增大裂缝变形后渗透率增大。这是因为,相同的有效应力变化量使得裂缝发生的应变相同,初始裂缝开度越大,裂缝面发生的位移量越大。
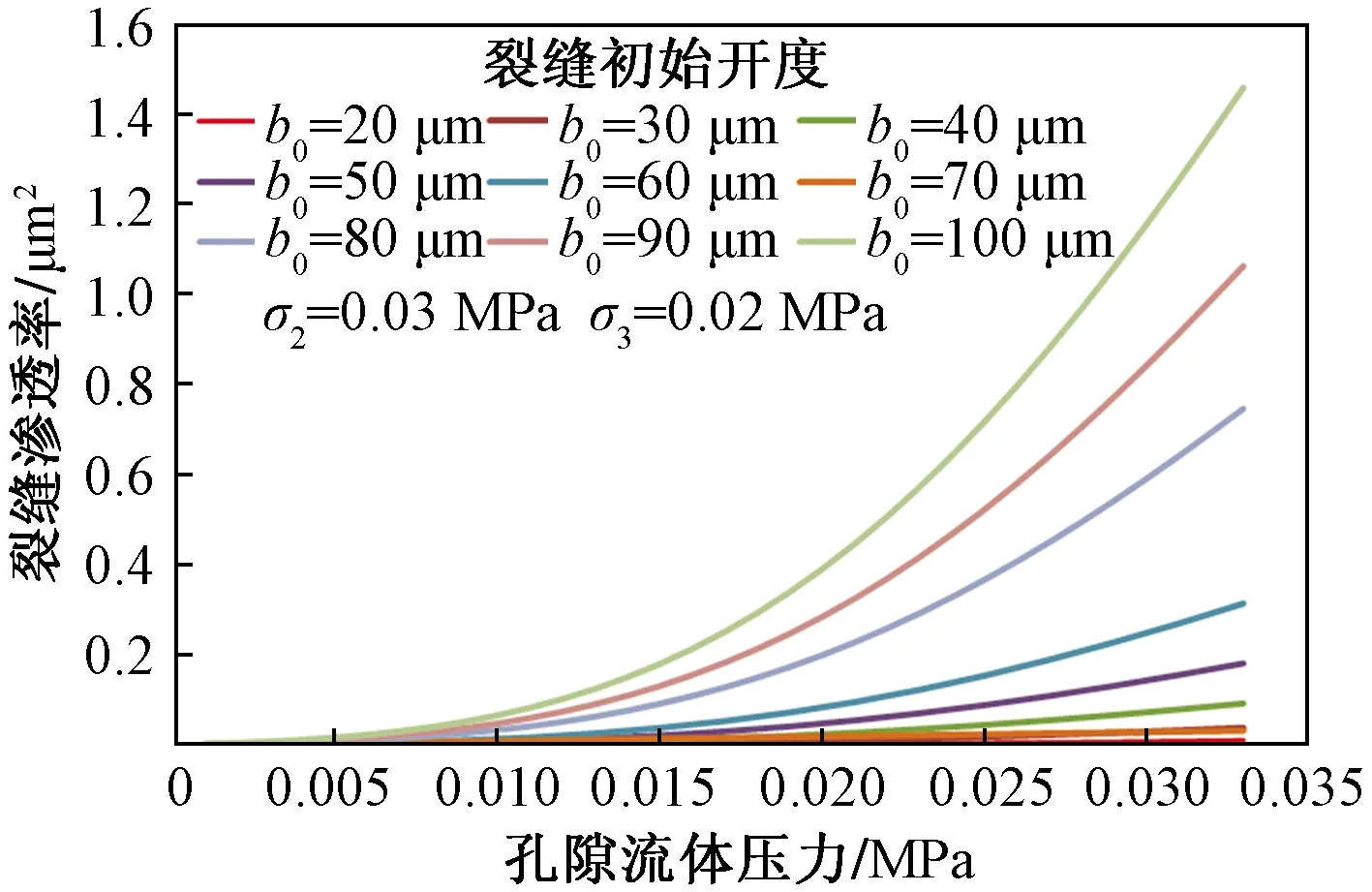
图6 裂缝初始开度对裂缝渗透率的影响
3.1.3 有效应力系数αf
如图7所示,根据有效应力原理,裂缝系统的有效应力系数αf越大,则作用在裂缝面上的法向压应力越小,从而裂缝变形量越小,因此,裂缝系统的有效应力系数αf越大,变形后裂缝渗透率越小。
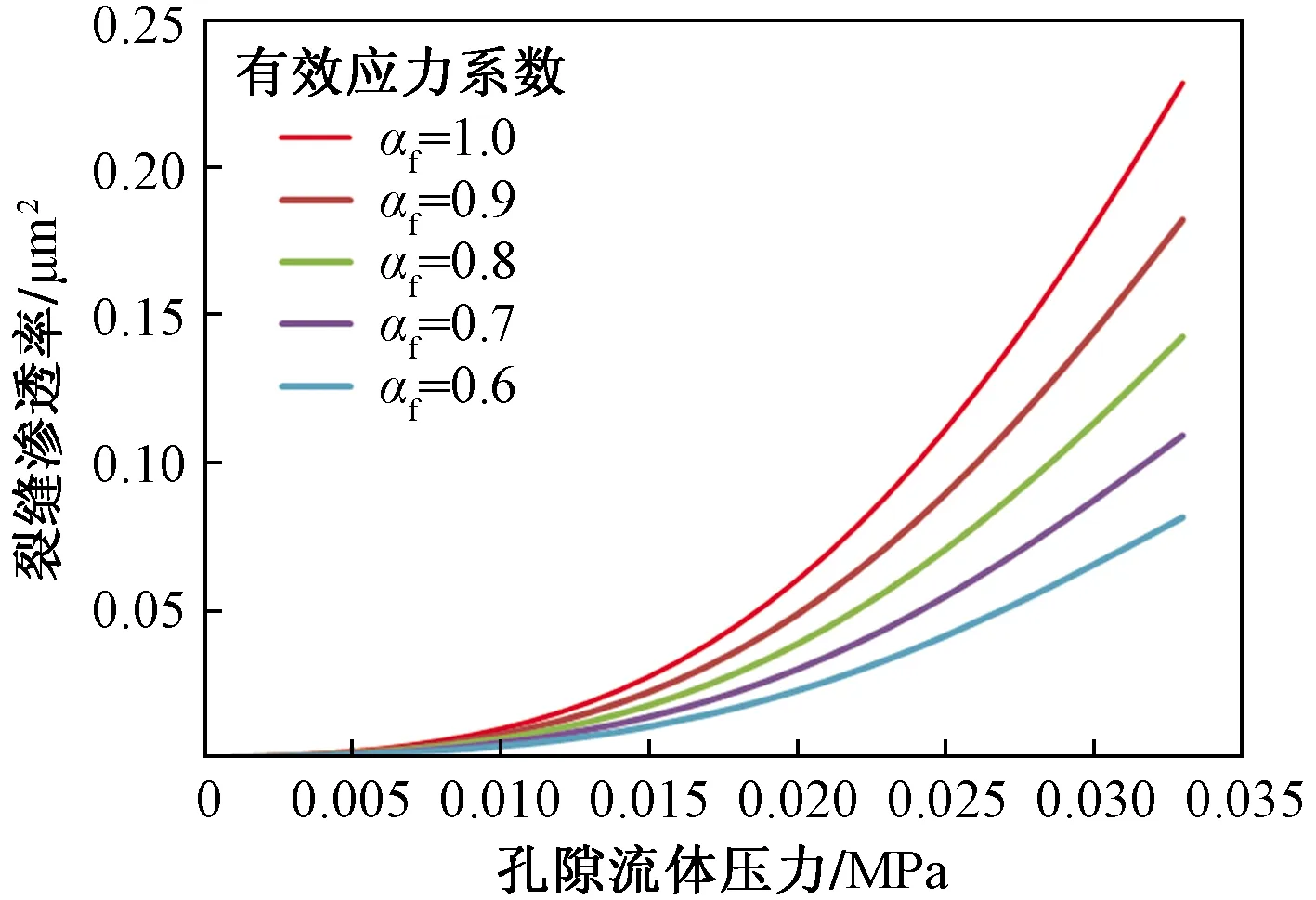
图7 有效应力系数对裂缝渗透率的影响
3.1.4 裂缝弹性模量Ef
如图8所示,裂缝弹性模量越大,裂缝面承受相同大小有效应力时,发生位移越小,裂缝开度保持较大,因此裂缝渗透率大。
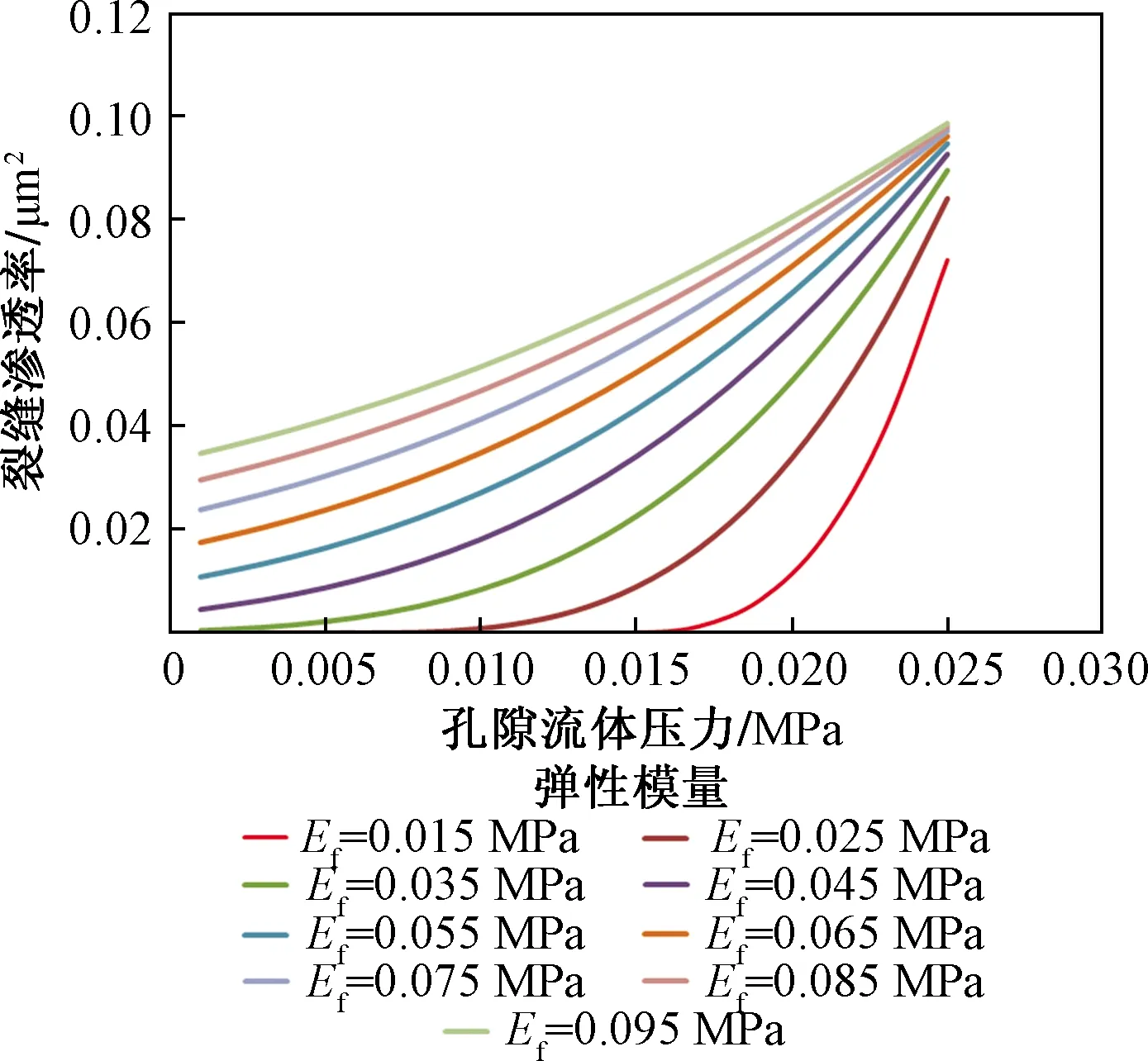
图8 弹性模量对裂缝渗透率的影响
3.1.5 边界应力σ2
如图9所示,应力σ2越大,裂缝面受到的总的有效应力越大,裂缝面发生的位移越大,因此裂缝渗透率越小。
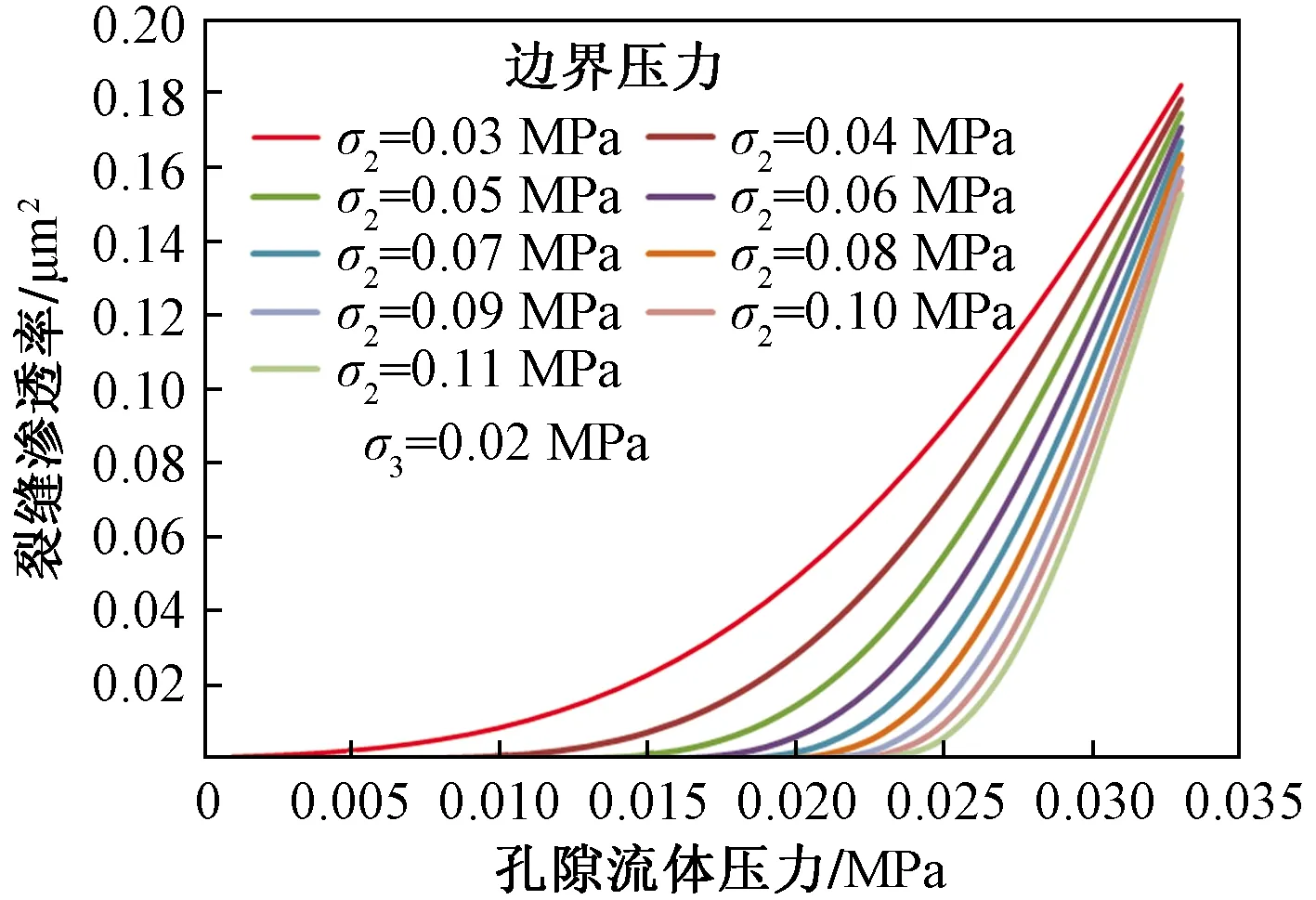
图9 σ2对裂缝渗透率的影响
3.2 包含多组裂缝的全张量渗透率变化规律
以图10所示的4种裂缝分布情况为例来研究定应力边界条件下储层发育多组裂缝时,其渗透率主值的变化规律。
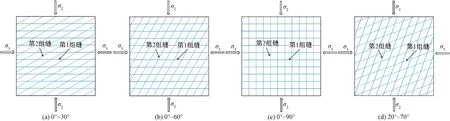
图10 两组裂缝模型示意图
3.2.1 裂缝角度β
如图11所示,定应力边界条件下,当特征微元体内发育两组不对称分布的裂缝时,随流体压力增大,渗透率主值变大,渗透率主值方向逐渐偏向压力敏感性强的那组裂缝[图11(a)、图11(b)];当两组裂缝正交分布[图11(c)],或两组裂缝角度之和为90°时,只有主值大小会发生变化[图11(d)]。
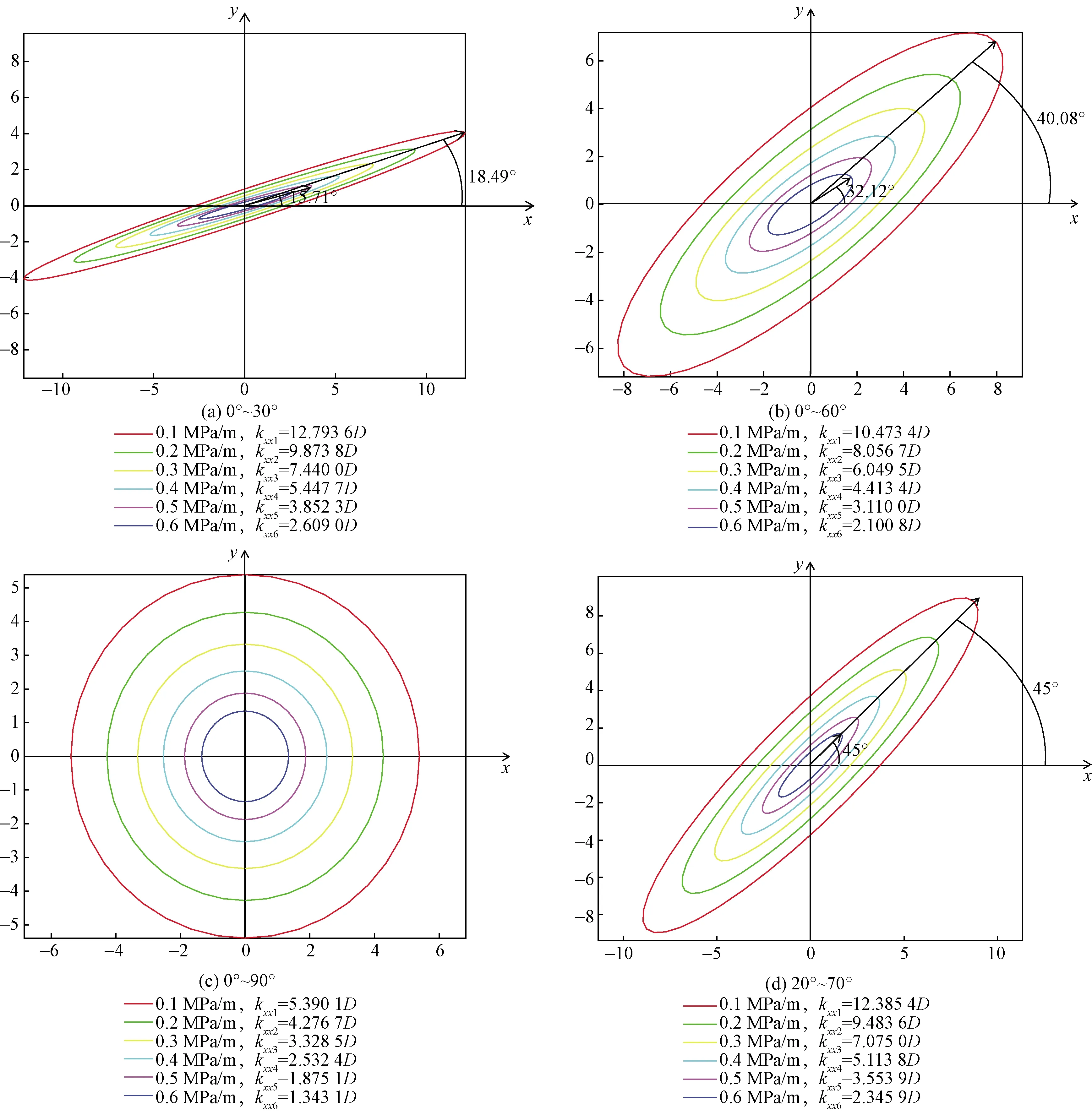
kxx为渗透率最大值
3.2.2 裂缝间距d
如图12所示,两组裂缝间距相等时,渗透率主值方向会偏向应力敏感性较强的那组裂缝,而当裂缝间距不等,裂缝条数相等时,渗透率主值方向始终沿着两组裂缝的角平分线方向。
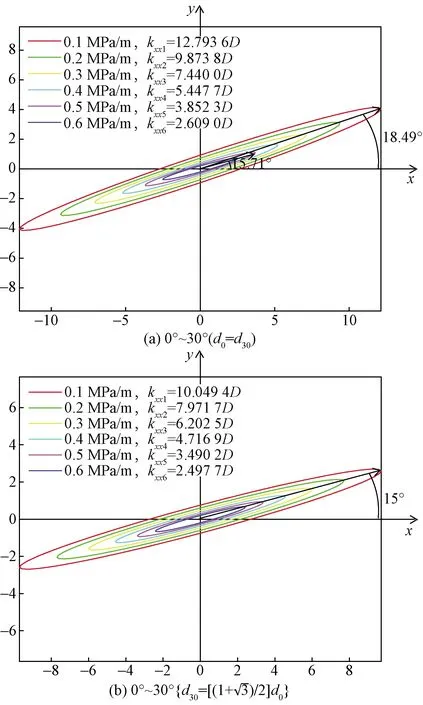
图12 两组裂缝间距对渗透率主值影响变化
3.2.3 裂缝弹性模量Ef
如图13所示,两组裂缝非正交分布时渗透率主值方向总是偏向弹性模量较小的那组裂缝;两组裂缝正交分布时,渗透率最大主值方向始终平行于弹性模量较小的那组裂缝。

图13 两组裂缝弹性模量对渗透率主值影响变化
4 结论
(1)基于各向同性线弹性体变形理论和裂缝面受力分析,建立了各向异性应力边界裂缝动态渗透率计算模型,并开展了相似多孔介质微观物理模拟实验。结果表明:实验测试值和理论模型计算结果具有很好的一致性,验证了各向异性应力边界条件下多角度裂缝动态渗透率模型的准确性和实用性。该模型能全面考虑裂缝系统和基质系统的弹性参数,相较于常用的经验公式,基础参数更易确定,且能用于计算不同应力边界时的裂缝变形量和渗透率,适用性更广泛。
(2)裂缝性渗流介质加载各向异性应力时,与最大主应力方向夹角越小的裂缝渗透率越大;裂缝初始开度越大,相同压力梯度下随孔隙流体压力增大裂缝变形后渗透率越大;根据有效应力原理,裂缝系统的有效应力系数越大,裂缝变形后渗透率越小;裂缝弹性模量越大,裂缝面承受相同大小有效应力时,发生位移越小,裂缝变形后渗透率越大;应力σ2越大,裂缝面受到的总有效应力越大,裂缝面发生的位移越大,裂缝变形后渗透率越小。
(3)定应力边界条件下,两组裂缝不对称分布时,随流体压力增大,裂缝系统渗透率主值变大,渗透率主值方向逐渐偏向应力敏感性强的那组裂缝,当两组裂缝正交分布时,只有主值大小会发生变化,最大主值方向始终平行于弹性模量较小的那组裂缝;两组裂缝等间距分布时,渗透率主值方向会偏向应力敏感性较强的那组裂缝,而当裂缝间距不等裂缝条数相等时,渗透率主值方向始终沿着两组裂缝的角平分线方向。
