局部双层去顶网壳参数化设计与力学分析
2021-02-23曹俊超黄丽丽鹿晓阳李大勇
曹俊超,黄丽丽,鹿晓阳*,李大勇,种 帅
(1.山东建筑大学工程力学研究所, 济南 250101;2.山东建筑大学材料学院, 济南 250101;3.山东建筑大学教务处,济南 250101)
近年来,大跨空间结构在中外的发展十分迅猛,从而涌现出了许多新型的空间网格形式[1]。其中就包括去顶网壳这一形式新颖的空间曲面网格结构。去顶网壳具有形制美观、力流传递合理等特点[2],具有广阔的工程应用前景和发展空间。很多学者均对去顶网壳结构进行了深入的分析和探讨,其参数化建模方法以及受力性能的相关研究已经较为全面。Lu等[3]研究了6类单层去顶网壳的节点与杆件分布规律,编写了6类结构相应的参数化模型设计程序,为单层去顶网壳的静、动力分析奠定了基础;董石麟等[4]提出了葵花型去顶网壳的简化计算模型,建立了该去顶结构的基本力学方程式,揭示了其力学特性;丁伟伦等[5]分析了吕梁新城体育中心体育场这一实际工程中的单层去顶网壳结构的稳定性,得出了该结构在静力作用下的稳定性能较好且符合规范标准的结论;林训潮[6]研究了不同几何参数下的单层去顶网壳结构的静力响应及其稳定性,提出了结构在稳定分析时的缺陷施加方法和对去顶部分的局部加强方案;宫仁国[7]探究了不同矢跨比等参数对单层去顶网壳自振性能的影响规律,得出了矢跨比变化与结构自振频率成正比的结论;宋波等[8]通过探究多维地震对双层去顶球面网壳的影响,提出去顶结构顶部的开口构造对网壳抗震性能的影响十分显著。去顶网壳结构可以满足大多数露天结构的需求,但单层去顶网壳不能很好地应用于大跨度空间结构。通过对单层去顶网壳下部合理增加杆件来对网壳进行局部加强,进而形成的局部双层去顶球面网壳无论是结构强度还是刚度均得到了大幅度提升,力学性能更为合理;且结构用钢量小于双层去顶网壳结构,造价相对更低,故而具有较大的发展潜力。
现通过探究6类局部双层去顶网壳杆件与节点的分布、连接规律,应用APDL程序设计语句编写设计6类局部双层去顶网壳结构相应的参数化模型设计程序,并在此基础上应用有限元软件对6类大跨度去顶网壳结构的受力特点及其主要几何参数对相应结构的力学性能影响规律进行了对比分析和研究。
1 局部双层去顶网壳建模设计
网壳在选型优化设计、力学性能研究时,多次建模极为耗费时间[9-10]。故探讨不同类型网壳结构杆件和节点的分布规律,应用APDL语句研究基于单层去顶球面网壳[3]的参数化设计方法,可提高结构设计、受力性能分析和选型优化设计效率[11]。
1.1 结构主要几何参数
局部双层去顶球面网壳包括跨度(S)、矢高(f)、网壳厚度(T)、对称区域数(Kn)、节点总圈数(Nx)、去顶圈数(Ns)等主要几何参数。结构曲率半径(R)及相邻两环对应的圆心角(Dpha)分别为
(1)
(2)
以肋环型局部双层去顶网壳为例,给出结构及主要参数示意图,如图1所示。

图1 肋环型局部双层去顶球面网壳及主要参数示意图
1.2 局部双层形式及位置
基于局部双层网壳模型[12],局部双层去顶结构是通过在去顶结构为基础的模型上层径向杆下添加下层径向杆、下层环向杆和腹杆等相应的杆件所组成的封闭三维体系,从而形成造型美观、力流传递较为合理的局部双层去顶结构。
肋环型和施威德勒型网壳的局部双层结构是由下层径向、环向杆和腹杆所组成的封闭三维桁架体系;联方型的局部双层结构是由位于主肋下的三角锥体系所构成的封闭三维体系;其余3种网壳的局部双层结构是由位于主肋下的角锥体系所构成的封闭三维体系。
6种网壳的结构形式简洁美观,既满足了人们对露天结构的需求,又有用钢量小、造价成本相对较低的优点,故而具有较大的实际工程应用前景。图2给出6种局部双层去顶网壳的局部加强结构模型图。

图2 6种局部双层结构
1.3 局部双层去顶球面网壳建模程序设计
局部双层去顶网壳根据杆件组合方式的差异可分成包括肋环型在内的6类较为常见的网壳结构类型,分别对应研究编写了6类去顶网壳的建模设计程序。以下仅以肋环型结构为例,介绍参数化设计方法。
1.3.1 确定输入控制参数
确定S、f、Kn、Nx、Ns、T等主要几何控制参数。
1.3.2 据上述参数确定节点编号及其坐标
(1)上层节点编号及其坐标:结构第i圈(Ns≤i≤Nx)第j对称区(1≤j≤Kn)所属节点编号数值可由下述表达式1+j+Kn(i-1)给出;对应的上层节点坐标为(R,360(j-1)/Kn,90-iDpha)。
(2)下层节点编号及其坐标:下层节点依旧由Ns圈开始建立,由表达式2+j+Kn(i+Nx-1)给出结构相应的下层节点编号,与之对应的节点坐标为(R-T,360(j-1)/Kn,90-iDpha)。
1.3.3 上层杆件连接
(1)上层环向杆连接:结构第i圈(Ns≤i≤Nx)第j对称区(1≤j≤Kn-1)环向杆由节点编号为j+1+Kn(i-1)与j+Kn(i-1)+2的节点相连,第i圈最后一对称区环向杆由节点编号为1+Kni与2+(i-1)Kn的节点相连而成。
(2)上层径向杆连接:第j对称区(1≤j≤Kn)第i圈(Ns≤i≤Nx-1)径向杆分别由节点编号表达式为1+j+Kn(i-1)与1+j+Kni的节点相互连接而成。
1.3.4 下层杆件连接
(1)下层径向杆连接:第i圈(Ns≤i≤Nx-1)第j对称区(1≤j≤Kn)下层径向杆由编号表达式为2+j+Kn(i+Nx)和2+j+Kn(i+Nx-1)的节点相连。
(2)下层环向杆连接:下层节点编号表达式为2+j+Kn(i+1+Nx)和3+j+Kn(i+Nx+1)的节点连接形成下层环向杆。
(3)下层腹杆连接:第j对称区(1≤j≤Kn-1)第i圈(Ns≤i≤Nx)下层腹杆分别由节点编号为1+j+Kn(i-1)和2+j+Kn(i+Nx-1)、Kni+1和2+(Nx+i)Kn的节点对应相连而成。
1.3.5 施加边界约束和节点荷载
因节点号是由内向外逐次递增,故而上层最后一圈的开始编号可由1+(Nx-1)Kn求出,编号小于该节点的布置均布载荷,大于等于该编号的节点据工程需要施加可动铰或固定铰约束节点位移。
1.4 6种网壳结构建模实例
短程线型选取Kn=5;三向格子与凯威特型网壳结构均选取Kn=6;其余3种网壳选取Kn=26。当结构的S=120 m、f=45 m、Nx=6、T=2.5 m、Ns=3时,结构建模实例如图3所示。
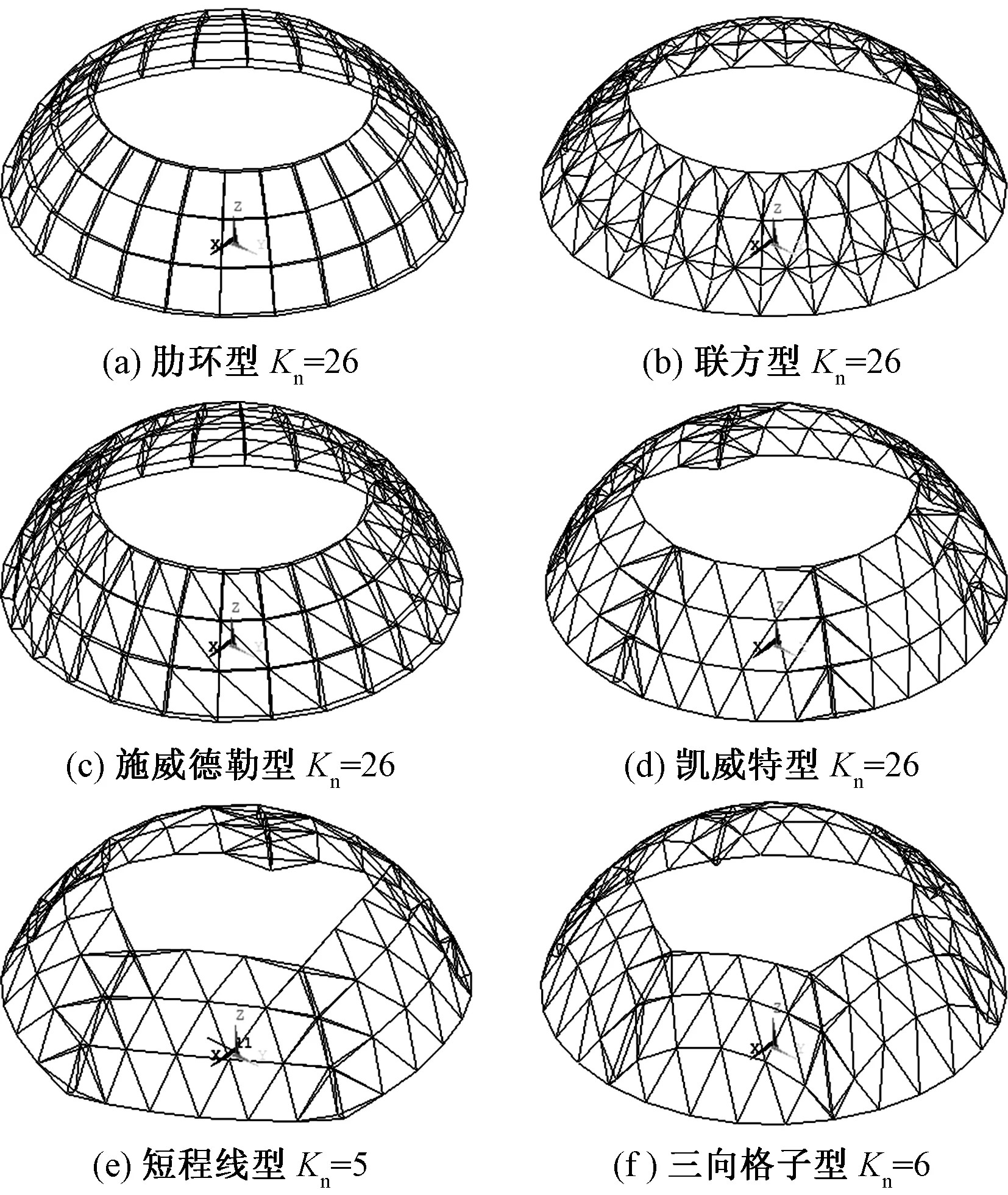
图3 6种局部双层去顶网壳模型
2 局部双层去顶网壳力学性能分析
由于三向格子型只能取Kn=6、短程线型只能取Kn=5,故根据空间网格结构技术规程[13],选取结构主要几何参数分别为S=120 m、f=45 m、T=2.5 m、Nx=6、Ns=3,短程线型选取Kn=5,凯威特与三向格子型均选取Kn=6,其余3种局部双层去顶网壳选取Kn=26。
结构外加q=2.35 kN/m2的均布载荷[14],考虑结构(杆件与节点)质量、支座形式选用固定铰支座,结构杆件采用截面积A=46.62 cm2的Q235钢管[13](直径d=219 mm、壁厚t=7 mm),钢材密度ρ=7 800 kg/m3,钢材弹性模量E=2.06×105MPa,结构许用位移为跨度的1/400[14],许用应力为[σ]=215 MPa。
图4和图5给出6种局部双层去顶球面网壳结构的位移、应力云图,表1给出计算分析数据。由图4、图5和表1可得如下结论。
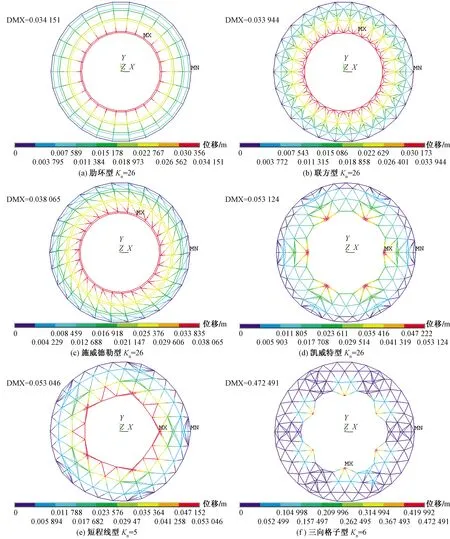
DMX表示结构最大位移;MX、MN分别表示最大位移、最小位移在结构中出现的位置
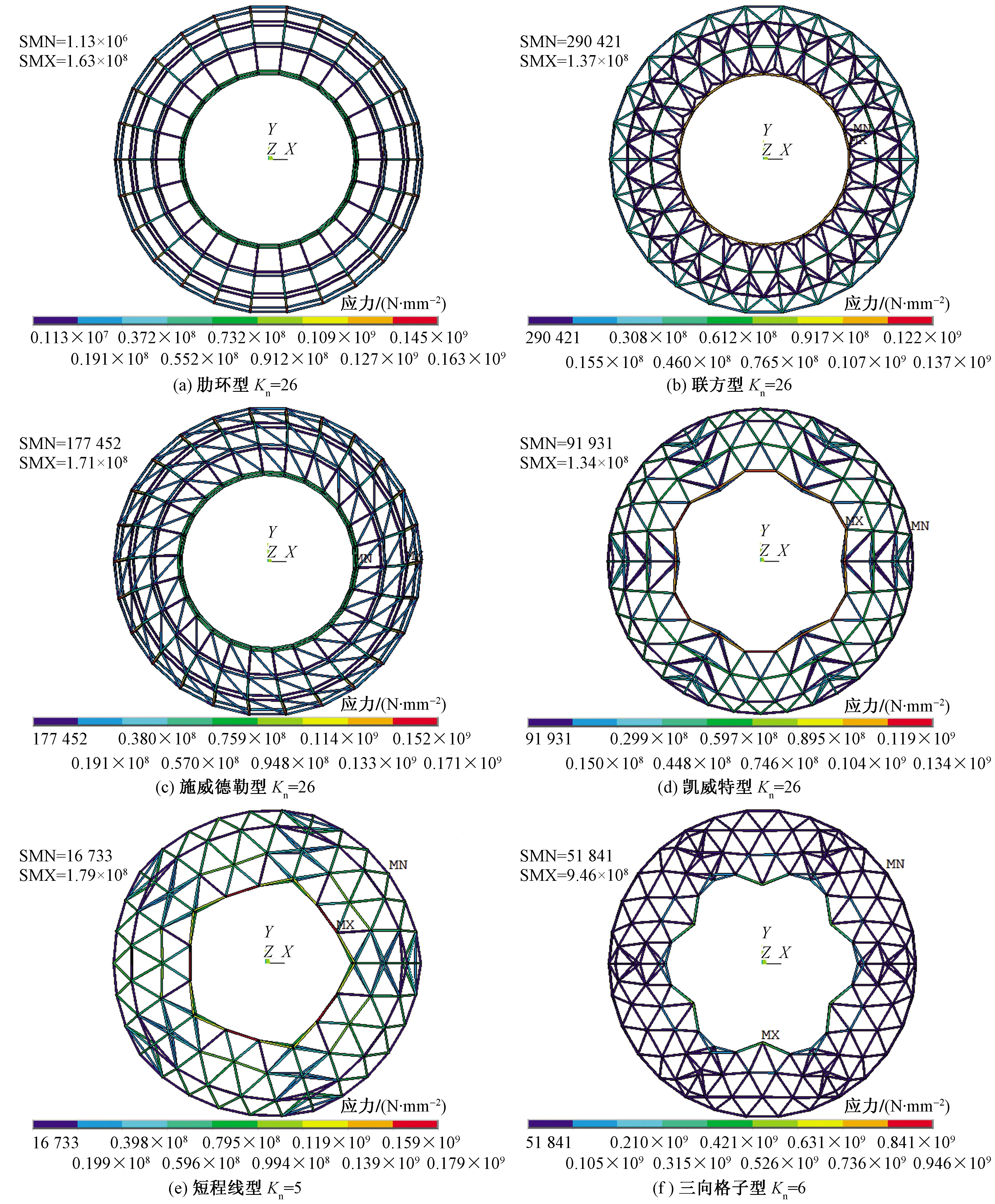
SMN、SMX分别表示结构最小应力与最大应力;MX、MN分别表示最大应力与最小应力在结构中出现的位置
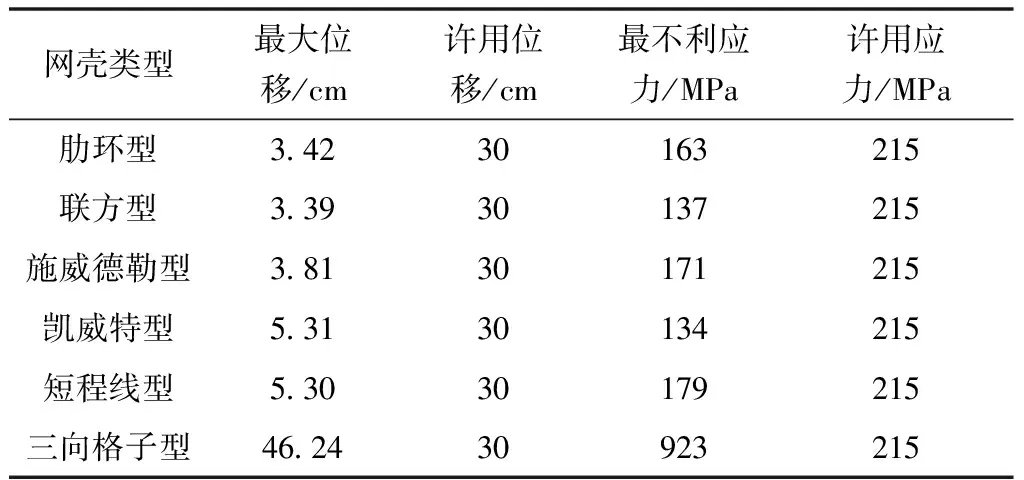
表1 最大位移与最大应力
(1)在均布载荷作用下、结构采用固定铰支撑,除肋环型和施威德勒型外,其余4类网壳结构最大位移和最大应力均出现在结构最顶圈;其中肋环型和施威德勒型最大位移和最大应力分别出现在结构最顶圈主肋节点处和第5圈主肋节点处;凯威特型最大位移和最大应力均出现在结构最顶圈主肋节点处;三向格子型的最大位移和最大应力均出现在结构最顶圈相邻主肋中间节点处;联方型网壳最大应力出现在结构最顶圈主肋节点处,最大位移出现在结构最顶圈三角锥节点处;短程线型网壳最大位移出现在结构最顶圈主肋节点处,最大应力出现在结构最顶圈主肋中间节点处。在结构设计和工程应用中可根据上述结构受力特点对结构进一步优化设计。
(2)在6类去顶结构中,凯威特型强度相对较高,结构应力最小;联方型最大位移最小,其最大应力与凯威特型接近,受力性能好于其余4种网壳结构,且远小于结构许用值,同等情况下具有较大的强度和刚度储备;三向格子型的最大位移与最大应力均大幅度超出了结构许用值,不适用于大跨度的露天型空间结构;其余3种结构力学性能相对接近,其节点与杆件的最大位移、最大应力均未超出结构许用值,可在实际工程中应用。
3 局部双层去顶球面网壳结构力学性能影响因素
3.1 T对结构力学性能的影响
由于T的取值范围为跨度的1/60~1/30[13],故S=120 m时,T取值为2~4 m。为研究T对局部双层去顶网壳力学性能的影响,现分别对T为2、2.5、3、3.5、4 m时相应的结构力学性能进行分析(其余结构几何参数及约束条件同第2节)。表2和表3给出计算分析数据。
由表2、表3分析如下。

表2 最大应力幅值

表3 最大位移
(1)当6类结构T的取值按照2、2.5、3、3.5、4 m 的顺序依次变化时,短程线型最大位移呈现先下降再增加最后减小的趋势,在T=2.5 m时位移幅值最小;其结构的最大应力则随着T的变大而逐渐下降,应力在T=4 m时取得最小值。由此可见,短程线型在T=2.5 m时有着较大的强度和刚度,且相较于T=4 m时的结构成本更小,在实际工程中短程线型结构厚度建议取2.5 m。
(2)三向格子型最大应力与最大位移均随T的加大而呈现先减小后增加的趋势,且均在T=2.5 m时取得最小值;之后由于厚度逐步加大,导致自重逐渐变大,从而迫使网壳力学性能降低。由于其最大应力与最大位移均超出结构许用值,故相同条件下不建议在大跨度去顶结构中应用。
(3)剩余4种网壳结构最大位移与最大应力均随着T的加大而逐渐降低,结构的强度、刚度储备随之增加,结构力学表现得到逐步改善。但结构随T的变化不大,即T对其余4种结构影响较小。在实际工程中考虑到成本等经济因素,4种结构在满足需求前提下可选择较小的厚度取值。
3.2 f对结构力学性能的影响
为探究矢高f对结构静力性能影响,现选取网壳矢高f=45~65 m(步长5),其余几何参数及约束条件不变(同第2节)。表4、表5给出计算分析数据。
由表4、表5分析如下。

表4 最大应力

表5 最大位移
(1)除三向格子型外其余5种类网壳结构节点与杆件的最大应力均因f的加大呈现先下降后上升的变化规律,且均在f=60 m时应力幅值最小;其中凯威特型在6种结构矢高同为60 m时最大应力最小,有着较大的强度储备;三向格子型的结构最大应力因f的加大呈现先升高后减小的规律,且远超出许用值,结构强度储备较差。
(2)在6种去顶网壳中,短程线型节点与杆件的最大位移随f的增大呈现先减小再增加最后减小的趋势,在f=50 m时最大位移取得最小值;三向格子型位移最值随f的加大呈现先上升后减小的态势,且均超出许用值,结构刚度储备较差;随f的取值逐渐增大,其余4种结构的最大位移均先降低后增高,在f=60 m时可得到最小值;当f=60 m时,联方型最大位移在6类结构中最小,其刚度最好。
(3)除短程线型外,其余5种结构的最大节点位移随f变化规律与相对应的最大应力变化规律相同,且除短程线与三向格子型外的4种结构均在f=60 m时力学性能最优,故而4种结构最优矢跨比为1/2;其中联方型在f=60 m时强度与凯威特型接近,且最大位移在6种结构中最小,综合受力性能较好,建议在工程中优先选用。
4 结论
通过研究6类局部双层去顶网壳杆件、节点的分布规律与连接方法,应用有限元计算软件的程序设计语句,研制了相应的模型设计程序,实现了给定相应去顶结构主要几何参数下的6类局部双层去顶网壳的参数化模型设计;并对6类网壳的力学性能进行了分析研究,通过对6种网壳位移幅值与应力幅值的分布、变化规律以及结构几何参数f、T对其力学性能影响规律的研究。现得出如下结论。
(1)根据6类局部双层去顶球面网壳结构的节点生成规律和杆件连接方法所设计的程序简单、高效、实用,为实际工程中此类结构的模型建立、力学性能分析和结构选型优化带来了极大便利。
(2)除肋环型和施威德勒型外,其余4种网壳的最大位移和最大应力均出现在网壳的最顶圈去顶部分;其中三向格子型的最大节点位移与最大应力均超出了结构允许值,故此类网壳不适用于大跨度空间结构;而联方型最不利应力和最大位移均较小、远小于结构许用值,受力性能在6类去顶结构中相对最好,建议在大跨度露天结构中优先选用。
(3)在跨度等结构几何参数与边界条件相同的情况下,6类局部双层去顶球面网壳可通过变换网壳厚度T和矢高f来改善结构受力性能。根据网壳的T和f对6种网壳结构力学性能影响规律及对结构造价成本的考量,建议此类结构在工程设计应用时应尽可能选取矢跨比为1/2和T的较小值。
