牙嵌式离合器的运动及失效分析①

许怡贤,王文中,黎 彪,王 波,从 强

(1.北京空间飞行器总体设计部,北京 100094;2.北京理工大学机械与车辆学院,北京 100081)

0 引言

在空间可展开结构中,为了提高展开的可靠性,通常会对展开的核心部件即驱动源进行备份[1-4]。当互为备份的两个驱动源有一个出现故障时,需要将其从传动链路中脱离出来,此时需要使用离合器来实现这个功能,同时,离合器也可以实现驱动源的过载保护。 离合器是一种实现主从动部件在同轴线上传递运动和动力,并具有接合与分离功能的装置[5-6]。 离合器有摩擦式离合器、液力变矩器(液力耦合器)、电磁离合器、牙嵌式离合器等,广泛应用在自动机械变速箱(AMT)中[7-9]。 其中,牙嵌式离合器传递转矩大,接合后主从动轴无相对滑动,传动比不 变, 适 用 于 转 速 差 较 小 时 接 合(≤ 150 r/min)[10-12],其体积可以设计到很小(Ф30×50 mm),构型简单可靠性高,非常适合在空间可机构中使用。 牙嵌离合器在不同工况下可以使用不同的牙形,包括矩形、正梯形、斜梯形、锯齿形、三角形和螺旋形等,其中,梯形牙使用最为广泛,其强度高,传递转矩大,分离时容易脱开,接合时冲击小,并可以消除牙侧间隙[13]。

Gergely 等人通过对牙嵌式离合器的运动学模型的建立,得出了不同初始速度差下离合器成功接合的概率,并且通过大量试验数据的统计评估进行了验证[14]。

Boka 等人对牙嵌式离合器的接合过程进行了研究,建立了变速箱制动-单面齿离合器系统的动力学模型,并通过给定AMT 的不同齿轮的数值模拟,提供了离合器最佳的接合条件[15]。

孙冬梅等人对正梯形牙嵌离合器的接合与分离过程进行了阶段划分,确定了决定顺利接合允许转速差所在的阶段。 分析了牙齿顺利接合的允许速差,研究了正梯形牙嵌离合器的保持接合与分离条件,并给出了计算公式[16]。

目前对牙嵌式离合器的研究为如何保证离合器顺利平稳接合,且目前离合器设计手册中关于离合器离合力矩的计算公式忽略了摩擦力对离合力矩的影响。 本文将推导考虑齿面摩擦及轴向运动摩擦的离合力矩计算公式,并对摩擦对离合器性能的影响进行分析,结合试验和微观形貌观测结果,指导牙嵌式离合器的设计、生产和使用,进一步提高其在空间可展开结构中使用的可靠性。

1 离合力矩分析的理论模型

在一个理论离合力矩为2.8 Nm 的梯形牙离合器的测试中,经过多次使用后,离合力矩下降到1.07 ~2.27 N·m。 平均值整体下降40%左右,并且测试得到的离合力矩离散型也显著增大,该离合器的构型和牙形如图1、图2 所示,其由弹簧、上离合器和下离合器组成。

图1 离合器的构型Fig.1 The configuration of the clutch

图2 离合器的牙形(梯形牙)Fig.2 The tooth shape of the clutch (trapezoidal tooth)

根据离合器工作原理,可以发现离合力矩主要与上下离合器的牙型半角、齿面粗糙度、活动半离合器与轴配合处的摩擦、活动离合器与下一级传动齿轮啮合处的摩擦相关。 取其中一个齿形进行受力分析,如图3 所示。

图3 啮合齿受力分析图Fig.3 Force analysis of meshing tooth

齿面的接触力FN和摩擦力Ff的合力为F。 合力F的水平分量与离合器的驱动力F驱相平衡,合力F的轴向分量与F轴向相平衡,表达式如下:

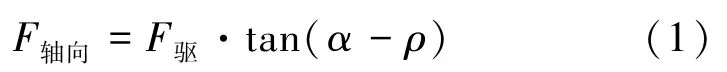
式(1)中α为梯形角度,ρ为当量摩擦角。

当量摩擦角ρ的计算表达式如下:

式(2)中μ为梯形牙摩擦系数。

离合器轴向方向的合力来源于三个方面,分别为弹簧作用力,轴孔摩擦力以及活动离合器与下一级传动齿轮啮合处的摩擦力,其表达式如下:

轴孔摩擦力以及活动离合器与下一级传动齿轮啮合处的摩擦力的近似计算表达式如下:

式(4)、式(5)中μ1为齿啮合处摩擦系数,μ2为离合轴径处摩擦系数,d为外啮合齿直径。

驱动力矩的表达式如下所示:

式(6)中Dp为梯形牙中径。

联立上述各式并整理化简,得到离合力矩TC的计算表达式如下:

其中,F弹为弹簧驱动力,α压为离合轮齿轮副的压力角。

由该理论公式可见,当弹簧力、齿型固定的情况下,离合力矩主要受到各个摩擦副摩擦系数的影响。

2 离合力矩的敏度分析

由上述分析可知,牙嵌离合器的结构固定后,离合力矩主要受离合齿之间、离合齿与轴之间的摩擦力影响,而随着摩擦表面状态的变化,离合器的性能也会出现变化,甚至造成离合器失效,以下对不同摩擦系数以及轴孔间隙对离合力矩的影响进行分析。

2.1 离合器的运动过程受力分析

离合器在分离过程中,齿间的啮合状态不断发生变化,啮合齿承受的接触压强也在不断发生变化。分别取三个典型位置即初始啮合位置、啮合行程一半的位置和退出啮合前的极限位置进行分析。

首先,对上下离合器进行网格划分。 选用六面体C3D8R 单元进行离散,单元总数为65 446 个。 其次将下离合器底部端面完全约束,上离合器侧端面coupling 到其质心参考点,该参考点施加绕z 轴转动位移边界条件,其他方向自由度不作约束。 弹簧力通过在弹簧作用区域施加均布压强的方式来施加。同时在上离合器中心建立柱坐标系,并在上离合器中心参考点上施加径向力,从而将离合器和下一级传动齿轮啮合产生的径向力作用考虑进来。 完成边界条件的施加后,通过提取上离合器中心参考点的反作用力矩即为离合驱动力矩,如图4、图5 所示。

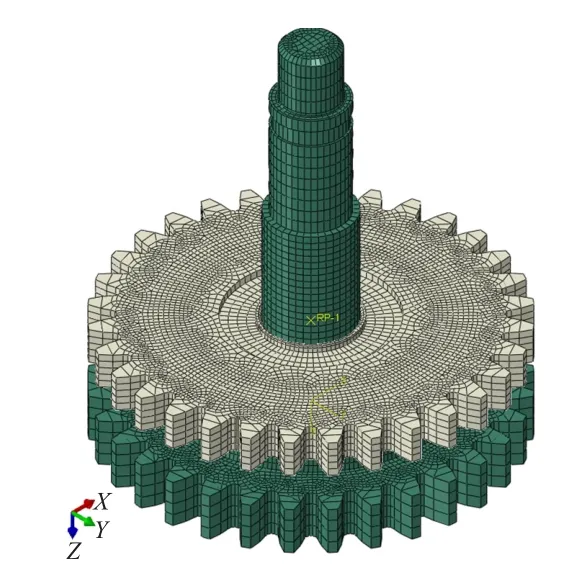
图4 离合器网格模型Fig.4 Finite element model of the clutch

图5 分析边界条件Fig.5 Analyze boundary conditions

图6 为各个啮合位置处的接触压强分布,由图6可知接触压强集中分布在大径方向。 从不同啮合位置的接触应力云图对比可以看出,随着离合器的转动分离,上下离合器啮合齿间的接触面积不断减小,接触压强不断增加。 不同啮合位置的接触压强总结如表 1 所列。 初始啮合位置的接触压强为78.6 MPa,随着离合器的转动达到齿顶与齿顶相互啮合的状态时,齿面接触压强达到1 562 MPa,相比与初始时刻齿面接触压强显著升高。 由于磨损率随着接触压强的增大而升高,因此仿真结果表明大径位置的磨损情况比中径和小径位置严重,齿顶位置的磨损比齿根位置要明显。

图6 不同啮合位置的接触应力分布(轴孔间隙为0,摩擦系数0.15)Fig.6 Contact stress distribution of different meshing positions (shaft hole clearance is 0, friction coefficient is 0.15)

表1 不同啮合位置的接触压强Tab.1 Contact pressure at different meshing positions

2.2 不同摩擦系数的影响

分析摩擦系数对离合驱动力力矩的影响时,暂且不考虑轴孔间隙的影响,并将间隙量设定为0。不同摩擦系数会导致上下离合器啮合齿面间的摩擦力以及下离合器的轴和上离合器内柱面摩擦力发生变化,从而导致整体结构受力状态发生变化,进而显著影响离合力矩。 摩擦系数对离合力矩的影响如图7 所示。

从图7 可以看出,随着齿面和上离合器轴孔配合面摩擦系数的增大,离合力矩显著增大。 不同摩擦系数下的离合力矩如表2 所列,当摩擦系数从0.1 变化到0.2 时,其离合力矩由2.09 Nm 增加到3.2 Nm,增长幅度达到53.1%。 该结果与理论模型取得良好的一致性。

图7 摩擦系数对离合力矩的影响(轴孔间隙为0)Fig.7 The influence of friction coefficient on clutch torque(shaft hole clearance is 0)

表2 不同摩擦系数下的离合力矩Tab.2 Clutch torque under different friction coefficients

2.3 不同轴孔间隙的影响

上下离合器的轴孔间隙也会对结构的受力产生影响。 轴孔间隙会导致活动离合器发生偏斜,整体结构的受力发生偏载。 上下离合器啮合齿间不再均匀承受离合力矩作用,同时轴孔之间也将发生局部点接触作用。

不同轴孔间隙下得到的结构接触压强分布如图8 所示。 由图8 可知,考虑轴孔间隙后结构的接触压强呈现非均匀分布的特性,承载区域啮合齿的接触压强明显高于其他区域啮合齿的接触压强。 并且随着轴孔间隙的加大,各啮合齿之间的偏载程度也随之增大,从而可能会导致不同位置啮合齿的磨损程度不一样。 不同轴孔间隙下啮合齿的最高接触压强总结如表3 所列。

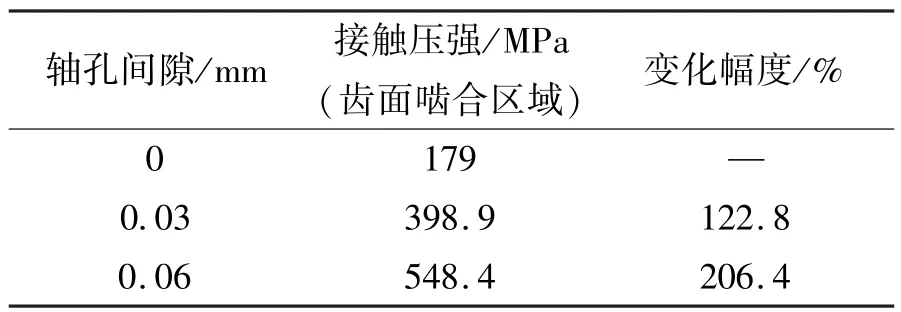
表3 不同轴孔间隙下啮合齿最大接触压强Tab.3 Maximum contact pressure of meshing teeth under different shaft hole clearances

不同轴孔间隙下转轴的接触压强分布如图9 所示。 由图9 可知,在考虑轴孔间隙之后,轴孔之间的接触压强分布形式由原来的均匀分布变为局部点接触。 随着轴孔间隙的加大,结构的偏载程度逐渐增大,轴孔之间的接触压强逐步升高。 不同轴孔间隙下轴孔之间的最高接触压强总结如表4 所列。

图9 不同轴孔间隙下轴孔接触压强分布Fig.9 Contact pressure distribution of shaft hole under different shaft hole clearance

如图10 所示为不同间隙下的离合力矩,不同间隙下离合力矩的大小和变化幅度总结如表5 所列。当轴孔间隙为0 时,离合力矩最终稳定在2.59 Nm。轴孔间隙为0.03 mm 的情况下得到的离合力矩达到2. 35 Nm,与0 间隙下的离合力矩相比降低9.2%。 进一步改变轴孔间隙至0.06 mm,其离合力矩的下降比例达到11.2%。 与摩擦系数对离合力矩的影响相比,轴孔间隙对离合力矩的影响并不显著,由此可知离合力矩的下降主要是由于啮合齿面磨损导致的摩擦系数下降所致。

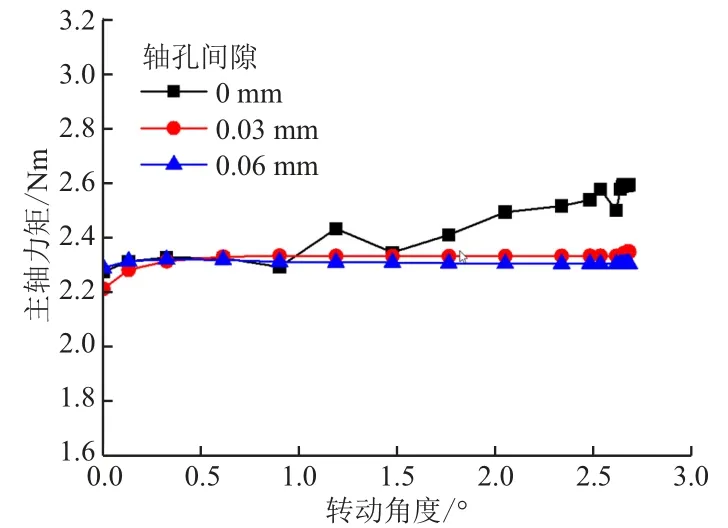
图10 间隙量对离合力矩的影响Fig.10 The effect of clearance on clutch torque

表5 不同轴孔间隙下的离合力矩Tab.5 Clutch torque under different shaft hole clearance

3 离合器的失效分析

对离合力矩下降的离合齿表面形貌以及轮廓进行观测发现,离合器大径位置处的表面粗糙高峰被磨平,表面粗糙度明显降低(下降了32%),而表面粗糙度的降低将会导致摩擦系数的明显降低[17],致使齿面所承受摩擦力降低。 即齿面的磨损导致了离合力矩的减小。

对离合轮齿和离合轮轴的配合表面形貌以及轮廓进行观测,轴孔的表面形貌并未体现出明显的磨损,轴孔的表面粗糙度变化也不大(平均值下降了1.6%),磨损前后对齿的运动影响变化不大,如图11 所示。

图11 显微镜拍摄磨损后受力面与新加工齿面Fig.11 Microscope photographs of the stressed surface and newly processed tooth surface after wear

由上述分析可知,离合力矩的下降主要是由离合齿面磨损造成的,这与理论分析结果基本相同。

4 结论

通过上述理论、仿真分析和齿面形貌观测可知:

1)有限元分析与试验观察结果均表明在齿面大径位置处接触压强较高,磨损现象较为严重;

2)存在轴孔间隙的情况下,上下离合器的最大接触压强显著增大,0.06 mm 轴孔间隙下的啮合齿最大接触压强比无间隙下的齿间最大接触压强增大206%;

3)离合器大径位置处的粗糙高峰被磨平,且齿顶磨损更为严重。 大径位置表面粗糙度的平均值降低达32%左右,而轴孔表面粗糙度幅值无明显变化。 由此推断齿面的磨损和摩擦系数下降是离合力矩下降的主要原因。

由于重量和包络尺寸的限制,空间可展开结构用牙嵌式离合器的尺寸通常会做的比较小,导致单个压的接触强度较低,抗摩擦能力较弱,在后续牙嵌式离合器设计时,应提高齿面的硬度以提高齿面的接触疲劳的强度,并加长离合器的导向距离,降低轴孔配合处的接触压强,提高牙嵌式离合器的可靠性。